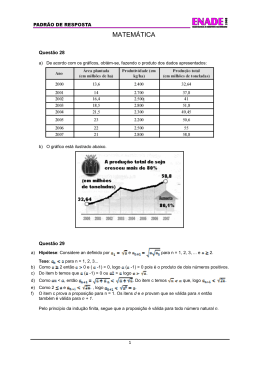
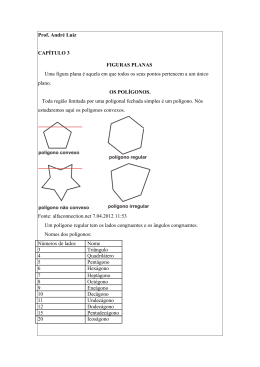
Versão do Teorema de Morley
para Paralelogramos
"One of the most surprising theorems in elementary geometry was
discovered about 1899 by R Morley. He mentioned it to his friends, who
spread it over the world in the form of mathematical gossip."
H.S.M.Coxeter
Consideremos u m t r i â n g u l o qualquer e as bissectrizes dos seus â n g u l o s internos. Se construirmos os pontos de
intersecção das bissectrizes adjacentes, e n t ã o obteremos sempre os vértices de u m t r i â n g u l o equilátero,
independentemente do t r i â n g u l o inicial que considerarmos. Este é o Teorema de Morley. Para mais informações
sobre este teorema, pode consultar a p á g i n a http://www.atractor.pt/mat/morley/.
Neste artigo, veremos o que acontece se considerarmos paralelogramos e m vez de t r i â n g u l o s . Construindo
da mesma forma as intersecções das trissectrizes adjacentes dos â n g u l o s internos de u m q u a d r i l á t e r o , e n t ã o
obteremos quatro pontos. U n i n d o estes pontos consecutivamente, p o d e m acontecer v á r i a s situações. Os pontos
p o d e m ser colineares o u p o d e m formar u m p o l í g o n o n ã o convexo, mesmo quando o q u a d r i l á t e r o inicial é
convexo, como se pode ver nas seguintes figuras:
Caderno_2_AF
ter
a-feira, 5 d e A g o s t o d e 2008 1 2 : 2 0 : 2 3
[Versão do Teorema de Morley para Paralelogramos]
N o entanto, se consideramos apenas paralelogramos, e n t ã o s ó p o d e m ocorrer duas situações: o u os quatro
pontos s ã o colineares o u s ã o vértices de u m outro paralelogramo. A l é m disso, se partirmos de u m r e c t â n g u l o ,
obteremos sempre u m losango, e, se partirmos de u m losango, obteremos sempre u m r e c t â n g u l o . Segue-se u m a
prova destes factos, supondo à partida que os quatro pontos de intersecção das trissectrizes n ã o são colineares.
1
Construa o paralelogramo [ABCD], as suas trissectrizes e os pontos de intersecção das trissectrizes
adjacentes, E,F,Ge H. U n a estes pontos consecutivamente, de m o d o a formar u m q u a d r i l á t e r o . C o m o AÒE =
CBG,DAE
= B C G eAD = BC, temos que os t r i â n g u l o s [ADE] e[CBG] s ã o congruentes, logo AE= CG e
DE=BG.
Analogamente, como ABF = CDH,
BAF = DCH
e Aty= CD, temos que os t r i â n g u l o s [ABF]e[CDH]
t a m b é m são congruentes, logo AF=CH
eBF = DH . C o m o E ^ i F = GCH,AE=CG
e AF=CH, temos que os
t r i â n g u l o s [EAF] e [GCH] s ã o congruentes, logo EF = GH. Analogamente, como
FBG = HDE,
BF = DH e
BG = DE, temos que os t r i â n g u l o s [FBG] e [HDE] t a m b é m s ã o congruentes, logo FG = HE . Portanto, o
q u a d r i l á t e r o [EFGH] é u m paralelogramo.
Demonstra-se que tal acontece quando a + b =
2
2
sin V? onde a e b são as medidas dos lados do paralelogramo e a é a medida de um dos seus ângulos internos. Em
71
V3 V3
particular, quandotemosum losango fgu seja, quando a = b) os pontos nunca são colineares e quandotemosum rectângulo (ou seja, quando cc= n 12) os pontos são
colineares quando ÇL
22|
Caderno_2_AF
ter
a-feira, 5 d e A g o s t o d e 2008 12:20:27
*"
Sa
[Versão do Teorema de Morley para Paralelogramos]
c
e
Se |y4BCD] é u m r e c t â n g u l o , e n t ã o todos os seus â n g u l o s internos s ã o rectos, pelo que s ã o trissectados e m
â n g u l o s de 30°. Temos e n t ã o que [AED], [AFB], [BGC] e [CHD] são t r i â n g u l o s isósceles, pelo que DE = AE= BG =
C G (são lados de 2 t r i â n g u l o s isósceles congruentes) e AF = BF = CH = DH (são t a m b é m lados de 2 t r i â n g u l o s
isósceles congruentes). Logo, como EAF = FBG , AF = BF e AE=BG
,temos que [EAF] e [FBG] s ã o
congruentes, pelo que FE = FG. C o m o [EAF] é congruente c o m [GCH], v e m FE = HG e, como [FBG] é
congruente c o m [HDE], v e m FG = HE . Portanto, os lados do paralelogramo [EFGH] s ã o todos iguais, o u seja,
[EFGH] é u m losango.
A
Caderno_2_AF
ter
a-feira, 5 d e A g o s t o d e 2008 12:20:29
D
[Versão do Teorema de Morley para Paralelogramos]
Se [ABCD] é u m losango, e n t ã o AD= ABe, como DÁE = FÂB e ADE = AÈF, temos que [ADE] e [ABF] s ã o
congruentes, logo AE = AF . C o m o [.ADE] é congruente c o m [CBG], temos que [ABF] e [CBG] t a m b é m s ã o
congruentes, logo BF = BG- Portanto, os t r i â n g u l o s [EAF] e [FBG] são isósceles e, consequentemente, t a m b é m os
t r i â n g u l o s [GCH]e[HDE]
s ã o isósceles, dado que estes s ã o congruentes com os anteriores. Temos e n t ã o que
AÈD = ÀpB = BGC = CÈD
(são â n g u l o s d e 4 t r i â n g u l o s congruentes),
AÇF = AFE = CGH = CHG
(são â n g u l o s de 2 t r i â n g u l o s isósceles congruentes) e BFG = BGF = DHE = DEH(são
t a m b é m â n g u l o s de 2
t r i â n g u l o s isósceles congruentes). Logo, os â n g u l o s internos do paralelogramo [EFGH] s ã o iguais, dado que as
suas amplitudes p o d e m ser obtidas subtraindo a 360° amplitudes de â n g u l o s iguais (por exemplo,
E F G = 3 6 0 ° - A F E - AFB- BFG = 360° - CGH - CGB- BGF = F GH). A l é m disso, a soma dos â n g u l o s internos
de qualquer q u a d r i l á t e r o é de 360°, logo todos os â n g u l o s internos do paralelogramo [EFGH] s ã o rectos, o u seja,
[EFGH]
é u m rectângulo.
Obviamente, se juntarmos as duas h i p ó t e s e s (todos os â n g u l o s de [ABCD] s ã o rectos e todos os seus lados s ã o
iguais), isso significa que [ABCD] é u m quadrado, pelo que, neste caso, conclui-se que [EFGH] t a m b é m o é. M a i s
geralmente, partindo de u m p o l í g o n o regular de n lados, se construirmos os pontos de intersecção das suas
trissectrizes adjacentes, e n t ã o obteremos sempre os vértices de outro p o l í g o n o regular de n lados.
Finalmente, ainda em relação ao caso geral dos paralelogramos, note-se que, em vez de escolher os pontos de
intersecção das trissectrizes adjacentes, p o d e r í a m o s ter escolhido os pontos de intersecção das trissectrizes n ã o
adjacentes de vértices consecutivos. T a m b é m aqui podemos concluir que estes pontos o u s ã o colineares o u s ã o
os vértices de u m outro paralelogramo, que é u m losango no caso do paralelogramo inicial ser u m r e c t â n g u l o e
vice-versa, sendo que a d e m o n s t r a ç ã o seria a n á l o g a à anterior. N a figura abaixo, temos representados estes dois
paralelogramos, sendo que o primeiro, obtido pela intersecção das trissectrizes adjacentes, encontra-se a
amarelo e o segundo encontra-se a cinzento. EH
241
Caderno_2_AF
ter
a-feira, 5 d e A g o s t o d e 2008 1 2 : 2 0 : 3 3