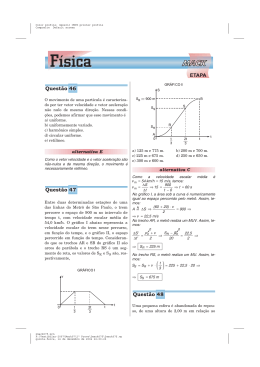
Color profile: Generic CMYK printer profile
Composite Default screen
TIPO DE PROVA: A
Questão 3
Questão 1
⎛ 2 −1⎞
Se A 3 = ⎜
⎟ , o triplo do determinante
⎝ −4 6 ⎠
Qualquer que seja x não nulo, tal que| x| ≠ 1,
x+1
x −1
−
x
1
x+1
−
a expressão
1
1
+
x+1
x −1
é sempre igual a
1
b) 2x
c) x + 2
d) 1
e) 2
a)
x
da matriz A é igual a
a) 3
b) 6
c) 9
d) 12
e) 15
alternativa B
3
Temos det(A ) = 2 ⋅ 6 − (−4) ⋅ (−1) = 8 ⇔
⇔ (det A) 3 = 8 ⇔ det A = 2.
Logo o triplo do determinante da matriz A é 3 ⋅ 2 = 6.
alternativa E
Questão 4
Considerando x ≠ 0 e | x | ≠ 1, temos
2
(x + 1) − (x − 1)
x +1
x −1
−
(x − 1)(x + 1)
x −1
x +1 =
1
1
x −1 + x +1
+
(x + 1)(x − 1)
x +1
x −1
=
2
=
O retângulo assinalado na figura possui área
máxima. Essa área é igual a
(x + 1 + x − 1)(x + 1 − x + 1)
4x
=
= 2.
2x
2x
Questão 2
x
1
será igual a
, se o numerador
y
2
for aumentado de 2 unidades e o denominador aumentado de 1 unidade; entretanto, se o
numerador for aumentado de 1 unidade e o
denominador diminuído de 2 unidades, a fra3
ção ficará igual a . Dessa forma, x y é igual
5
a
a) 32
b) 64
c) 128
d) 81
e) 121
A fração
alternativa C
Admitindo y ≠ −1 e y ≠ 2 , temos:
x +2
1
=
y +1
2
2x − y = −3
⇔
⇔ x =2ey =7
x +1
3
5x − 3y = −11
=
y −2
5
Assim, x y = 27 = 128 .
1mack07m.prn
F:\Vestibular-2007\Mack07\1“ Prova\1mack07m\1mack07m.vp
quarta-feira, 13 de dezembro de 2006 23:19:48
a) 12
b) 10
c) 15
d) 8
e) 14
alternativa A
Sejam x e y as dimensões do retângulo, conforme
desenho a seguir.
Color profile: Generic CMYK printer profile
Composite Default screen
matemática 2
Da semelhança de triângulos concluímos que
6 −y
6
3
=
⇔ y = − x + 6.
x
8
4
⎛ 3
⎞
A área do retângulo é A(x) = x ⎜ − x + 6 ⎟ =
⎝ 4
⎠
3 2
= − x + 6x . Essa função quadrática tem valor
4
Δ
62
máximo dado por −
= 12 .
=−
4a
⎛ 3⎞
4 ⋅ ⎜− ⎟
⎝ 4⎠
Portanto, a área máxima do retângulo é 12.
Questão 6
Em relação a um sistema cartesiano ortogonal, com os eixos graduados em quilômetros, uma lancha sai do ponto (−6, −4), navega 7 km para leste, 6 km para o norte e 3 km
para oeste, encontrando um porto. Depois
continua a navegação, indo 3 km para norte e
4 km para leste, encontrando um outro porto.
A distância, em quilômetros, entre os portos é
a) 7
b) 3 5
c) 2 3
d) 7
e) 5
Questão 5
alternativa E
Os gráficos de y = x + 2 e x + y = 6 definem,
com os eixos, no primeiro quadrante, um quadrilátero de área
a) 12
b) 16
c) 10
d) 8
e) 14
alternativa E
Representando os gráficos de y = x + 2 e
x + y = 6 num mesmo sistema de eixos, temos:
O percurso da lancha pode ser representado por
(−6; −4)
7 km leste
(−6 + 7; −4) = (1; −4)
6 km norte
3 km oeste
7 km norte
4 km leste
(1; −4 + 6) = (1; 2)
= (−2; 2) (porto 1)
(−2; 2 + 3) = (−2; 5)
= (2; 5)(porto 2).
6 km norte
(1 − 3; 2) =
(−2 + 4; 5) =
A distância, em quilômetros, entre os portos é:
(2 − ( −2)) 2 + (5 − 2) 2 = 5.
Questão 7
A figura mostra os esboços dos gráficos das
funções f(x) = 22x e g(x) = log2 (x + 1). A área do
triângulo ABC é
O ponto P é a
y =x +2
x =2
⇔
x + y =6
y =4
solução
do
sistema:
Assim, a área do quadrilátero definido no 1º quadrante com os eixos é igual à soma da área do
quadrilátero formado pelos pontos P = (2; 4),
R = (2; 0), O = (0; 0) e S = (0; 2) com a área do
triângulo formado pelos pontos R = (2; 0),
P = (2; 4) e Q = (6; 0). Logo:
(4 + 2)2
área do quadrilátero OSPQ =
+
2
4 ⋅4
+
= 14
2
1mack07m.prn
F:\Vestibular-2007\Mack07\1“ Prova\1mack07m\1mack07m.vp
quarta-feira, 13 de dezembro de 2006 23:19:49
a)
1
4
b)
5
2
c)
3
2
d)
2
5
e)
1
3
Color profile: Generic CMYK printer profile
Composite Default screen
matemática 3
alternativa C
Sejam os pontos A (x A ; y A ), B (xB ; y B ) e
C (xC ; yC ) vértices do triângulo em questão.
Pelo gráfico, supondo que AB é paralelo ao eixo
Ox, temos xB = 0 e y B = f(xB ) = 2 2 ⋅ 0 = 1;
y A = y B = 1 e y A = g(x A ) = 1 ⇔
⇔ log 2 (x A + 1) = 1 ⇔ x A = 1;
xC = x A = 1 e yC = f(xC ) = 2 2 ⋅1 = 4.
Assim, os possíveis números são 41, 43 e 47, cujas somas dos algarismos são 5, 7 e 11, respectivamente. Portanto a soma dos algarismos pode
ser 7.
Questão 10
Assim os vértices são A (1; 1), B (0; 1) e C (1; 4),
AB = x A − xB = 1, AC = yC − y A = 4 − 1 = 3 e
AB ⋅ AC
1 ⋅3
3
a área do ΔABC é
.
=
=
2
2
2
Questão 8
Se a, b e c são as raízes da equação
1
1
1
x 3 − 2x2 + 3x − 4 = 0, então
+
+ vale
a
b
c
2
4
7
3
1
a)
b)
c)
d)
e)
3
3
3
4
4
alternativa D
1
1
1
bc + ac + ab
.
+
+
=
a
b
c
abc
Sendo a, b e c as raízes da equação
x 3 − 2x 2 + 3x − 4 = 0, pelas relações entre coeficientes e raízes temos bc + ac + ab = 3 e
bc + ac + ab
3
.
abc = 4, assim
=
abc
4
Questão 9
Um número primo e positivo é formado por 2
algarismos não nulos. Se, entre esses algarismos, colocarmos um zero, o número ficará aumentado em 360 unidades. Dessa forma, a
soma desses 2 algarismos pode ser
a) 8
b) 7
c) 6
d) 9
e) 10
alternativa B
Dois paralelepípedos retângulos de mesmas
dimensões cortam-se conforme a figura, sendo igual a 1 o volume da região assinalada.
Se ABCD é um quadrado, e o volume total do
sólido obtido, incluindo a região assinalada, é
9, a dimensão b é igual a
a) 2
b) 6
c) 5
d) 3
e) 4
alternativa C
A região assinalada é um cubo de aresta a, logo
a3 = 1 ⇔ a = 1.
Os dois outros sólidos são paralelepípedos retângulos cujas bases são quadrados de lado a e cuja
altura é b − 1.
Como o volume total do sólido é 9, podemos afirmar que:
2 ⋅ 12 ⋅ (b − 1) + 13 = 9 ⇔ b = 5 .
Questão 11
Um ambulante paga R$ 1,00 pela compra
de 3 lápis e revende por R$ 2,00 cada 5 lápis. A quantidade necessária de lápis que
deve ser vendida, para que ele tenha um lucro de R$ 50,00 é
a) 600
b) 750
c) 550
d) 440
e) 620
O número primo positivo formado por 2 algarisalternativa B
mos não-nulos pode ser representado por
(ab) = a ⋅ 10 + b (a ≠ 0 e b ≠ 0). Ao colocar um Na compra de 15 lápis, o ambulante paga
zero entre a e b obtém-se o número 5 ⋅ R$ 1,00 = R$ 5,00 e os revende por 3 ⋅ R$ 2,00 =
= R$ 6,00. Assim, o lucro obtido na compra de 15
(a0b) = a ⋅ 100 + 0 ⋅ 10 + b.
Como a diferença entre os dois números obtidos lápis é R$ 6,00 − R$ 5,00 = R$ 1,00. Logo para
é 360, então a ⋅ 100 + 0 ⋅ 10 + b − a ⋅ 10 − b = que o lucro seja de R$ 50,00 é necessário vender
= 360 ⇔ 90a = 360 ⇔ a = 4.
15 ⋅ 50 = 750 lápis.
1mack07m.prn
F:\Vestibular-2007\Mack07\1“ Prova\1mack07m\1mack07m.vp
quarta-feira, 13 de dezembro de 2006 23:19:51
Color profile: Generic CMYK printer profile
Composite Default screen
matemática 4
alternativa A
Questão 12
Na figura, a reta t é tangente à circunferência de centro O e raio 2 . A área do triângulo ABC é igual a:
O total de maneiras distintas de um casal ter 4 filhos é 2 ⋅ 2 ⋅ 2 ⋅ 2 = 2 4 = 16 e o número de maneiras de ter 2 meninos (e conseqüentemente 2
⎛4 ⎞
4 ⋅3
meninas) é ⎜ ⎟ =
= 6.
⎝2 ⎠
2
6
3
Logo a probabilidade pedida é
= .
16
8
Questão 14
Observe a disposição, abaixo, da seqüência
dos números naturais ímpares.
1ª linha → 1
2ª linha → 3,5
3ª linha → 7,9,11
4ª linha → 13,15,17,19
5ª linha → 21,23,25,27,29
...........
..........................
O quarto termo da vigésima linha é
a) 395
b) 371
c) 387
d) 401
e) 399
a)
4 2
3
b)
3 2
2
d)
3 3
2
e)
5 2
3
c)
5 3
3
alternativa D
Na figura dada, temos AO = OB = 2 . O triângu$
lo OBC é retângulo em B; como m (OCB)
= 30o ,
o
$
temos m (COB)
= 60 . Assim, OC = 2 ⋅OB = 2 2 .
$
Temos, também, m (AOB)
= 180o − 60o = 120o .
Logo:
área ΔABC = área ΔAOB + área ΔBOC =
2 ⋅ 2 ⋅ sen120o
2 ⋅ 2 2 ⋅ sen 60o
+
=
2
2
3
3
3 3
.
=
+2 ⋅
=
2
2
2
=
Questão 13
Um casal planeja ter 4 filhos; admitindo probabilidades iguais para ambos os sexos, a
probabilidade de esse casal ter 2 meninos e 2
meninas, em qualquer ordem, é:
3
3
1
1
3
a)
b)
c)
d)
e)
8
4
2
16
16
1mack07m.prn
F:\Vestibular-2007\Mack07\1“ Prova\1mack07m\1mack07m.vp
quarta-feira, 13 de dezembro de 2006 23:19:52
alternativa C
Observando a disposição dos números, na n-ésima linha temos n números. Logo até a 19ª linha
temos:
(1 + 19) ⋅ 19
1 + 2 + 3 + ... + 19 =
= 190 números.
2
Assim o 4º número da vigésima linha é o 194º número natural ímpar, igual a 1 + (194 − 1) ⋅ 2 = 387.
Questão 15
Com relação à reta que passa pela origem e é
tangente à curva ( x − 3)2 + ( y − 4 )2 = 25,
considere as afirmações:
I. é paralela à reta 3x − 4y = 25.
II. é paralela à bissetriz dos quadrantes pares.
III. é perpendicular à reta 4x − 3y = 0.
Dessa forma,
a) somente I está correta.
b) somente II está correta.
c) somente III está correta.
d) somente I e III estão corretas.
e) I, II e III estão incorretas.
Color profile: Generic CMYK printer profile
Composite Default screen
matemática 5
alternativa C
Como (0 − 3) 2 + (0 − 4) 2 = 25 , concluímos que
a circunferência de equação (x − 3) 2 + (y − 4) 2 =
= 25 passa pela origem. A reta que passa pela
origem e pelo centro (3; 4) da circunferência tem
4
coeficiente angular
. Logo a reta que passa
3
pela origem e é tangente à circunferência tem
1
3
coeficiente angular − 4 = − .
4
3
I. Incorreta, pois o coeficiente angular da reta
3
3
3
25
é
3x − 4y = 25 ⇔ y =
≠− .
x −
4
4
4
4
II. Incorreta, pois o coeficiente angular da bissetriz
3
dos quadrantes pares é tg135 o = −1 ≠ − .
4
III. Correta, pois o coeficiente angular da reta
4 4 ⎛ 3⎞
4
4x − 3y = 0 ⇔ y =
xé e
⋅ ⎜ − ⎟ = −1.
3 3 ⎝ 4⎠
3
⎛6 − 2 ⎞ ⎛ 4 ⎞
⎛4 − 2 ⎞ ⎛2 ⎞
quarto, ⎜
⎟ = ⎜ ⎟ , e do último, ⎜
⎟ = ⎜ ⎟.
⎝ 2 ⎠ ⎝2 ⎠
⎝ 2 ⎠ ⎝2 ⎠
Logo o número de maneiras diferentes de apresentar os 10 algarismos na tela é:
⎛10 ⎞ ⎛8 ⎞ ⎛ 6 ⎞ ⎛ 4 ⎞ ⎛ 2 ⎞
⎜ ⎟ ⋅⎜ ⎟ ⋅⎜ ⎟ ⋅⎜ ⎟ ⋅⎜ ⎟ =
⎝ 2 ⎠ ⎝2 ⎠ ⎝2 ⎠ ⎝2 ⎠ ⎝2 ⎠
=
10 ⋅ 9 8 ⋅ 7 6 ⋅ 5 4 ⋅ 3 2 ⋅ 1 10!
⋅
⋅
⋅
⋅
= 5 .
2
2
2
2
2
2
Questão 17
π
π
π
cotg ⎛⎜ +
+
+ . . .⎞⎟ é igual a
⎝3
⎠
6
12
3
3
a) 3 b) − 3 c)
d) −
3
3
e) 2
3
3
alternativa D
Questão 16
Ao utilizar o caixa eletrônico de um banco, o
usuário digita sua senha numérica em uma
tela como mostra a figura. Os dez algarismos
(0,1,2,3,4,5,6,7,8,9) são associados aleatoriamente a cinco botões, de modo que a cada botão correspondam dois algarismos, indicados
em ordem crescente. O número de maneiras
diferentes de apresentar os dez algarismos
na tela é
10!
10!
c) 25 ⋅ 5!
a) 5
b)
5
2
10!
d) 25 ⋅ 10!
e)
2
⎛π π π
⎞
A seqüência ⎜ , ,
, ...⎟ é uma progressão
⎝ 3 6 12
⎠
π
geométrica infinita de primeiro termo
e razão
3
π
6 = 1 . Assim, cotg ⎛⎜ π + π + π + ...⎞⎟ =
⎝3
⎠
π
6
12
2
3
⎛ π ⎞
⎜
⎟
π
2π
= cotg ⎜ 3 ⎟ = cotg
= − cotg
=
1
3
3
⎜1 −
⎟
⎝
2 ⎠
3
π
.
= −tg
=−
6
3
Questão 18
1
3
log m5 −
log m = log 3 , m > 0, o va4
4
lor de m é
a) 4
b) 3
c) 2
d) 1
e) 10
Se
alternativa B
alternativa A
O número de maneiras de apresentar os alga⎛10 ⎞
rismos do primeiro botão é ⎜ ⎟ , do segundo,
⎝2 ⎠
⎛10 − 2 ⎞
⎛8 − 2 ⎞
⎛8 ⎞
⎛6 ⎞
⎜
⎟ = ⎜ ⎟ , do terceiro, ⎜
⎟ = ⎜ ⎟ , do
⎝ 2 ⎠
⎝ 2 ⎠
⎝2 ⎠
⎝2 ⎠
1mack07m.prn
F:\Vestibular-2007\Mack07\1“ Prova\1mack07m\1mack07m.vp
quarta-feira, 13 de dezembro de 2006 23:19:54
Para m > 0, temos
1
3
log m5 − log m = log 3 ⇔
4
4
1
3
5
log m = log 3 2 ⇔
log m −
4
4
1
1
log m =
log 3 ⇔ m = 3.
⇔
2
2
⇔
Color profile: Generic CMYK printer profile
Composite Default screen
matemática 6
Questão 19
Questão 20
Supondo que, neste Processo Seletivo 2007, a
relação candidato/vaga seja 5,5, e que, para
2008, haja um aumento de 18% no número de
candidatos e um aumento de 10% no número
de vagas oferecidas, a relação candidato/vaga
para 2008 será de
a) 5,9
b) 5,4
c) 5,7
d) 6
e) 6,1
A soma das soluções inteiras da inequação
1 1 1
1 x 3 ≥ 0é
alternativa A
c
= 5,5 .
v
Como para 2008 o número de candidatos será
18
c +
c = 1,18c e o número de vagas
100
10
v +
v = 1,1v , a relação candidato/vaga será
100
1,18c
1,18
=
⋅ 5,5 = 5,9.
1,1v
1,1
No processo seletivo de 2007 temos
1mack07m.prn
F:\Vestibular-2007\Mack07\1“ Prova\1mack07m\1mack07m.vp
quarta-feira, 13 de dezembro de 2006 23:19:55
1 x2 9
a) 0
b) 2
c) 5
d) 6
e) 7
alternativa D
1 1 1
1 x 3 ≥ 0 ⇔ (x − 1)(3 − 1)(3 − x) ≥ 0 ⇔
1 x2 9
⇔ (x − 1)(x − 3) ≤ 0 ⇔ 1 ≤ x ≤ 3.
Logo a soma das soluções inteiras da inequação
dada é1 + 2 + 3 = 6.