CAPÍTULO 6 - ESTRUTURA DE SELEÇÃO
6.1 - INTRODUÇÃO
Existem problemas que podem ter mais de um caminho a ser seguido para seleção
correta, ou existem restrições em suas soluções.
O sujeito que irá executar o algoritmo, em dado momento, deve então tomar a decisão
do caminho que deverá seguir para chegar à solução correta do problema.
Esta decisão, do caminho a ser seguido, tem de estar fundamentada em alguma lógica.
E é função de quem escreve o algoritmo, dar condições para o sujeito que o executa, fazer a
escolha correta do caminho para se chegar à solução do problema.
Um exemplo simples de problema que pode ter metodologias diferentes em sua
solução, são os cálculos das raízes de equações polinomiais do 2°. grau (ax2 + bx + c = 0). Se
o termo b2 - 4ac for maior ou igual a zero, as raízes serão reais, caso contrário, serão
complexas.
Não seria correto nós escrevermos um algoritmo que resolvesse somente a parte de
raízes reais, ou, a parte complexa, pois a metodologia que vai ser usada somente será
conhecida em tempo de execução do algoritmo. Logo, temos que descrever a solução por
ambas as metodologias, mas deixando claro para o sujeito que vai executá-la, que ele terá de
fazer uma escolha entre os caminhos possíveis.
Mas se deixássemos a critério de quem executa o algoritmo, será que ele sempre
escolheria o caminho correto?
Pelo sim, pelo não, não podemos arriscar. Por isso, é que, além de dizermos que existe
mais de um caminho para a solução do problema, ainda temos de prover subsídios para que o
mesmo faça a escolha do caminho correto.
Assim, o simples fato de nós informarmos que a solução do problema tem duas ou
mais metodologias diferentes em sua solução, não funcionam. Temos ainda, que dizer em
quais situações ele utilizará a metodologia A, e em que outras ele utilizará a B.
No caso das raízes de polinômio do 2°. grau, poderíamos utilizar a seguinte descrição
narrativa:
se o resultado de b2 - 4ac for maior ou igual a zero,
então utilize a metodologia de cálculo de raízes reais,
senão utilize a metodologia de cálculo de raízes complexas.
6.2 - ESTRUTURA SE ENTÃO
A estrutura se então permite determinar se um certo conjunto de instruções de um
algoritmo deve ou não ser executada.
A sintaxe geral (ver figura 6.1) desta instrução é:
se condição
então
inst1;
inst2;
inst3;
….....
instN;
bloco de instruções
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
onde:
61
se então é a instrução de seleção.
condição pode ser um identificador do tipo lógico, ou uma expressão
relacional, ou uma expressão lógica.
instl; ...; instN formam o conjunto de instruções que serão ou não
executadas.
F
se condição
V
inst_1;
inst_2;
......;
inst_N;
Figura 6.1 Estrutura SE ENTÃO
A semântica desta instrução é:
O termo condição de instrução somente poderá produzir o valor falso ou verdadeiro.
Assim, a semântica desta instrução será: se o valor de condição for verdadeiro então, execute
o bloco de instruções (inst1; ....; instN) ligado à palavra então, e posteriormente, execute a
primeira instrução que estiver após o comando se então que está sendo executado.
Senão, se o valor de condição for falso, então ignore o bloco de instruções ligado a
palavra então, e desvie o controle de execução para a primeira instrução após a instrução se
então que está sendo executado.
FALSO
- - - - - Fluxo a ser seguido se o valor de
de condição for Falso
VERDADEIRO
se condição
então
inst1;
inst2;
inst3;
.........
instN;
instX;
Fluxo a ser seguido se o valor de
de condição for Verdadeiro
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
62
6.3 - EXERCÍCIOS RESOLVIDOS
R.6.l - Dado um número inteiro, calcule o triplo do mesmo caso ele seja positivo ou nulo, ou
o dobro caso ele seja negativo (ver figura 6.2).
ae (num);
as (res);
{num número a ser fornecido}
{res resultado do problema}
objetos num, res : inteiro;
início
leia (num);
se num for maior ou igual a zero, então calcule o seu triplo e armazene o
resultado em res;
se num for menor que zero, então calcule o seu dobro e armazene o resultado
em res;
escreva (res);
fim.
Neste nosso algoritmo, misturamos textos já padronizados na nossa linguagem
algorítmica, com textos descritos em linguagem natural.
De forma algorítmica, isto não é válido, mas é uma técnica muito utilizada no
desenvolvimento de algoritmos, a qual é chamada de refinamentos sucessivos.
As partes do algoritmo que forem descritas em linguagem natural (narrativa) são
refinadas para a linguagem algorítmica numa etapa posterior.
As vantagens disto, é que uma simples frase em linguagem natural pode representar
um grande número de instruções algorítmicas, e com o uso desta técnica, primeiro nós
estruturamos logicamente o algoritmo para depois resolvê-lo definitivamente.
Um outro ponto positivo é a decomposição da solução do problema. Existem
problemas, ou certas partes de um problema, que são de difíceis definições algorítmicas.
Assim, quando estivermos descrevendo um algoritmo que resolva problemas deste tipo, nas
partes mais complicadas, ou mais trabalhosas, simplesmente colocaremos uma frase que nos
indique que naquele ponto tais detalhes ainda deverão ser implementados. E assim, seguimos
na descrição do nosso algoritmo como se todos os detalhes acima já estivessem
implementados (mas não estão) em linguagem algorítmica.
Estes detalhes, ainda não resolvidos, devem ser implementados em um segundo
detalhamento do algoritmo. Só que, a diferença, é que agora nos preocupamos somente com
os pontos que sobraram, e não com todo o algoritmo.
Caso, neste segundo detalhamento, ainda existam dificuldades na implementação
algorítmica dos detalhes ainda não resolvidos, podemos criar os detalhes do detalhe, deixando
a solução algorítmica para um terceiro detalhamento. E assim sucessivamente, até obtermos
um texto coerente com a linguagem algorítmica.
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
63
início
leia (num);
se num >= 0
triplo de num;
se num < 0
dobro de num;
escreva (res);
fim.
Figura 6.2 Fluxograma do exercício resolvido R.6.1
Obviamente que o problema R.6.l. não tem muito de complexo, ou trabalhoso, para
usar a técnica de refinamentos sucessivos (ver figura 6.3); mas nós não poderíamos perder
oportunidade do contexto para inserir esta nova técnica. A solução correta do mesmo é dada a
seguir:
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
64
var num, res : inteiro;
início
leia (num);
se num >= 0 então res  3 * num;
se num < 0 então res  2 * num;
escreva (res);
fim.
início
leia (num);
se num >= 0
res  3*num;
se num < 0
res  2*num;
escreva (res);
fim.
Figura 6.3 Fluxograma do exercício resolvido R.6.1 usando a técnica de refinamentos
sucessivos
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
65
R.6.2 - Uma determinada loja está fazendo promoções de vendas. Qualquer compra que um
cliente fizer até R$ 100,00 receberá 5% de descontos. Se a compra for maior que R$ 100,00,
mas inferior a R$ 200,00, o desconto será de 10%. Se for superior ou igual a R$ 200,00, o
desconto será de 20%.
Faça um algoritmo (ver figura 6.4) que calcule o desconto do total da compra de um cliente, e
informe também, o total a pagar já com os descontos.
Solução 1:
var Tcompra, desconto, Tpagar : real;
início
leia (Tcompra);
se Tcompra <= 100.0 então desconto  (5/100) * Tcompra;
se (Tcompra > 100.0) e (Tcompra < 200.0) então desconto  (10/100) * Tcompra;
se Tcompra >= 200.0 então desconto  (20/100) * Tcompra;
Tpagar  Tcompra - desconto;
escreva (desconto, Tpagar);
fim.
Solução 2:
var Tcompra, desconto, Tpagar : real;
início
leia (Tcompra);
desconto  (5/100) * Tcompra;
{estamos assumindo que o maior parte dos clientes fará sua compra entre R$
100,00 e R$ 200,00. Mas de qualquer maneira iremos verificar se realmente
está nesta faixa, caso tenhamos errado, devemos substituir o valor do
desconto}
se (Tcompra > 100.0) e (Tcompra < 200) então desconto  (5/100) * Tcompra;
se Tcompra >= 200.0 então desconto  (20/100) * Tcompra;
Tpagar  Tcompra - desconto;
escreva (desconto, Tpagar);
fim.
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
66
início
leia (Tcompra);
se Tcompra <= 100
desconto  (5/100)*Tcompra;
se Tcompra > 100
e
Tcompra < 200
desconto  (10/100)*Tcompra;
se Tcompra >= 200
desconto  (20/100)*Tcompra;
Tpagar  Tcompra-desconto;
escreva (desconto, Tpagar);
fim.
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
67
início
leia (Tcompra);
desconto  (5/100)*Tcompra;
se Tcompra > 100
e
Tcompra < 200
desconto  (10/100)*Tcompra;
se Tcompra >= 200
desconto  (20/100)*Tcompra;
Tpagar  Tcompra-desconto;
escreva (desconto, Tpagar);
fim.
Figura 6.4 Fluxogramas das soluções 1 e 2 do exercício resolvido R.6.2
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
68
6.4 - INSTRUÇÃO SE ENTÃO SENÃO
A estrutura se então senão (ver figura 6.5) nos permite fazer uma escolha entre duas
alternativas mutuamente exclusivas.
A sintaxe geral desta instrução é:
bloco de
instruções 1
se condição
então
inst11;
inst12;
inst13;
...........
inst1N;
senão
bloco de
instruções 2
onde:
inst21;
inst22;
inst23;
...........
inst2M;
se então senão é uma instrução de seleção composta.
condição pode ser um identificador do tipo lógico, ou uma expressão
relacional, ou uma expressão lógica.
inst11;...;inst1N forma o conjunto de instruções do bloco de instruções 1
inst21;...;inst2M forma o conjunto de instruções do bloco de instruções 2
A semântica desta instrução, tem a seguinte definição:
Como condição somente poderá fornecer um valor lógico (falso ou verdadeiro), então
temos duas possibilidades para avaliar: ou executamos o bloco de instruções 1 (então), ou
executamos o bloco de instruções 2 (senão), mas qualquer um dos blocos que for executado,
implica na exclusão do outro.
V
inst_11;
inst_12;
......;
inst_1N;
se condição
F
inst_21;
inst_22;
......;
inst_2M;
Figura 6.5 Estrutura SE ENTÃO SENÃO
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
69
Se o valor avaliado de condição for verdadeiro, então o bloco de instruções 1 será
executado e por conseguinte, o bloco 2 será ignorado.
Senão caso o valor avaliado de condição for falso, então o bloco de instruções 2 será
executado, e o bloco 1 será ignorado.
Note que nesta instrução sempre teremos que executar um dos blocos de instruções.
Após a execução de um dos blocos, o controle de execução deve ser transferido para a
primeira instrução que vier após a estrutura se então senão.
FALSO
VERDADEIRO
- - - - - Fluxo a ser seguido se o valor de
condição for falso
se condição
então
inst11;
inst12;
inst13;
……...
inst1N;
Fluxo a ser seguido se o valor de
condição for verdadeiro
senão
inst21;
inst22;
inst23;
..........
inst2M;
instX;
6.5 - EXERCÍCIOS RESOLVIDOS
R.6.3 - Dados dois números inteiros quaisquer, faça um algoritmo que descubra qual o maior
valor entre eles (ver figura 6.6).
Solução:
var num1, num2, maior : inteiro;
início
leia (num1, num2); {Conhecendo os valores dos números}
se num1 > num2
{Caso o 1º. número for maior que o 2º.}
então maior  num1;
senão maior  num2;
{Caso o 2°. número seja maior ou igual ao 1°.}
escreva (maior);
fim.
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
70
INSTRUÇÃO
AÇÃO
num1
num2
leia (num1, num2);
(supondo 5 e 8 como valores)
5
8
se num1 > num2
então maior  num1;
senão maior  num2;
5
8
maior
var num1, num2, maior
8
8
escreva (maior);
início
leia (num1, num2);
se num1 > num2
maior  num1;
maior  num2;
escreva (maior);
fim.
Figura 6.6 Fluxograma do exercício resolvido R.6.3
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
71
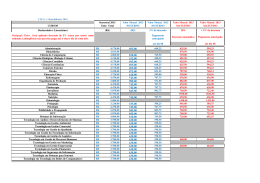
R.6.4 - Faça um algoritmo (ver figura 6.7) que receba como argumento de entrada o total de
ganhos de uma pessoa, em reais, e que calcule o desconto do imposto de renda, segundo a
tabela a seguir:
FAIXA SALARIAL EM R$
até 500,00
de 500,00 até 1.500,00
de 1.500,00 até 2.500,00
acima de 2.500,00
ALÍQUOTA DE DESCONTO
(isento) 0%
10%
15%
25%
refinamento 1
- definir os objetos necessários
- conhecer o total de ganhos da pessoa
- verificar em qual faixa salarial os seus ganhos encontram
- em função da faixa salarial, verificar o % devido para o IR
- calcular o montante que deve ser pago ao IR
- informar o resultado
refinamento 2
ae (Tganho);
as (TpagarIr);
{Tganho = Total de ganhos, em reais}
{TpagarIr = Total a pagar de Imposto de renda}
objetos Tganho, TpagarIr, alíquota : real;
{alíquota = variável auxiliar usada nos cálculos do imposto a pagar, sua função será de
armazenar o percentual do imposto devido}
início
leia (Tganho);
se Tganho <= 500
{se os ganhos da pessoa são até 500,}
então
{então ela é isenta do imposto de renda}
alíquota  0;
senão
{se a pessoa ganha mais de 500 então verifique, qual é a alíquota devida para o IR}
TpagarIr  Tganho * aliquota; {cálculo do IR devido}
escreva (TpagarIr);
fim.
Estamos usando a técnica de refinamentos sucessivos. Definimos, em primeiro lugar,
os objetos e depois tentamos atingí-los passo-a-passo. Desta forma a solução algorítmica fica
mais fácil.
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
72
Apesar de aparecer mais trabalhosa, esta técnica permite escrever algoritmos com
confiabilidade, ou seja, com menor risco de errar. E acredite, ás vezes descobrir um erro em
um algoritmo é mais difícil do que refazê-lo.
refinamento 3
var Tganho, TpagarTr, alíquota : real;
{alíquota = variável auxiliar usada nos cálculos do imposto a pagar, sua função será de
armazenar o percentual do imposto devido}
início
leia (Tganho);
{se os ganhos da pessoa são até 500,}
se Tganho <= 500
então
{então ela é isenta do imposto de renda}
alíquota  0;
senão se Tganho <= 1500 {se não for isenta, qual o % devido para o IR}
então
alíquota  10/100;
senão se Tganho <= 2500
então
alíquota  15/100;
senão
alíquota  25/100;
TpagarIr  Tganho * aliquota; {cálculo do IR devido}
escreva (TpagarIr);
fim.
início
leia (Tganho);
se Tganho <= 500
alíquota  0;
calcular diferença;
TpagarIr  Tganho*alíquota;
escreva (TpagarIr);
fim.
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
73
início
leia (Tganho);
se Tganho <= 500
se Tganho <= 1500
alíquota  0;
se Tganho <= 2500
alíquota  10/100;
alíquota  15/100;
alíquota  25/100;
TpagarIr  Tganho*alíquota;
escreva (TpagarIr);
fim.
Figura 6.7 Fluxogramas do exercício resolvido R.6.4 usando a técnica de refinamentos
sucessivos
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
74
6.5 - EXERCÍCIOS PROPOSTOS
Faça um algoritmo para resolver cada um dos problemas abaixo:
1) Um funcionário ganha P reais por hora normal trabalhada. Sabendo-se que a jornada
normal de trabalho é de 40 horas/semana e que o mesmo ganha 50% a mais sobre o valor da
hora normal, por hora extra trabalhada.
Ao serem fornecidos o valor da hora normal e a quantidade de horas trabalhada na semana.
Calcule: o salário normal semanal, o salário extra e o salário bruto do funcionário.
2) Refaça o exercício 1, considerando que sobre o salário bruto do funcionário incidem as
seguintes taxas:
a) 10% de INSS;
b) Imposto de Renda (IR) de acordo com a seguinte tabela:
faixa salarial R$
até 2.000,00
de 2.000,01 até 3.000,00
de 3.000,01 até 4.500,00
acima de 4.500,00
alíquota de desconto %
isento
8%
10 %
15 %
c) Imposto Sindical 0,5%.
Informe os salários parciais (vantagens), o total das vantagens, os descontos e o salário
líquido do funcionário.
3) Fornecidos 2 valores descobrir qual o maior valor, e colocá-los em ordem crescente.
4) Fornecidos 3 valores descobrir qual o maior valor e o menor valor entre os mesmos.
5) Numa certa loja de eletrodomésticos, o vendedor encarregado da seção de televisores
recebe, mensalmente, um salário fixo mais comissão. Esta comissão é calculada em relação
ao tipo e a quantidade de televisores vendidos por mês, obedecendo a seguinte tabela:
TIPO DE TV
Nº. DE APAR. VEND.
a cores
até 10
mais de l0
até 20
mais de 20
preto-e-branco
COMISSÃO (R$) / APAR. VEND.
5,00
10,00
2,00
4,00
Sobre o seu salário fixo há um desconto de 10% referente ao INSS. Caso o seu salário bruto
exceda a R$ 100,00 haverá desconto de imposto de renda, segunda a tabela abaixo, aplicada
sobre o valor excedente a R$ 100,00.
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
75
FAIXA SALARIAL
ALIQUOTA (%)
até 100,00
de 100,01 até 150,00
mais de 150.00
isento
10
15
Calcule:
a) a comissão do funcionário;
b) o salário bruto do funcionário;
c) os valores de cada desconto;
d) o total dos descontos;
e) o salário líquido.
6) Na linha de montagem de uma fábrica existem 3 classes de operários:
1 - os que montam até 30 peças por mês
2 - os que montam de 31 até 35 peças por mês
3 - os que montam mais de 35 peças por mês
Os operários de classe 1 ganham salário mínimo. Os da classe 2 ganham o mínimo mais uma
comissão de 3% (do salário mínimo) por peça montada acima das 30 iniciais, e os da classe 3,
recebem o mínimo mais 5% por peça acima das 30 iniciais. Calcule o salário bruto do
operário, informando o valor ganho com comissão.
7) Dado um conjunto contendo quatro valores (i, a, b, c), sendo i um valor inteiro, faça:
se i = l, ordene em ordem crescente a,b,c
se i = 2, ordene em ordem decrescente a,b,c
se i = 3, informar os três valores, de forma que o maior valor entre a, b e c fique entre os
outros dois.
Para qualquer outro valor de i divida a soma de a, b e c pelo maior valor entre os mesmos.
8) Dado um par de coordenada cartesiana (X, Y), determinar em que quadrante (ou sobre que
eixo) do sistema cartesiano encontra-se esta coordenada.
Use a seguinte codificação:
VALOR INFORMADO
(0, 0)
(1, 1)
(2, 1)
(-3, -3)
(-4, 4)
(-1, 0)
(0, -2)
SIGNIFICADO
coordenada na origem do sistema
coordenada no quadrante 1
coordenada no quadrante 2
coordenada no quadrante 3
coordenada no quadrante 4
coordenada sobre o eixo X
coordenada sobre o eixo Y
CAPÍTULO 6 - ESTRUTURAS DE SELEÇÃO
76
9) Fornecidos 3 valores inteiros, coloca-los em ordem crescente (utilize o menor número de
comparações (3)).
10) Sabe-se que o dia da semana fornecido entre 1°. de março de 1700 a 28 de fevereiro de
2100, pode ser determinado através do seguinte método:
N = (365,25 * g(a, m)) + (30,6 * f(m)) + d - 621049 ,m))
ds = [N / 7 ]* 7 + C + 1
onde:
d é o dia do mês atual
m é o mês atual
a é o ano atual
ds é o dia da semana (1,2,...,7) 1 é domingo e 7 é sábado
a - 1, se m ≤ 2
g(a, m) = 
a, se m > 2
parte inteira de
m - 13, se m ≤ 2
f(m) = 
m + 1, se m > 2
2, se N < 36523

C = 1, se 36523 ≤ N < 73048
0, se N > 73048

parte fracionária de