Elementos de Hidrologia Aplicada
Prof. Antenor Rodrigues Barbosa Júnior
4. Infiltração
4. INFILTRAÇÃO
4.1. GENERALIDADES
Infiltração é a passagem da água da superfície para o interior do solo. É, pois, um
processo que depende fundamentalmente (a) da disponibilidade de água para infiltrar, (b) da
natureza do solo, (c) do estado da camada superficial do solo e (d) das quantidades de água e ar
inicialmente presentes no interior do solo.
4.2. DESCRIÇÃO DO PROCESSO DE INFILTRAÇÃO – EVOLUÇÃO DO PERFIL DE
UMIDADE
No interior do solo, o espaço disponível para a água se acumular e se movimentar é
determinado pelos vazios existentes entre os grãos que compõem a estrutura do solo. O
parâmetro capaz de especificar a máxima retenção de água no solo é a sua porosidade1, n. O teor
de umidade do solo2, , será sempre menor ou igual à porosidade. O grau de saturação do solo3 é
definido pela relação entre o volume de água e o volume de vazios da amostra.
À medida que a água infiltra pela superfície, as camadas superiores do solo vão se
umedecendo de cima para baixo, alterando gradativamente o perfil de umidade.
Enquanto houver aporte de água, o perfil de umidade evolui e tende à saturação em toda a
profundidade, sendo a superfície, naturalmente, o primeiro nível a saturar. Cumpre observar que,
normalmente, a infiltração decorrente de precipitações naturais não é capaz de saturar todo o
solo, restringindo-se a saturar, quando consegue, apenas as camadas próximas à superfície. Em
consequência, desenvolve-se um perfil típico de umidade, em que o seu teor decresce com a
profundidade, conforme ilustrado na Figura 4.1 (linha cheia da Figura 4.1).
Figura 4.1 – Evolução do perfil de umidade do solo.
Porosidade do solo, n = (volume de vazios)  (volume da amostra de solo)
Umidade do solo,  = (volume de água na amostra de solo)  (volume da amostra de solo)
3
Grau de saturação, S = (volume de água na amostra de solo)  (volume de vazios) = /n
1
2
56
Elementos de Hidrologia Aplicada
Prof. Antenor Rodrigues Barbosa Júnior
4. Infiltração
Quando cessa o aporte de água à superfície (isto é, deixa de haver infiltração), a umidade
no interior do solo se redistribui, evoluindo para um perfil inverso com os menores teores de
umidade próximos à superfície e os maiores nas camadas mais profundas (linha pontilhada da
Figura 4.1). Nem toda a umidade é drenada para as camadas mais profundas do solo, já que parte
é transferida para a atmosfera pela evapotranspiração.
Convém observar que nas camadas inferiores do solo geralmente é encontrada uma zona
de saturação (lençol freático), mas sua influência no fenômeno da infiltração só é significativa se
situa a pouca profundidade.
4.3. GRANDEZA CARACTERÍSTICA DA INFILTRAÇÃO – CAPACIDADE DE
INFILTRAÇÃO
A capacidade de infiltração, f, é o potencial que o solo tem de absorver água pela sua
superfície. A medida da capacidade de infiltração é feita em termos de uma altura de lâmina
d’água, por unidade de tempo: representa, fisicamente, o volume de água que o solo pode
absorver, por unidade de área, na unidade de tempo. A capacidade de infiltração f tem dimensão
de comprimento por tempo e é medida, em geral, em mm/h ou mm/dia.
Deve-se fazer distinção entre os conceitos de capacidade de infiltração e taxa real de
infiltração, dado que esta última só acontece quando há disponibilidade de água para penetrar no
solo. As curvas, em função do tempo, da taxa real de infiltração e da capacidade de infiltração de
um solo somente coincidem quando o aporte superficial de água (proveniente de precipitações e
mesmo de escoamentos superficiais de outras áreas) tem intensidade superior ou igual à
capacidade de infiltração.
Se uma precipitação atinge o solo com uma intensidade (i) menor que a capacidade de
infiltração (f) toda a água penetra no solo, provocando uma progressiva diminuição da própria
capacidade de infiltração. Se a precipitação continua, dependendo da sua intensidade, pode
ocorrer um instante em que a capacidade de infiltração diminui ao ponto de se igualar à
intensidade da precipitação. A partir deste momento, mantendo-se a precipitação, a infiltração
real se processa na mesma taxa da capacidade de infiltração, que passa a decrescer
exponencialmente com o tempo, tendendo a um valor mínimo. Em decorrência, a parcela não
infiltrada da precipitação se escoa pela superfície em direção às áreas mais baixas: na forma de
um balanço, i  f  escoamento superficial.
Cessada a precipitação, e não havendo aporte de água à superfície do solo, a taxa de
infiltração real anula-se rapidamente, enquanto que a capacidade de infiltração volta a crescer,
pois o solo continua a perder umidade para as camadas mais profundas, além das perdas por
evapotranspiração.
Na Figura 4.2 representa-se a evolução da capacidade de infiltração em função do tempo,
em decorrência de uma precipitação de duração td e intensidade i constante. Nota-se que com o
início da chuva a capacidade de infiltração decresce com o tempo. Enquanto f  i toda a água
precipitada infiltra-se no solo. No instante te, contado a partir do início da chuva, a capacidade de
infiltração iguala-se à intensidade da chuva (ponto M na figura). A partir deste ponto, e até o
instante correspondente ao ponto N da figura, a capacidade de infiltração reduz-se
exponencialmente. Parte da água de chuva se infiltra e o restante escoa superficialmente. As
áreas demarcadas na figura representam, conforme indicado, as alturas totais das lâminas d’água
infiltrada e escoada superficialmente.
57
Elementos de Hidrologia Aplicada
Prof. Antenor Rodrigues Barbosa Júnior
4. Infiltração
Figura 4.2 – Visualização da variação da capacidade de infiltração com a ocorrência de uma chuva
4.4. EQUAÇÃO DE HORTON PARA O CÁLCULO DA INFILTRAÇÃO PONTUAL
A partir de experimentos de campo, Horton (1939) estabeleceu, para o caso de um solo
submetido a uma precipitação com intensidade superior à capacidade de infiltração, uma relação
empírica para representar o decaimento da infiltração com o tempo (ramo MN da curva f x t da
Figura 4.2), que pode ser escrita na forma:
f  f C  f 0  f C  exp  k 
(01)
onde
f = capacidade de infiltração (igual à taxa real de infiltração) no tempo genérico ,
f0 = capacidade de infiltração no tempo  = 0,
fC = capacidade de infiltração mínima, ou taxa mínima de infiltração, que é um valor assintótico
(valor final de equilíbrio) avaliado em um tempo  suficientemente grande,
k = constante característica do solo (constante de Horton), com dimensão de tempo-1, e
 = tempo.
4.5. FATORES QUE INTERVÊM NA CAPACIDADE DE INFILTRAÇÃO
São vários os fatores que exercem influência na infiltração da água em um solo. Listamse a seguir cada um deles.
a) Tipo de solo: A capacidade de infiltração varia diretamente com a porosidade do solo, com o
tamanho das partículas do solo (distribuição granulométrica) e o estado de fissuração das
rochas.
b) Grau de umidade do solo: O solo no estado seco tem maior capacidade de infiltração, pelo
fato de que à ação gravitacional se somam as forças capilares. De outro modo, quanto maior
for a umidade do solo, menor será a capacidade de infiltração.
c) Compactação pela ação de homens e animais: A compactação da superfície do solo o torna
mais impermeável, diminuindo a capacidade de infiltração.
d) Ação da precipitação sobre o solo: A ação da chuva sobre o solo tende a diminuir a
capacidade de infiltração, pelo efeito da compactação da superfície do terreno, do transporte
58
Elementos de Hidrologia Aplicada
Prof. Antenor Rodrigues Barbosa Júnior
e)
f)
g)
h)
4. Infiltração
de material fino que diminui a porosidade junto à superfície e do aumento das partículas
coloidais, que diminui os espaços intergranulares.
Alteração da macroestrutura do terreno: A capacidade de infiltração pode ser aumentada
pela alteração da macroestrutura do solo devido a fenômenos naturais, como escavações de
animais, decomposição de raízes de plantas e ação do sol, e também devido a ação do
homem no cultivo da terra (aração).
Cobertura Vegetal: A presença da cobertura vegetal tende a aumentar a capacidade de
infiltração do solo, pois atenua a ação da chuva e facilita a atividade de insetos e outros
animais no processo de escavação. Ainda, por dificultar o escoamento superficial e por retirar
a umidade do solo, possibilita a ocorrência de maiores valores da capacidade de infiltração.
Temperatura do solo: A infiltração é um fenômeno de fluxo de água no solo. Assim, sua
medida (através da capacidade de infiltração) depende da temperatura da água, da qual
depende a sua viscosidade. Menores temperaturas provocam o aumento da viscosidade,
reduzindo f.
Presença de ar: O ar retido temporariamente nos espaços intergranulares retarda a infiltração
da água.
4.6. MEDIÇÃO DA CAPACIDADE DE INFILTRAÇÃO
A capacidade de infiltração de um solo pode ser medida pelo uso de aparelhos
denominados infiltrômetros. Os infiltrômetros são, em geral, de dois tipos: a) os infiltrômetros
propriamente ditos, de anel metálico, que utilizam a aplicação de água por inundação (mantém
sempre um aporte de água à superfície); e b) os simuladores de chuva, que utilizam a aplicação
de água por aspersão.
Os infiltrômetros do primeiro tipo são tubos cilíndricos curtos feitos de chapa metálica,
de diâmetro  entre 20 e 90 cm. Estes são cravados verticalmente no solo, de modo a sobrar uma
pequena altura livre (Figura 4.3).
Existem
duas
variações
do
infiltrômetro de anel metálico, conforme se
utilizam um tubo ou dois tubos concêntricos.
Quando se utilizam dois tubos, o externo
tem o papel de prover a quantidade de água
necessária ao espalhamento lateral devido
aos efeitos de capilaridade. Assim, a
infiltração propriamente dita deve ser
medida levando-se em conta a área limitada
pelo
cilindro
interno.
Durante
o
experimento, mantém-se sobre o solo uma
pequena lâmina de 5 a 10 mm de água, nos
dois compartimentos. Para obter o valor de
f, divide-se a taxa de aplicação da água pela
área da seção transversal do tubo interno.
Figura 4.3 – Infiltrômetro de duplo anel
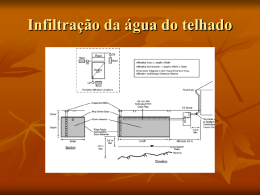
Na Figura 4.4 é representado o infiltrômetro de anel metálico simples em operação. O
dispositivo da figura é constituído de um tubo de 20 cm de diâmetro, alimentado por um vaso de
Mariotte – o vaso de Mariotte permite a adição controlada da água de infiltração, cuja vazão é
determinada pela altura h (na verdade, a vazão é controlada pela altura entre o tubo de sucção do
vaso e a saída da mangueira). O tubo de sucção permite a entrada do ar que vai formar a
“atmosfera à pressão constante” à superfície da água no interior do vaso.
59
Elementos de Hidrologia Aplicada
Prof. Antenor Rodrigues Barbosa Júnior
4. Infiltração
Figura 4.4 – Figura esquemática de um infiltrômetro de anel simples em operação
Como exemplo, apresenta-se uma planilha de anotações e cálculo (Tabela 4.1) de uso nas
medidas da capacidade de infiltração por meio de um infiltrômetro de anel metálico. Os
resultados de cálculo de f em função do tempo são normalmente lançados em um gráfico
cartesiano para mostrar a evolução da capacidade de infiltração ao longo do tempo.
A coluna (4) da Tabela 4.1 é preenchida dividindo-se a coluna (3) pela área A da seção
transversal do infiltrômetro. Por sua vez, a coluna (5) é preenchida dividindo-se os valores
obtidos na coluna (4) pelo intervalo de tempo correspondente em horas.
Tabela 4.1 – Elementos de cálculo da capacidade de infiltração com o uso do infiltrômetro de anel metálico
(1)
(2)
(3)
(4)
(5)
Tempo
(min)
Volume lido
(cm3)
Variação do volume
(cm3)
Altura da lâmina
(mm)
Capacidade de infiltração
(mm/h)
Os principais inconvenientes relacionados ao uso de infiltrômetros, que causam erros nas
medidas, são: i) ausência do efeito de compactação da chuva; ii) fuga do ar retido para a área
externa aos tubos; iii) deformação da estrutura do solo com a cravação dos tubos.
Os infiltrômetros do segundo tipo, chamados de simuladores de chuva, são aparelhos nos
quais a água é aplicada por aspersão, com taxa uniforme superior a f, exceto para um breve
intervalo de tempo inicial. As áreas delimitadas de aplicação da água são normalmente de
formato retangular ou quadrado, de 0,10m2 até 40m2 de superfície. Estas áreas são circundadas
por canaletas que recolhem a água do escoamento superficial. Medem-se, nos testes, a
quantidade de água adicionada e o escoamento superficial resultante, deduzindo-se o valor de f.
4.7. AVALIAÇÃO DA CAPACIDADE DE INFILTRAÇÃO EM UMA BACIA
Para conhecer da capacidade de infiltração média na área de uma bacia hidrográfica,
utiliza-se a equação do balanço hídrico. Se forem conhecidos a precipitação e o escoamento
superficial, poder-se-á calcular, por diferença, a capacidade de infiltração da bacia. Neste
60
Elementos de Hidrologia Aplicada
Prof. Antenor Rodrigues Barbosa Júnior
4. Infiltração
procedimento admite-se que a evapotranspiração durante a chuva é muito pequena. Assim,
f  i  QS A , onde QS é a vazão devida ao escoamento superficial e A é a área de drenagem da
bacia hidrográfica.
Na avaliação acima, acaba-se por incluir a interceptação e o armazenamento nas
depressões do terreno no valor de f calculado. Para as pequenas bacias, o erro introduzido é
menos significativo do que para as grandes bacias.
Para fins de cálculo, pode-se organizar uma planilha de anotações como a da Tabela 4.2.
Nesta tabela:
coluna (4) = coluna (3)  área da bacia (corrigindo-se as unidades),
coluna (5) = coluna (2)  intervalos correspondentes de tempo (corrigindo-se as unidades),
coluna (6) = coluna (5)  coluna (4).
Tabela 4.2 – Elementos de cálculo da capacidade de infiltração em uma bacia hidrográfica
(1)
(2)
Tempo, Precipitação,
t
P
(min)
(mm)
(3)
Escoamento
Superficial, Q
(m3/s)
(4)
Escoamento
Superficial, qs
(mm/h)
(5)
Intensidade
da chuva, i
(mm/h)
(6)
Capacidade de
infiltração, f
(mm/h)
EXEMPLO 4.1
Um experimento com simulador de chuva foi realizado para a determinação da equação de
Horton para a capacidade de infiltração de um determinado solo. A chuva artificial foi produzida
com uma intensidade constante de 38mm/h. O excesso, isto é, a quantidade não infiltrada
(escoada superficialmente), foi recolhido nas canaletas que circundam a área de teste e
conduzido para um reservatório, permitindo a determinação dos volumes não infiltrados ao longo
do tempo. Um resumo dos resultados do teste é apresentado na Tabela 4.3.
Tabela 4.3 – Dados do experimento com simulador de chuva
t (min)
0
6
10
14
18
22
26
30
34
38
42
i (mm/h)
38
38
38
38
38
38
38
38
38
38
38
Vols ()
0,00
0,00
1,93
7,96
14,99
23,92
34,55
45,68
57,71
69,84
82,17
Sabendo-se que a área de teste é de 10m2 e que, após um longo tempo de ensaio, a vazão total na
canaleta que conduz o excesso ao reservatório manteve-se constante e igual a 56m/s, ajustar a
equação de Horton.
Obs: o escoamento superficial teve início no instante t = 6min.
Solução
Desprezando-se as perdas por evaporação, a equação do balanço hídrico para a área em questão
produz os valores das taxas reais instantâneas de infiltração:
i  t  A  Q  t  Vol
ou
i
Q 1 Vol

.
A A t
(02)
O termo do 2o membro da Eq. (02) representa a taxa real de infiltração, sendo Vol o volume
infiltrado num intervalo de tempo t.
61
Elementos de Hidrologia Aplicada
Prof. Antenor Rodrigues Barbosa Júnior
4. Infiltração
Fazendo qs = Q/A e h=Vol/A, tem-se
i  qs 
h
,
t
(03)
com h representando a altura da lâmina infiltrada no intervalo t. Para obter as taxas reais de
infiltração, constrói-se a Tabela 4.4. Note que a taxa real de infiltração só representa a
capacidade de infiltração a partir do momento em que se tem a saturação da camada superficial
do solo, identificado no problema como o instante em que passa a ocorrer o escoamento
superficial (isto é, para t  6min, f = h/t). Uma visualização gráfica dos resultados
encontrados é feita na Figura 4.5.
Tabela 4.4 – Elementos de cálculo da capacidade de infiltração em teste com simulador de chuva
t
(min)
i
(mm/h)
VolS
()
VolS
()
Q=VolS/t
(/h)
qs=Q/A
(mm/h)
h/t
(mm/h)
= tt0
(min)
f
(mm/h)
0
6
10
14
18
22
26
30
34
38
42
38
38
38
38
38
38
38
38
38
38
38
0
0
1,93
7,96
14,99
23,92
34,55
45,68
57,71
69,84
82,17
0,00
1,93
6,03
7,03
8,93
10,63
11,13
12,03
12,13
12,33
0,00
0,00
28,95
90,45
105,45
133,95
159,45
166,95
180,45
181,95
184,95
0,00
0,00
2,895
9,045
10,545
13,395
15,945
16,695
18,045
18,195
18,495
38,00
38,00
35,105
28,955
27,455
24,605
22,055
21,305
19,955
19,805
19,505
0
4
8
12
16
20
24
28
32
36
38,00
35,105
28,955
27,455
24,605
22,055
21,305
19,955
19,805
19,505
40
i
f
i, q, f (mm/h)
30
20
10
q
0
0
5
10
15
20
25
30
35
40
45
tempo, t (min)
Figura 4.5 – Evolução temporal da intensidade da precipitação, do deflúvio superficial e da capacidade de
infiltração.
A equação de Horton deve, então, ser ajustada aos dados das duas últimas colunas da Tabela 4.4.
Assim, da Eq. (01):


f  f C  f 0  f C  exp  k  .
62
Elementos de Hidrologia Aplicada
Prof. Antenor Rodrigues Barbosa Júnior
4. Infiltração
Com os da Tabela 4.4, f0 = 38mm/h e  = t – 6min. Uma informação adicional fornecida no
problema é que, para t (ou ) grande, Q = 56m/s  qs = 20,16mm/h. Da Eq. (03), para qs =
constante, h/t = constante = fC. Isto é, fC = 38,00 – 20,16 = 17,84mm/h. Portanto, conhecidos
f0 e fC, o problema se resume a obter o parâmetro k da equação de Horton.
A Eq. (01) pode ser rearranjada e escrita na forma:
 f  fC 
ln 
  k   ,
f0  fC 
(04)
 f  fC 
log 
  k    log e
f0  fC 
(05)
ou
do tipo Y = k . O coeficiente k pode, então, ser obtido graficamente, ou por meio de análise de
regressão pelo método dos mínimos quadrados. Do gráfico da Figura 4.6, com as ordenadas em
escala logarítmica, tem-se:
- para t1 = 5min  y1 = (f-fC)/(f0-fC) = 0,72,
e
- para t2 = 25min y2 = (f-fC)/(f0-fC) = 0,16.
Da Eq. (04),
ln 0,72 = -k5
e
ln 0,16 = -k25
donde,
ln (0,72/0,16) = k (25-5)  k = 0,075min-1 = 4,5h-1.
f  17,84  38,00  17,84 exp  4,5
f = 17,84  20,16 exp  4,5
com f em mm/h para  em h.
y = (f-fC)/(f0-fC)
1
0,1
0,01
0
10
20
30
40
 (min)
Figura 4.6 – Visualização da evolução da capacidade de infiltração ao longo do tempo e linha de melhor
ajuste do modelo de Horton.
63
Elementos de Hidrologia Aplicada
Prof. Antenor Rodrigues Barbosa Júnior
4. Infiltração
EXERCÍCIOS
4.1) Trace, qualitativamente, a evolução da capacidade de infiltração de um solo com o tempo
de ocorrência de uma chuva de intensidade constante, identificando dois parâmetros da equação
de Horton.
4.2) Que fatores afetam a capacidade de infiltração de um solo?
4.3) Um solo tem equação de infiltração de Horton dada por f  9,1  7,5  e 0,11t , sendo f medido
em mm/h e t em h. Sabendo-se que, para a região, a equação de chuvas intensas é do tipo
0 ,78
i  1500 Tr0 ,12 25  t d  , com i em mm/h, Tr em anos e td em minutos, pede-se: a) a
probabilidade de que este solo seja inundado em um ano qualquer por uma chuva de duração td =
12h; b) a duração de uma chuva de 10 anos de recorrência, capaz de inundar o solo em questão.
R: a) P{Xx}=0,43%; b) td=7,23h
4.4) Durante um certo ano, os seguintes dados hidrológicos foram coletados numa bacia
hidrográfica de 350km2 de área de drenagem: precipitação total de 850mm, evapotranspiração
total de 420mm e escoamento superficial de 225mm. Calcule o volume de infiltração, em metros
cúbicos, desprezando as variações no armazenamento superficial da água.
4.5) Considere os dados das tabelas abaixo. Com base nestes, ajustar a equação de Horton.
t (min)
i (mm/h)
t (min)
h (mm)
0
0,00
0-6
38
6-10
55
6
3,80
10-14
55
10
6,14
14-18
55
14
8,07
18-22
55
18
9,90
22-26
55
22
11,54
h=lâmina infiltrada (acumulada)
26-30
55
26
13,01
30-34
55
30
14,43
34-38
55
34
15,76
38-42
55
38
17,08
42
18,38
R: f17,96(38,0017,96)exp(4,478t)
4.6) A capacidade de infiltração de uma pequena área de solo no início de uma chuva era de
4,5mm/h, e decresceu exponencialmente, seguindo a lei de Horton, até praticamente atingir o
equilíbrio no valor de 0,5mm/h depois de 10h. Sabendo-se que um total de 30mm de água
infiltrou-se durante o intervalo de 10h, estimar o valor do parâmetro k de Horton. R: k  0,103 h-1
4.7) Para o estudo da infiltração em um solo foi realizado um experimento em que se utilizou de
um simulador de chuva em uma área retangular de 4m x 12,5m. A duração desta chuva foi tal
que gerou um escoamento superficial praticamente constante de 0,5/s. Sabendo-se que a
intensidade da chuva artificial era de 50mm/h, pede-se: a) o escoamento superficial, em mm/h, e
a capacidade de infiltração mínima encontrada no experimento; b) o valor da constante de
Horton, considerando que 10 horas após o início da produção do escoamento superficial a
capacidade de infiltração era de 27,2mm/h.
R: a) hs=36mm/h, fmín=14mm/h; b) k=0,1h-1.
4.8) Estime a taxa de infiltração em um determinado solo na cidade de Ouro Preto, ao final de
uma chuva de projeto. Sobre esta chuva sabe-se que a sua duração é de 8h e a probabilidade de
que sua intensidade seja superada em cada ano é de 20%. A respeito do solo em questão sabe-se
que o parâmetro de Horton vale k=0,667h-1 e que, após três horas de precipitação, sua
capacidade de infiltração cai à metade do seu valor inicial. A tabela abaixo representa a análise
de Pfafstetter para as chuvas de 8 horas em Ouro Preto.
1
2
3
4
5
10
15
20
Tr (anos)
52
63
67
70
75
87
92
99
P (mm)
Obs: Admitir a ocorrência do encharcamento imediato da camada superficial do solo com o início da chuva.
R: f8=3,98mm/h
64