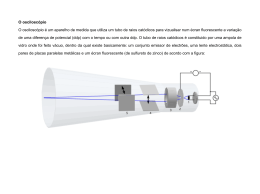
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
Física Experimental (Engenharia Informática)
2008/09 – 1º Semestre
Trabalho 2 – Instrumentos de medida II
O osciloscópio1
Medição de grandezas eléctricas variáveis no tempo
Objectivo: Fundamentar a utilização do osciloscópio para a medição de grandezas eléctricas.
Introdução
Na actividade experimental anterior utilizámos uma interface acoplada a um
computador para a observação de sinais eléctricos variáveis no tempo. Como na
altura se referiu, a medição de tensões variáveis no tempo começou a ser feita,
muito antes da existência de qualquer computador, utilizando osciloscópios,
aparelhos que, ainda hoje, são peças fundamentais de qualquer laboratório onde se
meçam grandezas eléctricas. A capacidade de utilizar correctamente este tipo de
equipamento é portanto um dos objectivos a atingir em qualquer curso laboratorial
básico de Física, sendo para tal fundamental compreender os seus princípios
básicos de funcionamento. Acresce que estes princípios são, por si só,
suficientemente interessantes, para justificar, também desse ponto de vista, o
estudo do funcionamento do osciloscópio.
A peça essencial de um osciloscópio é um tubo de raios catódicos (figura 1),
tubo de vidro no qual se fez o vazio e que contém:
•
•
•
•
Um canhão de electrões, que gera um feixe de electrões de alta velocidade;
Um par de eléctrodos para desvio vertical do feixe (placas de desvio vertical);
Um par de eléctrodos para desvio horizontal do feixe (placas de desvio
horizontal);
Um écran fluorescente, que brilha quando é atingido pelos electrões.
Feixe de
electrões
Placas de desvio
vertical
P1
ponto
brilhante
P2
écran
Vácuo
P2
P1
Placas de desvio
horizontal
Canhão de
electrões
Figura 1. Um tubo de raios catódicos
O canhão de electrões: regulação da intensidade (ou brilho) e da focagem
1
Texto elaborado por J.Maia Alves (Curso de 2004/05)
Trabalho2_200809.doc
VE - Física Experimental
1
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
Física Experimental (Engenharia Informática)
2008/09 – 1º Semestre
Os electrões são emitidos (figura 2) pela superfície de um cátodo aquecido por um
filamento (efeito termiónico). Em frente do cátodo, um outro eléctrodo (cilindro
de Whenelt) com um pequeno orifício serve para limitar o número de electrões que
por ele passam: se lhe for aplicada uma diferença de potencial (tensão) Vw muito
negativa (relativamente ao cátodo), repele quase todos os electrões, e origina um
feixe pouco intenso - e portanto um ponto no écran, onde os electrões incidem, com
pouco brilho. Uma tensão menos negativa deixa passar muitos mais electrões,
produzindo um feixe intenso e um ponto muito luminoso no écran.
Vacel
(ânodo)
Filamento para aquecimento
do cátodo
Vk
(cátodo)
Vw<Vk
(brilho)
Feixe de electrões
energia -e(Vac-Vk)
intensidade regulada
Vw focado no alvo
Vfoc
com
com
por
por
Vfoc
(focagem)
Figura 2 - Um canhão de electrões
O feixe de electrões originados no cátodo é em seguida acelerado por uma
tensão fixa, da ordem dos milhares de volt, de um ânodo oco. A forma do ânodo é
tal que funciona também como uma lente convergente; a “distância focal” desta
lente electrostática pode ser regulada variando a tensão Vfoc de um eléctrodo
cilíndrico intermédio.
As placas de desvio
Ao passar entre duas placas paralelas entre as quais foi aplicada uma tensão
Vd, um electrão sente uma força F ≈ -e Vd /(distância entre as placas), que o
desvia, fazendo-o aproximar-se da placa ligada ao potencial positivo e, portanto,
atingir o écran desviado de y relativamente ao ponto de impacte quando V=0. É
fácil demonstrar que o desvio y do feixe de electrões é proporcional a Vd, pelo que
uma medida de y no écran é uma medição de Vd, uma vez conhecida a escala - ou
seja, a constante de proporcionalidade k, envolvida na relação Vd = ky. Vemos assim
que podemos utilizar um dispositivo deste tipo para desempenhar a função de
voltímetro. Este voltímetro é, de facto, um voltímetro muito especial porque o seu
“ponteiro” é um feixe de electrões, partículas com massa muito reduzida e que,
portanto, respondem muito rapidamente a tensões variáveis no tempo.
Trabalho2_200809.doc
VE - Física Experimental
2
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
Física Experimental (Engenharia Informática)
2008/09 – 1º Semestre
Suponhamos então que aplicamos uma tensão entre as duas placas de desvio
vertical. Uma vez que estas placas se encontram colocadas horizontalmente (ver
figura 1), o desvio do feixe dar-se-á segundo a direcção vertical (para cima ou para
baixo consoante a placa que for ligada ao potencial positivo). Analogamente, quando
aplicamos uma tensão entre as placas de desvio horizontal (colocadas
verticalmente) o feixe de electrões desviar-se-á segundo a horizontal (para a
esquerda ou para a direita). Vemos assim que um tubo de raios catódicos é, de
facto, um duplo voltímetro, cujas entradas são os dois conjuntos de placas de
deflexão, e através do qual podemos medir duas tensões medindo dois desvios do
ponto de impacte do feixe de electrões no écran segundo duas direcções
perpendiculares entre si. Quando utilizamos um osciloscópio aproveitando esta
função de duplo voltímetro dizemos que o utilizamos em modo XY.
Observação da forma de variação v(t) de um sinal.
Como anteriormente se disse o osciloscópio é extremamente útil porque
podemos utilizá-lo para observar a forma de variação temporal de um sinal de
tensão. Essa possibilidade decorre, como também já se disse, do facto de os
electrões que utilizamos para a visualização da medida terem uma massa muito
reduzida e responderem portanto muito rapidamente às forças electrostáticas que
lhes são aplicadas. No entanto, um tubo de raios catódicos, por si só, não nos
permite fazer essa observação porque, como se viu, apenas desempenha o papel de
um duplo voltímetro.
Para compreender como podemos transformar um tubo de raios catódicos
num “traçador de gráficos” V(t) podemos começar por pensar o que realmente
fazemos quando traçamos um gráfico desse tipo: fazemos medições de V em
função do tempo e marcamos os pontos obtidos num referencial cartesiano. Num
gráfico deste tipo o desvio de um dado ponto relativamente à origem é, segundo a
vertical, proporcional à tensão (como acontece com o desvio do ponto no écran do
osciloscópio quando aplicamos o sinal às placas de deflexão vertical), e, segundo a
horizontal, proporcional ao tempo. Se pretendermos visualizar a variação temporal
do sinal que estamos a aplicar às placas de desvio vertical basta-nos, portanto,
fazer com que o ponto de impacte dos electrões no écran se desloque
horizontalmente com uma velocidade constante. Esta função é desempenhada pela
base de tempo do osciloscópio.
Quando pretendemos utilizar um osciloscópio para visualizar a variação
temporal de um sinal deixamos de ter acesso exterior às placas de desvio
horizontal que passam a estar internamente ligadas à tensão gerada pela base de
Trabalho2_200809.doc
VE - Física Experimental
3
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
Física Experimental (Engenharia Informática)
2008/09 – 1º Semestre
tempo, um gerador de sinal em dente de serra, ou seja, com uma forma do tipo da
que se representa na figura 3.
v(t)
t
Figura 3 - Tensão em dente de serra da base de tempo
Com esta tensão aplicada, o ponto deslocar-se-á com velocidade uniforme
desde a extremidade esquerda do écran até à direita, para reaparecer à esquerda
e repetir o ciclo. Note-se que, dentro de cada varrimento de écran, vBT(t) é
proporcional ao tempo (vBT(t)=kt) e, consequentemente, o mesmo acontece com o
desvio horizontal do feixe. A constante de proporcionalidade k é controlada pelo
utilizador que, assim, pode fazer com que o varrimento de écran seja feito com
maior ou menor velocidade consoante pretenda observar sinais com variações mais
ou menos rápidas.
Suponhamos então que pretendemos visualizar um sinal repetitivo, como seja,
por exemplo, um sinal sinusoidal V (t ) = V0 sen(ωt ) . Suponhamos, além disso, e para
simplificar, que esse sinal tem um período T = 1 2πω exactamente igual ao período
do sinal em dente de serra aplicado pela base de tempo às placas de deflexão
horizontal, como se representa na figura 4.
v(t) / ua
2
1
0
-1
-2
sinal visto no écran
tensão plac. desv. horiz.
0
5
1 0
1 5
2 0
2 5
3 0
t / m s
2
1
1
2
3
0
-1
-2
0
5
1 0
1 5
2 0
2 5
3 0
t / m s
2
1 = 2 = 3 : im a g e m
1
e s tá v e l
0
-1
-2
0
2
4
6
8
1 0
t / m s
Trabalho2_200809.doc
VE - Física Experimental
4
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
Física Experimental (Engenharia Informática)
2008/09 – 1º Semestre
Figura 4 – Sinal sinusoidal e sinal em dente de serra com a mesma frequência; nesta
situação a imagem será traçada sempre na mesma posição do écran do osciloscópio em
varrimentos sucessivos.
v(t) / ua
Nesta situação muito particular, a imagem descrita pelo ponto luminoso sobre
o écran do osciloscópio será sempre traçada exactamente na mesma posição em
varrimentos sucessivos, ou seja, obteremos no écran uma imagem estável no tempo
que é, de facto, um gráfico da variação temporal da tensão aplicada nas placas de
deflexão vertical. Num caso mais geral, no entanto, a frequência do sinal a estudar
não será igual à frequência do sinal em dente de serra (nem a um seu múltiplo
inteiro). Obteremos então uma situação equivalente àquela que se representa na
figura 5.
1
0
-1
-2
sinal visto no écran
tensão plac. desv. horiz.
0
5
10
15
20
25
30
t / m s
2
1
1
2
3
0
-1
-2
0
5
10
15
20
25
30
t / m s
2
im a g e m
1
c o r r e p a r a a d ir e it a n o é c r a n
1
0
3
-1
-2
0
2
4
6
8
10
t / m s
Figura 5 – Sinal sinusoidal e sinal em dente de serra com frequências diferentes; nesta
situação a imagem já não será traçada sempre na mesma posição do écran do osciloscópio
em varrimentos sucessivos, dando ao utilizador a sensação de estar “a correr” para a
direita ou para a esquerda consoante o período do sinal a observar for maior ou menor que
o período do sinal em dente de serra.
Varrimentos sucessivos darão agora origem a imagens não coincidentes, já
que corresponderão a troços diferentes da sinusóide. Se a diferença de períodos
for suficientemente pequena, observar-se-á um sinal sinusoidal que “corre”
lentamente no écran, para a direita ou para a esquerda, consoante o período do
sinal a observar for maior ou menor que o período do sinal em dente de serra.
Quanto maior for a diferença de períodos mais acentuado será este efeito,
chegando-se rapidamente a uma situação em que não é sequer possível identificar
de que tipo é o sinal que pretendemos medir. Vemos assim que, a menos que este
Trabalho2_200809.doc
VE - Física Experimental
5
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
Física Experimental (Engenharia Informática)
2008/09 – 1º Semestre
problema seja de alguma forma corrigido, a medição de sinais com o osciloscópio
será, em geral, impossível. Essa correcção é efectuada pelo sistema de disparo (ou
trigger), que seguidamente se descreve.
O sistema de disparo de um osciloscópio garante que, em varrimentos
sucessivos, são traçados no écran troços equivalentes do sinal a medir,
independentemente da diferença existente entre a frequência desse sinal e do
sinal aplicado nas placas de deflexão horizontal. Para isso, actua sobre a base de
tempo, forçando-a a manter o feixe imóvel no lado esquerdo do écran o tempo
suficiente para que o sinal de entrada volte a cruzar um dado valor (zero no caso
representado na figura 6) com uma dada derivada (positiva no caso representado).
v(t) / ua
2
1
0
-1
-2
sinal visto no écran
tensão plac. desv. horiz.
0
5
1 0
1 5
2 0
2 5
3 0
t / m s
2
1
1
2
3
0
-1
-2
0
5
1 0
1 5
2 0
2 5
3 0
t / m s
2
1 = 2 = 3 : im a g e m
1
e s tá v e l
0
-1
-2
0
2
4
6
8
1 0
t / m s
Figura 6 – Ilustração do princípio de funcionamento do sistema de disparo.
Vemos assim que o sistema de disparo faz com que a base de tempo gere um
sinal como o que se representa na figura 6, que se obtém do sinal em dente-deserra introduzindo tempos de espera durante os quais a saída do gerador se
mantém constante (e negativa). Naturalmente, a duração do tempo de espera
efectuado antes de cada varrimento (que se assinala a branco na figura), depende
da diferença entre os períodos do sinal a medir, e do sinal em dente de serra puro
que seria gerado pela base de tempo sem intervenção do sistema de disparo.
Descrição do equipamento disponível
Existem no mercado diversos modelos de osciloscópios. Desde que se
compreenda bem o princípio de funcionamento anteriormente descrito, e
exceptuando casos muito particulares de aparelhos mais sofisticados, a sua
utilização é perfeitamente equivalente, bastando pouco tempo de contacto com um
Trabalho2_200809.doc
VE - Física Experimental
6
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
Física Experimental (Engenharia Informática)
2008/09 – 1º Semestre
dado modelo para que o utilizador o possa utilizar convenientemente. Nesta
actividade experimental iremos utilizar diferentes modelos de osciloscópios
Hameg, todos eles com pequenas diferenças nos respectivos painéis. A descrição
que se segue é baseada no modelo HM203-7.
Na figura 7 encontra-se uma representação esquemática do painel deste
osciloscópio. Como se pode observar, o painel encontra-se dividido em três grandes
regiões delimitadas que agrupam botões com funções relacionadas. A descrição
detalhada sobre todos eles, tal como é fornecida pelo fabricante encontra-se em
anexo. Descreveremos seguidamente a função dos mais importantes.
Figura 7 – Representação esquemática do painel de um osciloscópio Hameg HM203-7.
A região que contém os botões numerados de 1 a 17 agrupa as funções básicas
relacionadas com ligação (1), ajuste de brilho (2) e focagem (4), selecção do modo
de funcionamento (XY ou base de tempo) (5), controlo da constante da base de
tempo (12 e 13), e controlo do sistema de disparo (9, 10, 11, 14, 16 e 17). Note-se
que, para as diferentes posições do comutador 12, a velocidade de varrimento que
lhe corresponde (tempo por cm percorrido pelo feixe no écran) se encontra
indicada na região marcada a cinzento que circunda o comutador. Estas velocidades
só serão reais se o potenciómetro 13 se encontrar na posição CAL. Nesta região
encontra-se ainda um potenciómetro (6) que permite posicionar horizontalmente o
ponto de impacte do feixe de electrões no écran.
Na região que se encontra por baixo do écran, está disponível um comutador
que permite multiplicar por dez a velocidade de varrimento seleccionada no
Trabalho2_200809.doc
VE - Física Experimental
7
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
Física Experimental (Engenharia Informática)
2008/09 – 1º Semestre
comutador 12. Além disso, encontram-se igualmente disponíveis nesta região dois
sinais quadrados com amplitudes standard para verificação da calibração das
escalas (horizontal e vertical).
Finalmente, na região onde se encontram os botões numerados de 21 a 36,
encontram-se as fichas que dão acesso às placas de deflexão vertical (23) e
horizontal (34)∗ através da ligação das pontas de prova que descreveremos adiante,
dois comutadores (25 e 30) semelhantes ao que permite controlar a velocidade de
varrimento, agora para ajustar a escala vertical de cada um dos canais (por
exemplo, volt por centímetro), dois conjuntos de dois botões (22, 35) que
permitem curto-circuitar as placas de deflexão vertical (para ajustar o zero com
os potenciómetros 21 e 36) e filtrar (ou não) a componente contínua do sinal a
medir. As escalas seleccionadas pelos comutadores 25 e 30 podem igualmente ser
multiplicadas por um factor 5 pressionando, respectivamente, os botões 26 e 32.
B
A
Figura 8 – Ponta de prova de um osciloscópio.
Como já se disse, a ligação dos sinais às placas de deflexão é feita utilizando
pontas de prova ligadas através de um ficha BNC às entradas 23 e 34. Uma destas
pontas de prova encontra-se na figura 8. Deve ter-se sempre presente que o
terminal A da ponta de prova se encontra ligado ao chassis do osciloscópio e,
portanto, à terra de protecção do edifício através da ficha de ligação dos 220V.
Nestas condições, as duas entradas do osciloscópio não são entradas puramente
diferenciais, no sentido em que partilham um terminal comum.
∗
Quando utilizamos o osciloscópio no modo de funcionamento com base de tempo, esta entrada, usada
no modo X-Y para actuar nas placas de desvio horizontal, é agora aproveitada para se medir outro sinal,
independentemente da entrada (23). Quer dizer, é agora possível observar no écran do osciloscópio
simultaneamente dois sinais, vyA(t) e vyB(t), introduzidos respectivamente nas fichas (23) e (34). Ambas as
entradas são portanto agora ligadas às placas de desvio vertical, mas nunca simultaneamente: é sempre
aplicada às placas ora o sinal que entra em (23), ora o que entra em (34).
Trabalho2_200809.doc
VE - Física Experimental
8
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
Física Experimental (Engenharia Informática)
2008/09 – 1º Semestre
Actividades experimentais
Actividade experimental nº1
Objectivo: Explorar o funcionamento do osciloscópio: modo XY.
Colocando o osciloscópio em modo XY, utilize a fonte de alimentação (e o gerador de
sinais se assim entender) para estudar a função dos diferentes botões de comando
anteriormente referidos. Verifique a linearidade do desvio do feixe segundo as duas
direcções com a tensão aplicada, e confira o valor das escalas afixadas no painel.
Actividade experimental nº2
Objectivo: Efectuar medições de tempo, e de tensão com o osciloscópio.
Meça a frequência e a amplitude do sinal quadrado de teste disponível no painel do
osciloscópio (19). Verifique o efeito de descalibrar a base de tempo e os amplificadores
verticais (botões 13, 24 e 32).
Utilizando agora o gerador de sinais, observe um sinal quadrado com 10kHz, 5V de
amplitude e um ciclo de trabalho de 50% e outro de 10%.
Actividade experimental nº3
Objectivo: Estudar um circuito simples utilizando um osciloscópio.
Monte o circuito representado esquematicamente.
Utilizando um sinal sinusoidal de 1kHz com 10V de amplitude,
observe os dois sinais de tensão (à saída do gerador de sinais
e
V(t)
aos terminais da resistência) e interprete-os. Como seria o
sinal aos terminais de R se invertesse a posição do díodo (ou
seja, se o rodar de 180º)? Confirme experimentalmente.
Repita o estudo anterior invertendo a posição do díodo. Repita agora trocando a ordem dos
componentes.
Actividade experimental nº4
Objectivo: Visualização da curva i-v do díodo no osciloscópio usando o modo XY.
Monte um circuito com uma resistência de 220 Ω e um LED a um gerador de sinais.
Aplique uma tensão alternada sinusoidal e observe a dependência da tensão aos terminais
do LED vLED(t) no osciloscópio.
1.Qual a tensão necessária para acender o LED?
2.Qual a frequência do sinal a que deixa de observar “variações “ da intensidade
luminosa do LED?
3.Use o modo XY para visualizar a curva característica I versus V para o LED.
Trabalho2_200809.doc
VE - Física Experimental
9
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
Física Experimental (Engenharia Informática)
2008/09 – 1º Semestre
ANEXO
Trabalho2_200809.doc
VE - Física Experimental
10