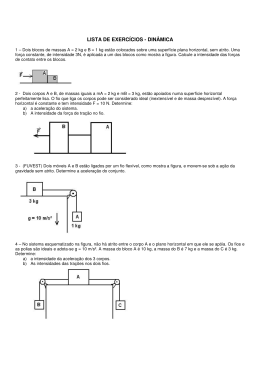
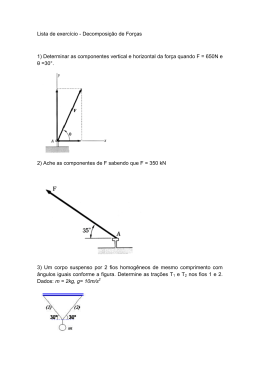
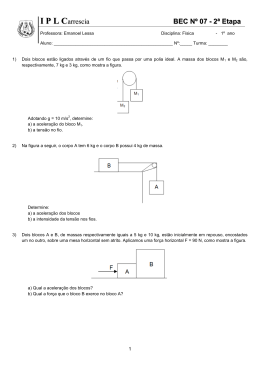
Capítulo 5 – Forças em Dinâmica F=m.a 5 – Forças em Dinâmica A Dinâmica é a parte da Mecânica que estuda os movimentos e as causas que os produzem ou os modificam. Noção de massa e força. Galileu (contradizendo Aristóteles): a tendência natural dos corpos, livre da ação de forças, é permanecer em repouso ou em movimento retilíneo uniforme. Isaac Newton aceitou e desenvolveu as idéias de Galileu. Em sua obra Princípios Matemáticos de Filosofia Natural, enunciou as três leis fundamentais do movimento, conhecidas hoje como LEIS DE NEWTON. 1 – Princípio da inércia (primeira lei de Newton) UM PONTO MATERIAL ISOLADO ESTÁ EM REPOUSO OU EM MOVIMENTO RETILÍNEO UNIFORME. Um ponto material é chamado isolado quando não existem forças atuando nele ou quando as forças aplicadas ao ponto têm soma vetorial nula. FORÇA É A CAUSA QUE PRODUZ NUM CORPO VARIAÇÃO DE VELOCIDADE E, PORTANTO, ACELERAÇÃO. Significa que a força resultante F produz uma aceleração a com mesma direção e mesmo sentido da força resultante e suas intensidades são proporcionais. Da equação fundamental concluímos que, se aplicarmos em corpos de massas diferentes a mesma força resultante, o corpo de maior massa adquirirá aceleração de menor módulo, isto é, o corpo de maior massa resiste mais a variações em sua velocidade. Por isso, a massa é a medida de inércia de um corpo. MASSA X PESO F=m.a P=m.g O PESO DE UM CORPO É A FORÇA DE ATRAÇÃO QUE A TERRA EXERCE SOBRE ELE. A massa é uma propriedade invariante do corpo, enquanto seu peso tem intensidade que depende do valor local de g e varia, ainda que pouco, de um local para outro da Terra. A massa é medida em quilogramas, e o peso, que é uma força, tem sua intensidade medida em newtons. FORÇAS DE CONTATO E FORÇAS DE CAMPO Forças de contato: INÉRCIA: propriedade da matéria de resistir a qualquer variação em sua velocidade.` 2 – Princípio fundamental da Dinâmica (segunda lei de Newton) A RESULTANTE DAS FORÇAS APLICADAS A UM PONTO MATERIAL É IGUAL AO PRODUTO DE SUA MASSA PELA ACELERAÇÃO ADQUIRIDA. Forças de campo: 1
Capítulo 5 – Forças em Dinâmica Exercícios 1 – Nas figuras a seguir, as forças que agem sobre as partículas têm todas o mesmo módulo. As partículas estão todas em movimento. Qual delas está em movimento retilíneo uniforme? 2 – Um objeto encontra‐se em repouso num plano horizontal perfeitamente liso. Num instante t0 uma força horizontal de módulo constante é aplicada ao objeto. Sob a ação dessa força o objeto é acelerado e, num instante posterior t, quando a velocidade do objeto é v, a força é retirada. Após o instante t, o objeto: a) Pára imediatamente; b) Adquire movimento acelerado; c) Prossegue em MRU com velocidade v. Qual das afirmações é correta? 3 – Um ponto material de massa igual a 2kg parte do repouso sob a ação de uma força constante de intensidade 6N, que atua durante 10s, após os quais deixa de existir. Determine: a) A aceleração nos 10s iniciais; b) A Velocidade ao fim de 10s. 4 – Nas figuras a seguir, representamos as forças que agem nos blocos (todos de massa igual a 2,0kg. Determine, em cada caso, o módulo da aceleração que esses blocos adquirem. 3 – Princípio da Ação e Reação (terceira Lei de Newton) Toda vez que um corpo A exerce uma força FA num corpo B, este também exerce em A uma fora FB tal que essas forças: a)
b)
c)
d)
2
Têm a mesma intensidade (módulo); Têm a mesma direção; Têm sentidos opostos; Têm a mesma natureza, sendo ambas de campo ou ambas de contato. Uma das forças é chamada de ação e a outra é de reação. Tais forças não estão aplicadas no mesmo corpo. Logo, elas não se equilibram porque estão aplicadas em corpos diferentes. FN: Força Normal (perpendicular à superfície de contato) Capítulo 5 – Forças em Dinâmica Exercícios 1 – Na figura a seguir, temos uma maçã sobre uma mesa. a) Represente todas as forças que agem sobre a maçã. b) Onde estão aplicadas as correspondentes reações? fio que liga A e B é ideal, isto é, de massa desprezível e inextensível. A força horizontal F tem intensidade igual a 12N, constante. Determine: a) A aceleração do sistema; b) A intensidade da força de tração do fio. 3
5 – No arranjo experimental da figura, os corpos A, B e C têm, respectivamente, massas iguais a mA=5kg, mB=2kg e mC=3kg. A aceleração da gravidade é 10m/2. Os fios são inextensíveis e de inércia desprezível; não há atrito entre os fios e as polias; o plano horizontal é perfeitamente liso. Determine: a) A aceleração do sistema de corpos; b) As trações nos fios. 2 – Dois blocos A e B, de massas respectivamente iguais a 2kg e 3kg, estão apoiados numa superfície horizontal perfeitamente lisa. Uma força horizontal F, de intensidade constante F=10N, é aplicada no bloco A. Determine: a) A aceleração adquirida pelo conjunto; b) A intensidade da força que A aplica em B. 6 – No arranjo experimental da figura, os corpos A e B têm, respectivamente, massas iguais a 6kg e 2kg. Os fios e polias têm massas desprezíveis. Não há atrito entre o fio e a polia. Adote g=10m/s2. Determine: a) A aceleração do conjunto; b) As trações nos fios. Considere que o sistema partiu do repouso. 3 – Três corpos A, B e C de massas mA=1kg, mB=3kg e mC=6kg estão apoiados numa superfície horizontal perfeitamente lisa. A força horizontal F, de intensidade constante F=5N, é aplicada ao primeiro bloco A. Determine: a) A aceleração adquirida pelo conjunto; b) A intensidade da força que A exerce em B; c) A intensidade da força que B exerce em C. 4 – Dois corpos A e B de massas iguais a mA=2kg e mB=4kg estão apoiados numa superfície horizontal perfeitamente lisa. O Capítulo 5 – Forças em Dinâmica 7 – Determine a força que o homem deve exercer no fio para manter em equilíbrio estático o corpo suspenso de 120N. Os fios são considerados inextensíveis e de massas desprezíveis; entre os fios e as polias não há atrito. As polias são ideais, isto é, não têm peso. Atrito estático A máxima intensidade da força de atrito estático, e que corresponde à iminência de movimento, é dada por: f at ( máx ) = µe .FN 4
4 – Forças de atrito Atrito dinâmico Força de resistência oposta ao movimento relativo dos corpos: força de atrito dinâmico. Rugosidade da superfície e forças de adesão entre as moléculas. A intensidade da força de atrito é proporcional à intensidade da força normal FN: f at = µ d .FN Onde a constante de proporcionalidade é chamada de coeficiente de atrito dinâmico. Só há movimento quando F > f at ( máx ) Experimentalmente verifica‐se que a intensidade da força de atrito dinâmico é menor que a intensidade da força de atrito estático máxima. Capítulo 5 – Forças em Dinâmica 5 – Resistência do ar R=k.V2 K: •
Exercícios 1 – Dois corpos A e B de massas 1kg e 2kg estão ligados por uma corda de peso desprezível, que passa sem atrito pela polia C. Entre A e o apoio existe atrito de coeficiente µ d =0,5. Adote g=10m/s2. Determine: a) A aceleração dos corpos; b) A tração do fio. 2 – O bloco A de massa m=3kg está apoiado num plano inclinado que forma um ângulo θ em relação à horizontal. O bloco A está na iminência de escorregar para baixo. Determine, nessas condições, o peso do bloco B. O coeficiente de atrito estático entre o bloco A e o plano é µe =0,50. Considere o fio e a polia ideais. (dados: senθ=0,60; cosθ=0,80; g=10m/s2) Forma do corpo (coeficiente de arrasto aerodinâmico Cx) (veículos – entre 0,3 e 0,9) (gota de chuva – 0,05) • Maior área da seção transversal do corpo perpendicular à direção do movimento. • Densidade do ar. k=(d.A.Cx)/2 então R=
1
d . A.Cx .v 2 2
Velocidade limite em quedas Exercícios 1 – Um homem e seu pára‐quedas têm massa total de 100kg. A força resistência do ar têm intensidade: R=k.v2, sendo k=40Ns2/m2. Adote g=10m/s2 e determine a velocidade limite de queda. 2 – Um automóvel de massa total 1000kg desloca‐se num trecho retilíneo. A força máxima que o motor do carro pode exercer é 1800N. Admita que as forças de resistência ao movimento do carro se reduzam praticamente à resistência do ar R, dada por R=1,5v2, sendo v a velocidade do carro medida em metros por segundo e R em Newtons. Calcule a velocidade limite do automóvel nessas condições. 5