UNIVERSIDADE DO VALE DO ITAJAÍ
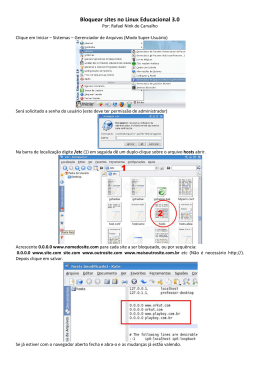
CENTRO DE CIÊNCIAS TECNOLÓGICAS DA TERRA E DO MAR
CURSO DE CIÊNCIA DA COMPUTAÇÃO
ESTUDO DE RESOLUÇÃO DO CLIQUE MÁXIMO
ATRAVÉS DE OPEN MPI
por
Jéferson Fernandes da Silva
Itajaí (SC), Dezembro de 2013
UNIVERSIDADE DO VALE DO ITAJAÍ
CENTRO DE CIÊNCIAS TECNOLÓGICAS DA TERRA E DO MAR
CURSO DE CIÊNCIA DA COMPUTAÇÃO
ESTUDO DE RESOLUÇÃO DO CLIQUE MÁXIMO
ATRAVÉS DE OPEN MPI
Área de Algoritmos
por
Jéferson Fernandes da Silva
Relatório apresentado à Banca Examinadora
do Trabalho Técnico-científico de Conclusão
do Curso de Ciência da Computação para
análise e aprovação.
Orientador: Rafael de Santiago, M.Sc.
Itajaí (SC), Dezembro de 2013
À minha família e especialmente à Nildo Carlos da Silva, meu querido pai.
AGRADECIMENTOS
Agradeço a Deus, por todos os momentos que foram superados e que me fizeram
aprender mais sobre a vida.
A minha família, mãe, pai, irmãos, por sempre estarem presentes em minhas escolhas
e me ensinarem a ser sempre uma pessoa melhor.
A minha companheira, Micaelly de Oliveira Mesquita, pela compreensão, carinho,
reflexões e conselhos.
A todos os professores que me acompanharam nesses anos, que passaram um pouco de
seu conhecimento, motivações e visões do mundo ao qual estou sempre sendo preparado.
Ao Rafael de Santiago, professor e orientador, por ter proporcionado diversos
momentos de aprendizado, dentro e fora de sala de aula, auxiliando e proporcionando esta
oportunidade.
“A tarefa não é tanto ver o que ninguém viu ainda, mas pensar o que ninguém pensou sobre
algo que todos vêem”
– Arthur Schopenhauer.
RESUMO
SILVA, Jéferson Fernandes da. Estudo de Estratégia para Abordar Programação Paralela
Open MPI em Problemas NP-Completo. Itajaí, 2013. 62 folhas. Trabalho Técnicocientífico de Conclusão de Curso (Graduação em Ciência da Computação) – Centro de
Ciências Tecnológicas da Terra e do Mar, Universidade do Vale do Itajaí, Itajaí, 2013.
Os problemas NP-Completo estão relacionados a problemas de otimização como alocação de
recursos, detecção e correção de erros em comunicação digital, genética, transporte e
logística. Estes problemas são conhecidos por sua complexidade computacional exponencial,
o que os define como intratáveis para tamanhos consideráveis de entrada. Para que estes
problemas possam ser resolvidos em tempo razoável, podem ser utilizadas várias técnicas
encontradas na computação, tais como: Algoritmos Aproximados, Heurísticas, Programação
Paralela, entre outros. O projeto tem o objetivo de analisar o desempenho do problema NPCompleto Clique Máximo, executando-o sequencialmente, paralelamente na mesma máquina
com threads e em mais de uma máquina com threads, nestes últimos utilizando a tecnologia
livre Open MPI. O trabalho é fundamentado em livros, pesquisas acadêmicas e artigos
científicos, que possibilitaram aprimorar os conceitos pertinentes ao problema NP-Completo e
as estratégias abordadas por diversos autores na busca da resolução mais eficiente possível
dos problemas desta classe. O desenvolvimento do TTC2 iniciou com as codificações dos
algoritmos sequencial e paralelo, para que pudessem ser executados visando efetuar a coleta
dos dados a partir de quatro execuções em cada ambiente heterogêneo, onde se obteve a
média e os resultados analisados comparativamente, possibilitando posicionar as estratégias
abordadas neste trabalho e a tecnologia livre Open MPI. A estratégia abordada foi baseada na
utilizada por Pardalos et al. (1997) e tem como objetivo enviar vértices do grafo para que as
threads destinadas ao processamento possam obter os cliques que aquele vértice pertence, em
múltiplas máquinas em um ambiente de rede. Através dos resultados obtidos é possível
observar que para mais densos o paralelismo é justificável, assim destes resultados é
importante destacar que as melhoras obtidas são de mais de 2 vezes com relação a
programação sequencial.
Palavras-chave: NP-Completo. Computação Paralela. Open MPI.
ABSTRACT
The problems are NP -complete optimization problems related to resource allocation,
detecting and correcting errors in digital communication, genetics, transportation and
logistics. These problems are known for their exponential computational complexity, which
defines them as intractable for sizeable input. Approximate Algorithms, Heuristics, Parallel
Programming, among others: that these problems can be solved in reasonable time, various
techniques found in computing, such as may be used. The project aims to analyze the
performance of NP- Complete Click Maximum running it sequentially, in parallel on the same
machine with threads and on more than one machine with threads in recent technology using
the free Open MPI. The work is based on books, academic research and scientific articles,
which enabled enhance relevant to the problem NP-Complete concepts and strategies
discussed by several authors in search of the most efficient possible resolution of the
problems of this class. The development of TTC2 began with the encodings of sequential and
parallel algorithms, so they could be executed aiming perform data collection from four plays
in each heterogeneous environment, where it averaged and compared the results analyzed,
enabling positioning strategies addressed in this work and the free Open MPI technology. The
strategy was based on the addressed used by Pardalos et al. (1997 ) and aims to send vertices
of the graph so that the intended processing threads can get the clicks that vertex belongs, on
multiple machines in a network environment. Through the results, we observe that for denser
parallelism is justifiable, so these results it is important to note that the improvements
obtained are more than 2 times compared with the sequential programming.
Keywords: NP-Complete. Parallel Computing. Open MPI.
LISTA DE FIGURAS
Figura 1.
Figura 2.
Figura 3.
Figura 4.
Figura 5.
Figura 6.
Figura 7.
Figura 8.
Figura 9.
Figura 10.
Figura 11.
Figura 12.
Figura 13.
Figura 14.
Figura 15.
Figura 16.
Figura 17.
Figura 18.
Algoritmo Determinístico e Não-determinístico .................................................... 19
Descrição tentativa do mundo NP .......................................................................... 20
Redução Polinomial ............................................................................................... 21
Redução do ciclo Hamilton para o problema do Caxeiro-Viajante ........................ 22
Árvore de backtracking .......................................................................................... 23
Um grafo com 4-Clique .......................................................................................... 24
Um grafo com Clique Máximo .............................................................................. 25
Multicomputadores interconectados ....................................................................... 29
Classes que compõem o Open MPI ........................................................................ 31
Resultados da execução do clique do grafo .......................................................... 35
Grafo exemplo e os conjuntos V, A e B ............................................................... 39
Árvore de backtracking ........................................................................................ 40
Arquitetura em múltiplos computadores .............................................................. 41
Divisão do grafo em subgrafos ............................................................................. 42
Árvore de backtracking paralela ........................................................................... 43
Resultados obtidos nos grafos menos densos. ...................................................... 47
Resultados obtidos nos grafos mais densos. ......................................................... 48
Resultados obtidos nos grafos dos grafos com densidades diferentes. ................ 48
LISTA DE TABELAS
Tabela 1. Equivalência de tipos de dados .............................................................................. 33
Tabela 2. Grafos DIMACS utilizados nas execuções para coleta dos dados. ....................... 45
Tabela 3. Grafos com a mesma quantidade de vértices e densidades diferentes. .................. 45
LISTA DE QUADROS
Quadro 1.
Quadro 2.
Quadro 3.
Quadro 4.
Quadro 5.
Quadro 6.
Quadro 7.
Quadro 8.
Quadro 9.
Quadro 10.
Estrutura do código MPI em C ............................................................................. 32
Código Hello World em Open MPI. ..................................................................... 33
Logica MaxClique ................................................................................................ 38
Resultados da execução sequencial do Clique Máximo. ...................................... 45
Resultados da execução do Clique Máximo com múltiplas threads. ................... 46
Comparativo entre as execuções do Clique Máximo............................................ 46
Clique Máximo – Função MaxClique .................................................................. 55
Clique Máximo – Bloco Main .............................................................................. 57
Clique Máximo – Função MaxCliqueMaster ....................................................... 60
Clique Máximo – Função MaxCliqueSlave........................................................ 61
LISTA DE ABREVIATURAS E SIGLAS
C++
CAM
CAMHAM
CD
CPU
CUDA
DIMACS
DVD
E/S
GCC
GPU
MIMD
MPI
MISD
NP
OMPI
OPAL
OPEN MPI
ORTE
P
SAT
SIMD
SISD
TTC
UNIVALI
C Plus Plus
Problema do Caminho
Problema do Caminho Hamiltoniano
Compact Disc
Central Processing Unit
Compute Unified Device Architecture
Center for Discrete Mathematics and Theoretical Computer Science
Digital Versatile Disc
Entrada/Saida
GNU Compiler Collection
Graphics Processing Unit
Multiple Instruction, Multiple Data
Message Passing Interface
Multiple Instruction, Single Data
Non-Deterministic Polynomial Time
Open Source Message Passing Interface Layer
Open Source Message Passing Interface Portable Access Layer
Open Source Message Passing Interface
Open Source Message Passing Interface Run-Time Enviroment
Deterministic Polynomial Time
Satisfazibilidade
Single Instruction, Multiple Data
Single Instruction, Single Data
Trabalho Técnico-científico de Conclusão de Curso
Universidade do Vale do Itajaí
SUMÁRIO
1 INTRODUÇÃO ................................................................................................................... 12
1.1 PROBLEMATIZAÇÃO..................................................................................................... 14
1.1.1 Formulação do Problema ............................................................................................. 14
1.1.2 Solução Proposta .......................................................................................................... 14
1.2 OBJETIVOS ..................................................................................................................... 14
1.2.1 Objetivo Geral .............................................................................................................. 14
1.2.2 Objetivos Específicos .................................................................................................... 15
1.3 METODOLOGIA ............................................................................................................. 15
2 FUNDAMENTAÇÃO TEÓRICA ...................................................................................... 17
2.1 TEORIA DA COMPLEXIDADE ...................................................................................... 17
2.1.1 Classe P ........................................................................................................................ 19
2.1.2 Classe NP ...................................................................................................................... 20
2.1.3 Classe NP-Completo ..................................................................................................... 20
2.1.4 Técnica Branch & Bound ............................................................................................. 22
2.2 PROBLEMA CLIQUE ..................................................................................................... 24
2.2.1 Heuristicas .................................................................................................................... 25
2.2.2 Programação paralela .................................................................................................. 26
2.2.3 Estrutura de um código MPI ........................................................................................ 31
2.3 TRABALHOS SIMILARES ............................................................................................... 34
2.3.1 Analise Comparativa de Algoritmos NP-Completo Executados em CPU e GPU
Utilizando CUDA ..................................................................................................................... 34
2.3.2 An Exact Parallel Algorithm For The Maximum Clique Problem ............................... 35
2.3.3 Comparativo e Considerações ...................................................................................... 36
3 DESENVOLVIMENTO ..................................................................................................... 37
3.1 ALGORITMO EXATO ..................................................................................................... 37
3.1.1 Clique Máximo .............................................................................................................. 37
3.2 ALGORITMO PARALELO .............................................................................................. 40
3.3 TESTE E RESULTADOS ................................................................................................. 43
3.3.1 Ambiente de Testes ........................................................................................................ 43
3.3.2 Resultados ..................................................................................................................... 45
4 CONCLUSÕES ................................................................................................................... 49
APÊNDICE A. ALGORITMO SEQUENCIAL ................................................................... 55
A.1 CLIQUE MÁXIMO .......................................................................................................... 55
APÊNDICE B. ALGORITMO PARALELO ....................................................................... 57
B.1 BLOCO MAIN ................................................................................................................. 57
B.2 CLIQUE MÁXIMO MASTER .......................................................................................... 60
B.3 CLIQUE MÁXIMO SLAVE ............................................................................................. 61
12
1 INTRODUÇÃO
Existem problemas computacionais que são classificados como "fáceis" ou "difíceis".
Esta classificação é obtida através da análise da complexidade dos algoritmos mais eficientes
para um determinado problema. A partir de uma análise matemática, extrai-se a complexidade
que é representada através de uma função. Se a função for polinomial, significa que o
problema pode ser resolvido demandando certa quantidade de recursos (tempo ou espaço) em
relação ao volume de entrada. Nestes casos classifica-se o problema como sendo fácil. Caso a
função seja exponencial, o problema demandará recursos exponenciais em relação à entrada,
caracterizando o problema como difícil (SIPSER, 2007).
Neste contexto existem duas classes de complexidade importantes para o estudo de
computação: a Classe P, composta por problemas que podem ser resolvidos em tempo
polinomial determinístico, a Classe NP (Polinomial Não-Determinístico) onde os problemas
podem ser resolvidos por um algoritmo não determinístico em tempo polinomial e pode ser
verificados em tempo polinomial (TOSCANI; VELOSO, 2005; SIPSER, 2007). Para a
Ciência da Computação teórica e matemática contemporânea à questão "P = NP" é um dos
maiores problemas não resolvidos. Caso essas classes sejam iguais, qualquer problema
polinomialmente verificável seria polinomialmente decidível (SIPSER, 2007).
De acordo com Arora e Barak (2009), os problemas da classe NP-Completo possuem
complexidade exponencial determinística, pertencem também à classe NP e podem ser
reduzidos polinomialmente a todos os problemas da mesma. São exemplos de problemas
desta classe: Cobertura de Vértices, K-Coloração, Clique do grafo, Caminho Hamiltoniano,
Caixeiro Viajante, Substituição de Expressões Regulares, Chave de Cardinalidade Mínima,
Escalonamento em Multiprocessadores, entre outros (GAREY; JOHNSON, 1979).
Este trabalho abordará o problema NP-Completo Clique Máximo, este consiste do
problema Clique que é um grafo composto por um conjunto de vértices no qual possuem
conexões mútuas, assim Clique Máximo é determinar o máximo de vértices que possuem
conexões mútuas (ZIVIANI, 2011).
Problemas NP-Completo são facilmente encontrados e estão relacionados a problemas
de otimização: em alocação de recursos, detecção e correção de erros em comunicação digital,
genética, transporte e logística (PAPADIMITRIOU;STEIGLITZ, 1998). Para que estes
13
problemas possam ser resolvidos em tempo razoável, podem ser utilizadas várias técnicas
encontradas na Computação: Algoritmos Aproximados, Heurísticas, Programação Paralela
entre outros (ZIVIANI, 2011).
A Programação Paralela surgiu para aumentar a disponibilidade, aproveitando a
evolução tecnológica e o baixo preço do hardware (STALLINGS, 2010). Uma das abordagens
deste tipo de programação é usar múltiplos processadores em paralelo, visando dividir a carga
de trabalho. Organizações mais comuns de múltiplos processadores em paralelo são:
Multiprocessadores Simétricos (SMP, do inglês Symmetric Multiprocessor), Clusters e o
Sistema de Acesso não Uniforme à Memória (NUMA, do inglês Nonuniform Memory Acess)
(STALLINGS, 2010).
A organização SMP é a interligação de um grupo de processadores semelhantes no
mesmo computador interligados por barramento ou por algum método de comutação, a
organização Cluster é a interligação de um grupo de computadores com recursos próprios e
trabalhando de forma unificada, já a organização NUMA utiliza o conceito de Cluster e em
cada nó (ou seja, cada maquina) utiliza o conceito de SMP, com o recurso de todos os
processos terem acesso a todas as partes da memória principal podendo efetuar operações de
leituras e escritas (STALLINGS, 2010).
A tecnologia MPI é uma interface entre aplicativo e programação (API) padronizada
utilizada para programação paralela e/ou computação distribuída. É constituída de duas
versões, a MPI-1(de 1994) e a MPI-2(de 1996), onde a MPI-2 é uma versão composta pela
primeira e mais recursos. A tecnologia livre Open MPI é um projeto de tecnologia MPI (do
inglês, Message Passing Interface), open source, desenvolvido e mantido por um consórcio de
ensino, pesquisadores e pessoas ligadas à indústria (OPENMPI, 2013).
O trabalho sugerido nesta proposta tem o objetivo de analisar o desempenho de dois
problemas NP-Completo ao serem executados sequencialmente em um processador e
paralelamente em múltiplos processadores, utilizando a tecnologia livre Open MPI. Neste
contexto, pretende-se responder a seguinte pergunta de pesquisa:
Como utilizar a tecnologia livre Open MPI para resolver problemas NP-Completo, de
modo a reduzir o tempo de execução em relação às tecnologias sequenciais?
14
Primeiramente foi efetuado o levantamento do material destinado ao aprofundamento
nos conceitos abordados no desenvolvimento do trabalho, assim foi pesquisado os Problemas
NP-Completo com o objetivo de observar (conhecer) cada particularidade envolvida e as
abordagens conhecidas, aprimorando os conceitos e possibilitando a realização da pesquisa de
implementação dos algoritmos sequenciais e paralelos e também foi pesquisado os conceitos e
tecnologias para possibilitar o pleno desenvolvimento utilizando a tecnologia livre Open MPI.
Assim concluídas foi possível executar os algoritmos e coletar as informações necessárias
para efetuar os comparativos.
1.1 PROBLEMATIZAÇÃO
1.1.1 Formulação do Problema
Posicionar problemas NP-Completo utilizando dois paradigmas da computação, a
programação Sequencial e a programação Paralela, buscando melhor aplicar as técnicas
conhecidas e obter resultados significativos para que se possa encontrar a resolução destes
problemas em tempo polinomial.
Como a tecnologia livre Open MPI alcança alto desempenho os problemas da classe
NP-Completo podem ser analisados visando bons resultados.
1.1.2 Solução Proposta
Para solucionar o problema proposto serão codificados algoritmos para programação
sequencial para CPU e programação paralela para múltiplas threads e múltiplos computadores
com múltiplas threads, utilizando a tecnologia livre Open MPI. Os resultados obtidos serão
analisados comparativamente visando posicionar a tecnologia livre Open MPI na resolução
dos problemas NP-Completo.
1.2 OBJETIVOS
1.2.1 Objetivo Geral
Identificar estratégias para abordar o problema do Clique Máximo em Programação
Paralela utilizando a tecnologia livre Open MPI.
15
1.2.2 Objetivos Específicos
Os objetivos específicos deste projeto de pesquisa são:
•
Levantar algoritmo para o Clique Máximo;
•
Codificar o algoritmo sequencial;
•
Codificar o algoritmo paralelo;
•
Coletar e analisar os dados de forma comparativa e posicionar a perspectiva paralela
utilizada;
•
Indicar os potenciais da Programação Paralela com relação à Programação Sequencial
aplicada ao problema do Clique Máximo.
1.3 METODOLOGIA
Este trabalho foi divido em seis etapas: (i) levantamento de material para
fundamentação teórica; (ii) codificação do algoritmo sequencial; (iii) codificação do
algoritmo paralelo; (iv) execução e coleta de dados; (v) análise dos resultados dos
experimentos; (vi) documentação do TTC.
Na primeira etapa, foram pesquisadas e conceituadas todas as informações necessárias
para a realização deste projeto, nas áreas de teoria da complexidade, problemas NP-Completo,
programação paralela e tecnologia livre Open MPI. As informações foram extraídas
principalmente em trabalhos de conclusão, dissertações de mestrados, livros e artigos.
Na segunda etapa, foi analisada a lógica do algoritmo, onde o mesmo foi codificado e
documentado.
Na terceira etapa, que foi realizada no TCC II, foi codificado o algoritmo em
programação paralela utilizando a tecnologia livre Open MPI baseando-se na fundamentação
e nos trabalhos similares.
Na quarta e quinta etapa, foi realizada a coleta dos dados com base nas execuções dos
algoritmos e a analise dos resultados utilizando de uma metodologia comparativa visando a
confiabilidade e possibilitando posicionar a tecnologia livre Open MPI.
16
Na última etapa, foi realizada a documentação do TCC I e TCC II, onde são descritos
a fundamentação, codificação dos algoritmos, dados coletados das execuções e análises de
resultados obtidos.
17
2 FUNDAMENTAÇÃO TEÓRICA
A Fundamentação Teórica realiza um levantamento de conceitos importantes
relacionais ao projeto deste TTC. Os tópicos a serem destacados são: Classes de
Complexidade, Problema NP-Completo Clique Máximo, Programação Paralela e tecnologia
livre Open MPI.
2.1 TEORIA DA COMPLEXIDADE
A Teoria da Complexidade estuda a razão de problemas computacionais quanto a sua
dificuldade, computacionalmente difíceis ou fáceis e quais destes problemas estão
relacionados quanto ao consumo de recurso (SIPSER, 2005).
Um problema computacional é aquele que se pode obter uma solução de acordo com
uma determinada entrada. Solução é o que satisfaz a relação com entrada utilizada. Podemos
utilizar como exemplo o problema de ordenação, onde a entrada é uma lista preenchida com
elementos aleatórios e como solução é gerada uma sequência ordenada de seus elementos
(NIKOLAY, 2013).
Problemas computacionais são medidos de acordo com a utilização de tempo e/ou
memória. Segundo Cook (1983) a complexidade de tempo é a medida de complexidade mais
importante, pois as pesquisas realizadas são fortemente direcionadas para projetar e analisar
algoritmos quanto a sua eficiência. O algoritmo que fornece a solução mais rápida é
considerado o mais eficiente (GAREY; JOHNSON, 1979).
Para mensurar a complexidade de tempo de um algoritmo é preferível evitar a medida
empírica, esta é fortemente dependente da programação e da maquina utilizada para
implementar o algoritmo, de maneira que se dois programas são comparados em duas
maquinas os resultados poderão ser diferentes devido as características das máquinas serem
diferentes. A alternativa para a medida empírica é a utilização de cálculos matemáticos para
analisar as dificuldades intrínsecas na resolução do problema (TOSCANI; VELOSO, 2005).
Segundo Toscani e Veloso(2005) para medir a quantidade de trabalho despendido por
um algoritmo, é escolhido uma operação, denominada operação fundamental, está somente é
aceitável se o número de operações executadas pelo algoritmo é proporcional ao número de
execuções da operação fundamental.
18
Segundo Toscani e Veloso (2012) o esforço de um algoritmo sobre uma dada entrada,
considerando a sequencia de passos executados pelo algoritmo e a quantidade de vezes que
são executadas as operações fundamentais pode-se descrever pela formula:
→ → ⋯ → → ⋯ → Equação 1
Um problema computacional pode ser resolvido por vários algoritmos. Logo, para
classificá-lo de acordo com uma função de complexidade, considera-se o algoritmo conhecido
mais eficiente para resolvê-lo (TOSCANI; VELOSO, 2012).
Dada complexidades dos problemas computacionais, existe um sistema de
classificação, chamado de Classes de complexidade, que são conjuntos de problemas que
podem ser decididos dentro de um mesmo recurso computacional (ARORA; BARAK, 2009).
Em relação ao recurso computacional requerido, as três classes de complexidade envolvidas
no contexto deste trabalho são: P, NP e NP-Completo.
Para compreender as classes de complexidade, os conceitos de algoritmos
determinísticos e não determinísticos são fundamentais: (i) algoritmos determinísticos são
aqueles que o resultado de cada operação é obtido unicamente; e (ii) algoritmos não
determinísticos são aqueles que o resultado não é unicamente definido, sendo capaz de
escolher uma dentre as alternativas possíveis a cada passo. Através de um dispositivo teórico
é possível execução de múltiplas configurações consumindo o tempo de apenas uma. A
Figura 1 ilustra as duas definições. (ZIVIANI, 2011).
19
Figura 1. Algoritmo Determinístico e Não-determinístico
Fonte: Adaptado Sipser (2007)
Nas subseções à seguir são conceituadas e exemplificadas as três classes de
complexidade mais relacionadas a este trabalho de conclusão: P, NP e NP-Completo.
2.1.1 Classe P
Segundo Ziviani (2011), a Classe de complexidade P (polynomial time) é o conjunto
formado de todos os problemas que podem ser resolvidos por algoritmos determinísticos em
tempo polinomial. Os algoritmos de tempo polinomial são considerados rápidos para muitos
propósitos e qualquer um pode simular outro com somente algum aumento polinomial no
tempo de execução (SIPSER, 2007; CARDOSO, 2012).
Segundo Sipser (2007), a classe P é importante por ser invariante a todos os modelos
polinomialmente equivalentes a Maquina de Turing determinística de uma única fita e por
corresponder aproximadamente à classe de problemas que são solúveis por um computador
em tempo aceitável.
Segundo Ziviani (2011), um problema da Pesquisa Sequencial consiste em percorrer
um conjunto de registros, do inicio até encontrar o que se procura, este conjunto que
armazenará os dados pode-se uma estrutura de arranjo que possui uma chave que identifica o
20
registro, assim caso encontre o registro que se procura é retornado à chave ou posição do
registro neste arranjo, caso contrario retorna o valor zero.
2.1.2 Classe NP
Segundo Ziviani (2011), a Classe de complexidade NP (Non-Deterministic Polynomial
Time) é o conjunto formado por todos os problemas que são solucionados por algoritmos não
determinísticos em tempo polinomial. Os problemas desta classe podem ser verificados
utilizando algoritmos determinísticos em tempo polinomial, segundo Sipser (2007) esta
característica é chamada de Verificabilidade polinomial e é importante para entender a
complexidade do problema.
Assim sendo, se P = NP, problemas que são resolvidos em tempo exponencial
poderiam ser resolvidos em tempo polinomial, o que resultaria em uma grande redução do
tempo de execução. Uma área na qual esta mudança seria importante é a Criptografia. Quando
um sistema de criptografia é criado, uma de suas premissas é que para que se possa quebrar a
segurança consumindo um tempo exponencial. Caso P = NP, os algoritmos de quebra de
criptografia poderiam ser executados mais rapidamente, consumindo segundos ou minutos, ao
invés de semanas, meses ou anos (SIPSER, 2007;ARORA; BARAK, 2009).
Figura 2. Descrição tentativa do mundo NP
Fonte: Adaptado de Ziviani (2011)
2.1.3 Classe NP-Completo
Segundo Ziviani (2011), Stephen Cook e Leonid Levin buscavam um problema NP
que pudesse ser resolvido utilizando um algoritmo polinomial determinista, de forma que
21
todos os problemas NP também pudessem ser resolvidos em tempo polinomial, assim
surgindo à questão P = NP, esta que busca saber se algum problema NP esta contido em P.
Segundo Ziviani (2011), para poder provar que um problema é NP-Completo é preciso
seguir alguns passos, como: (i) primeiramente provar que o problema é NP; (ii) e em seguida
mostrar que um problema NP-Completo pode ser transformado para o problema NP, através
da transformação polinomial.
Segundo Ziviani (2011, p. 413),
Considere II1 e II2 dois problemas “sim/não”, conforme mostrada na Figura
3. Suponha que exista um algoritmo A2 para resolver II2. Se for possível transformar
II1 em II2 e sendo conhecido um processo de transformar a solução de II2 em uma
solução de II1, então o algoritmo A2 pode ser utilizado para resolver II1. Se as
transformações nos dois sentidos puderem ser realizadas em tempo polinomial,
então II1 é polinomialmente transformável em II2.
Figura 3. Redução Polinomial
Fonte: Adaptado de Ziviani (2011)
Segundo Sipser(2007) para provar que um dado problema B é NP-Completo, verificase duas condições: (i) se B esta em NP; e (ii) se todo problema A em NP é polinomialmente
redutível a B.
Como exemplo será provado que o problema do caixeiro-viajante é NP-Completo a
partir do problema do ciclo de Hamilton, que é um dos primeiros problemas a ser provado
como NP-Completo (ZIVIANI, 2011).
Segundo Ziviani (2011) para provar que o problema do caixeiro-viajante é NPCompleto são realizados 2 passos, onde o primeiro consiste em mostrar que o problema está
em NP apresentando um algoritmo não determinista polinomial para o problema do caixeiro-
22
viajante ou a partir de uma solução dada efetuar a verificação em tempo polinomial, o
segundo passo consiste em apresentar uma redução polinomial para o problema do ciclo de
Hamilton para o problema do caixeiro-viajante. A redução polinomial pode ser efetuada como
na Figura 4, onde os vértices representam as cidades e as arestas as distancias, utilizando peso
1 para quando existe a aresta originalmente e o peso 2 para quando não existir.
Figura 4. Redução do ciclo Hamilton para o problema do Caxeiro-Viajante
Fonte: Adaptado de Ziviani (2011).
Em muitos casos, opta-se por utilizar uma solução heurística para problemas NPCompleto. Segundo ZIVIANI (2011), uma heurística é uma maneira de resolver um problema
computacional gerando uma solução, que pode ser ótima, ou seja, a resposta exata para o
problema, próxima ou distante da solução ideal (ótima). Geralmente, justifica-se o uso de uma
solução heurística para casos em que a obtenção da solução ótima demandaria tempo
exponencial. Com as heurísticas, relaxa-se a exigência de uma solução para um resultado
ideal, para uma resposta em tempo polinomial.
2.1.4 Técnica Branch & Bound
Segundo Ziviani (2011), a finalidade desta técnica é eliminar partes do problema que
não chegarão a uma solução melhor do que a já obtida. Por exemplo, em um problema de
“caminho”, a cada etapa (ou seja, cada vértice), é verificado o custo do caminho percorrido
até aquele ponto, assim se este custo for maior ou igual a um custo obtido então este caminho
é eliminado.
Branch & Bound é uma técnica utilizada para encontrar a solução de problemas
através da enumeração sistemática de possíveis soluções, assim o algoritmo tende a reduzir o
23
número de soluções geradas utilizando limitantes inferiores e superiores. A técnica consiste
em subdividir um problema em subproblemas menores (branching) e elimina os conjuntos de
subproblemas que podem não levar a uma solução ótima (bounding) (CARMO; ZÜGE,
2012).
O limitante superior é um valor estimado, maior ou igual ao valor de uma solução
ótima de um determinado subproblema e o limitante inferior pode ser uma estimativa ou a
melhor solução de algum subproblema (CARMO; ZÜGE, 2012).
O passo de branching é onde o problema é subdividido em subproblemas e pode ser
emprega a técnica de backtracking, que consiste em gerar sistematicamente todas as soluções
possíveis, na Figura 5 é ilustrada uma árvore de backtracking e o passo de bounding é onde
ocorre a eliminação do subproblema verificando o valor do limitante superior com o valor do
limitante inferior do problema global, assim caso o limitante maior seja menor que o limitante
inferior é efetuado a eliminação (CARMO; ZÜGE, 2012).
Figura 5. Árvore de backtracking
Fonte: Adaptado de Kreher e Stinson (1999).
Há uma grande busca por algoritmos cada vez mais eficientes, mesmo que não
polinomiais, devido ao Problema do Clique Máximo ser um dos problemas fundamentais. Na
literatura há diversos algoritmos e diversas abordagens para encontrar a solução exata, destas,
duas são consideradas clássicas, Branch & Bound e Lower Bound, a primeira por limites
24
superiores associada à técnica enumerativas e a segunda por limites inferiores através de
algoritmos de procura local (CARMO; ZÜGE, 2012; CAVIQUE; REGO; THEMIDO,2013).
A técnica de Branch & Bound é utilizada em vários algoritmos por diversos autores
em sua base, mas cada um difere utilizando abordagens diferentes para problemas diferentes,
buscando cada vez mais soluções otimizadas, alguns autores tratam de problemas do mundo
real enquanto outros tratam de problemas do mundo artificial. Podem-se citar algumas áreas,
tais como análise de mercado, seleção de projetos, teoria da transmissão de sinais, economia,
agendamentos, design experimental, visão computacional entre outros (CARMO; ZÜGE,
2012; CAVIQUE; REGO; THEMIDO,2013).
2.2 PROBLEMA CLIQUE
O Clique do Grafo é um problema comprovadamente NP-Completo por Richard Karp
em 1972, este possui a característica de que todos os vértices possuem conexões mútuas. O
problema do Clique possui algumas variações, tais como k-Clique, Clique Máximo e Clique
maximais. O k-Clique é um grafo que possui um tamanho especifico k, ilustrado na Figura 6
(SIPSER, 2007; ZIVIANI, 2011).
Figura 6.Um grafo com 4-Clique
Fonte: Adaptado de SIPSER (2007)
Outra variação do problema Clique é o “Clique Máximo” de um grafo, que consiste
em um clique com o maior número de vértices que possuem conexões mútuas, conforme
ilustrado na Figura 7.
25
Figura 7.Um grafo com Clique Máximo
Fonte: Adaptado de SIPSER (2007)
Uma das aplicações estudadas nos trabalhos similares é um modelo prático do
problema, aplicada na área de sistemas distribuídos, sendo esta utilizada em uma rede de
computadores espalhados e conectados por internet com a finalidade de testar as condições
adversas. O estudo tinha por finalidade encontrar conjuntos estáveis onde os vértices
representavam computadores e arestas representavam a conexão com determinada qualidade.
2.2.1 Heuristicas
As heurísticas são maneiras de resolver um dado problema computacional em casos
que para chegar a uma solução ideal demandaria de recursos (tempo ou espaço) exponencial,
assim as soluções podem ser ótimas, próximas ou distantes da solução ideal.
2.2.1.1
Hill-Climbing
O método de Subida de Encosta (Hill-Climbing) faz analogia à escalada de uma
colina, sugerindo que o caminho mais rápido para o topo de uma colina é mover-se de forma
contínua no sentido do valor crescente. A busca é efetuada visitando os vizinhos imediatos,
desta maneira nenhum vizinho terá o valor mais alto e só termina quando alcança o topo
(KREHER; STINSON, 1999).
26
2.2.1.2
Simulated Annealing
O Recozimento Simulado (Simulated Annealing) é um dos métodos análogo ao
processo físico de resfriamento de um metal, este processo consiste em reduzir a energia
interna do material cuidadosamente. A função objetivo corresponde ao nível de energia do
sistema, esta que se deseja minimizar. Este método utiliza da estratégia de busca na
vizinhança de forma semi-aleatória e de probabilidade de aceitação para novas soluções, onde
soluções que melhoram o valor da função objetivo são sempre aceitas e soluções que pioram o
valor da função objetivo são condicionalmente aceitas (KREHER; STINSON, 1999;
PEREIRA, 2004).
2.2.1.3
Algoritmos Genéticos
Algoritmos Genéticos (Genetic Algorithm) é um método análogo ao processo
evolutivo, onde os indivíduos representam a solução do problema, sendo assim, a seleção
natural é um critério de escolha das melhores soluções e a eliminação das ruins, o cruzamento
e a mutação são meios para a obtenção de novas soluções (LOPES, 1995; AGUIAR, 1998;
KREHER; STINSON, 1999).
2.2.2 Programação paralela
Desde a popularização do computador há uma demanda por computadores cada vez
mais eficientes, com maior poder computacional e de armazenamento para resolver diversos
problemas na ciência, engenharia e indústria. Alguns incentivos que intensificaram a
exploração do paralelismo pode-se destacar os avanços consideráveis na área de tecnologia e
a redução do custo do hardware (TANENBAUM, 2007; STALLINGS, 2010).
Segundo Tanenbaum (2007), a velocidade dos circuitos não pode aumentar
indefinidamente devido aos limites físicos, como a dissipação de calor e problemas que
podem surgir devido a redução do tamanho dos transistores. Na historia dos computadores
pode-se destacar que por algumas décadas o principal método de aumento do desempenho nas
CPUs(Central Proessing Units) é devido ao incremento da velocidade de operações por
segundo dos processadores, conhecido como Clock, partindo de poucas operações por
segundo até chegar em frequências entre 1GHz e 4Ghz em meados dos anos 2000, após isto
alguns limites físicos foram encontrados, tais como: (i) o alto consumo de energia dos
circuitos integrados; (ii) restrições de dissipação de calor; (iii) e limites na fabricação de
27
resistores ainda menores. Isto motivou arquitetos de computadores buscarem alternativas para
se ganhar desempenho (TANENBAUM, 2003).
Os arquitetos de computadores passaram a recorrer ao método paralelização de
processamento, seja em múltiplos computadores ou em múltiplas unidades de processamento.
O paralelismo pode ser introduzido em vários níveis, desde o mais baixo, que resultaria em
adicionar ao chip da CPU, sendo por meio de pipeline e projetos superescalares, por meio de
palavras de instrução, por meio de características para permitir que a CPU possua múltiplos
threads de controle e por meio de várias CPUs no mesmo chip. Em um nível seguinte pode-se
introduzir placas de CPUs extras ao sistema, estas com funções específicas tais como
processamento de pacotes de redes, multimídia e outros. O nível final envolve utilizar a
conexão de rede para interligar grades de computadores (TANENBAUM, 2007).
Nas seções seguintes tópicos importantes para o melhor entendimento da programação
paralela
serão
abordados,
tais
como
Taxonomia
de
Flynn,
multiprocessadores,
multicomputadores (ou múltiplos computadores) e sistemas distribuídos.
2.2.2.1
Taxonomia de Flynn
Segundo Stallings (2010), a Taxonomia de Flynn é ainda a maneira mais comum de
categorizar sistemas com capacidade de processamento paralelo. Esta classificação é baseada
em dois conceitos, fluxo de instruções e fluxo de dados, onde o fluxo de instruções
corresponde a uma sequência de instruções a ser executada por um computador e o fluxo de
dados consiste em uma sequência de dados a ser manipulados por um fluxo de controle. As
combinações do fluxo de instruções e fluxo de dados são divididas em SISD (single
instruction, single data), SIMD (single instruction, multiple data), MISD (multiple instruction,
single data), MIMD (multiple instruction, multiple data) (TANENBAUM, 2007;
STALLINGS, 2010).
•
SISD: É um sistema com um único fluxo de instruções que é executada por um
único processador para manipular os dados armazenados em uma única
memória, um único dado.
•
SIMD: É um sistema com um único fluxo de instruções que é executada em
vários conjuntos de dados simultaneamente.
28
•
MISD: É um sistema que executa múltiplas instruções em um mesmo dado,
pode-se considerar um dado transmitido para um conjunto de processadores
para ser executado por uma sequencia de instruções diferentes.
•
MIMD: É um sistema que executa múltiplas instruções em múltiplos dados,
pode-se considerar um conjunto de processadores que executam sequencias de
instruções diferentes simultaneamente para um conjunto de dados diferentes.
Os multiprocessadores e multicomputadores são considerados MIMD.
2.2.2.2
Múltiprocessadores
Segundo Tanenbaum (2003), um multiprocessador é um computador onde duas ou
mais CPUs compartilham acesso total a uma memoria RAM comum. Por exemplo, um
programa que esta executando em uma das CPUs pode enxergar e manipular qualquer espaço
de endereço da memoria virtual.
Segundo Stallings (2010), multiprocessadores é uma das abordagens para melhorar o
desempenho, de forma a executar operações em paralelo assim dividindo a carga de trabalho
e/ou até mesmo melhorar a disponibilidade. Podem ser divididos em Multiprocessadores
Simétricos (Symmetric Multiprocessor) e Sistema de Acesso não Uniforme à Memória
(Nonuniform Memory Access).
•
Multiprocessadores Simétricos: Segundo Stallings (2010) é uma arquitetura de
hardware computacional que consiste na interligação de um grupo de
processadores semelhantes no mesmo computador através de barramento ou
algum método de comutação. São características possuir dois ou mais
processadores semelhantes, compartilhar memória principal e os recursos de
entrada e saída, os processadores desempenham a mesma função e o sistema é
controlado por um sistema operacional integrado.
•
Sistema de Acesso não Uniforme à Memória: Segundo Stallings(2010) é um
conjunto de computadores com recursos próprios que são interligados,
semelhante ao Cluster e possui a característica de poder efetuar operações
utilizando todas as memórias dos computadores interligados, onde o tempo de
acesso à memória varia de acordo com a região onde esta a memória.
29
2.2.2.3
Múlticomputadores
Segundo Tanenbaum (2003), multicomputadores são CPUs fortemente acoplados que
não compartilham memória, assim todos os CPU tem sua própria memoria local. A Figura 8
ilustra multicomputadores interconectados. Estes normalmente compartilham de uma
interconexão de alta velocidade, podendo ou não possuir um disco rígido. São conhecidos por
uma variedade de nomes, como computadores cluster e Clusters of workstations (clusters de
estações de trabalho).
Figura 8. Multicomputadores interconectados
Fonte: Adaptado de Tanenbaum (2003).
Segundo Stallings (2010), cluster é um conjunto de computadores, estações de
trabalho, com recursos próprios que são interligados visando fornecer alto desempenho e
disponibilidade de forma unificada.
Os multicomputadores são interconectados pela interface de rede de várias formas,
estas são conhecidas como topologias de rede e pode ser switch, anel, grade, toro duplo, cubo
ou hipercubo, onde cada uma possui um papel importante na disponibilidade, controle de
dados, dimensionamento entre outras (TANENBAUM, 2003).
2.2.2.4
Sistemas Distribuidos
Segundo Tanenbaum (2003), os sistemas distribuídos são semelhantes aos
multicomputadores no quesito de não possuírem memoria compartilhada, porém as estações
30
de trabalho são completas com todos os periféricos e fracamente acopladas, normalmente
interligadas através da internet e podem estar espalhadas pelo mundo.
Uma vantagem dos computadores serem fracamente acoplados é que podem ser
utilizados por diversas aplicações, porém a desvantagem é que a programação para essas
aplicações é difícil devido à falta de um modelo de plataforma comum (TANENBAUM,
2003).
2.2.2.5
Open MPI
Segundo TANENBAUM (2007) a tecnologia MPI (Message-Passing-Interface) é
constituída de duas versões, a primeira denominada MPI-1, foi publicada no ano de 1994,
composta de todos os requisitos base necessários para o padrão de troca de mensagens e a
segunda versão, mais complexa e ampliada denominada MPI-2, foi publicada no ano de 1997.
A tecnologia Open MPI apesar de atender aos tipos de sistemas paralelos citados
anteriormente, porém há necessidade de compilar o código para arquiteturas diferentes
espera-se maior praticidade em multicomputadores, tendo em vista que estes são fortemente
acoplados e normalmente utilizam o mesmo sistema operacional (OPENMPI, 2013).
A MPI é constituída de quatro conceitos principais, estes são Comunicador, tipos de
dados de mensagens, operações de comunicação e topologias virtuais.
•
O Comunicador é um mecanismo que identifica o grupo de processos e o
domínio (contexto) a qual uma operação deve ser efetuada, assim evitando que
as mensagens não relacionadas interfiram umas nas outras.
•
As mensagens possuem tipos de dados que são suportados, como caracteres,
números inteiros, longos, normais e outros, também sendo possível construir
outros a partir destes.
•
As operações de comunicação são utilizadas para enviar e receber os dados,
definir modos, bloqueios e qual a forma de comunicação.
•
A topologia virtual são os caminhos de comunicação, de forma a organizar os
processos em árvore, anel, grade, toro ou outra.
A tecnologia livre Open MPI é um projeto de tecnologia MPI, open source,
desenvolvido e mantido por um consorcio de ensino, pesquisadores e pessoas ligadas à
31
indústria, com a finalidade de obter altas performances, combinando vários projetos MPI já
existentes objetivando uma única implementação MPI integrando as finalidades destes
projetos (NEVES, 2009; OPENMPI, 2013).
A arquitetura do Open MPI é composta por três classes componentes, combinadas
provem todas as suas funcionalidades, é ilustrada pela Figura 9. A camada OMPI (Open MPI
Layer) é a camada mais superior e provê a interface MPI para as aplicações. Mais abaixo esta
a camada ORTE (Open MPI Run-Time Enviroment) que provê um ambiente de execução
paralelo independente das capacidades do sistema. Logo abaixo, a terceira camada OPAL
(Open Portable Access Layer) provê uma maior portabilidade das camadas superiores
abstraindo peculiaridades especificas do sistema. Abaixo de todas as camadas está o sistema
operacional e os outros serviços necessários executando no local (GRAHAM; WOODALL;
SQUYRES, 2005; NEVES, 2009).
Figura 9. Classes que compõem o Open MPI
Fonte: OpenMPI (2013)
2.2.3 Estrutura de um código MPI
Em todos os arquivos que utilizarão os recursos do MPI é obrigatório a inclusão do
cabeçalho mpi.h, este contem todas as definições de funções e constantes necessárias durante
o desenvolvimento e compilação do programa. No corpo do código todas as chamadas para
funções e constantes do MPI devem ser feitas entre MPI_Init e MPI_Finalize, conforme o
Quadro 1 (NEVES, 2009).
32
Quadro 1. Estrutura do código MPI em C
#include <stdio.h>
#include <mpi.h>
int main(int argc, char *argv[]) {
MPI_Init(&argc, &argv);
Bloco de comandos e as instruções MPI
MPI_Finalize();
}
O MPI segue uma padronização que visa a fácil identificação de métodos e tipos que
compõem a API, desta forma todos os identificadores possuem o prefixo “MPI_”. Tipos e
constantes são expressas em letra maiúsculas e funções são expressas com a primeira letra
maiúscula e as demais em minúsculo, por exemplo, o tipo MPI_SHORT e MPI_Send,
respectivamente (OPENMPI, 2013).
É empregado um manipulador de erros próprio para o tratamento de exceções, assim
caso ocorra algum problema durante a execução a sinalização e as ações a serem tomadas é
responsabilidade da API (OPENMPI, 2013).
Para poder oferecer suporte a várias linguagens foi desenvolvida uma equivalência de
tipos de dados entre a API e as linguagens suportadas, a Tabela 1 ilustra a equivalência com a
linguagem C.
33
Tabela 1. Equivalência de tipos de dados
Tipo de Dados do MPI
Tipo de Dados do C
MPI_CHAR
signed char
MPI_SHORT
signed short int
MPI_INT
signed int
MPI_LONG
signed long int
MPI_UNSIGNED_CHAR
unsigned char
MPI_UNSIGNED_SHORT
unsigned short int
MPI_UNSIGNED
unsigned int
MPI_UNSIGNED_LONG
unsigned long int
MPI_FLOAT
Float
MPI_DOUBLE
Double
MPI_LONG_DOUBLE
MPI_LONG_DOUBLE long double
MPI_PACKED
MPI_BYTE
Fonte: OpenMPI(2013)
Um exemplo de uma implementação “Hello World” em linguagem C utilizando Open
MPI, pode ser visto no Quadro 2:
Quadro 2. Código Hello World em Open MPI.
#include <stdio.h>
#include <mpi.h>
int main(int argc, char *argv[]) {
int numprocs, rank, namelen;
char processor_name[MPI_MAX_PROCESSOR_NAME];
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &numprocs);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Get_processor_name(processor_name, &namelen);
printf("Processo %d em %s de %d\n", rank, processor_name, numprocs);
MPI_Finalize();
}
Fonte: OpenMPI (2013)
34
2.3 TRABALHOS SIMILARES
Devido à complexidade computacional dos problemas NP-Completo, cientistas e
estudiosos buscam por utilizar técnicas conhecidas, adaptando-as e até unindo-as, visando
encontrar a solução para os problemas NP-Completo ou a melhor solução possível, e
consequentemente tendem a explorar formas de aumentar o desempenho através de
algoritmos paralelos.
A seguir é apresentado dois estudos no campo da programação paralela, o primeiro
Analise Comparativa de Algoritmos NP-Completo Executados em CPU e GPU Utilizando
CUDA e An Exact Parallel Algorithm for the Maximum Clique Problem (Um Algoritmo
Paralelo Exato para o Problema do Clique Máximo).
2.3.1 Analise Comparativa de Algoritmos NP-Completo Executados em
CPU e GPU Utilizando CUDA
Desenvolvido por Elcio Cardoso na Universidade do Vale do Itajaí em 2012, este teve
como objetivo comparar a execução de dois problemas NP-Completo, Clique Máximo e
Cobertura Mínima de um grafo, em duas arquiteturas diferentes, primeiramente em CPU e
posteriormente em GPU, utilizando da tecnologia CUDA.
O problema do Clique Máximo tem como objetivo encontrar o conjunto de vértices
que possui o maior número de conexões mutuas, ou seja, o clique de tamanho máximo em um
dado grafo, e o problema da Cobertura Mínima de um grafo tem como objetivo encontrar o
conjunto que possui o menor número de vértices que possuem pelo menos uma das pontas de
cada aresta (CARDOSO, 2012).
Os algoritmos foram executados e comparados em três ambientes, no primeiro foi
usando uma CPU com dois núcleos rodando a 2,4 GHz e os algoritmos desenvolvidos de
forma sequencial, no segundo ambiente, uma GPU Nvidia GeForce GT 640 com 384 núcleos
CUDA e no terceiro uma GPU Nvidia GeForce GTX 670 com 1344 núcleos CUDA, onde no
segundo e no terceiro foi utilizado algoritmos desenvolvidos para buscar o maior desempenho
paralelo que esta arquitetura pode oferecer (CARDOSO, 2012).
A Figura 10 apresenta a comparação entre as implementações para a CPU e GPUs,
ilustrando o tempo de execução obtido nos três ambientes, sendo que nos ambientes que
35
utilizam GPU houve a paralização de operações e a divisão em subgrafos. A execução foi
dada com as mesmas configurações e dados dos problemas, onde os problemas continham
quantidade de vértices diferentes e tamanho do clique diferentes, e os dados foram extraídos
da média de cinco execuções em cada ambiente (CARDOSO, 2012).
Figura 10. Resultados da execução do clique do grafo
Fonte: Cardoso (2012)
O autor concluiu que quando os grafos são menores a CPU apresenta vantagem sobre
a GPU do ambiente 2 devido o volume de dados a ser processados ser menor, e observou que
o mesmo não ocorre na GPU do ambiente 3 pois é mais eficiência neste tipo de operação.
Quando os grafos são maiores e consequentemente o volume de dados é maior, as GPUs
apresentam vantagem, pois quando o volume de dados aumenta o seu tempo de alocação
cresce proporcionalmente e a quantidade de processamento cresce exponencialmente.
2.3.2 An Exact Parallel Algorithm For The Maximum Clique Problem
Desenvolvido por Panos M. Pardalos, Jonas Rappe e Mauricio G. C. Resende e
apresentado na conferencia In High Performance and Software in Nonlinear Optimization em
1997, tem como objetivo apresentar um algoritmo paralelo exato portátil para o problema do
Clique Máximo em grafos gerais.
36
Os algoritmos foram executados e comparados em dois ambientes, no primeiro um
computador com 2 processadores e no segundo com 4 processadores, na implementação dos
algoritmos utilizou-se a linguagem Fortran 77. Os algoritmos foram testados em grafos
ponderados e não ponderados onde o tamanho variava de 64 vértices com 1.824 arestas até
500 vértices com 74.983 arestas (PARDALOS; RAPPE; RESENDE, 2013).
Os autores abordaram o problema utilizando a estratégia de Mestre-Escravo, esta
estratégia é composta por 2 programas, o programa Mestre e o programa Escravo, onde no
primeiro concentra o problema com os dados do conjunto de vértices, operações para dividir
em subgrafos e a solução dos subgrafos, no segundo, concentra o recebimento do subgrafo,
expansão do nó, o processamento e o envio da solução (PARDALOS; RAPPE; RESENDE,
2013).
Os autores concluíram com os resultados obtidos após vários testes que há um
aumento de performance, mais significativamente proporcional com o aumento de tamanho
(número de vértices e densidade) do problema.
2.3.3 Comparativo e Considerações
Os trabalhos similares utilizam da programação paralela para obter maior desempenho
na resolução dos problemas NP-Completo. Ambos os trabalhos utilizaram abordagens
diferentes devido à utilização de programação e arquiteturas diferentes, onde o primeiro
desenvolveu um algoritmo sequencial para tratar em uma CPU e também explorou estratégias
para a utilização da programação paralela em CUDA visando abordar os problemas NPCompleto clique máximo e cobertura de vértices, e o segundo desenvolveu estratégias para a
utilização de programação paralela em CPU, onde foi executado o algoritmo para o problema
do clique máximo, em máquinas com duas e quatro CPUs.
Este trabalho se difere do primeiro trabalho similar quanto à utilização da tecnologia
CUDA, esta utilizada na implementação da abordagem em programação paralela, e se
assemelha na utilização da programação sequencial para o problema NP-Completo clique
máximo, possui maior semelhanças com o segundo trabalho, devido à abordagem da
programação paralela para CPU, o emprego da tecnologia MPI padrão e estratégias visando
resolver o problema do clique máximo.
37
3 DESENVOLVIMENTO
Serão apresentados tópicos importantes para o desenvolvimento do projeto, testes e
análises dos resultados, utilizando das informações obtidas na fundamentação teórica.
Primeiramente será codificado o algoritmo sequencial para posteriormente codificar o
algoritmo paralelo, tendo em vista analisar a complexidade envolvida e efetuar a analise dos
resultados obtidos.
3.1 ALGORITMO EXATO
Inicialmente o algoritmo para o Clique foi desenvolvido e explorado para ser utilizado
em programação sequencial, a seguir será abordado o processo de implementação e análise da
complexidade dos problemas.
3.1.1 Clique Máximo
O problema do Clique Máximo pode ser resolvido utilizando a técnica de
recursividade, onde é percorrido o grafo em busca da solução, no Quadro 3 é apresentado a
lógica utilizada e a função recursiva MaxClique (KREHER; STINSON, 1999). A função
utiliza o seguinte conjunto de dados:
•
V: Vértices do Grafo;
•
A: Adjaventes de V;
•
B: Vértices a serem analisados;
•
C: Vértices que compõem a árvore de backtracking;
•
OptClique: Solução do problema;
•
l: Nível da árvore de backtracking.
O algoritmo proposto consiste em percorrer o grafo com base em sua árvore de
backtracking utilizando as relações entre vértices já verificadas no conjunto B e identificando
os possíveis adjacentes a serem incluídos no clique anterior encontrado.
São realizados pelo algoritmo descrito no Quadro 3 os seguintes passos:
38
•
Verifica-se a quantidade de vértices com ligações simultâneas da solução atual e caso
seja superior a solução encontrada, esta então é mantida (até que não reste maiores);
•
É criado um conjunto relativo às adjacências mutuas (conjunto C), ao grupo de
vértices analisados em questão;
•
Repetir os passos 1, 2 e 3 em cada adjacência mútuas identificas no passo 2, até que
não haja mais destas adjacências.
Quadro 3. Logica MaxClique
global A[l], B[l], C[l], x[l] (l = 0, 1, ... , n - 1)
MaxClique(l)
if l > OptSize {
OptSize <- l + 1
OptClique <- (x[0], ... , x[l-1])
}
if l == 0 {
C[l] <- V
} else {
C[l] <- A[x[l-1]] ∩ B[x[l-1]] ∩ C[l-1]
}
for each x2 ∈C[l]{
x[l] <- x2
MaxClique(l + 1)
}
main{
OptSize <- 0
MaxClique(0)
output(OptClique)
}
Fonte: Adaptado de Kreher e Stinson (1999).
Uma representação visual do grafo e os valores dos conjuntos V, A e B do MaxClique
pode ser visualizado a seguir na Figura 11.
39
Figura 11. Grafo exemplo e os conjuntos V, A e B
Fonte: Adaptado de Kreher e Stinson (1999).
O grafo utilizado na Figura 11 é composto de 5 cliques maximais e 21 cliques, para
obter o clique máximo é utilizado os conjuntos V, A e B, onde o primeiro é o conjunto de
todos os vértices do grafo, o segundo é o conjunto dos vértices adjacentes ao vértice que esta
sendo utilizado ( definido pela coluna V ) e o terceiro é o conjunto de todos os vértices
maiores que o vértice que esta sendo utilizado. O algoritmo tem como finalidade percorrer os
vértices do conjunto V utilizando o conjunto A para obter os vértices adjacentes, formando os
novos cliques a partir da verificação das conexões mutuas.
Simulando a execução caso o algoritmo iniciasse como elemento selecionado o 2 do
conjunto V, então é verificado o conjunto A para obter as adjacências 1, 3, 4 e 5, assim
obtém-se os elementos do conjunto B para efetuar a intersecção, obtendo como resultado os
elementos 3, 4 e 5, formando os conjuntos [2,3], [2,4], [2,5]. Como os cliques maximais estão
nos vértices 0 e 1, ao escolhermos o vértice 2 não encontraremos nenhum com o clique
máximo de 3 elementos, como o algoritmo é destinado a solução exata, deve ser executado
desde o vértice 0 pois este procedimento é efetuado desde o primeiro até o ultimo elemento do
conjunto V.
Na Figura 12 é ilustrada uma arvore de backtracking, tendo como elemento
selecionado o elemento 0 do conjunto V.
40
Figura 12. Árvore de backtracking
Fonte: Adaptado de Kreher e Stinson (1999).
3.2 ALGORITMO PARALELO
O algoritmo paralelo para o problema do Clique Máximo foi codificado utilizando
abordagens e estratégias de programação paralela, desenvolvida e estudadas para outros
problemas e com outras tecnologias, assim tendo como objetivo explorar as estratégias e o
desenvolvimento utilizando da tecnologia livre Open MPI. A arquitetura em múltiplos
computadores é ilustrada na Figura 13, onde os computadores serão conectados por meio de
uma rede, estes com memoria e processos locais.
41
Figura 13. Arquitetura em múltiplos computadores
Fonte: Adaptado de Pardalos, Rappe e Resende (2013)
O algoritmo paralelo foi abordado visando uma única maquina com múltiplas threads
e múltiplas maquinas com múltiplas threads, assim faz necessário ajustes específicos para
tratar a escalabilidade que é proporcionada nas duas arquiteturas.
Os autores desenvolveram nos seus trabalhos formas para abordar os problemas e
obter um melhor resultado. O trabalho similar 1 abordou os problemas de duas maneiras, a de
paralelizar operações e subgrafos e o trabalho similar 2 abordou o problema utilizando da
estratégia Mestre-Escravo.
O trabalho similar 1 primeiramente abordou os problemas paralisando operações, de
forma que operações importantes como por exemplo a cópia de um vetor foi paralisada,
resultando em executar todo o processo em uma única unidade de tempo, a segunda
abordagem é a utilização de subgrafos onde é feito a divisão de grafos e processa-los em
paralelo, a Figura 14 ilustra um grafo e seus subgrafos.
42
Figura 14. Divisão do grafo em subgrafos
Fonte: CARDOSO (2012).
O trabalho similar 2 abordou o problema através da estratégia de Mestre-Escravo,
onde o programa mestre é responsável por dividir o grafo em subgrafos e enviar ao programa
escravo, este processa o grafo expandindo-o e ao final retorna uma resposta ao programa
mestre.
Na Figura 15 é ilustrada uma arvore de backtracking paralela, tendo todos os
elementos do conjunto V processados.
43
Figura 15. Árvore de backtracking paralela
Os conjuntos de dados utilizados no algoritmo paralelo são os mesmos utilizados na
programação sequencial, assim foi adicionado variáveis de controle (tais como vértice
recebido, conjunto para saber quais vértices estão processando, entre outras variáveis) para ter
um maior controle da comunicação entre os processos, podendo ser conferido o bloco Main e
as funções no Apêndice B.
3.3 TESTE E RESULTADOS
Nesta seção será descrito o processo de testes e obtenção dos dados utilizando de três
ambientes de execução e contemplando todas as etapas estas que podem ser dividas em três
etapas: (i) única máquina com algoritmo sequencial; (ii) única máquina utilizando o Open
MPI com múltiplas threads; (iii) múltiplas maquinas com múltiplas threads.
Para uma melhor organização e visualização dos resultados obtidos esta seção foi
dividida em três subseções, tais como: Ambientes de Teste e Resultados.
3.3.1 Ambiente de Testes
Os ambientes utilizados para efetuar os testes e obter os dados que são apresentados na
seção seguinte foram divididos em três, que são os seguintes:
Ambiente 1: Notebook com CPU Core 2 Duo P8600 @ 2.40GHZ, com 4GB de
memória RAM DDR2, com o sistema operacional Windows 7 Ultimate e contendo a
biblioteca Open MPI 1.6.1 e Open MPI 1.7 para CygWin.
44
Ambiente 2: Desktop com CPU Core 2 Duo E8400 @ 3.00Ghz, com 4GB de memoria
RAM DDR2, com o sistema operacional Ubuntu 13.10 e contendo a biblioteca Open MPI 1.7.
Ambiente 3: Desktop com CPU Core 2 Duo E8400 @ 3.00Ghz, com 4GB de memoria
RAM DDR2, com o sistema operacional Ubuntu 13.10 em um PenDrive e contendo a
biblioteca Open MPI 1.7.
Desta maneira no ambiente 1 foi utilizado o compilador para a linguagem C++ do
Microsoft Visual Studio 2012 para a biblioteca Open MPI 1.6.1 e para a biblioteca Open MPI
1.7 utilizada no CygWin foi utilizado o GCC versão 4.8.2.
Nos ambientes 2 e 3 foi utilizado a biblioteca Open MPI 1.7 obtida no site oficial, e
habilitado a opção “—enable-heterogeneous” para possibilitar que ambientes com sistema
operacional de 32bits e 64bits possam se comunicar, o compilador para a linguagem C++ foi
utilizado o GCC versão 4.8.2.
As etapas foram dividas em três: (i) Obtenção dos resultados da execução sequencial
dos ambientes 1 e 2, onde foi executado uma única thread do processo em cada ambiente até
encontrar a solução; (ii) Obtenção dos resultados da execução utilizando cinco threads nos
ambientes 1 e 2, onde foi executado cinco threads do processo trabalhando em conjunto em
cada ambiente, de forma os ambientes trabalharam isoladamente; (iii) Obtenção dos
resultados da execução paralela com threads entre os ambientes, de maneira que o primeiro
ambiente contava com cinco threads, sendo uma controladora e as restantes para o
processamento, e os demais ambientes com quatro threads para o processamento, desta forma
as threads destinadas ao processamento recebem da thread controladora os vértices que são
expandidos buscando o grafo, ao final do processamento deste vértice é enviado a solução
encontrada para o controlador e aguardado um novo vértice ou o sinal para encerrar.
Para a execução e obtenção dos dados foram selecionados alguns grafos
disponibilizados pela DIMACS (Center for Discrete Mathematics and Theoretical Computer
Science) e de quatro grafos com a mesma quantidade de vértices e densidades diferentes, estes
e suas características estão descritas na Tabela 2 e Tabela 3, respectivamente. A coluna
Densidade expressa a relação vértices e arestas daquele grafo em questão.
45
Tabela 2. Grafos DIMACS utilizados nas execuções para coleta dos dados.
Grafo
johnson8-2-4
hamming6-4
c-fat200-1
p_hat300-1
brock200_2
keller4
Densidade Vértices
0,5555556
28
0,3492063
64
0,0770854
200
0,75
300
0,4962814
200
0,6491228
171
Arestas
210
704
1534
10933
9876
9435
Tam. Clique Máximo
4
4
12
8
12
11
Tabela 3. Grafos com a mesma quantidade de vértices e densidades diferentes.
Grafo
r128_010
r128_020
r128_030
r128_040
Densidade Vértices
0,10
128
0,20
128
0,30
128
0,40
128
Arestas
1658
3341
4907
6545
Tam. Clique Máximo
5
8
11
13
3.3.2 Resultados
Executou-se o algoritmo exato do Clique Máximo de forma sequencial, utilizando
threads e paralelamente com threads, de maneira que possibilitou obter o tempo que a função
principal utilizou para analisar todo o grafo e encontrar a solução. Os dados foram coletados
de uma média de quatro execuções, visando assim valores com uma maior confiabilidade.
No Quadro 4 pode-se visualizar os resultados obtidos na execução sequencial de cada
grafo utilizado, onde os valores estão expressos em milissegundos.
Quadro 4. Resultados da execução sequencial do Clique Máximo.
Grafo
johnson8-2-4
hamming6-4
c-fat200-1
p_hat300-1
brock200_2
keller4
r128_010
r128_020
r128_030
r128_040
Ambiente 1 –
Windows(ms)
2,5000
5,0000
238,0005
9799,5175
116845,5000
1117707,5000
32,5019
714,5410
17922,5250
1125202,5000
Ambiente 1 –
CygWin(ms)
Ambiente 2(ms)
2,5000
0,6274
5,0000
4,9877
243,5008
195,0968
9972,0400
9080,6000
118637,5000
106505,5000
1129250,0000
1004475,0000
34,2520
26,1291
734,0420
568,3538
17992,2750
14171,3000
1183755,0000
1032782,5000
No Quadro 5 pode-se visualizar os resultados obtidos na execução com múltiplas
threads nos ambientes 1 e 2, onde é executado contendo cinco threads para cada grafo, de
46
maneira que a primeira threads é a controladora, esta que é responsável por dividir o grafo
para que as demais threads processem, os valores estão expressos em milissegundos.
Quadro 5. Resultados da execução do Clique Máximo com múltiplas threads.
Grafo
johnson8-2-4
hamming6-4
c-fat200-1
p_hat300-1
brock200_2
keller4
r128_010
r128_020
r128_030
r128_040
Ambiente 1 –
Windows(ms)
2,5000
10,0000
155,0073
5424,5600
61794,0000
583312,5000
42,0024
433,2748
9612,5375
600171,7500
Ambiente 1 –
CygWin(ms)
Ambiente 2(ms)
3,2500
1,3270
11,5008
2,9346
202,5108
122,3880
6589,1250
5115,9200
64223,2000
60231,4250
596760,0000
578376,2500
43,5025
19,6062
568,0328
378,4318
9870,5700
8846,7800
591519,0000
576717,0000
No Quadro 6 pode-se visualizar um comparativo entre os resultados obtidos a partir
das execuções, onde a segunda coluna está a média dos resultados obtidos na execução
sequencial, a terceira coluna está a média dos resultados obtidos na execução com threads, a
quarta coluna está a média dos resultados obtidos na execução paralela com threads, e a
quinta e ultima coluna é apresentado valores quanto a melhora obtida quanto a utilização da
programação paralela. Na execução em paralelo com threads os ambientes estão executando
em conjunto para achar o Clique Máximo, de maneira que o primeiro ambiente possui cinco
threads, uma a mais que os outros ambientes, visando à necessidade de uma thread que efetue
a divisão do grafo e receba as informações das outras threads. Os valores estão expressos em
milissegundos.
Quadro 6. Comparativo entre as execuções do Clique Máximo.
Grafo
johnson8-2-4
hamming6-4
c-fat200-1
p_hat300-1
brock200_2
keller4
r128_010
r128_020
r128_030
r128_040
Sequencial(ms)
1,8758
4,9959
225,5327
9617,3858
113996,1667
1083810,8333
30,9610
672,3123
16695,3667
1113913,3333
Thread(ms)
2,3590
8,1451
159,9687
5709,8683
62082,8750
586149,5833
35,0370
459,9131
9443,2958
589469,2500
Paralela(ms) Melhora Seq. X Par.
776,5448
Nenhuma
900,0525
Nenhuma
2274,6275
Nenhuma
4064,9825
2,3659 vezes
19916,6250
5,7237 vezes
336983,7500
3,2162 vezes
1483,0850
Nenhuma
1377,3300
Nenhuma
3840,9725
4,3467 vezes
227831,2500
4,8892 vezes
47
Com os resultados obtidos é possível observar que a execução em sequencial
apresentou tempos de execuções menores quando utilizado em grafos pequenos, estes com
quantidades menores de vértices e arestas. A execução com múltiplas threads e em múltiplos
ambientes com threads apresentou melhoras quando os grafos possuem quantidades
expressivas de vértices e arestas, sendo assim os grafos maiores. Pode-se observar que os
grafos menores dispendem mais tempo efetuando a comunicação com as múltiplas threads do
que em tempo de processamento, e os grafos maiores dispendem uma quantidade expressiva
em tempo de processamento do que efetuando a comunicação com as múltiplas threads. Os
resultados para os grafos menos densos podem ser observados através da Figura 16.
2,5000
2,2746
2,0000
SEGUNGOS
1,5000
1,0000
0,7765
0,9001
0,5000
0,0024
0,0019
0,0081
0,0050
0,2255
0,1600
0,0000
johnson8-2-4
Sequencial
hamming6-4
Thread
Paralela
c-fat200-1
Figura 16. Resultados obtidos nos grafos menos densos.
Na Figura 17 é possível observar que há melhora nos grafos P_HAT300-1,
Brock200_2 e KELLER4. Estes grafos possuem quantidades expressivas de vértices e arestas,
assim dispendem mais tempo em processamento e através da utilização de processamento
paralelo obteve-se uma redução expressiva no tempo de processamento dos grafos.
48
1200,0000
1083,8108
1000,0000
SEGUNGOS
800,0000
586,1496
600,0000
400,0000
200,0000
336,9838
9,6174
5,7099
4,0650
113,9962
62,0829
19,9166
p_hat300-1
Sequencial
brock200_2
Thread
Paralela
0,0000
keller4
Figura 17. Resultados obtidos nos grafos mais densos.
Na Figura 18 é possível observar que há melhora nos resultados obtidos através
utilização de processamento paralelo quando aplicada a grafos mais densos, notando-se uma
redução expressiva no tempo de processamento dos grafos.
1113,9133
1200,0000
SEGUNGOS
1000,0000
800,0000
589,4693
600,0000
400,0000
200,0000
0,0310
0,0350
1,4831
0,6723
0,4599
1,3773
16,6954
9,4433
3,8410
r128_020
Thread
r128_030
Paralela
227,8313
0,0000
r128_010
Sequencial
r128_040
Figura 18. Resultados obtidos nos grafos dos grafos com densidades diferentes.
49
4 CONCLUSÕES
Os problemas NP-Completo estão relacionados às diversas áreas de otimização
computacional, devido a isto é constante a busca por métodos, técnicas e estratégias que
tornem estes problemas solúveis em tempo razoável. Desta busca resultou a programação
paralela, onde diversos processos trabalham por um único proposito, obter maior poder
computacional através da divisão do problema em problemas menores. Utilizando da
tecnologia livre Open MPI visa-se abordar estratégias para dividir os problemas NP-Completo
clique máximo e coloração de vértices em problemas menores que possam ser enviados a
outros processos e assim obter uma solução em tempo razoável.
A partir do levantamento realizado foi possível identificar importantes conceitos
envolvendo Problemas NP-Completo, Programação Paralela, Tecnologia Livre Open MPI e o
problemas do Clique Máximo. A sequencia das atividades propostas,
iniciou-se
preferencialmente pela codificação do algoritmo para o problema do Clique Máximo, onde foi
disponibilizada pelo professor orientador a codificação em linguagem python para assim ser
codificada em linguagem C++.
Na sequencia das atividades propostas, a codificação do problema para ser executado
paralelamente foi desenvolvida com base nas estratégias para execução sequencial e paralela
apresentada por Pardalos et al. (1997), esta que mostrou-se bastante eficiente na resolução de
grafos densos utilizando a tecnologia livre Open MPI, onde foi levado em conta as
particularidades e limitações da biblioteca nas versões abordadas.
Para coleta dos dados que posteriormente foram analisados comparativamente,
caracterizando o penúltimo objetivo foram executados quatro testes em cada uma das três
etapas, sequencial, paralela com threads e múltiplos computados paralelamente com threads,
assim calculada a média das execuções e efetuada a comparação.
Para se reduzir o tempo de execução em relação às tecnologias sequencias pode-se
utilizar a tecnologia livre Open MPI visando dividir a carga de processamento utilizando
múltiplos computadores com múltiplas threads, onde cada vértice tem a responsabilidade de
encontrar o clique Máximo contendo o seu vértice de responsabilidade.
A programação paralela utilizando a tecnologia livre Open MPI proporcionou em
relação a
programação sequencial soluções 2.36, 3.21 e até 5 vezes mais rápido em
50
determinados grafos. Observando os resultados obtidos acredita-se que para grafos maiores o
paralelismo seja justificável, assim como para grafos com maiores densidades.
Na busca pela melhor maneira de abordar as estratégias estudadas, algumas
dificuldades foram enfrentadas, tais como a falta de uma ampla depuração por parte da
biblioteca do Open MPI na versão para Sistema Operacional Windows, o consumo excessivo
de memória em alguns grafos devido a conversão deficiente do algoritmo em linguagem
Python para linguagem C++, a dificuldade em encontrar documentação para solucionar
problemas de compatibilidade de tipos para o envio dos dados entre os processos, a falta de
suporte a conexão remota segura sem senha por parte do Sistema Operacional Windows, a
necessidade de mudar e preparar um novo ambiente de execução devido a incompatibilidade
em uma conexão remota segura, a impossibilidade em utilizar os computadores da UNIVALI
para efetuar as execuções e obter os dados devido a não possuírem leitores de CD/DVD que
possibilitariam a utilização de um sistema operacional com Linux. Devido a estas dificuldades
encontradas não foi possível concluir a abordagem ao problema da Coloração de Vértices
proposto nos objetivos deste trabalho, sendo assim foi mantido a fundamentação teórica do
mesmo para futuros trabalhos.
Como trabalhos futuros, podem-se citar: (i) Utilizar a tecnologia livre Open MPI
destinada ao problema da Coloração de Vértices e a outros problemas, visando assim utilizar a
estratégia ou desenvolver com base na desenvolvida neste trabalho; (ii) Utilizar a tecnologia
livre Open MPI juntamente com a tecnologia CUDA; (iii) Incluir técnicas de programação
dinâmica juntamente com a tecnologia livre Open MPI; (iv) Utilizar a tecnologia livre Open
MPI para o problema abordado neste trabalho e a outros problemas, procurando incluir
formas de melhorar a comunicação entre os processos através da criação de tipos compostos.
51
REFERÊNCIAS
AGUIAR, F. N.; HONORATO, G. S. C. Metaheurística Busca Tabu para o Problema de
Coloração de Grafos. In: Anais XXXVII Simpósio Brasileiro de Pesquisa Operacional,
XXXVII, 2005, Gramado, p. 2497-2504.
AGUIAR, M. S. Análise Formal da Complexidade de Algoritmos Genéticos. 1998. 75f.
Dissertação (Mestrado em Ciência da Computação) - Instituto de Informática, Universidade
Federal do Rio Grande do Sul, Porto Alegre, 1998.
ALECRIM, E. O que é Linux. Disponível: <http://www.oficinadanet.com.br/artigo/1192/>.
Acesso em: 05 Nov. de 2013.
ARORA, S.; BARAK, B. Computational Complexity: a modern approach. 1. ed., [S.l.]:
Cambridge University Press, 2009. ISBN 9780521424264
BARBOSA, I. G.; MIRANDA, D. C.; ILÍDIO, R. Uma Heurística Baseada em Grasp para o
Problema do Clique Máximo. Disponível:
<http://homepages.dcc.ufmg.br/~nivio/cursos/pa06/seminarios/seminario8/seminario8.pdf>.
Acesso em: 15 Mai. 2013.
CAMPOS, A. O que é Linux. Disponível: <http://br-linux.org/2008/01/faq-linux.html>.
Acesso em: 05 Nov. de 2013.
CARDOSO, E. A. Análise Comparativa de Algoritmos NP-Completo executados em CPU e
GPU utilizando CUDA. 2012. 84 f. Graduação (Bacharelado em Ciência da Computação) –
Universidade do Vale do Itajaí, Itajaí, 2012.
CARMO R.; ZÜGE, A. Branch and bound algorithms for the maximum clique problem under
a unified framework. In: J Braz Compit Soc, 18, 2012. p 137-151.
CAVIQUE, L.; REGO, C.; THEMIDO, I. Estruturas de vizinhança e procura local no
problema da clique máxima. Disponível:
<http://lcavique.no.sapo.pt/publicacoes/Clique%20Tabu.pdf>. Acesso em: 15 Mai. 2013.
COOK S. A. The Complexity of Theorem-Proving Procedures. In: University of Toronto,
1971. p 151-158.
CYGWIN. CYGWIN. Disponível: < http://www.cygwin.com/>. Acesso em: 03 Nov. de
2013.
DIMACS. DIMACS Implementation Challenges. Disponível em:
<http://dimacs.rutgers.edu/Challenges/>. Acesso em: 06 Set. 2013.
GAREY, M. R.; JOHNSON, D. S. Computers and Intractability: a guide to the theory of NPCompleteness. [S.l.]: Bell Telephone Laboratories Inc, 1979. ISBN 0-7167-1044-7
GONÇALVES, G. M. CYGWIN. Disponível: <
http://paginas.fe.up.pt/~gil/ensino/prg/cygwin.html >. Acesso em: 03 Nov. de 2013.
52
GRAHAM, R. L.; WOODALL, T. S.; SQUYRES, J. M. Open MPI: A Flexible High
Performance MPI. 2005. Disponível: <http://www.open-mpi.org/papers/ppam-2005/>. Acesso
em: 02 abr. 2013.
KREHER, D. L.; STINSON, D. R. Combinatorial Algorithms: Generation, Enumeration, and
Search. Rockville: CRC Press, 1999.
LOPES, L. S. Uma Heurística baseada em algoritmos genéticos aplicada ao problema de
cobertura de conjuntos. 1995. 77 f. Dissertação (Mestrado em Computação Aplicada) Instituto Nacional de Pesquisas Espaciais. São José dos Campos, Março de 1995.
NEVES, M. V. Modelagem e Dimensionamento do Custo de Migração de Processos em
Programas MPI. 2009. 75 f. Dissertação (Mestrado em Ciência da Computação) - Instituto de
Informática, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2009.
NIKOLAY, L. On the Complexity of Maximum Clique Algorithms: usage of coloring
heuristics leads to the Ω(20.2n) algorithm running time lower bound. Disponível:
<http://arxiv.org/ftp/arxiv/papers/1303/1303.2546.pdf>. Acesso em: 01 Mar. 2013.
OPEN MPI. The OpenMPI Project, 2013. Disponível em: <http://www.open-mpi.org/faq/>.
Acesso em: 09 mar. 2013.
PAPADIMITRIOU, C. H.; STEIGLITZ, K. Combinatorial Optimization: algorithms and
complexity. Englewood Cliffs, NJ: Prentice Hall, 1998.
PARDALOS, P. M.; RAPPE, J.; RESENDE, M. G. C. An Exact Parallel Algorithm For The
Maximum Clique Problem. Disponível em:
<http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.51.8498>. Acesso em: 15 Mai.
2013.
PEREIRA, G. W. Aplicação da Técnica de Recozimento Simulado em Problemas de
Planejamento Florestal Multiobjetivo. 2004. 84 f. Dissertação (Mestrado em Ciência da
Computação) - Instituto de Ciências Exatas, Universidade Federal de Minas Gerais. Belo
Horizonte, Março de 2004.
Python. Python Programming Language, 2013. Disponível em: <http://www.python.org/>.
Acesso em: 15 Out. 2013.
SIPSER, M. Introdução à Teoria da Computação. 2. ed., São Paulo: Cengage Learning, 2007.
ISBN: 978-85-221-0499-4
STALLINGS, W. Arquitetura e organização de computadores. Ed. São Paulo: Pearson Pratice
Hall, 2010.
TANEMBAUM, A. S.; STEEN M. V. Sistemas Distribuídos: princípios e paradigmas, 2. ed.
São Paulo: Pearson Prentice Hall, 2007.
TANEMBAUM, A. S. Sistemas operacionais modernos. São Paulo: Pearson Prentice Hall,
2003.
TOSCANI, L. V.; VELOSO, P. A. S. Complexidade de algoritmos. Porto Alegre, RS:
Bookman, 2005.
53
ZIVIANI , N. Projeto de algoritmos com implementações em PASCAL e C. 2 ed. São Paulo:
Cengage Learning , 2011.
54
GLOSSÁRIO
Decidível
Satisfazibilidade
Caixeiro Viajante
Cygwin
DIMACS
Linux
Python
É um problema que a resposta atribuída pode ser “sim” ou “não”, é a
tradução do termo decibility, encontrado nas referências.
É considerado o primeiro problema NP-Completo, este tem por
finalidade comprovar se uma expressão com diversas variáveis booleanas
é satisfazível, é a tradução do termo satisfiability encontrado nas
referências.
Consiste em encontrar o caminho de menor distância para percorrer um
conjunto de cidades, de maneira que visite todas as demais uma única vez
e ao final regresse a cidade inicial.
É um software que permite emular o ambiente Linux no sistema
operacional Windows, assim possibilitando utilizar diversas ferramentas
para Linux.
É uma colaboração entre as universidades Rutgers University e Princeton
University e diversas empresas buscando desenvolver estudos na área de
matemática discreta e da teoria da computação.
É um núcleo de código-fonte aberto e o ao mesmo tempo sistema
operacional, desenvolvido por Linus Torvalds e mantido por diversas
comunidades, como privadas e acadêmicas.
É uma linguagem de programação interpretada, orientada a objetos.
Gerenciada pela organização sem fins lucrativos Python Software
Foundation.
55
APÊNDICE A. ALGORITMO SEQUENCIAL
A.1 CLIQUE MÁXIMO
Quadro 7. Clique Máximo – Função MaxClique
Void maxClique(int l){
counter++;
if ( l == 0 ){
optSize = 0;
inicializa_vetor(optClique, grafo.numero_vertices);
counter = 0;
}
if ( l > optSize ){
optSize = l;
for (int i=0; i < optClique.numero_elementos; i++) {
optClique.elementos[i] = 0;
}
optClique.numero_elementos = 0;
for (int i=0; i < X.numero_elementos; i++) {
if ( X.elementos[i] != -1 ){
optClique.elementos[optClique.numero_elementos] = X.elementos[i];
optClique.numero_elementos++;
}
}
}
if ( l == 0 ){
C.elementos[l] = V;
}else{ // Faz Intersecção
for (int i=0; i < C.elementos[l].numero_elementos; i++) {
C.elementos[l].elementos[i] = 0;
}
C.elementos[l].numero_elementos = 0;
int posX = X.elementos[l-1];
for (int i=0; i < A.elementos[posX].numero_elementos; i++){
for (int j=0; j < B.elementos[posX].numero_elementos; j++){
if ( A.elementos[posX].elementos[i] == B.elementos[posX].elementos[j]){
for (int ij=0; ij < C.elementos[l-1].numero_elementos; ij++){
if (A.elementos[posX].elementos[i] == C.elementos[l-1].elementos[ij]){
C.elementos[l].elementos[C.elementos[l].numero_elementos] =
A.elementos[posX].elementos[i];
C.elementos[l].numero_elementos++;
break;
}
}
break;
}
56
}
}
}
for (int i=0; i < C.elementos[l].numero_elementos; i++){
X.elementos[l] = C.elementos[l].elementos[i];
maxClique(l + 1);
}
limpaVetor (X, l);
}
57
APÊNDICE B. ALGORITMO PARALELO
B.1 BLOCO MAIN
Quadro 8. Clique Máximo – Bloco Main
int main ( int argc, char** argv ){
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &processoAtual);
MPI_Comm_size(MPI_COMM_WORLD, &totalProcessos);
ofstream arquivo;
string nome_arquivo = argv[argc - 1];
if (totalProcessos < 2 || !inicializa_dimacs(grafo, nome_arquivo)){
MPI_Finalize();
return 0;
}
inicializa_vetor(V, grafo.numero_vertices);
inicializa_vetor2(A, grafo.numero_vertices );
inicializa_vetor2(B, grafo.numero_vertices);
inicializa_vetor2(C, grafo.numero_vertices);
inicializa_vetorArestas(A, grafo);
inicializa_vetorMaiores(B, grafo.numero_vertices);
inicializa_vetorCliques(C, grafo.numero_vertices);
inicializa_vetorVertices(V, grafo.numero_vertices);
inicializa_vetorX(X, grafo.numero_vertices);
// Inicializa Vetor A
// Inicializa Vetor B
// Inicializa Vetor V
// Inicializa Vetor V
// Inicializa Vetor X
optSize = 0;
inicializa_vetor(optClique, grafo.numero_vertices);
counter = 0;
C.elementos[0] = V;
inicio = chrono::system_clock::now();
if (processoAtual == PROCESSO_MASTER){ // Master
optCliqueRecebido = new VetorInt[grafo.numero_vertices];
optSizeRecebido = new int[grafo.numero_vertices];
verticeProcessado = new int[grafo.numero_vertices];
for (int i=0; i < grafo.numero_vertices; i++){
verticeProcessado[i] = -1;
}
processoLivre = new int[totalProcessos-1];
for (int i=0; i < totalProcessos-1; i++){
processoLivre[i] = 1;
}
58
maxCliqueMaster(0);
int iProbeFlag;
while(!fimProcessamento){
fimProcessamento = true;
for (int i=0; i < totalProcessos-1; i++){
if (processoLivre[i] == 0){
fimProcessamento = false;
break;
}
}
if (!fimProcessamento){
MPI_Iprobe(MPI_ANY_SOURCE,MPI_ANY_TAG,
MPI_COMM_WORLD,&iProbeFlag,&iProbeStatus);
if (iProbeFlag){
int iProbeSource = iProbeStatus.MPI_SOURCE;
int verticeRecebido;
MPI_Recv(&verticeRecebido,1,MPI_INT,iProbeSource,MPI_ANY_TAG,
MPI_COMM_WORLD,&status);
optCliqueRecebido[verticeRecebido].elementos = new int[grafo.numero_vertices];
MPI_Recv(&optCliqueRecebido[verticeRecebido].numero_elementos,1,MPI_INT,
iProbeSource,MPI_ANY_TAG,MPI_COMM_WORLD,&status);
MPI_Recv(optCliqueRecebido[verticeRecebido].elementos,grafo.numero_vertices,
MPI_INT,iProbeSource,MPI_ANY_TAG,MPI_COMM_WORLD,&status);
MPI_Recv(&optSizeRecebido[verticeRecebido],1,MPI_INT,iProbeSource,
MPI_ANY_TAG,MPI_COMM_WORLD,&status);
verticeProcessado[verticeRecebido] = 1;
processoLivre[iProbeSource-1] = 1;
}
}
}
for (int i=0; i < totalProcessos-1; i++){
MPI_Send(&i, 1, MPI_INT, i+1, 9, MPI_COMM_WORLD);
}
tempoS = chrono::system_clock::now() - inicio;
tempoMs = chrono::system_clock::now() - inicio;
string strCounter = "\nCounter: " + to_string2(counter);
string strTempoS = "\nTempo em segundos: " + to_string2(tempoS.count()) + " s";
string strTempoMs = "\nTempo em milisegundos: " + to_string2(tempoMs.count()) + " ms";
printf("%s", strCounter.c_str());
printf("%s", strTempoS.c_str());
printf("%s", strTempoMs.c_str());
// Coloca todos os cliques gerados em uma string para poder escrever no arquivo
string strOptCliqueRecebido = "";
for (int i=0; i < grafo.numero_vertices; i++){
59
strOptCliqueRecebido += "\noptSize: " + optSizeRecebido[i];
strOptCliqueRecebido += printOptClique(optCliqueRecebido[i]);
strOptCliqueRecebido += "\n";
if ( optSizeRecebido[posMaiorClique] < optSizeRecebido[i] ){
posMaiorClique = i;
}
}
string strOptSize = "\nMaior - optSize: " + to_string2(optSizeRecebido[posMaiorClique]);
string strOptClique = "\nMaior - optClique: " +
printOptClique(optCliqueRecebido[posMaiorClique]);
printf("%s", strOptSize.c_str());
printf("%s", strOptClique.c_str());
int arquivoTime = time(NULL);
arquivo.open ("./Solucao/"+grafo.nome_grafo+"_"+to_string2(arquivoTime)+".txt");
arquivo << strOptSize;
arquivo << strOptClique;
arquivo << strCounter;
arquivo << strTempoS;
arquivo << strTempoMs;
arquivo << strOptCliqueRecebido;
arquivo.close();
}else{ // Slave
bool whileInfinito = true;
while(whileInfinito){
int iProbeFlag;
MPI_Iprobe(MPI_ANY_SOURCE,MPI_ANY_TAG,
MPI_COMM_WORLD,&iProbeFlag,&iProbeStatus);
if (iProbeFlag){
int iProbeTag = iProbeStatus.MPI_TAG;
if (iProbeTag == 9){
whileInfinito = false;
MPI_Finalize();
return 0;
}else{
MPI_Recv(&X.numero_elementos,1,MPI_INT,PROCESSO_MASTER,
MPI_ANY_TAG,MPI_COMM_WORLD,&status);
MPI_Recv(X.elementos,grafo.numero_vertices,MPI_INT,
PROCESSO_MASTER,MPI_ANY_TAG,MPI_COMM_WORLD,&status);
verticeRecebido = X.elementos[0];
maxCliqueSlave(1);
MPI_Send(&verticeRecebido, 1, MPI_INT,
PROCESSO_MASTER, 1, MPI_COMM_WORLD);
MPI_Send(&optClique.numero_elementos, 1,
MPI_INT, PROCESSO_MASTER, 1, MPI_COMM_WORLD);
MPI_Send(optClique.elementos, grafo.numero_vertices,
MPI_INT, PROCESSO_MASTER, 1, MPI_COMM_WORLD);
MPI_Send(&optSize, 1, MPI_INT, PROCESSO_MASTER, 1, MPI_COMM_WORLD);
60
delete[] X.elementos;
inicializa_vetorX(X, grafo.numero_vertices);
}
}
}
}
MPI_Finalize();
return 0;
}
B.2 CLIQUE MÁXIMO MASTER
Quadro 9. Clique Máximo – Função MaxCliqueMaster
void maxCliqueMaster(int l){
for (int i=0; i < C.elementos[l].numero_elementos; i++){
int iProbeFlag;
bool enviado = false;
X.elementos[l] = C.elementos[l].elementos[i];
while(!enviado){
for (int j=0; j < totalProcessos-1; j++){
if ( processoLivre[j] == 1){
MPI_Send(&X.numero_elementos, 1, MPI_INT, j+1, 1, MPI_COMM_WORLD);
MPI_Send(X.elementos, grafo.numero_vertices, MPI_INT, j+1, 1,
MPI_COMM_WORLD);
processoLivre[j] = 0;
enviado = true;
break;
}
}
MPI_Iprobe(MPI_ANY_SOURCE,MPI_ANY_TAG,
MPI_COMM_WORLD,&iProbeFlag,&iProbeStatus);
if (iProbeFlag){
int iProbeSource = iProbeStatus.MPI_SOURCE;
int verticeRecebido;
MPI_Recv(&verticeRecebido,1,MPI_INT,iProbeSource,
MPI_ANY_TAG,MPI_COMM_WORLD,&status);
optCliqueRecebido[verticeRecebido].elementos = new int[grafo.numero_vertices];
MPI_Recv(&optCliqueRecebido[verticeRecebido].numero_elementos,1,
MPI_INT,iProbeSource,MPI_ANY_TAG,MPI_COMM_WORLD,&status);
MPI_Recv(optCliqueRecebido[verticeRecebido].elementos,grafo.numero_vertices,
MPI_INT,iProbeSource,MPI_ANY_TAG,MPI_COMM_WORLD,&status);
MPI_Recv(&optSizeRecebido[verticeRecebido],1,MPI_INT,iProbeSource,MPI_ANY_TAG
,MPI_COMM_WORLD,&status);
verticeProcessado[verticeRecebido] = 1;
processoLivre[iProbeSource-1] = 1;
}
}
}
}
61
B.3 CLIQUE MÁXIMO SLAVE
Quadro 10. Clique Máximo – Função MaxCliqueSlave
void maxCliqueSlave(int l){
counter++;
if ( l == 0 ){
optSize = 0;
inicializa_vetor(optClique, grafo.numero_vertices);
counter = 0;
}
if ( l > optSize ){
optSize = l;
for (int i=0; i < optClique.numero_elementos; i++) {
optClique.elementos[i] = 0;
}
optClique.numero_elementos = 0;
for (int i=0; i < X.numero_elementos; i++) {
if ( X.elementos[i] != -1 ){
optClique.elementos[optClique.numero_elementos] = X.elementos[i];
optClique.numero_elementos++;
}
}
}
if ( l == 0 ){
C.elementos[l] = V;
}else{ // Faz Intersecção
for (int i=0; i < C.elementos[l].numero_elementos; i++) {
C.elementos[l].elementos[i] = 0;
}
C.elementos[l].numero_elementos = 0;
int posX = X.elementos[l-1];
for (int i=0; i < A.elementos[posX].numero_elementos; i++){
for (int j=0; j < B.elementos[posX].numero_elementos; j++){
if ( A.elementos[posX].elementos[i] == B.elementos[posX].elementos[j]){
for (int ij=0; ij < C.elementos[l-1].numero_elementos; ij++){
if (A.elementos[posX].elementos[i] == C.elementos[l-1].elementos[ij]){
C.elementos[l].elementos[C.elementos[l].numero_elementos] =
A.elementos[posX].elementos[i];
C.elementos[l].numero_elementos++;
break;
}
}
break;
62
}
}
}
}
for (int i=0; i < C.elementos[l].numero_elementos; i++){
X.elementos[l] = C.elementos[l].elementos[i];
maxCliqueSlave(l + 1);
}
limpaVetor (X, l);
}