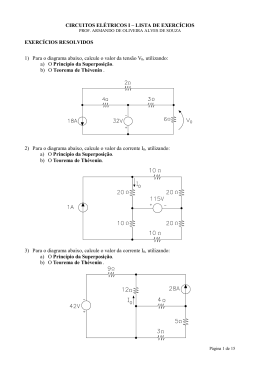
CIRCUITOS ELÉTRICOS I – LISTA DE EXERCÍCIOS
EXERCÍCIOS RESOLVIDOS
1) Para o diagrama abaixo, calcule o valor da tensão V0, utilizando:
a) O Princípio da Superposição.
b) O Teorema de Thévenin .
2) Para o diagrama abaixo, calcule o valor da corrente I0, utilizando:
a) O Princípio da Superposição.
b) O Teorema de Thévenin.
3) Para o diagrama abaixo, calcule o valor da corrente I0, utilizando:
a) O Princípio da Superposição.
b) O Teorema de Thévenin .
Página 1 de 15
4) Para o diagrama abaixo, calcule o valor da tensão V0, utilizando:
a) O Princípio da Superposição.
b) O Teorema de Thévenin .
5) Determine no circuito abaixo, utilizando Análise de Malhas, o valor da tensão V0.
6) Determine no circuito abaixo, utilizando Análise de Malhas, o valor da tensão V0.
Página 2 de 15
7) Determine no circuito abaixo, utilizando Análise de Malhas, o valor da tensão V0.
8) Determine no circuito abaixo, utilizando Análise de Malhas, o valor da tensão V0.
9) Determine no circuito abaixo, utilizando Análise de Nodal, o valor da corrente I0.
Página 3 de 15
10) Determine no circuito abaixo, utilizando Análise de Nodal, o valor da corrente I0.
11) Determine no circuito abaixo, utilizando Análise de Nodal, o valor da corrente I0.
12) Determine no circuito abaixo, utilizando Análise de Nodal, o valor da corrente I0.
Página 4 de 15
Resolução
1)
a)
Fonte de 32 V
Fonte de 18 A
R EQ _ bc = 2 Ω (6 // 3)
R EQ _ ab = 2 Ω (( 4 + 2) // 3)
V0 ' = −
6Ω
⋅ 32V = −24V
6Ω + 2Ω
4Ω
⋅ 18A = 9 A
4Ω + 4Ω
V0 " = −2 ⋅ I A = −18V
IA =
V0 = V0 '+ V0 " = ( −24) + ( −18) = −42V
b)
IB =
VTH
4Ω
⋅ 18A = 8A
4Ω + 5Ω
= −32 − 3.I B = −56V
R TH = 2 Ω ((4 + 2) // 3)
V0 = −
6Ω
⋅ 56V = − 42V
6Ω + 2Ω
2)
a)
Fonte de 115 V
I0 ' = −
Fonte de 1 A
115V
= −2,3A
20Ω + 10Ω + 20Ω
I0" =
30Ω
⋅ 1A = 0,6 A
30Ω + 20Ω
I 0 = I 0 '+ I 0 " = (− 2,3) + (0,6) = −1,7 A
Página 5 de 15
b)
VTH = − 115 + 20 + 10 = −85V
R TH = 30 Ω (10 + 20)
I0 = −
85V
= − 1,7 A
30Ω + 20Ω
3)
a)
Fonte de 42 V
I0 ' =
Fonte de 28 A
42 V
9Ω
= 2A
I0" = −
⋅ 28A = −12 A
9Ω + 12Ω
9Ω + 12Ω
I 0 = I 0 '+ I 0 " = (2) + (−12) = −10A
b)
VTH = −42 + 252 = 210V
R TH = 9 Ω
I0 = −
210 V
= − 10A
9Ω + 12Ω
Página 6 de 15
4)
a)
Fonte de 64 V
V0 ' = −
b)
Fonte de 8 A
2Ω
.64V = −16V
2 Ω + 2 Ω + 4Ω
V0 = V0 '+ V0 " = ( −16) + (12) = −4 V
VTH = 16 + 32 − 64 = −16V
R TH = 6 Ω ((6 // 3) + 4)
V0 = −
5)
IA = I3
6Ω
⋅ 8A = 6A
2 Ω + 6Ω
V0 " = 2.I A = 12 V
IA =
2Ω
⋅16V = − 4V
2Ω + 6Ω
I 2 = 3A
⎡ 10 − 3 − 5⎤ ⎡ I1 ⎤ ⎡ − 4.I 3 ⎤
⎥
⎢ − 3 6 − 3⎥ ⋅ ⎢ 3 ⎥ = ⎢ V
(1) 10.I1 − 9 − 5.I 3 = − 4.I 3
X
⎥
⎥ ⎢ ⎥ ⎢
⎢
⎢⎣ − 5 − 3 14 ⎥⎦ ⎢⎣ I 3 ⎥⎦ ⎢⎣34 + 4.I3 ⎥⎦
(3) − 5.I1 − 9 + 14.I 3 = 34 + 4.I 3
(1) 10.I1 − I 3 = 9
(3) − 5.I1 + 10.I 3 = 43 ( x 2) (3) − 10.I1 + 20.I 3 = 86
(1) + (3) 19.I 3 = 95 ⇒ I 3 = 5A
V0 = 3.I 3 ⇒ V0 = 15V
Página 7 de 15
6)
IA = I3
I1 = −2 A
⎡ 4 − 1 − 3⎤ ⎡− 2⎤ ⎡ − VX ⎤
⎥
⎢ − 1 4 − 1⎥ ⋅ ⎢ I ⎥ = ⎢
6
(2) 2 + 4.I 2 − I 3 = 6
⎥
⎥ ⎢ 2⎥ ⎢
⎢
⎢⎣ − 3 − 1 8 ⎥⎦ ⎢⎣ I 3 ⎥⎦ ⎢⎣ − 6 + 5.I 3 ⎥⎦
(3) 6 − I 2 + 8.I 3 = −6 + 5.I 3
(2) 4.I 2 − I 3 = 4
(3) − I 2 + 3.I 3 = −12 ( x 4) (3) − 4.I 2 + 12.I 3 = −48
( 2) + (3) 11.I3 = −44 ⇒ I 3 = − 4A
V0 = 2.I 3 ⇒ V0 = −8V
7)
I A = I1 − I 3
I2 = 4A
⎡ 12 − 5 − 3 ⎤ ⎡ I1 ⎤ ⎡ − 164 ⎤
⎢ − 5 8 − 3 ⎥ ⋅ ⎢ 4 ⎥ = ⎢ 64 + V ⎥
(1) 12.I1 − 20 − 3.I 3 = −164
X ⎥
⎥ ⎢ ⎥ ⎢
⎢
⎢⎣ − 3 − 3 13,5⎥⎦ ⎢⎣ I 3 ⎥⎦ ⎢⎣3.I1 − 3.I3 ⎥⎦
(3) − 3.I1 − 12 + 13,5.I 3 = 3.I1 − 3.I 3
(1) 12.I1 − 3.I 3 = −144
(3) − 6.I1 + 16,5.I 3 = 12 ( x 2) (3) − 12.I1 + 33.I 3 = 24
(1) + (3) 30.I3 = −120 ⇒ I3 = −4A
V0 = 3,5.I 3 ⇒ V0 = −14 V
8)
I A = I 2 − I1
I3 = 7 A
15
⎤
⎡ 7 − 2 − 2 ⎤ ⎡ I1 ⎤ ⎡
⎢ − 2 5 − 2⎥ ⋅ ⎢ I ⎥ = ⎢− 8.I + 8.I − 25⎥
(1) 7.I1 − 2.I 2 − 14 = 15
2
1
⎥
⎥ ⎢ 2⎥ ⎢
⎢
⎥⎦
⎢⎣ − 2 − 2 6 ⎥⎦ ⎢⎣ 7 ⎥⎦ ⎢⎣
10 + VX
(2) − 2.I1 + 5.I 2 − 14 = −8.I 2 + 8.I1 − 25
(1) 7.I1 − 2.I 2 = 29 ( x 6,5) (1) 45,5.I1 − 13.I 2 = 188,5
( 2) − 10.I1 + 13.I 2 = −11
(1) + ( 2) 35,5.I1 = 177,5 ⇒ I1 = 5A
V0 = 2.I1 ⇒ V0 = 10 V
9)
V1 = V3 + 1
V2 = −3V
⎡ 8 − 5 0⎤ ⎡ V3 + 1⎤ ⎡ I X − 10 ⎤
⎢ − 5 5 0⎥ ⋅ ⎢ − 3 ⎥ = ⎢ − I − 10⎥
(1) 8.V3 + 8 + 15 = I X − 10
⎥
⎥ ⎢ Y
⎥ ⎢
⎢
⎢⎣ 0
0 1 ⎥⎦ ⎢⎣ V3 ⎥⎦ ⎢⎣ − I X − 21⎥⎦
(3) V3 = − I X − 21
(1) + (3) 9.V3 + 23 = −31 ⇒ V3 = −6V
I 0 = − V3 .1 ⇒ I 0 = 6A
Página 8 de 15
10)
V1 = V3 + 10
V2 = 8V
0
0 ⎤ ⎡ V3 + 10 ⎤ ⎡ − 6 + I X ⎤
⎡1,5
⎢0
0,5 − 0,5⎥ ⋅ ⎢ 8 ⎥ = ⎢ 6 + I Y ⎥⎥
(1) 1,5.V3 + 15 = −6 + I X
⎥ ⎢
⎥ ⎢
⎢
⎢⎣ 0 − 0,5 1,5 ⎥⎦ ⎢⎣ V3 ⎥⎦ ⎢⎣ 11 − I X ⎥⎦
(3) − 4 + 1,5.V3 = 11 − I X
(1) + (3) 3.V3 + 11 = 5 ⇒ V3 = −2 V
I 0 = V3 .1 ⇒ I 0 = −2 A
11)
V2 = V1 + 3
V3 = 10 V
0
− 5 ⎤ ⎡ V1 ⎤ ⎡ 32 − I X ⎤
⎡8
⎢0
3,5 − 0,5⎥ ⋅ ⎢ V1 + 3⎥ = ⎢ I X + 50 ⎥⎥
(1) 8.V1 − 50 = 32 − I X
⎥ ⎢
⎥ ⎢
⎢
⎢⎣ − 5 − 0,5 5,5 ⎥⎦ ⎢⎣ 10 ⎥⎦ ⎢⎣ I Y − 5 ⎥⎦
(2) 3,5.V1 + 10,5 − 5 = I X + 50
(1) + ( 2) 11,5.V1 − 44,5 = 82 ⇒ V1 = 11V
I 0 = V1.3 ⇒ I 0 = 33A
12)
V1 = V2 − 11
V3 = −5V
0
− 1 ⎤ ⎡ V2 − 11⎤ ⎡ − I X − 2 ⎤
⎡1,5
⎢0
1,75 − 0,25⎥ ⋅ ⎢ V2 ⎥ = ⎢ I X + 1,5 ⎥⎥
⎥ ⎢
⎥ ⎢
⎢
⎢⎣ − 1 − 0,25 1,25 ⎥⎦ ⎢⎣ − 5 ⎥⎦ ⎢⎣ 2 − I Y ⎥⎦
(1) 1,5.V2 − 16,5 + 5 = −I X − 2
( 2) 1,75.V2 + 1,25 = I X + 1,5
(1) + (2) 3,25.V2 − 10, 25 = −0,5 ⇒ V2 = 3V
I 0 = − V2 .1,5 ⇒ I 0 = −4,5A
Página 9 de 15
EXERCÍCIOS PROPOSTOS - TP
1) Para o diagrama abaixo, calcule o valor da tensão V0, utilizando:
a) O Princípio da Superposição.
b) O Teorema de Thévenin .
R.: V0 = - 30V
2) Para o diagrama abaixo, calcule o valor da corrente I0, utilizando:
a) O Princípio da Superposição.
b) O Teorema de Thévenin .
R.: I0 = -2A
3) Determine no circuito abaixo, utilizando Análise de Malhas, o valor da tensão V0.
R.: V0 = - 25,5V
Página 10 de 15
4) Determine no circuito abaixo, utilizando Análise de Malhas, o valor da tensão V0.
R.: V0 = -35V
5) Determine no circuito abaixo, utilizando Análise de Nodal, o valor da corrente I0.
R.: I0 = 42A
6) Determine no circuito abaixo, utilizando Análise de Nodal, o valor da corrente I0.
R.: I0 = 21,5A
Página 11 de 15
SIMULADO DE PROVA RESOLVIDO
1) Determine no circuito abaixo, utilizando Análise de Malhas, o valor da tensão V0. (3,0 PTS)
2) Determine no circuito abaixo, utilizando Análise de Nodal, o valor da corrente I0. (3,0 PTS)
3) Para o diagrama abaixo, calcule o valor da tensão V0, utilizando:
a) O Princípio da Superposição. (2,0 PTS)
b) O Teorema de Thévenin . (2,0 PTS)
Página 12 de 15
Resolução:
1)
IA = I3 − I2
I 1 = −4 A
⎡ 3 − 1 − 2⎤ ⎡− 4⎤ ⎡ − 10 − VX ⎤
⎢ − 1 4 − 2⎥ ⋅ ⎢ I ⎥ = ⎢6.I − 6.I ⎥
(2) 4 + 4.I 2 − 2.I 3 = 6.I 3 − 6.I 2
2⎥
⎢
⎥ ⎢ 2⎥ ⎢ 3
⎢⎣ − 2 − 2 6 ⎥⎦ ⎢⎣ I 3 ⎥⎦ ⎢⎣ − 4, 4 ⎥⎦
(3) 8 − 2.I 2 + 6.I 3 = −4, 4
(2) 10.I 2 − 8.I 3 = −4
(3) − 2.I 2 + 6.I 3 = −12,4 ( x 5) (3) − 10.I 2 + 30.I 3 = −62
(2) + (3) 22.I 3 = −66 ⇒ I 3 = −3A
V0 = 1.I 3 ⇒ V0 = −3V
2)
V1 = 2V
V3 = V2 − 3
⎡ 18 − 10 − 8⎤ ⎡ 2 ⎤ ⎡ 6 + I Y ⎤
⎢− 10 16
0 ⎥ ⋅ ⎢ V2 ⎥ = ⎢ 2 + I X ⎥
( 2) − 20 + 16.V2 = 2 + I X
⎢
⎥ ⎢
⎥ ⎢
⎥
⎢⎣ − 8
0
10 ⎥⎦ ⎢⎣V2 − 3⎥⎦ ⎢⎣ − 42 − I X ⎥⎦
(3) − 16 + 10.V2 − 30 = −42 − I X
(2) + (3) 26.V2 − 66 = −40 ⇒ V2 = 1V
I 0 = V2 .6 ⇒ I 0 = 6 A
3)
a)
Fonte de 15 V
V0 ' = −
b)
Fonte de 6 A
1Ω
.15V = − 7,5V
1Ω + 1Ω
1Ω
⋅ 6 A = 3A
1Ω + 1Ω
V0 " = 1.I A = 3V
IA =
V0 = V0 '+ V0 " = ( −7,5) + (3) = −4,5V
VTH = −15 + 6 = −9 V
R TH = 1 Ω
V0 = −
1Ω
⋅ 9 V = − 4,5V
1Ω + 1Ω
Página 13 de 15
SIMULADO DE PROVA PROPOSTO (A)
1) Determine no circuito abaixo, utilizando Análise de Malhas, o valor da tensão V0. (3,0 PTS)
R.: V0 = 40V
2) Determine no circuito abaixo, utilizando Análise de Nodal, o valor da corrente I0. (3,0 PTS)
R.: I0 = 36A
3) Para o diagrama abaixo, calcule o valor da tensão V0, utilizando:
a) O Princípio da Superposição. (2,0 PTS)
b) O Teorema de Thévenin . (2,0 PTS)
R.: V0 = - 8V
Página 14 de 15
SIMULADO DE PROVA PROPOSTO (B)
1) Determine no circuito abaixo, utilizando Análise de Malhas, o valor da tensão V0. (3,0 PTS)
R.: V0 = -17,5V
2) Determine no circuito abaixo, utilizando Análise de Nodal, o valor da corrente I0. (3,0 PTS)
R.: I0 = 360A
3) Para o diagrama abaixo, calcule o valor da corrente I0, utilizando:
a) O Princípio da Superposição. (2,0 PTS)
b) O Teorema de Thévenin . (2,0 PTS)
R.: I0 = - 1A
Página 15 de 15