Filtros
{PhysicalOverview.doc}
Considere-se um sistema em cuja entrada se força uma onda,
s(t) = cos (2 π f t)
Recordando uma afirmação acima – e pressuposto (como se fará em todo este documento) que o sistema é
invariante-no-tempo e linear -, o sinal à saída reproduz “essa” onda, quando muito atenuando-a e atrasando-a:
cos (2 π f t) ⇒ G(f) cos (2 π f t - ϕ(f))
O ganho na amplitude, G(f), e o atraso de fase , ϕ(f), dependem da frequência da onda, f.
Quando o ganho varia com a frequência – isto é: não é constante, observando-se que algumas ondas aparecem
na saída mais atenuadas que outras -, obtém-se um assim denominado filtro. Os filtros com mais interesse são
aqueles que idealmente deixam passar uniformemente as frequências de alguma banda {flow … fhigh} – dita banda
de passagem (ou passante); relativamente às restantes frequências, que constituem a assim denominada banda de
rejeição, a atenuação advém mesmo muito elevada. Consoante os limites da banda passante, os Filtros classificamse em:
- Passa-Baixo: a atenuação é infinita para além duma frequência fcut, passam as frequências abaixo de fcut;
- Passa-Alto: a atenuação é infinita até uma frequência fcut, passam as frequências acima de fcut;
- Passa-Banda: passam apenas as frequências duma banda {fcuti … fcuts}, a atenuação é infinita fora dela;
- Elimina-Banda: a atenuação é infinita para alguma banda de frequências, {fcuti … fcuts}, apenas passam as
frequências fora dela;
fcut designa-se de frequência de corte; fcuti e fcuts designam-se de frequência de corte inferior e superior,
respectivamente.
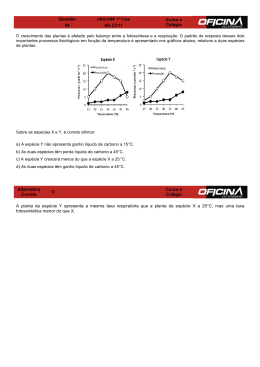
Ao lado, representa-se, para cada uma destas classes de filtros, a correspondente Resposta de Amplitude ideal,
G(f) = AmplitudeSaída/ AmplitudeEntrada.
(Quanto à Resposta de Fase ideal, já oportunamente se constatou que - na Banda passante - o atraso de fase deve
ser proporcional à frequência).
Os filtros ideais são irrealizáveis – no sentido de que não se consegue construir filtros em que, para uma
frequência de corte, fcut, a resposta de frequência sofra uma descontinuidade abrupta. Na prática, considerase frequência de corte aquela para a qual a relação entre as potências à saída e à entrada (normalizada por
essa relação na frequência central da banda passante) cai para 1/2 – ou, o que é o mesmo, o ganho de
amplitude normalizado vem a ser de √1/2 ≈ 0,707. Ademais, e continuando a observar filtros reais, a resposta
de amplitude não é constante na banda passante, e não é exactamente nula na banda de rejeição.
Existem muitas situações onde convém usar filtros. Exemplos são-no: a filtragem/supressão de sinais que
transportam ruído, interferências, distorção… Adiante, serão considerados diversos dispositivos (nomeadamente,
desmoduladores AM, multiplexers FDM) onde os filtros têm um papel de relevo.
Amplificadores / Decibel
{PhysicalOverview.doc}
Considere o leitor, por exemplo, dois sistemas {S1, S2}, de respostas na frequência {G1, ϕ1} e {G2, ϕ2},
acoplados em série – isto é: o sinal à entrada de S2 é o sinal a saída de S1. Qual será a resposta do conjunto?
Se à entrada de S1 se forçar uma onda, s1(t) = cos (2 π f t), à saída dele observar-se-á:
G1 cos (2 π f t - ϕ1).
Forçando este sinal à entrada de S2 (isto é: fazendo s2(t) = G1 cos (2 π f t - ϕ1)) à saída de S2 observar-se-á:
G2 G1 cos (2 π f t - ϕ1 - ϕ2).
A conclusão é: o conjunto dos dois sistemas em série exibe uma resposta em frequência de {G2 * G1, ϕ1 + ϕ2}.
Repare-se: o atraso de fase total logra-se com uma soma, ϕ1 + ϕ2, mas já o ganho total exige uma multiplicação,
G2 G1 – o que não é mesmo nada cómodo. Pelo que, na prática, se prefere um outro modo de agir: fazendo entrar
em cena uma unidade logarítmica (o decibel, dB) para exprimir o ganho.
Eis a definição de decibel: seja um sistema cujos sinais à entrada e saída têm as potências médias de,
respectivamente, PotênciaEntrada e PotênciaSaída; o ganho experimentado será, expresso em dBs:
GP = 10 log10 PotênciaSaída / PotênciaEntrada dB
Note-se: conquanto a Potência se exprima em Watt, o ganho – porquanto é relação entre Potências - é uma
grandeza essencialmente adimensional; o dB exprime tão somente que ela está expressa logaritmicamente.
Supondo potências dissipadas sobre resistências de 1 Ω, ter-se-á, em termos de Corrente ou Tensão:
GP = 10 log10 ISaída2 / IEntrada2 = 20 log10 ISaída / IEntrada dB
= 10 log10 VSaída2 / VEntrada2 = 20 log10 VSaída / VEntrada dB
Caso particular: na frequência de corte dum filtro, fcut - aquela em que o ganho de potência cai para
metade do ganho no centro da banda passante –, o ganho normalizado do filtro será 10 log10 1/2 = -3 dB.
Para aferir da vantagem do uso de dBs na facilitação dos cálculos, considere-se de novo o exemplo acima - dois
sistemas {S1, S2} em série - forçando ganhos de, por exemplo, -40 dB e 70 dB. Designando de PI1 e PI2 as potências
dos sinais à entrada dos sistemas, e PO1 e PO2 as potências dos sinais à saída, ter-se-á:
-40 = 10 log10 PO1 / PI1 dB → PO1 = 10-4 PI1;
70 = 10 log10 PO2 / PI2 dB → PO2 = 107 PI2;
Pois que os sistemas estão em série, PI2 = PO1, e por conseguinte:
PO2 = 107 * 10-4 PI1 = 103 PI1,
Isto é: o ganho do conjunto em série vem a ser GP = 10 log10 PO2 / PI1 = 30 dB – resultado a que se poderia ter
chegado muito mais simplesmente: somando algebricamente os ganhos individuais (em dB) dos sistemas:
GP Série = (-40) + (+70) = +30 dB.
Não haja confusões: se o ganho de, por exemplo, S1 é de -40 dB, isto é, 20 log10 VSaída / VEntrada = -40,
então a relação entre os sinais à saída e à entrada é de: VSaída / VEntrada = 10 -2 = 0,01.
Aplicações:
Os meios de transmssão atenuam os sinais transmitidos: parte da sua potência é dissipada no meio à medida que
eles se propagam.
No caso particular de meios guiados (linhas, coaxial e fibra óptica), a potência decresce exponencialmente com a
distância, d: PSaída / PEntrada = 10 -αd/10, em que α é o coeficiente de atenuação, em dB/km. Expressa em dB, a
atenuação após d km será então –αd: em dB, a atenuação é proporcional à distância! Por exemplo, um cabo de
fibra de 25 km com coeficiente de atenuação α=-0,4 dB/km provoca uma atenuação total de -0,4*25=-10 dBs.
Já no caso de meios não-guiados (os sinais são emitidos por antenas, e propagam-se em espaço livre: feixes
hertzianos, satélites, rádio), a potência decresce com o quadrado da distância: PSaída / PEntrada = (c/4πfd)2, em que f é
a frequência usada. Expressa em dBs, a atenuação após percorridos d km será então 20 log10(c/4πfd).
Quer num caso, quer noutro, usam-se, para compensar tal atenuação, amplificadores/repetidores – inseridos ao
longo do percurso (em geral, equidistantes). A distância entre eles deve ser tal que a potência do sinal não desça
tanto que ele acabe por se confundir com o ruído. Por cada secção amplificador+meio, a atenuação no fim será, em
dB, a soma algébrica do ganho do amplificador com a atenuação (um ganho negativo) do meio.