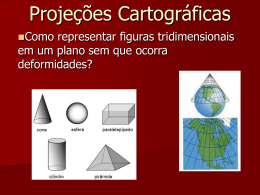
4. SISTEMAS DE PROJEÇÃO
4.1 Definição:
“São modelos geométricos ou analíticos
utilizados para representar sobre um plano
horizontal a superfície total ou parcial da terra.”
A representação plana da superfície terrestre é
uma necessidade para o manuseio através de
mapas terrestres.
Para a definição de um sistema de projeção
precisamos definir uma superfície de referencia
e uma superfície de projeção
SISTEMAS DE PROJEÇÃO
• PROBLEMA BÁSICO: representação de uma
superfície curva em um plano: representar a
Terra em um plano.
• Pode-se dizer que todas as representações
de superfícies curvas em um plano
envolvem: "extensões" ou "contrações" que
resultam em distorções ou "rasgos".
SISTEMA DE PROJEÇÃO IDEAL
1- Manutenção da verdadeira forma das áreas a
serem representadas (conformidade).
2- Inalterabilidade das áreas (equivalência).
3- Constância das relações entre as distâncias dos
pontos representados e as distâncias dos seus
correspondentes (eqüidistância).
As representações cartográficas são efetuadas, na sua
maioria, sobre uma superfície plana (Plano de
Representação onde se desenha o mapa).
4.2 CLASSSIFICAÇÃO DAS PROJEÇÕES
• Quanto ao Método de Construção
• Quanto a Superfície de Projeção
• Quanto às Propriedades
• Quanto ao Tipo de Contato entre a Superfície de
Referência e a Superfície de Projeção
CLASSIFICAÇÃO DAS PROJEÇÕES
CLASSSIFICAÇÃO DAS PROJEÇÕES QUANTO AO
MÉTODO DE CONSTRUÇÃO
Projeção Geométrica;
Se baseia em princípios geométricos projetivos. Dependendo
da localização do ponto de vista, as projeções geométricas
podem se subdividir em: Gnomônica: Ponto de vista no centro
da Terra. Estereográfica: Ponto de vista na superfície da Terra
e Ortográfica: Ponto de vista no infinito.
Projeções analíticas:
São aquelas que perderam o sentido geométrico propriamente
dito, em consequência da introdução de leis matemáticas.
Visando conseguir determinada propriedade.
Atualmente, quase todas a sprojeções cartográficas são
analíticas.
QUANTO A SUPERFÍCIE DE PROJEÇÃO
Plana
Cônica
Cilindrica
QUANTO A SUPERFÍCIE DE PROJEÇÃO
• PLANA
Este tipo de superfície pode assumir três
posições básicas em relação a superfície de
referência: polar, equatorial e oblíqua (ou
horizontal)
CLASSIFICAÇÃO A SUPERFÍCIE DE
REFERÊNCIA
• CÔNICA
Embora esta não seja uma superfície plana,
já que a superfície de projeção é o cone, ela
pode ser desenvolvida em um plano sem que
haja distorções, e funciona como superfície
auxiliar na obtenção de uma representação.
A sua posição em relação à superfície de
referência pode ser: normal, transversal e
oblíqua (ou horizontal).
POSIÇÕES DA SUPERFÍCIE DE PROJEÇÃO NA
PROJEÇÃO CÔNICA
POSIÇÃO DA SUPERFÍCIE DE PROJEÇÃO NA
PROJEÇÃO CILÍNDRICA
PROJEÇÃO CILÍNDRICA
• Tal qual a superfície cônica, a superfície de
projeção que utiliza o cilindro pode ser
desenvolvida em um plano e suas possíveis
posições em relação a superfície de
referência podem ser: equatorial, transversal
e oblíqua (ou horizontal).
CLASIFICAÇÃO DAS PROJEÇÕES QUANTO ÀS
PROPRIEDADES
Eqüidistantes: São as projeções que não apresentam
deformações lineares, ou seja, os comprimentos são
representados em escala uniforme. Esta condição so
e conseguida em determinada direção, podendo ser
classificadas ainda em: meridianas, transversais e
azimutais ou ortodromicas. Estas projeções são
menos empregadas que as projeções conformes ou
equivalentes, porque raramente e desejável um
mapa com distancias corretas apenas em uma
direção.
CLASSIFICAÇÃO DAS PROJEÇÕES QUANTO AS
PROPRIEDADES
Equivalentes: não deformam a área,
conservando uma relação constante em
termos de área, com a superfície terrestre..
Não sao adequadas a cartografia de base,
porem muito usadas na cartografia temática
CLASIFICAÇÃO DAS PROJEÇÕES QUANTO AS
PROPRIEDADES
• Conformes: também conhecidas como
ortomorficas, possuem a propriedade de não
deformar a forma e o ângulo de pequenas
áreas. Nestas projeções os paralelos e
meridianos se cruzam em ângulos retos, e a
escala em torno de um ponto se mantem
constante para qualquer direção. Uma das
projeções conformes mais conhecidas e a
Universal Transversa de Mercator ou UTM,
utilizada
no
mapeamento
sistemático
brasileiro.
CLASIFICAÇÃO DAS PROJEÇÕES QUANTO AS
PROPRIEDADES
• Afilática,
igualmente
conhecida
como
arbitrária, nos Estados Unidos, não possui
nenhuma das propriedades dos quatro tipo,
isto
é,
equivalência,
conformidade,
eqüidistância.Porém, este tipo de projeção
pode possuir uma ou outra propriedade que
justifique a sua construção. Por exemplo, a
gnômica, mesmo apresentando todas as
deformações,
possui
a
excepcional
propriedade de representar as ortodromias
retas.
CLASSIFICAÇÃO DE UMA PROJEÇÃO EM FUNÇÃO
DO TIPO DE CONTACTO ENTRE A SUPERFICIE DE
REFERÊNCIA E SUPERFÍCIE DE projeção
Projeção
Classificação
Aplicações
Características
Albers
Cônica
Equivalente
Mapeamentos temáticos. Serve para
mapear áreas com extensão predominante
leste-oeste.
Preserva áreas.
Substitui com vantagens todas as outras
cônicas equivalentes.
Bipolar
Cônica
Conforme
Indicada para base cartográfica confiável
dos continentes americanos.
Preserva ângulos.
É uma adaptação da Cônica de Lambert.
Cilíndrica
Equidistant
e
Cilíndrica
Equidistante
Mapas Mundi.
Mapas em escalas pequenas.
Trabalhos computacionais.
Altera áreas.
Altera ângulos.
Gauss
Cilíndrica
Conforme
Cartas topográficas antigas.
Mapeamento básico em escala média e
grande.
Altera áreas (mas as distorções não
ultrapassam 0,5%).
Preserva ângulos.
Similar à UTM com defasagem de 3 de
longitude entre os meridianos centrais.
Estereográf
ica Polar
Plana
Conforme
Mapeamento das regiões polares.
Mapeamento da Lua, Marte e Mercúrio.
Preserva ângulos.
Oferece distorções de escala.
Lambert
Cônica
Conforme
Cartas gerais e geográficas.
Cartas militares.
Cartas aeronáuticas do mundo.
Preserva ângulos.
Lambert
Million
Cônica
Conforme
Cartas ao milionésimo.
Preserva ângulos.
Mercator
Cilíndrica
Conforme
Cartas náuticas.
Cartas geológicas e magnéticas.
Mapas Mundi.
Preserva ângulos.
Miller
Cilíndrica
Mapas Mundi.
Mapas em escalas pequenas.
Altera ângulos.
Altera áreas.
Plana
Armazenamento de dados que não se encontram vinculados a
qualquer sistema de projeção convencional (desenhos, plantas,
imagens brutas ou não georeferenciadas, etc.).
Sistema local de coordenadas
planas.
Cônica
Mapeamento temático em escalas pequenas.
Altera áreas e ângulos.
Substituída pela Cônica
Conforme de Lambert nos
mapas mais atuais.
Latlong
-
Aramazenamento de dados matriciais com resolução espacial
definida em graus decimais.
Geometria idêntica a da
projeção cilíndrica
equidistante.
Sinusoidal
Pseudocilíndrica
Equivalent
e
Mapeamentos temáticos em escalas intermediárias e pequenas.
Preserva áreas.
UTM
Cilíndrica
Conforme
Mapeamento básico em escalas médias e grandes.
Cartas topográficas.
Preserva ângulos.
Altera áreas (mas as distorções
não ultrapassam 0,5%).
No_Project
ion
Policônica
4.3 O SISTEMA UNIVERSAL TRANSVERSO
DE MERCATOR – UTM
Conhecida não como uma projeção, mas como
um sistema da projeção transversa de
Mercator( conforme de Gauss). Surgiu o
sistema em 1947, para determinar as
coordenadas retangulares nas cartas militares,
em escala grande, de todo mundo.
No Brasil, a maioria das cartas confeccionadas
por Levantamentos Aerofotogramétricos, é
executada utilizando este sistema de projeção.
Projeção cilíndrica, conforme.
SISTEMA UTM
• Um cilindro secante à superfície de referência (eixo
do cilindro no plano do Equador), com diâmetro
menor do que o diâmetro da superfície de referência,
criando, assim, duas linhas de interseção entre o
cilindro e a sup. de referência. Essa área é chamada
de FUSO ou ZONA.
4.3.1 CARACTERÍSTICAS DA PROJEÇÃO UTM
• A superficie de projeção é um cilindro transverso e a
projeção é conforme
• O meridiano central da região de interesse, o
equador e os meridianos situados a 90graus do
meridiano central são representados por retas
• Os outros meridianos e paralelos são curvas
complexas
• A escala aumenta com a distancia em relação ao
meridiano central. A 90 graus deste, a escala tornase infinita
CARACTERÍSTICAS DA PROJEÇÃO UTM
• O meridiano central é o meridiano intermediário aos
dois meridianos secantes ao cilindro. No meridiano
central, o fator de redução de escala (ko) é de 0,9996
originado pela particularidade da secância do cilindro
e elipsóide.
• A partir do meridiano central, o fator cresce para
leste e oeste até atingir o valor 1 nas linhas de
secância (aproximadamente 1°37' a partir do
meridiano central) e continua a crescer até atingir
1,0010 nas bordas do fuso (3° do meridiano central).
Nos meridianos secantes, a distorção é nula e esta
linha meridiana é chamada de Linha de Distorção
Zero (LDZ).
CARACTERÍSTICAS DO SISTEMA UTM
• A Terra e dividida em 60 fusos de 6 graus de largura,
numerados a partir do anti-meridiano de Greenwich(
meridiano de longitude 180°), seguindo de oeste para
leste ate o fechamento neste mesmo ponto de origem.
•Cada fuso possui um meridiano central (MC)que o
divide exatamente ao meio, sendo o seu valor igual ao
do limite inferior do fuso mais 3 graus
UTM
Cada fuso é representado pelo número do fuso ou pela
longitude do meridiano central
CARACTERÍSTICAS DA PROJEÇÃO UTM
• Para evitar coordenadas negativas, é atribuído o
valor 500.000 m ao meridiano central. Assim, para os
6° de amplitude do fuso, o eixo E varia de
aproxidamente 160.000 m até 840.000 m para cada
fuso.
• Para o eixo N, a referência é o equador e o valor
atribuído depende de hemisfério. Quando tratamos
de regiões no hemisfério norte, o equador tem um
valor de N igual a 0 m. No hemisfério sul, o equador
tem um valor N igual a 10.000.000 m.
• Designação das coordenadas plano-retangulares
pelas letras N e E (respectivamente ordenada e
abscissa)
SISTEMA DE COORDENADAS
As coordenadas UTM são
expressas em metros. O
eixo E (Easting) representa
a coordenada no sentido
leste-oeste.
O
eixo
N
(Northing)
representa a coordenada
no sentido norte-sul.
CARACTERÍSTICAS DA PROJEÇÃO UTM
No sentido Norte-Sul, a divisão é feita em segmentos de
8°. A nomenclatura é usada somente entre os paralelos
84° N e 80° S, começando a 80° S, com a letra C até a
•letra X. As letras I e O são omitidas porque podem ser
confundidos com números. A distorção nos pólos é
muito grande na projeção UTM. assim para os pólos,
usa-se a Projeção Universal Polar Estereográfica
(UPS).
SISTEMA UTM
FUSOS QUE COBREM O TERRITÓRIO BRASILEIRO
APLICAÇÕES DA PROJEÇÃO UTM
Indicada em regiões de predominância na
extensão Norte-Sul entretanto mesmo na
representação de áreas de grande longitude
poderá ser utilizada.
É a mais indicada para o
topográfico a grande escala, e é
Projeção adotado para o
Sistemático Brasileiro. Utilizado
de1:250.000 até 1:25.000.
mapeamento
o Sistema de
Mapeamento
nas escalas
4.3.2 CONCEITOS FUNDAMENTAIS NO SISTEMA
UTM
• I)Norte Verdadeiro ou de Gauss: Com
direção tangente ao meridiano (geodésico)
passante pelo ponto e apontando para o Polo
Norte.
• II)Norte da Quadrícula:
Com direção
paralela ao eixo N (que coincide com o
Meridiano Central do fuso) do Sistema de
Projeção UTM no ponto considerado e
apontando para o Norte.
CONCEITOS FUNDAMENTAIS
• III) Azimute: É o ângulo formado entre a direção
Norte-Sul e a direção considerada, contado à
partir do Polo Norte, no sentido horário. O
azimute varia de 0º a 360º e dependendo do Norte
ao qual esteja referenciado podemos Ter:
Azimute Verdadeiro ou Gauss
Azimute da Quadrícula ou plano
Azimute Magnético
• Obs.: o azimute geodésico corresponde ao
azimute verdadeiro contato a partir do Polo Sul.
4.3.3 CONVERGÊNCIA MERIDIANA
4.3.3.1 Definição
A convergência meridiana é o ângulo C, que num
determinado ponto P é formado pela tangente ao
meridiano deste, e a paralela ao meridiano central.
CONVERGÊNCIA MERIDIANA
Onde: NQ => Norte da quadrícula
C => Convergência meridiana
MC => Meridiano central
Sinal da convergência meridiana
C => é positiva quando o ponto estiver a oeste do
meridiano central
C => é negativa quando o ponto estiver a leste do
meridiano central
No hemisfério norte há inversão do sinal.
4.3.3.2 IMPORTÂNCIA DA CONVERGÊNCIA
MERIDIANA
• A convergência meridiana é utilizada para
transformar o azimute verdadeiro, determinado via
astronomia, em azimute plano (norte da quadrícula)
e vice-versa.
• O azimute plano é utilizado em Geodésia para
cálculos das coordenadas planas sistema UTM (E,
N).
• O azimute verdadeiro é utilizado em Topografia para
cálculos das coordenadas locais (X, Y).
FORMULÁRIO PARA O CÁLCULO DA CONVERGÊNCIA
MERIDIANA EM FUNÇÃO DAS COORDENADAS GEOGRÁFICAS
C = XII.p + XIII.p3 + C’5.p5
Onde:
p = 0,0001.
 = MC - 
central do fuso.
onde MC é a longitude do meridiano
XII = sen.104
sen 2 1" sen  cos2 
1  3e'2 cos2   2e'4 cos4  .1012
XIII 
3
sen 4 1" sen  cos4 
2  tg 2 .10 20
C' 5 
15
CÁLCULO DA LONGITUDE DO MERIDIANO
CENTRAL
a)Para pontos de longitude Oeste
a.1)Número do Fuso
180  
Nf 
6
a.2)Longitude do Meridiano Central
MC  módulo (180  6.Nf )  3
B) Para pontos de Longitude Leste
b.1) Número do Fuso

Nf   30
6
b.2)Longitude do Meridiano Central
MC  6.( Nf  30)  3
DETERMINAÇÃO DO MERIDIANO CENTRAL
•Exemplo 1
Determinar a longitude do meridiano central para o ponto de
longitude   7820'40"W
180  7820'40"
Nf 
 16,9....  fuso 17
6
MC  módulo(180 - 6x47)  3  81
Exemplo 2:
Determinar a longitude do meridiano central para o ponto de
longitude   13545'10"
Nf 
13545'10"
 30  52,6....  fuso 53
6
MC  6(53  30)  3  135
FORMULÁRIO PARA O CÁLCULO DA
CONVERGÊNCIA MERIDIANA EM FUNÇÃO DAS
COORDENADAS PLANAS –SISTEMA UTM
C  (XV)q  (XVI)q 3  F'5 q 5
q  0,000001E
tg ' 1 6
XV 
10
Nsen1" K 0
E'  módulo(500.000  E)
K 0  0,9996(fator de escala)
tg '
1
2
2
2
4
4
18
XVI 
(1

tg


e'
cos


2e'
cos

)
10
3
3N 3sen1"
K0
tg '
1
2
4
30
F'5 
(2

5tg

'

3tg

'
)
10
5
15N 5sen1"
K0
CÁLCULO DA CONVERGÊNCIA MERIDIANA
Cálculo de  '
1
α
 i1  (B' i βsen2 i  γsen4 i  δsen6 i  εsen8 i  ξsen10 i )
A.a(1  e 2 )
α
ρ0
B.a(1  e )
2
D.a(1  e 2 )
δ
6
β
2
ρ0 
180
 57,29577951310
π
C.a(1  e 2 )
γ
4
E.a(1  e 2 )
ε
8
F.a(1  e 2 )
ξ
10
O valor inicial para  ' será dado por :
N' 1
 '1 
0,9996 α
N'
B' 0 
K0
4.3.3 TRANSFORMAÇÃO DE COORDENADAS
GEOGRÁFICAS EM PLANAS
FORMULÁRIO
N = N’+10.000.000,
E = 500.000 +E’.
N’= I+IIp2 +IIIp4+A’6p6
E’= IVp + Vp3 + B5
a) Cálculo da Coordenada N (ordenada):
I= B.K0 onde K0= 0,9996
B é o comprimento do arco de meridiano que vai do Equador até o ponto.
N.sen .cos .sen21.
II 
K 0 .108
2
sen 41".N.sen .cos3
III 
(5  tg 2  9e'.cos2  4e' 4 cos4 ).K0 .1016
24
A' 6 
sen 61" Nsen .cos5
p  0,0001"
(61  58 tg2  tg 4  270 e'2 cos2  320 e'2 sen 2 )K0 .1024
    MC
TRANSFORMAÇÃO DE COORDENADAS
GEOGRÁFICAS EM PLANAS
IV  Ncossen1".K 0 .104
sen 31".Ncos3
V
(1  tg 2  e' 2 cos2 )K 0 .1012
6
sen 51" Ncos5
B' 5 
(5  18tg 2  tg 4  14e' 2 cos2  58e' 2 sen 2 ).K0. .1020
120
e' na fórmula, representa a segunda excentricidade