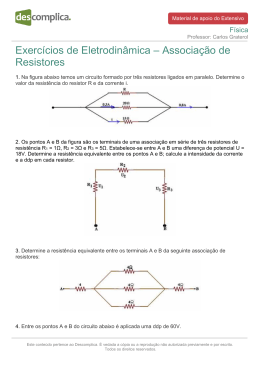
Conceitos
“O mundo do aprendizado é tão amplo
e a alma humana, tão limitada!
Quebramos a cabeça para puxar apenas
uma pontinha da cortina que cobre o
infinito.”
Maria Mitchell
Resistor: Dispositivo elétrico cuja função é a dissipação da energia elétrica em calor, desta forma
controlando a intensidade da corrente elétrica. Nos esquemas de circuito os resistores são representados
pelos símbolos abaixo:
ou
1. Código de cores de um resistor: A imagem abaixo mostra um resistor e o código de cores que
identifica sua resistência.
A figura a seguir mostra um exemplo da leitura de resistências a partir do código de cores.
Física – Ciências da Computação – 2.o sem/2009 - Aula 3 - pág.1/5
A figura a seguir mostra a tabela de código de cores de resistência.
2. Associação de resistores: Uma associação de resistores é um conjunto de resistores operando
simultaneamente em um mesmo circuito elétrico. Para qualquer associação é verdadeira a
propriedade de que a potência da associação é a soma das potências dos componentes, ou seja,
Passociação = Pcomponente. Fundamentalmente são dois tipos de associação, a série e a paralela.
Física – Ciências da Computação – 2.o sem/2009 - Aula 3 - pág.2/5
3. Associação em série: Dois ou mais resistores estão associados em série se são percorridos pela
mesma corrente elétrica.
Propriedades:
i = constante
Usérie = Ucomponente
4. Associação em paralelo: Dois ou mais resistores estão associados em paralelo se são submetidos à
mesma tensão.
Propriedades:
U = constante
isérie = icomponente
5. Resistor equivalente: é o resistor que sozinho dissipa tanta potência quanto uma associação de
resistores.
6. Resistor equivalente de uma associação em série: Sabemos que para qualquer associação a potência
equivalente é igual a soma das potências componentes. Então:
Psérie = Pcomponente
(U.i)série = (U.i)componente
Como i é constante
i.Usérie = i.Ucomponente
Usérie = Ucomponente
(R.i)série = (R.i)componente
Como i é constante
i.Rsérie = i.Rcomponente
Rsérie = Rcomponente
Física – Ciências da Computação – 2.o sem/2009 - Aula 3 - pág.3/5
7. Resistor equivalente de uma associação em paralelo: Sabemos que para qualquer associação a
potência equivalente é igual a soma das potências componentes. Então:
Pparalelo = Pcomponente
(U.i)paralelo = (U.i)componente
Como U é constante
U.iparalelo = U.icomponente
iparalelo = icomponente
(U/R)paralelo = (U/R)componente
Como U é constante
U.(1/R)paralelo = U.(1/R)componente
(1/R)paralelo = (1/R)componente
8. Resistor equivalente de uma associação em paralelo (Casos particulares)
a) Se a associação paralela for composta por apenas dois resistores pode-se escrever:
1/Rparalelo = 1/R1 + 1/R2 = (R1 + R2)/(R1.R2)
Rparalelo = (R1.R2)/ (R1 + R2)  mnemonicamente  Rparalelo = produto/soma
b) Se a associação paralelo for composta por n resistores idênticos pode-se escrever:
1/Rparalelo = 1/R +1/R +1/R +1/R +1/R +1/R +...+1/R = n/R
Rparalelo = R/n
Obs.: O resistor equivalente a uma associação paralela é sempre MENOR que o menor dos
componentes.
Exercícios:
1. Associam-se dois resistores em série, sendo R1 = 10  e R2 = 15 . A d.d.p. entre os extremos da
associação é de 100 V. Determine: a) a resistência equivalente à associação; b) a intensidade da
corrente que atravessa cada resistor; c) a ddp em cada resistor.
Resolução:
a) Rsérie = 10 + 15 = 25
b) i = U/R = 100/25 = 4A
c) U1 = R1.i = 10.4 = 40V
U2 = R2.i = 15.4 = 60V
2. Associam-se dois resistores em série, sendo R1 = 25  e R2 = 35 . A d.d.p. entre os extremos da
associação é de 180 V. Determine: a) a resistência equivalente à associação; b) a intensidade da
corrente que atravessa cada resistor; c) a ddp em cada resistor.
3. Dois resistores de resistências 4,0  e 6,0  são associados em série. A ddp medida entre os
terminais do resistor de 4,0  é de 24 V. Determine: a) a intensidade da corrente que atravessa os
resistores; b) a ddp entre os terminais do resistor de 6,0 ; c) a ddp entre os terminais da associação;
d) a resistência equivalente à associação.
4. Dois resistores, um de 6,0  e outro de 3,0 , são associados em paralelo. O conjunto é submetido à
tensão de 12 V. Determine: a) a resistência equivalente; b) a intensidade de corrente em cada
resistor; c) a intensidade de corrente que atravessa a associação; d) a potência dissipada pela
associação.
Resolução:
a) Rparalelo = (6.3)/(6+3) = 18/9 = 2
b) i1 = U/R1 = 12/6 = 2A
i2 = U/R2 = 12/3 = 4A
c) i = U/R = 12/2 = 6A
d) P = U.i = 12.6 = 72W
5. Dois resistores, um de 9,0  e outro de 4,0 , são associados em paralelo. O conjunto é submetido à
tensão de 72 V. Determine: a) a resistência equivalente; b) a intensidade de corrente em cada
resistor; c) a intensidade de corrente que atravessa a associação; d) a potência dissipada pela
associação.
Física – Ciências da Computação – 2.o sem/2009 - Aula 3 - pág.4/5
6. Três resistores estão associados em paralelo. Dois deles valem 10  e 15 , respectivamente. O
resistor de 15  é atravessado por uma corrente de 10 A, enquanto que o terceiro resistor,
inicialmente desconhecido, é percorrido por uma corrente de 25 A. Determine: a) a resistência do
terceiro resistor; b) a intensidade de corrente que atravessa o resistor de 10 ; c) a resistência
equivalente à associação; d) a potência dissipada pela associação.
7. Dois resistores de 8,0  e 2,0  estão associados em paralelo. A corrente que atravessa a associação
é de 2,0 A. Determine a corrente em cada resistor.
Resolução:
Rparalelo = (8.2)/(8+2) = 16/10 = 1,6
U = R.i = 1,6.2 = 3,2V
i1 = U/R1 = 3,2/8 = 0,4 A e i2 = 2 - 0,4 = 1,6 A.
8. Dois resistores de 10  e 4,0  estão associados em paralelo. A corrente que atravessa a associação
é de 3,0 A. Determine a corrente em cada resistor.
9. Determinar o resistor equivalente a uma associação paralela na qual os componentes são 2,0 , 3,0
 e 5,0 .
Resolução:
1/Rparalelo = (1/R)componente
1/Rparalelo = 1/R1 +1/R2 +1/R3
1/Rparalelo = 1/2 +1/3 +1/5
1/Rparalelo = 0,50 +0,33 +0,20 = 1,03  Rparalelo = 1/1,03 = 0,97
Obs.: Neste caso não podemos utilizar a regra mnemônica de produto sobre soma, pois são três os
resistores envolvidos e não apenas dois.
Claro que é possível, ainda que logo, fazer o problema de modo associativo, pois:
R’paralelo = (2.3)/(2+3) = 6/5 = 1,20
Rparalelo = (1,20.5)/(1,20+5) = 6/(6,20) = 0,97
E veja que o problema é comutativo, pode ser realizado em outra ordem, pois:
R’paralelo = (3.5)/(3+5) = 15/8 = 1,88
Rparalelo = (1,88.2)/(1,88+2) = 3,76/3,88 = 0,97
10. Três resistores estão associados. Dois deles possuem valores conhecidos, a saber, 5,0  e 4,0 . O
resistor de 5,0  é colocado em série com o terceiro resistor e este fio é associado em paralelo com o
resistor de 4,0 . Sabe-se que a associação final possui resistência equivalente a 3,0 . Determine o
valor do terceiro resistor.
11. Os lados de um triângulo, de vértices A, B e C, são formados por resistores, todos iguais a 10 
cada. Dado que os terminais da associação são os vértices A e C, determine o resistor equivalente à
associação.
12. Considere um quadrado de vértices A, B, C e D, no sentido horário. Cada lado é formado por um
resistor de 60  cada. Se os terminais do circuito são os vértices A e D, determine a resistência
equivalente à associação.
13. Refaça o item anterior, considerando que os terminais são os pontos A e C.
14. Considere um pentágono de vértices A, B, C, D e E, no sentido horário. Cada lado é formado por um
resistor de 72 cada. Se os terminais do circuito são os vértices A e E, determine a resistência
equivalente à associação.
15. Refaça o item anterior, considerando que os terminais são os pontos A e D.
Física – Ciências da Computação – 2.o sem/2009 - Aula 3 - pág.5/5