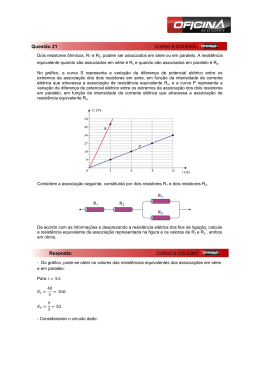
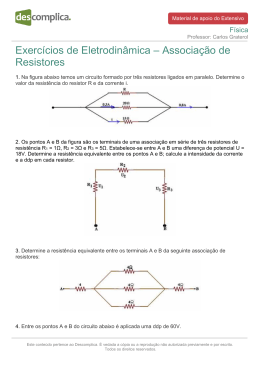
Física Aplicada
Eletricidade
3
Associação Série de Resistores
Associação Série de Resistores


Resistores estão ligados em série quando
a corrente que passa por um for a
mesma que passa pelos outros.
A Fig01 mostra um exemplo de ligação em
série e o resistor equivalente(RE).
Chamamos de resistor equivalente a um
único resistor que
pode substituir a
associação e mesmo assim
a corrente
fornecida pelo gerador será a mesma
Associação Série de Resistores
Fig01: Associação série de resistores - Circuito total e circuito equivalente
Associação Série de Resistores




Na Fig01 observe que o instrumento indica 2mA tanto no
circuito original como no equivalente (RE=6K).
Em uma associação em série o equivalente é dado por :
RE = R1 + R2 +R3
a) No caso de resistores iguais em série , o equivalente será
dado por :
RE = n.R , onde n é o número de resistores de valor R em
série.
b) O equivalente de uma associação série será sempre
maior que o maior dos resistores da associação .
Associação Série de Resistores


Outra característica de uma ligação em série é
que a soma das tensões nos resistores é igual à
tensão total, no caso da Fig01 , 12V.
A Fig02 mostra a tensão em cada resistor . Esta
é uma característica genérica de toda malha (
caminho fechado ) enunciada pela 2ª Lei de
Kirchhoff da seguinte forma: " A soma das
tensões orientadas no sentido horário é igual à
soma das tensões orientadas no sentido anti
horário ".
Associação Série de Resistores
Fig02: Associação série - Verificação da 2ª Lei de Kirchhoff
Na Fig02 : U4 = U1+U2+U3
que é a equação da malha do circuito
Exercícios

Qual a indicação dos instrumentos no
circuito a seguir ?
Resolução

R: Primeiro devemos calculara a
resistência equivalente
RE = R1+R2+R3+R4
= 200 + 500+1000+1300 = 3000= 3 K
 Em seguida devemos calcular a
corrente no resistor equivalente , a qual
será igual à corrente no circuito original:
I = 12V/3K = 4mA.
Resolução





Como a corrente no equivalente é igual à corrente
nos resistores da associação, então podemos
calcular a tensão em cada um : U1=200.4mA =
0,2K.4mA = 0,8V = 800mV
U2= 500W.4mA =0,5K.4mA = 2V
U3=1K.4mA = 4V
U4 = 1,3K.4mA = 5,2V
Observe que : U1+U2+U3+U4 = 12V
Resolução

U = U1+U2+U3+U4 = 12V
 RE = R1+R2+R3+R4 = 3k
 U = R I  I = U/R = 4mA
Exercicio2:

Qual a potência dissipada em cada
resistor no exercício 1 ? Qual a
potência elétrica do gerador ?
Resolução







R: Como já visto a potência dissipada em um
resistor é dada por: P =R.I2 ou P=U2 /R ou P=U.I
então : P1 = 0,8V.4mA = 3,2mW
P2 =2V.4mA = 8mW
P3 = 4V.4mA = 16mW e
P4 = 5,2V.4mA = 20,8mW
A potência que o gerador está fornecendo ao
circuito deve ser igual à soma das potências
dissipadas em cada resistor ou
P = U.I = 12V.4mA = 48mW
Associação Paralelo de Resistores

Resistores estão ligados em paralelo
quando a tensão aplicada em um for a
mesma aplicada nos outros.
A Fig03 mostra um exemplo de ligação paralelo
e o resistor equivalente(RE).
Fig03: associação paralelo - Circuito e resistor equivalente
No caso de uma associação paralelo o
resistor equivalente é calculado por:



1/RE = 1/R1 +1/R2 +1/R3 ou
em termos de condutância
( G = 1/R) GE = G1 + G2 + G3
Associação Paralelo de Resistores





a) Para dois resistores em paralelo a expressão
acima se reduz para:
RE =(R1.R2)/(R1+R2)
b) No caso de resistores iguais em paralelo :
RE =R/n , onde n é o numero de resistores de
valor R em paralelo.
c) O equivalente de uma associação paralelo
será sempre menor que o menor dos resistores
da associação
Associação Paralelo de Resistores

Na Fig03 observe que o instrumento indica 4mA tanto no
circuito original como no equivalente (RE=3K).

Outra característica de uma ligação paralelo é que a soma
das correntes nos resistores é igual à corrente total que
entra na associação, que é basicamente a 1ª Lei de
Kirchhoff que tem o seguinte enunciado:

" A soma das correntes que chegam em um nó ( 4mA ) é
igual à soma das correntes que dele saem ( 1,2mA +0,8mA
+2mA ) ".
Exercício 3: Na Fig03 calcule a potência dissipada em
cada resistor da associação e a potência elétrica do
gerador.





R: Novamente , para calcular a
potência de um bipolo basta fazer o
produto U.I, então:
P1= 12V.1,2mA = 14,4mW
P2 =12V.0,8mA = 9,6mW
P3 =12V.2mA = 24mW
P gerador = 12V.4mA = 48mW
Associação Paralelo de Resistores

Novamente observe que a soma das
potências dissipadas deve ser igual à
potência elétrica do gerador ( isso se
chama de conservação de energia ).
As seguir aplicações práticas de
circuitos paralelos:


Uma das principais aplicações de circuitos
paralelos
é
uma
instalação
elétrica residencial, a qual consiste de
lâmpadas , tomadas ligadas em paralelo.
A Fig04 mostra duas lâmpadas ligadas em
paralelo e acionadas por interruptores.
A Fig04 mostra duas lâmpadas ligadas em
paralelo e acionadas por interruptores.
Associação Paralelo de Resistores



Observe na Fig04 que, estando ligada
apenas uma lâmpada a corrente no fusível
será igual a 481mA.
O que acontece se a outra lâmpada
também for ligada?
Se as duas lâmpadas forem iguais o
consumo de corrente dobrará !!
Fig05: Lâmpadas ligadas em
paralelo - 2 lâmpada ligadas
Associação Paralelo de Resistores


Como você pode verificar a corrente dobra
de valor .
Quanto mais lâmpadas ( ou outro
dispositivo, tal como TV, chuveiro , etc )
estiverem ligados maior a corrente , e
maior o consumo !!