Universidade do Grande Rio “Prof. José de Souza Herdy”
UNIGRANRIO
WILLIS SUDÁRIO DE LIMA NETO
O ensino interdisciplinar entre Física e Matemática: Uma nova estratégia
para minimizar o problema da falta dos conhecimentos Matemáticos no
desenvolvimento do estudo da Física
Duque de Caxias
2011
APOSTILA DE TERMOLOGIA
(PROF. Willis Sudário)
Algumas Definições Fundamentais
1ªTemperatura: Medida do nível de agitação térmica das partículas ou medida do nível da
energia térmica média por partícula de um corpo ou sistema físico.
(((O))) (((O))) (((O)))
(((O))) (((O))) (((O)))
(((O))) (((O))) (((O)))
Maior agitação térmica
(Temperatura mais alta)
(O)
(O)
(O)
(O)
(O)
(O)
(O)
(O)
(O)
Menor agitação térmica
(Temperatura mais baixa)
2ª Calor: Energia térmica em transito devido a diferença de temperatura; flui do sistema de
temperatura mais alta para o de temperatura mais baixa até que ocorra o equilíbrio
térmico.
OBS: Pode-se falar em energia térmica de um corpo, porém jamais em calor de um corpo,
pois o calor não pode estar contido num corpo.
3ª Equilíbrio Térmico: Iguais temperaturas, isto é, mesmo nível de agitação térmica.
Assim, dois corpos em equilíbrio térmico possuem obrigatoriamente temperaturas iguais.
4ª Lei Zero da Termodinâmica: Se dois corpos A e C estiverem em equilíbrio térmico com
um terceiro corpo B, então A e C estarão em equilíbrio térmico entre si.
TERMOMETRIA
Graduação de um termômetro.
Qualquer pessoa pode criar uma escala termométrica, basta seguir alguns
passos.
1º) Escolhem-se dois sistemas cujas temperaturas sejam invariáveis ao longo do tempo e
que possam ser atingidas com certa facilidade. Estes pontos são chamados pontos fixos,
geralmente usam-se a temperatura do gelo e a temperatura do vapor.
2º) O termômetro é colocado na presença dos dois sistemas definidos como pontos fixos.
A cada um deles ira corresponder uma altura da coluna de mercúrio. A cada uma das
alturas atribui-se um valor numérico arbitrário.
3º) O intervalo entre as marcações feitas é dividido em partes iguais, chamado de unidade
da escala (grau).
ESCALAS TERMOMÉTRICAS
Existem 3 escalas termométricas mais usadas.
Celsius – Escala criada em 1742, pelo astrônomo sueco Anders Celsius. Foi criada
escolhendo o valor de 0ºC para a temperatura do gelo e de 100ºC para a temperatura do
vapor. O intervalo entre estes pontos fixos é dividido em 100 partes iguais. Esta escala é
usada em praticamente todo o mundo, com exceções de alguns paises como EUA.
Fahrenheit – Escala criada em 1724, pelo físico alemão Daniel Gabriel Fahrenheit. Nesta
escala adotou-se o valor de 32ºF para a temperatura para a temperatura do gelo e de
212ºF para a temperatura do vapor. O intervalo entre estes pontos fixos é dividido em 180
partes iguais. Esta escala é usada principalmente nos EUA.
Kelvin – Escala criada em 1848, pelo físico inglês conhecido como Lorde Kelvin. Nesta
escala adotou-se o valor de 373 K para a temperatura para a temperatura do gelo e de 273
K para a temperatura do vapor. O intervalo entre estes pontos fixos é dividido em 100
partes iguais. Esta escala é usada em trabalhos científicos e é a unidade de temperatura
do sistema internacional de medidas.
CELSIUS
FAHRENHEIT
KELVIN
OBS: A escala Kelvin é a onde esta a menor temperatura que se poderia imaginar: o zero
absoluto, que equivale a – 273 ºC, temperatura onde qualquer movimentação de
molecular cessa. Esta escala é conhecida como escala absoluta.
Porém para um estudo adequado desse conteúdo, precisamos de algumas definições
matemáticas que servirão de apoio na resolução de alguns exercícios. Caso você tenha
esquecido estas ferramentas serão revisadas agora.
Revisando Matemática – Razões e proporções
Considere a seguinte situação problema:
No vestibular para o curso de Matemática, havia 60 vagas para um total de 300
candidatos. Se compararmos estes valores através de uma simples divisão, teremos:
vagas
60 1
=
= , o que podemos concluir é que existe 1 vaga para cada 5 candidatos
candidatos 300 5
ou ainda, 5 candidatos para 1 vaga.
Quando comparamos dois números através de uma divisão, como fizemos acima diremos
que foi feita a RAZÃO entre estes dois números.
Definição:
Sendo a e b dois números racionais, com b ≠ 0 , denomina-se razão entre a e b ou razão
a
de a para b, a divisão .
b
a
é lida “razão de a para b”, onde o a é chamado de antecedente e o b de
b
conseqüente.
A razão
Exemplo: Em uma prova de Física com 20 questões Marcelo acertou 12 questões, nessas
condições responda:
a) Qual a razão de acertos e o total da prova de Marcelo?
acertos 12 3
=
= (a cada 5 questões da prova ,ele acertou 3)
total
20 5
b) Qual a razão de acertos e erros da prova de Marcelo?
acertos 12 3
=
= (a cada 3 questões certas, ele errou 2)
erros
8 2
Algumas razões especiais.
1º) Densidade demográfica: Expressão o número de habitantes por metro quadrado de
uma região. É dada pela razão entre o número de habitantes e a área da região
considerada.
Densidade demográfica =
N º de habi tan tes
área
2º) Escala: Razão entre duas grandezas que determina a redução ou a ampliação de
determinadas figuras.
escala =
comprimento do desenho
comprimento real
3º) Densidade de um corpo: É a razão entre a massa de um corpo e seu volume.
densidade =
massa do corpo
volume do corpo
4º) Velocidade Média: É a razão entre a distancia percorrida e o tempo gasto para
percorrê-la.
Velocidade média =
Distância percorrida
Tempo gasto
Proporções
Considere a seguinte situação problema:
João foi ao shopping comprar jogos para seu Playstation 3. O vendedor fez a seguinte
proposta, para cada 3 jogos que você comprar você terá 90 reais de desconto.
Podemos notar que o desconto será proporcional à quantidade de jogos que João
comprar, de acordo com a tabela:
Jogos
3
6
9
12
Desconto
90,00
180,00
270,00
360,00
Podemos notar ainda que a razão entre a quantidade de jogos e o total de desconto é
sempre o mesmo.
3
6
9
12
=
=
=
90 180 270 360
A igualdade entre duas razões é chamada de proporção.
Definição: Proporção é a igualdade entre duas razões. Assim, dados 4 números a, b, c e
a c
d, representamos a proporção =
e lemos: a está para b assim como c está para d.
b d
1º termo 3º termo
Os termos de uma proporção são dispostos na ordem:
onde, o 1º e o 4º
=
2º termo 4º termo
termos são os extremos e o 2º e o 3º são os meios.
Propriedade Fundamental das proporções.
Em uma proporção, o produto dos meios é igual ao produto dos extremos.
Seja a proporção
a c
= ⇒ a.d = b.c .
b d
Razão entre segmentos
Considere dois segmentos AB de 3u e BC de 9u, onde u é uma unidade de medida
qualquer. (m, cm, mm e etc.)
Verificando a razão entre AB e BC , temos:
AB 3u 1
=
=
BC 9u 3
Portanto, BC é 3 vezes maior que AB .
Definição:
A razão entre dois segmentos é a razão de suas medidas, tomadas na mesma unidade.
AB
.
Dados dois segmentos AB e BC , a razão entre eles indicada por
BC
Teorema de Tales
Vamos considerar um feixe de retas paralelas com duas transversais, como na figura.
- São correspondentes os pontos: A e A’, B e B’, C e C’ e D e D’.
- São correspondentes os segmentos: AB e A' B ' , BC e B' C ' , CD e C ' D' , AC e A' C ' e
etc.
Definição:
- Um feixe de retas paralelas determina sobre duas transversais segmentos proporcionais.
Ou ainda: Se duas retas são transversais de um feixe de retas paralelas então a razão
entre dois segmentos quaisquer de uma delas é igual a razão entre segmentos
correspondentes da outra.
Ou seja:
AB
A' B'
BC
B'C '
AB
A' B'
=
ou
=
ou
=
e etc.
BC
B' C '
CD
C ' D'
AC
A' C '
Exemplo: Determine o valor de x na figura, sabendo que as retas são paralelas cortadas
por duas transversais.
1º solução.
15 x
=
⇒ 5 x = 15.4 ⇒ 5 x = 60 ⇒ x = 12
5 4
2º solução.
20 x + 4
=
⇒ 5( x + 4) = 20.4 ⇒ 5 x + 20 = 80 ⇒ 5 x = 80 − 20 ⇒ 5 x = 60 ⇒ x = 12
5
4
3º solução.
20 x + 4
⇒ 15( x + 4) = 20.x ⇒ 15 x + 60 = 20 x ⇒ 60 = 20 x − 15 x ⇒ 5 x = 60 ⇒ x = 12
=
15
x
ou simplesmente, uma quarta solução, observa-se que pela proporcionalidade entre os
segmentos, que o segmento maior da primeira transversal é 3 vezes maior que o
segmento menor. Logo o x também deve ser 3 vezes maior que o 4, logo o valor de x é 12.
Retornando a Física
Relação entre as escalas termométricas.
Para determinar a relação existente entre as escalas termométricas podemos
utilizar o que acabamos de aprender. O teorema de Tales é uma poderosa ferramenta
para determinar a proporcionalidade entre segmentos, que é exatamente o que buscamos
quando tentamos estabelecer uma relação entre as escalas.
Utilizando o teorema de Tales, podemos estabelecer a proporção entre os segmentos a e
b, em cada termômetro representado na figura.
Então temos:
a
C −0
F − 32
K − 273
=
=
=
⇒
b 100 − 0 212 − 32 373 − 273
Simplificando teríamos:
C
F − 32 K − 273
=
=
100
180
100
C F − 32 K − 273
=
=
5
9
5
RELAÇÃO ENTRE OUTRAS ESCALAS
As escalas termométricas não se resumem as três escalas estudadas
anteriormente, a maior atenção dada ao estudo delas é devido ao fato dessas escalas
serem padronizadas. Já foi dito que qualquer pessoa pode criar uma escala de sua
conveniência. para isso usaremos os passos vistos anteriormente para a criação de uma
escala termométrica e a relação de proporcionalidade do teorema de Tales.
Exemplo: O professor Willis resolveu criar uma escala termométrica que leve seu nome,
para isso adotou para temperatura do gelo – 40 e para o vapor 560. Determinar a fórmula
de conversão da escala Willis para a escala Celsius.
Então temos:
a
C −0
W − (−40)
=
=
b 100 − 0 560 − (−40)
⇒
C
W + 40
=
100 560 + 40
⇒
W + 40
6
Esta, portanto é a relação entre as escalas Celsius e a escala Willis.
simplificando: C =
C
W + 40
=
100
600
LISTA DE EXERCÍCIOS
TERMOMETRIA
1ªQuestão
(PUC/Campinas-SP) Sobre o conceito de calor pode-se afirmar que se trata de uma:
a) medida da temperatura do sistema.
b) forma de energia em trânsito.
c) substância fluida.
d) quantidade relacionada com o atrito.
e) energia que os corpos possuem.
2ªQuestão
(AFA-SP) Assinale a alternativa que define corretamente calor.
a) Trata-se de um sinônimo de temperatura em um sistema.
b) É uma forma de energia contida nos sistemas.
c) É uma energia em trânsito, de um sistema a outro, devido à diferença de temperatura entre eles.
d) É uma forma de energia superabundante nos corpos quentes.
e) É uma forma de energia em trânsito do corpo mais frio para o corpo mais quente.
3ªQuestão
(Unisa-SP) O fato de o calor passar de um corpo para outro deve-se a:
a) quantidade de calor existente em cada um.
b) diferença de temperatura entre eles.
c) energia cinética total de suas moléculas.
d) o número de colorias existente em cada um.
e) nada do que se afirmou acima é verdadeiro.
4ªQuestão
(FEI-SP) Quando dois corpos de tamanhos diferentes estão em contato e em equilíbrio térmico,
isolados do meio ambiente:
a) o corpo maior é o mais quente.
d) o maior cede calor para o menor.
b) o corpo menor é o mais quente.
e) o menor cede calor para o maior.
c) não há troca de calor entre eles.
5ªQuestão
Assinale a frase mais correta conceitualmente.
a) “Estou com calor”.
b) “Vou medir a febre dele”.
c) “O dia está quente; estou recebendo muito calor”.
d) “O dia está frio; estou recebendo muito frio”.
e) As alternativas c e d estão corretas.
6ªQuestão
Quando dois corpo de materiais diferentes estão em equilíbrios térmicos, isolados do meio ambiente,
pode-se afirmar que:
a) o mais quente é o que possui menor massa.
b) apesar do contato, suas temperaturas não variam.
c) o mais quente fornece calor ao mais frio.
d) o mais frio fornece calor ao mais quente.
e) suas temperaturas dependem de suas densidades.
7ªQuestão
Quando dois corpos de tamanhos diferentes estão em contato em equilíbrio térmico, isolados do
meio ambiente:
a)o corpo maior é o mais quente. d)o maior cede calor para o menor.
b)o corpo menor é o mais quente. e)o menor cede calor para o maior.
c)não há troca de calor entre eles.
8ªQuestão
Três corpos encostados entre si estão em equilíbrio térmico. Nessa situação:
a) os três corpos apresentam-se no mesmo estado físico.
b) A temperatura dos três corpos é a mesma.
c) O calor contido em cada um deles é o mesmo.
d) O corpo de maior massa tem mais calor que os outros dois.
9ªQuestão
Dois termômetros, um graduado na escala Celsius e o outro na escala Fahrenheit, fornecem a mesma
leitura para a temperatura de um gás. Determine o valor dessa temperatura.
10ªQuestão
Uma temperatura na escala Fahrenheit, é indicada por um número duplo daquele em que é
representada na escala Celsius. Esta temperatura é:
a)160°C
b) 148°C
c)140°C
d)130°C
e)120° C
11ªQuestão
Quando um corpo está numa temperatura que, em graus Celsius, tem a metade do valor medido em
Fahrenheit, pode-se afirmar que sua a temperatura é:
a)200°F
b)300°F
c)240°F
d)320°F
e) 160°F
12ªQuestão
A figura representa a correspondência entre as escalas de dois termômetros X e Y. Ambos as escalas
são lineares. Qual o valor na escala Y que corresponde 80°X na escala X?
X
80°X
Y
?
20°X
60°Y
0°X
20°Y
a) 80°C
b) 100°C
d) 180°C
e)220°C
c) 120°C
13ªQuestão
Duas escalas termométricas lineares estão representadas na figura. Uma °X outra em °Y. Onde a
escala X marca 100°X, a escala Y marca 80°Y e onde a escala X marca 0°X, a escala Y marca 20°Y.
Quando a escala X marcar 50°X, quantos °Y marcara a escala .
14ªQuestão
Na temperatura do gelo fundente, um termômetro marca 0,3°C e na ebulição da água pura, sob
pressão atmosférica normal, 100,2°C. Logo, a leitura termométrica, nesse instrumento, que não
requer correção é:
a) 2°C
b) 100°C
c) 6°C
d)3°C
e) 60°C
15ªQuestão
(Fatec-SP) A televisão noticia que a temperatura em Nova York chegou aos 104 graus (naturalmente
104 graus Fahrenheit). Converta para graus Celsius.
16ªQuestão
Certa escala termométrica adota os valores –20 e 580, respectivamente, para os pontos do gelo e do
vapor. Determine:
a) a fórmula de conversão entre essa escala e a escala Celsius.
b) A indicação que nessa escala corresponde a 20°C.
DILATAÇÃO DOS SÓLIDOS
Quando aquecemos um corpo, ou seja, aumentamos sua temperatura,
geralmente suas dimensões também aumentam. Esse aumento se dá devido a maior
agitação das moléculas do corpo. Ao contrario quando diminuímos a temperatura de um
corpo, suas dimensões diminuem, devido a menor agitação molecular.
A agitação molecular, causa da dilatação dos corpos, se dá em todas as
direções, por esse motivo toda dilatação é volumétrica, porém em alguns casos pode-se
desprezar uma ou duas direções dessa dilatação, pois algumas dilatações tornam-se
desprezíveis em relação a outras.
Quando se analisa a dilatação em uma só direção, o comprimento de uma
barra de ferro, por exemplo, estaremos estudando a DILATAÇÃO LINEAR. Quando se
analisa a dilatação em duas direções, a superfície de uma chapa de aço, por exemplo,
estaremos estudando a DILATAÇÃO SUPERFICIAL. Quando se analisa a dilatação em
todas as direções, estaremos estudando a DILATAÇÃO VOLUMETRICA.
DILATAÇÃO LINEAR
Suponhamos que você aqueça uma barra de metal. A variação do comprimento
dessa barra (∆L ) depende de três fatores, o comprimento inicial da barra (L0), o material
de que ela é feita, para esse fator temos o que chamamos de coeficiente de dilatação
linear ( α ), e a variação de temperatura (∆T ) . Logo podemos escrever a seguinte equação:
∆L = L0α ∆T
∆L = L – L0
L0
L
α
∆T = T – T
Variação de comprimento
→
→
Comprimento Inicial
→
Comprimento Final
→
Coeficiente de Dilatação Linear
→
Variação de Temperatura
Logo, temos que:
L = L0 + ∆L
Substituindo ∆L por
L0α ∆T
Ficamos com:
L=L0 + L0α ∆T
Colocando L0 em evidência
L = L0( 1 – α ∆T )
Revisando Matemática – Potências e suas propriedades.
Potência é uma ferramenta muito utilizada nas ciências para representar números muito
grandes ou muito pequenos.
Definição:
Para n inteiro maior que zero, temos:
a n = a1
.a.a4
...
42
3a
n vezes
Ou seja: Um número a (base) elevado a n (expoente) é dado pela base multiplicada por ela
mesma o número de vezes do expoente.
Exemplos:
3 4 = 31
.32
.33
.3 = 81
4 vezes
5 3 = 5{
.5.5 = 125
3vezes
Propriedades:
1º) Em um produto de potencias de mesma base é igual à potencia que se obtém
repetindo a base e somando os expoentes.
a m .a n = a m + n
Exemplos:
34.37 = 34 + 7 = 311
53.56 = 53 + 6 = 59
2º) Em um quociente de potencias de mesma base é igual à potencia que se obtém
repetindo a base e subtraindo os expoentes.
am : an = am−n
Exemplos:
36 : 32 = 36 − 2 = 34
715.713 = 715 −13 = 7 2
3º) Em uma potencia de outra potencia é igual à potencia que se obtém repetindo a base e
multiplicando os expoentes.
(a )
m n
= a m. n
Exemplos:
(5 )
(2 )
3 6
= 53.6 = 518
3 5
= 23.5 = 215
4º) Em uma potencia de um produto é igual ao produto das potencias formadas pelos
fatores do produto com o expoente do produto.
(a.b )m = a m .b m
Exemplos:
(3.5)2 = 32.52
(2.7 )9 = 29.79
Potência de base 10.
Podemos ainda ter potencias cuja base é 10. Nesses casos a potência será representada pelo
número 1 seguido pela quantidade de zeros tal qual seja o número presente no expoente.
Exemplos:
10 3 = 1000
{
3 zeros
10 7 = 10000000
1
424
3
7 zeros
Potência com expoente negativo
a−n =
1
(para a ≠ 0 )
an
Exemplos:
3−5 =
1
35
8− 7 =
1
87
1
= 325
−5
32
1
= 2.103
−3
2.10
Ou seja, para deslocar uma potência do denominador para o numerador ou vice versa, basta
trocar o sinal do expoente.
Notação Científica.
Em ciências nos deparamos com alguns números que são muito grandes ou
muito pequenos. Estes números, geralmente, possuem um número muito grande de zeros.
Para tornar a escrita desses números mais simples, existe uma forma que chamamos de
notação cientifica que consiste em escrever esse número em duas partes, a primeira n ,
chamada de coeficiente e a segunda uma potência de 10.
g = n.10 x
onde:
1 ≤ n < 10
e
x ∈ Z (INTEIROS)
Exemplos:
350000000 = 3,5.108
0,00000125 = 1,25 x10−6
Note que ao termos um número escrito na forma de notação cientifica, este se
torna mais agradável aos olhos e as operações com eles tornam-se mais simples.
Método prático para escrever um número em notação científica.
1º Caso: Para números muito grandes
1º passo: Reescrevemos o número colocando a vírgula imediatamente a direita do
primeiro algarismo.
2º passo: Contamos quantos são os algarismos à direita da vírgula. Esta
quantidade será o expoente da potência de base 10 que aparecerá na notação
científica.
3º passo: Escrevemos então os algarismos iniciais do número com a vírgula, sem
os “zeros” que estiverem a direita do último número. Acrescentando em seguida a
potência de dez, encontrada no 2º passo.
Exemplos:
1º) 27100000
7
2, 7100000
1
424
3 = 2,71x10
7 a lg arismos
2º) 4359000000000000
15
4, 3590000000
144
42400000
44
3 = 4,359 x10
15 a lg arismos
2º Caso: Para números muito pequenos.
1º passo: Reescrevemos o número
imediatamente a direita do
primeiro algarismo diferente de zero.
colocando
uma
segunda
vírgula
2º passo: Contamos quantos são os algarismos entre as vírgulas. Esta quantidade
será o expoente da potência de base 10 que aparecerá na notação científica, com
o sinal negativo.
3º passo: Escrevemos então os algarismos a partir do primeiro, com a vírgula, sem
os “zeros” que estiverem a esquerda do primeiro número. Acrescentando em
seguida a potência de dez, encontrada no 2º passo.
Exemplos:
1º) 0,00000000128
−9
0, 000000001
14243,28 = 1,28 x10
9 a lg arismos
2º) 0,00000000000000097456
−16
0, 0000000000
144424000009
443,7456 = 9,7456 x10
16 a lg arismos
Como foi dito no 2º passo, o expoente da potência de 10 é exatamente o número de casas
que deslocamos a vírgula, com sinal negativo.
Operações com números na forma de notação científica.
Introdução:
Podem existir números que estão escritos na forma de potência de 10, mas não
necessariamente na forma de notação científica. Vimos que em um número na forma de
notação científica deve ter o módulo do seu coeficiente variando entre 1 e 10, sendo assim, o
número 7000x105 está escrito em uma base 10, mas não na forma de notação científica.
Como podemos então, transformar esse número em uma notação científica.
Sabemos que 7000 = 7 x103 então 7000 x105 = 7 x103 x105 , pela propriedade de potência temos
que 7 x103 x105 = 7 x103 + 5 = 7 x108 , logo podemos concluir que 7000 x105 = 7 x108 .
Percebam que é um processo longo de transformação, por esse motivo temos um método
bem eficaz para fazer esses tipos de transformações.
Forma prática:
Quando é necessário que a vírgula se desloque y casas para a esquerda: somase no expoente da base 10 o valor y.
Quando é necessário que a vírgula se desloque y casas para a direita: subtrai-se
no expoente da base 10 o valor y.
Exemplos:
1º) 53642x107
Temos que levar a vírgula para frente do algarismo 3, logo vamos deslocá-la 4 casas para a
esquerda, então devemos somar 4 unidades ao expoente da base 10.
53642 x107 = 5,3642 x107 + 4 = 5,3642 x1011
2º) 0,0000035 x109
Temos que levar a vírgula para frente do algarismo 5, logo vamos deslocá-la 6 casas para a
direita, então devemos subtrair 6 unidades ao expoente da base 10.
0,0000035 x10 9 = 3,5 x10 9−6 = 3,5 x10 3
Adição e subtração
Para somar ou subtrair números na forma de notação científica, não podemos fazer essa
operação diretamente, precisamos tomar alguns cuidados e seguir alguns passos:
1º) Igualamos os expoentes das potências;
2º) Coloca-se em evidência a potência, que agora, é comum as parcelas;
3º) Soma-se ou subtrai-se os coeficientes das parcelas;
4º) Se necessário coloca-se o resultado como notação científica.
Exemplo
Dados os números A = 3,45x107, B = 9,5x105 e C = 4,25x103, determine:
a) A + B =
A + B = 3,45 x107 + 9,5 x105 = 345 x105 + 9,5 x105 = (345 + 9,5) x105 = 354,5 x105 = 3,545 x107
b) B + C =
B + C = 9,5 x105 + 4,25 x103 = 950 x103 + 4,25 x103 = (950 + 4,25) x103 = 954,25 x103 = 9,5425 x105
Multiplicação e divisão
Para multiplicar ou dividir números em notação científica, basta multiplicar ou dividir os
coeficientes e utilizar a propriedade de potencia para as potencias de mesma base 10.
Podemos utilizar os seguintes passos:
1º) Separamos os coeficientes das potencias de base 10.
2º) Multiplica-se ou divide-se os coeficientes.
3º) Aplica-se as propriedades de potências as potências de base 10, ou seja, somar os
expoentes, se a operação for de multiplicação, ou subtrair os expoentes se a operação for de
divisão.
4º) Se necessário coloca-se o resultado como notação científica.
Exemplo:
Dados os números A = 3,45x107, B = 9,5x105 e C = 4,25x103, determine:
a) A x B =
AxB = 3,45 x107 x9,5 x105 = 3,45 x9,5 x107 x105 = 32,775 x107 + 5 = 32,775 x1012 = 3,2775 x1013
b) B : C =
B : C = 9,5 x105 : 4,25 x103 = (9,5 : 4,25) x(105 : 103 ) ≅ 2,235 x105 −3 = 2,235 x102
Retornando a Física
Exercícios resolvidos.
1) Uma barra apresenta a 20 ºC um comprimento de 50 m, sendo feita de um material cujo
coeficiente de dilatação linear vale 1,6. 10-5 ºC-1. A barra é aquecida até 120 ºC. Determine
o comprimento da barra ao final do aquecimento.
Solução:
∆L = L0 .α .∆t
∆L = 5000.x1,6 x10− 5 x100
 Lo = 50m = 5000cm

−5
α = 1,6 x10
∆t = 120 − 20 = 100º C

∆L = 5 x103 x1,6 x10− 5 x102
∆L = (5 x1,6) x(103 x10 −5 x10 2 )
∆L = 8 x103 −5 + 2
L = 5000 + 8 = 5008 cm
∆L = 8 x100
∆L = 8 x1
∆L = 8 cm
EXERCÍCIOS
1ª Questão
Uma barra apresenta a 20°C comprimento de 50 metros sendo feita de um material cujo coeficiente de
dilatação linear médio vale 15.10-6. A barra é aquecida até 70°C. Determine a dilataçao ocorrida e o
comprimento final da barra.
2ªQuestão
Uma barra de cobre tem um comprimento de 20m, a uma temperatura de 30°C. Sabendo-se que a barra foi
aquecida até 50°C e o coeficiente de dilatação linear do cobre é de 1,6.10-5 °C-1, determine a dilatação
ocorrida e o comprimento final da barra.
3ª Questão
Uma barra de metal apresenta um comprimento de 30 metros sendo feita de um material cujo coeficiente
de dilatação linear médio vale 2.10-5. Qual deve ser a variação da temperatura para que essa barra alcance
30,03 metros?
Óptica
Princípios Básicos da Propagação da Luz
DEFINIÇÕES E CONCEITOS
1ª-Luz
É o agente físico responsável pelas sensações visuais.
2ª-Fonte de Luz
É todo corpo que emite luz. Ela pode ser primária ou secundária.
Fonte de Luz Primária (Fonte Luminosa)
É aquela que emite luz própria.
Ex:. Sol, lâmpada, vela, etc.
Fonte de Luz Secundária (Fonte Iluminada)
É aquela que emite a luz que recebe de outros corpos.
Ex:.a Lua.
Fonte de Luz Puntiforme ou Pontual
É toda fonte cujas dimensões são consideradas desprezíveis em relação ás distâncias envolvidas.
•
Fonte de Luz Extensa
É toda fonte cujas dimensões não podem ser desprezadas em relação às distâncias envolvidas.
3ª-Raio de Luz
É toda linha que representa geometricamente a propagação da luz.
4ª-Feixe de Luz
É o conjunto de raios de luz. Um feixe de luz pode ser:
Paralelo
Convergente
Divergente
5ª-Meio Isótropo
É aquele que apresenta as mesma propriedades em todas sua extensão, independe da direção avaliada.
6ª-Luz Monocromática(Luz Simples)
É aquela que apresenta uma só freqüência. Em óptica, luz monocromática é a luz de uma só cor.
7ªLuz Policromática ( Luz Composta)
É aquela que apresenta mais de uma freqüência.
Ex:. luz do sol (luz branca).
Obs:.A composição da luz branca vinda do Sol pode ser observada quando ocorre o arco-íris.
MEIOS DE PROPAGAÇÃO
1Meio Transparente: É aquele que permite a propagação da luz através
de si. Em seu interior a luz não perde o paralelismo (no caso de incidência de feixe de
luz paralela sobre este meio). A visualização deste objeto através deste meio, possui
total nitidez
Feixe de luz
Incidente
2-Meio Translúcido: É aquele que permite a propagação da luz através de si, mas o
feixe perde se paralelismo, e assim o objeto visto através dele, perde a sua nitidez.
Luz Incidente
Perda de paralelismo
3-Meio Opaco: È aquele que impede a propagação da luz através de si, não permitindo
a visualização dos objetos através deles.
Feixe Incidente
VELOCIDADE DA LUZ
A Luz se propaga tanto no espaço como no vácuo. Para que haja propagação da luz, não
há necessidade de meio material
A velocidade da luz no ar e no vácuo tem medidas experimentalmente e apresentaram
os seguintes valores:
Cvácuo = 299.793,0 km/s
CAr = 299.700,0 km/s
Podemos admitir que a velocidade da luz tanto no ar como no vácuo é da ordem de 300.000km/s ou
3.108m/s
FENÔMENOS LUMINOSOS
Reflexão: A luz propaga-se pelo meio A, atinge a superfície S e volta para o meio A do qual é
proveniente.
Feixe Incidente
(A)
Feixe Refletido
(S)
Reflexão Irregular ou Difusa
O feixe incidente é paralelo, mas o feixe refletido perde o paralelismo espalhando-se em varias
direções.
(A)
(S)
OBS:. A reflexão difusa é responsável pela visão dos corpos que nos rodeiam
REFRAÇÃO
O Feixe de luz propagando-se pelo meio A atinge a superfície S e passa para o meio B.
(A)
(S)
(B)
ABSORÇÃO
O feixe de luz propagando-se no meio A atinge a superfície S e não retorna ao meio A;
Nem passa para o meio B, isto é, ele é absorvido provocando aquecimento da superfície S.
A COR DE UM CORPO
O Sol emite a luz branca que é formada por várias luzes monocromáticas. A cor de um
corpo iluminado pela luz branca é determinada pela seletividade com que ele absorve a
reflete difusamente a luz incidente.
Se um corpo iluminado com a luz branca reflete a cor azul e absorve as demais, ele
terá cor azul. Se ele absorver todas, terá cor preta, se não absorver nenhuma, terá cor
branca.
Portanto a cor de um corpo depende da luz incidente e é determinada pela luz que ele
reflete difusamente.
PRINCÍPIOS DA ÓPTICA GEOMÉTRICA
A óptica geométrica é baseada em três princípios conhecidos como princípios
fundamentais da óptica geométrica.
1ª PRINCÍPIO DA PROPAGAÇÃO RETILÍNEA DO RAIO DE LUZ:
A luz se propaga em linha reta num meio homogêneo, transparente e isótropo.
2ª PRINCÍPIO DA INDEPENDÊCIA DOS RAIOS DE LUZ:
Os raios de luz de um feixe são independente, se um raio luminoso cortar outro, ele
continua seu caminho sem interferência.
3ª PRINCÍPIO DA REVERSIBILIDADE DOS RAIOS DE LUZ:
Quando permutamos as posições da fonte de luz e do observador, o caminho de um raio
de luz não se altera.
FENÔMENOS QUE OCORREM COM BASE NO PRINCÍPIO DA
PROPAGAÇÃO RETILÍNEA DA LUZ
SOMBRA E PENUMBRA
Formação de Sombra por fonte Puntiforme(pontual)
(Total ausência de luz)
sombra
fonte puntiforme
anteparo opaco
A formação de uma Penumbra por uma Fonte Extensa
A região de penumbra é iluminada parcialmente pela fonte
fonte extensa
anteparo opaco
penumbra
sombra
penumbra
Revisando Matemática (Geometria).
Ângulos
Ângulo é a reunião de duas semi-retas de mesma origem.
O Ângulo acima representado é o ângulo AÔB, de vértice O e lados OA e OB.
Um ângulo é medido em graus, representado pelo símbolo ° após o número.
1 grau é igual a 1/360 da circunferência, logo uma circunferência tem 360°.
Ângulos congruentes
São ângulos que possuem a mesma medida.
Tipos de ângulos
1º) Ângulo nulo – sua medida é de 0°
2º) Ângulo agudo – sua medida é menor que 90°
3°) Ângulo reto – sua medida é de 90º
4°) Ângulo obtuso – sua medida é maior que 90°
5º) Ângulo raso ou de meia volta – sua medida é de 180°
6º) Ângulo de uma volta – sua medida é de 360º
7º) Ângulos complementares – São dois ângulos cujas medidas somam 90º.
8º) Ângulos suplementares – São dois ângulos cujas medidas somam 180º.
7º) Ângulos replementares – São dois ângulos cujas medidas somam 360º.
Bissetriz de um ângulo
Bissetriz é a semi-reta interna ao ângulo, que o divide em dois ângulo de
mesma medida (congruentes).
Exemplos:
1) Um ângulo mede 30°, determine a medida de seu complemento, seu suplemento e
seu replemento.
Complemento = 60°
Suplemento = 150°
Replemento = 330°
2) Um ângulo CÔD mede 80°, sabendo que OF é bissetriz desse ângulo. Determine a
medida de FÔD.
A Medida de FÔD é metade da medida de CÔD, logo 40°.
Triângulos
Definição
É um polígono de três lados.
Elementos
Lados: AB, BC e CA.
Vértices: A, B e C.
Ângulos internos: Â , B̂ e Ĉ
Classificação
Podemos classificar os triângulos de duas formas:
Quanto aos lados:
Eqüilátero: 3 lados de mesma medida
Isósceles: 2 lados de mesma medida
Escaleno: 3 lados de medidas diferentes
Quanto aos ângulos:
Acutângulo: Possui 3 ângulos agudos, ou seja, medindo menos de 90°
Retângulo: Possui um ângulo reto, ou seja, medindo 90°
Obtusângulo: Possui um ângulo obtuso, ou seja, medindo mais de 90°
Soma dos ângulos internos de um triângulo
Em um triângulo os ângulos internos são suplementares, ou seja, sua soma é de 180°.
Exemplo:
Semelhança de triângulos
Observe os triângulos ABC e DEF, abaixo:
Podemos notar que os dois triângulos têm a mesma forma e que por consequência os
ângulos correspondentes são congruentes.
Notamos também que se calcularmos as razões entre os lados correspondentes,
encontramos:
AB
4 1
=
=
12 3
DE
BC
3 1
=
=
9 3
EF
CA
2 1
=
=
FD 16 3
Então, as razões são iguais, ou seja, os lados dos triângulos são proporcionais. Essa
razão encontrada é chamada de razão de semelhança.
AB BC
CA
1
=
=
=
3
DE EF
FD
Podemos notar claramente que os lados de DEF são três vezes maiores que seus
correspondentes em ABC, logo diremos que ABC e DEF são semelhantes.
Logo, triângulos semelhantes são aqueles que têm ângulos correspondentes congruentes
e os lados correspondentes proporcionais.
Exemplos:
1) Determine os valores de a e b sabendo que os triângulos são semelhantes:
Note que a razão de semelhança do menor para o maior é de 1 para 3, ou seja, o
triângulo HIJ é três vezes maior que DEF, então cada lado de HIJ deve ser três
vezes maior que seu correspondente em DEF.
Então, a = 42 cm e b = 21 cm.
2) Os lados de um triângulo medem 20 cm, 25 cm e 30 cm. Determine os lados de um
triangulo que seja menor que o anterior, sabendo que a razão de semelhança é de 1
para 5.
Como a razão de semelhança é de 1 para 5, temos que o triangulo menor, que é o
procurado, é cinco vezes menor do que o dado no exercício, logo as medidas do
triangulo menor devem ser 4 cm, 5 cm e 6 cm.
CAMARA ESCURA DE ORIFÍCIO
É toda caixa de paredes opacas, na qual uma delas possui um pequeno orifício por onde
penetram os raios de luz provenientes de uma fonte. Esses raios atravessam o orifício e
atinge a parede oposta formando uma imagem invertida.
i
o
x
o
i
y
= x
y
Onde :
o
i
x
y
tamanho do objeto
tamanho da imagem
distancia do objeto a câmara
comprimento da câmara
EXEMPLO
1ªQuestão
Uma câmara escura de orifício tem comprimento de 40cm. De um poste de 8m de altura
obtêm-se, na parede oposta, uma imagem de 5cm de altura. Determine a distância entre
a câmara e o poste.
o
i
x
y
EXERCÍCIOS
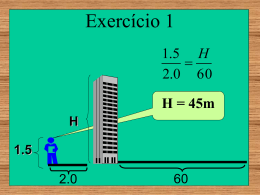
1ªQuestão
Um muro de 2m de altura produz uma sombra de 60cm. No mesmo instante, um prédio produz uma
sombra de 15m. Determine a altura do prédio.
H
2m
15m
60cm
2ªQuestão
Uma câmara escura de orifício apresenta comprimento de 60cm. De uma árvore de altura 6m obtevese, no anteparo fosco, uma imagem de altura 30cm. Determine a distância da árvore até à câmara.
3ªQuestão
Uma fonte luminosa projeta luz sobre as paredes de uma sala;
Um pilar intercepta parte desta luz. A penumbra que se observa é devida:
(a)ao fato de não ser pontual a fonte luminosa
(b)ao fato de não ser propagar a luz rigorosamente em linha reta
(c)aos fenômenos de interferência da luz depois de tangenciar os bordos do pilar
(d)aos fenômenos de difração
(e)à incapacidade do globo ocular em concorrer para uma diferenciação eficiente da linha divisória
entre luz e penumbra.
4ªQuestão
Um espelho plano se afasta de um objeto parado em relação à Terra com velocidade de translação de
10m/s. Determine a velocidade da imagem em relação:
(a) ao espelho
(b)ao observador
5ªQuestão
Determine os ângulos pedidos nos sistemas abaixo
6ªQuestão
No esquema da figura representamos o Sol, a Terra e a Lua. Para um observador na superfície da Terra
voltada para a Lua
Ponto O
Cone de sombra
a
LUA
SOL
TERRA
a) é noite, fase de Lua Nova e ocorre eclipse da Lua.
b) é dia, fase de Lua Cheia, e ocorre eclipse do Sol.
c) é noite, fase de Lua Cheia e a Lua está visível.
d) é dia, fase de Lua Nova e ocorre eclipse da Lua.
e) é noite, fase de Lua Cheia, e ocorre eclipse da Lua.
7ªQuestão
Um muro de 2m de altura produz uma sombra de 60cm. No mesmo instante, um prédio produz uma
sombra de 15m. Determine a altura do prédio.
H
2m
15m
60cm
8ªQuestão
Uma câmara escura de orifício apresenta comprimento de 60cm. De uma pilastra de 6m obteve-se, no
anteparo fosco, uma imagem de altura 30cm. Determine a distância da pilastra até à câmara.
9ªQuestão
Uma fonte luminosa projeta luz sobre as paredes de uma sala;
Um pilar intercepta parte desta luz. A penumbra que se observa é devida:
(a)ao fato de não ser pontual a fonte luminosa
(b)ao fato de não ser propagar a luz rigorosamente em linha reta
(c)aos fenômenos de interferência da luz depois de tangenciar os bordos do pilar
(d)aos fenômenos de difração
(e)à incapacidade do globo ocular em concorrer para uma diferenciação eficiente da linha divisória
entre luz e penumbra.
10ªQuestão
Um espelho plano se afasta de um objeto parado em relação à Terra com velocidade de translação de
10m/s. Determine a velocidade da imagem em relação:
(a) ao espelho
(b)ao observador
11ªQuestão
Determine os ângulos pedidos nos sistemas abaixo
12ªQuestão
Um pedaço de tecido vermelho, quando observado numa sala iluminada com luz azul parece:
a)preto.
b)branco.
c)vermelho.
d)azul.
e) amarelo.
13ªQuestão
Um objeto que se apresenta amarelo quando exposto à luz solar é colocado em um quarto escuro.
Qual será a cor deste objeto , se acendermos no quarto uma luz monocromática azul ?
a)azul.
b) amarela.
c)branca.
d)vermelha.
e)preta
14ªQuestão
Um raio luminoso reflete-se em um espelho plano. O ângulo entre os raios incidentes e refletido mede
35,0º. O ângulo de incidência mede:
a)20,5º
b )17,5º
c)35º
d) 70º
e)85º
15ªQuestão
Um espelho plano fornece de um objeto real, uma imagem;
a)real. B)que pode ser projetada num anteparo. c)no foco do espelho d)virtual.
e)situada a uma distância maior que a distância do objeto ao mesmo.
16ªQuestão
Um pincel de raios paralelos quando refletido por um espelho plano:
a)conserva-se paralelismo b)diverge c)é difundido
d)converge
e)n.r.a.
17ªQuestão
Um espelho plano vertical conjuga a imagem de um vaso situado a 3,5m de distância. Afasta-se o
.espelho, de 2m, mantendo-o ainda vertical, que distância passa a separar as duas imagens (inicial e
final).
18ªQuestão
Um motorista que está a 60km/h , vê pelo espelho plano retrovisor de seu carro, a imagem de uma
casinha que está à beira da estrada. Determine:
a)a velocidade da imagem em relação à estrada,
b)a velocidade da imagem em relação ao motorista.
19ªQuestão
Um eclipse solar só pode ocorrer quando:
a)é fase de lua nova.
d)é fase de lua em quarto minguante.
b)é fase de lua cheia.
e)n.r.c.
c)é fase de lua em quarto crescente.
20ªQuestão
Um jogador de basquete de 2,10m de altura olha-se num espelho plano e vertical, colocado no
vestiário, e visualiza inteiramente a sua imagem, independente da distância dele ao espelho. Determine
a altura mínima do espelho.
21ªQuestão
Um raio de luz incide perpendicularmente sobre uma superfície refletora. Qual é o valor do ângulo de
incidência
22ªQuestão
Uma câmara de orifício apresenta comprimento de 100cm. Determine a tamanho da imagem formada
no seu interior, de um objeto de comprimento 50cm colocado a 10m de distancia da mesma.
x
y
23ªQuestão
Dois raios de luz se propagam um meio transparente e homogêneo, interceptando-se num ponto P.
Após a intersecção, os raios:
(a)continuam sobre as mesmas retas que os continham antes da intersecção
(b)desaparecem
(c)passam a se propagar, segundo linhas curvas
(d)continuam a se propagar em linhas retas, mas desviados, em relação àquela que os continham
antes da intersecção
24ªQuestão
Um motorista, viajando a 50km/h, observa no espelho plano retrovisor a imagem de um poste na
estrada. Qual a velocidade dessa imagem:
(a)em relação à estrada
(b)em relação ao motorista
25ªQuestão
Determine os ângulos pedidos nos sistemas abaixo
27ªQuestão
Um observador nota que um edifício projeta no solo uma sombra de 60m de comprimento no instante
em que uma haste vertical de 80cm de altura projeta no solo uma sombra de comprimento 0,20m.
Determine a altura do edifício H
S
s
A COR DE UM CORPO
A luz branca emitida pólo Sol é composta por varias luzes monocromáticas. As sete principais são:
Vermelha, Laranja, Amarelo, Verde, Azul, Anil e Violeta. Cada qual com sua freqüência bem
definida, que vai de 1014Hz para o vermelho até 1015Hz.
Um corpo iluminado pela cor branca terá sua cor determinada pela seletividade com que ele absorve e
reflete difusamente a luz que incide sobre si. Por exemplo podemos dizer que um corpo que é
iluminado com a cor branca e se apresenta com a cor vermelha significa que este corpo refletiu
difusamente a cor vermelha e absorveu as demais.
LUZ BRANCA INCIDENTE
vernelho
LUZ VERMELHA REFLETIDA DIFUSAMENTE
OBS:. Um corpo que se apresenta com a cor preta ao ser iluminado com luz branca,
significa que este corpo absorveu todas a cores e não refletiu nenhuma. Porém se um corpo
for iluminado com a cor branca e se apresentar na cor branca, significa que este corpo
refletiu todas as cores sem absorveu nenhuma.
ESPELHOS
DEFINIÇÃO: Superfície polida com grande capacidade de reflexão de luz. Possui a
propriedade de formação de imagens através de reflexão regular.
Tipo de espelhos:
1º Espelhos Planos: Este tipo de espelho é formado por uma superfície plana, polida
e com grande capacidade de formar imagens atrever de reflexão regular.
RAIO DE LUZ
INCIDENTE
RAIO DE LUZ
REFLETIDO
ESPELHO PLANO
2º Espelhos Esféricos: Este tipo de espelho é formado por uma superfície esférica,
polida e com grande capacidade de formar imagens atrever de reflexão regular.
SUPERFÍCIE REFLETORA
RAIO INCIDENTE
RAIO REFLETIDO
REFLETIDO
SUPERFÍCIE REFLETORA
RAIO INCIDENTE
RAIO
OBS:. Verificamos que os espelhos esféricos se apresentam de duas formas bem definidas :
O 1º é chamado côncavo, pois possui a superfície interna refletora
O 2º é chamado convexo, pois apresenta a superfície externa refletora
LEI DA REFLEXÃO REGULAR
Considere inicialmente I um raio de luz que incide sobre uma superfície S plana espelhada
como indica a figura abaixo.
N
I
R
S
Neste caso podemos observar alguns elementos fundamentais da reflexão:
I
Raio Incidente na Superfície S
R
Raio Refletido pela Superfície S
N
Superfície Normal Perpendicular (imaginária)
a Superfície S
iˆ
Ângulo de Incidência
r̂
Ângulo de Reflexão
1ª LEI DA REFLEXÃO REGULAR
Raio incidente I, o raio refletido R e a superfície normal N são coplanares, isto é, fazem
parte do mesmo plano.
2ª LEI DA REFLEXÃO REGULAR
O ângulo de incidência i e o ângulo de reflexão r são exatamente iguais: iˆ = rˆ
IMAGENS FORMADAS POR UM ESPELHO PLANO
IMAGEM DE UM PONTO MATERIAL FORMADA POR UM ESPELHO PLANO
O
●
I
●
X
X’
Características da imagem de um ponto material formada por um
espelho plano:
1ª- Imagem e objeto são eqüidistantes do espelho plano, ou seja X = X’
2ª- A imagem formada pelo espalho plano do ponto material é virtual
ou seja, formada atrais do espelho
IMAGEM DE CORPO EXTENSO FORMADA POR UM ESPELHO PLANO
B
B’
A
A’
C
C’
Obs:. Essa imagem também é virtual, pois é formada trás do espelho. Verificamos que ela
possui o mesmo tamanho do objeto, que é uma característica da imagem formada pelo
espelho plano.
IMAGEM DE CORPO EXTENSO FORMADA POR UM ESPELHO
ESFÉRICO
Para aprendermos a construir a imagem de um corpo extenso em um espelho esférico é
necessário que venhamos a conhecer as características da reflexão de três raios incidentes
em um espelho plano:
ELEMENTOS DE UM ESPELHO ESFÉRICO
v - vértice do espelho
C - centro de curvatura do espelho
F - fóco do espelho
OBS:. A linha que corta o espelho esférico passando pelo vértice, pelo foco e pelo centro de
curvatura do espelho é denominada eixo principal do espelho esférico.
1ª RAIO QUE INCIDE PARALELO AO EIXO PRINCIPAL DO ESPELHO: este raio é
refletido na direção do foco do espelho
RR
RI
RI
EIXO
V
PRINCIPAL
F
C
C
F
V
RR
2ª RAIO QUE INCIDE NO VERTICE DO ESPELHO: este raio é refletido com ângulo de
incidência igual ao ângulo de reflexão, em relação ao eixo principal
RI
RI
V
F
C
C
F
V
RR
RR
3ª RAIO QUE INCIDE NA DIREÇÃO DO FOCO DO ESPELHO: este raio é refletido
paralelamente ao eixo principal
RI
RR
RI
V
F
C
C
F
V
RR
4ª RAIO QUE INCIDE NA DIREÇÃO DO CENTRO DE CURVATURA DO ESPELHO:
este raio é refletido sobre si mesmo
RI
RR
RR
RI
V
F
C
C
F
V
OBS:. A formação de imagens nesses espelhos consiste no cruzamento de pelo menos dois
raios refletido, no caso do espelho côncavo, e do cruzamento do prolongamento de pelo
menos dois raios refletidos, no caso do espelho convexo.
CONSTRUÇÃO GEOMÉTRICA DE IMAGENS FORMADAS
POR ESPELHOS ESFÉRICOS
ESPELHO CONCAVO.
As imagens de um objeto formadas por um espelho esférico, depende da localização desse
objeto em relação ao espelho. Serão analisadas cinco posições do objeto em relação ao
espelho, ou seja, verificaremos as características das imagens, nas diferentes posições desse
objeto em relação ao espelho.
1ª Objeto situado depois do centro de curvatura
O
V
F
C
i
Características da imagem: Real (formada na frente do espelho), Menor (se comprimento
é menor que o comprimento do objeto) e invertida (a imagem fica de cabeça para abaixo
em relação ao objeto), localizada entre o foco e o centro de curvatura do espelho.
OBS:. Na localidade do objeto, se tivéssemos escolhido quaisquer outros raios, a imagens
seria a mesma.
2ª Objeto situado sobre o centro de curvatura do espalho
O
V
F
C
i
Características da imagem: Real, invertida e do mesmo tamanho do objeto, localizada
exatamente no centro de curvatura do objeto.
3ª Objeto situado entre o centro de curvatura e o foco do espelho
O
V
F
C
i
Características da imagem: Real, invertida e maior do que o objeto, localizada após o centro
de curvatura do objeto.
4ª Objeto situado sobre o foco do espelho
O
V
F
C
Características da imagem: Imprópria, os raios refletidos são paralelos
4ª Objeto situado entre o vértice e o foco do espelho
i
O
V
F
C
Características da imagem: Virtual, direita (mesma posição que o objeto) e maior do que o
objeto, localizada após o centro de curvatura do objeto.
ESPELHO CONCAVO.
No caso do espelho convexo o procedimento é basicamente o mesmo, porém só teremos
uma forma de imagem obtida pois qualquer que seja a posição que colocarmos o objeto só
teremos uma forma de imagem.
VERIFICAÇÃO
O
i
C
F
V
OBS:. Podemos observar que independente de onde colocarmos o objeto no eixo principal
do espelho convexo a imagem será sempre virtual, direita e menor que o objeto.
Foram escolhidos dois raios, um que vai na direção do foco e outro que vai paralelo ao eixo
principal.
EXERCÍCIOS
1ª Questão
(CESGRANRIO) Quando você se olha em um espelho côncavo e vê seu rosto aumentado,
seu rosto se encontra:
a)no foco do espelho.
b)no centro de curvatura do espelho.
c)entre o foco e o espelho.
d)entre o foco e o centro de curvatura.
e)mais afastado que o centro de curvatura, em relação ao espelho.
2ª Questão
(F. M. ABC) Com relação às imagens conjugadas a objetos reais por espelhos esféricos, é
correto afirmar que:
a)são sempre virtuais para um espelho côncavo.
b)são sempre reais para um espelho convexo.
c)são reais e invertidas quando o objeto é colocado sobre o foco de um espelho côncavo.
d)são sempre diretas e virtuais para um objeto colocado a uma distância ao espelho menor
que a distância ao focal.
e)reduzem-se a um ponto quando o objeto é colocado a uma distância ao espelho igual ao
raio de curvatura.
3ª Questão
(GAMA FILHO) A imagem formada em um espelho convexo de um objeto no finito,
colocado a uma distância finita, é:
a)virtual, direita e menor que o objeto.
b)virtual, invertida e menor que o objeto.
c)real, invertida e maior que o objeto.
d)real, direita e menor que o objeto.
e)real, direita e maior que o objeto.
4ª Questão
(F. Estácio de Sá-RJ) É um espelho esférico e conjuga, de um objeto real, uma imagem
real. Segundo o esquema abaixo, podemos afirmar que o espelho é:
OBJETOV
ESPELHO
IMAGEM
a)côncavo e o objeto está entre o foco e o centro de curvatura.
b)côncavo e está entre o objeto e imagem.
c)convexo e se encontra com a imagem em seu foco.
d)côncavo e o objeto está além do centro de curvatura.
e)convexo e está entre o objeto e a imagem.
ABORDAGEM ANALÍTICA
REFERANCIAL DE GAUSS
LUZ INCIDENTE
C
LUZ INCIDENTE
F
V 0
0 V
F
C
1ª Eixo das abscissas se posiciona sobre o eixo principal do espelho esférico
2ª Eixo das ordenadas se posiciona perpendicularmente ao eixo principal do espelho
esférico
0 – origem dos eixos
f – abscissa do foco (distancia focal)
R – abscissa do centro de curvatura
0 V
F
C
R
OBS:. A distancia do centro do curvatura ao vértice é a metade da distancia focal,
que vai do foco ao vértice, ou seja:
f = R
2
O – tamanho do objeto
p – distancia do objeto ao vértice
p’– distancia da imagem ao vértice
i – tamanho da imagem
O
p
0 V
F
C
P’
i
O AUMENTO LINEAR TRANSVERSAL
A = i
O
EQUAÇÃO DOS PONTOS CONJUGADOS (EQUAÇÃO DE GAUSS)
Esta equação relaciona os elementos p, p’ e f :
1
=
1
f
+
1
p
p’
EXERCÍCIO DE APLICAÇÃO
Colocou-se diante de um espelho esférico de Gauss um objeto extenso,
perpendicularmente a seu eixo principal. Sua imagem formou-se a 2,0cm do espelho; é
direita e tem metade da altura do objeto. Determine:
a)a abscissa do objeto e a natureza da imagem;
b)a distância focal e a natureza do espelho.
Resolução
a) Sabendo-se que a imagem formada do objeto real e direita concluímos que ela só
pode ser vietual
A =
I
O
b)
=
I = +1
O
2
- P’
P
1
= 1
f
p
- (2,0)
P
+ 1
p’
P = + 4,0cm (abscissa do objeto)
1 = 1
f
- 1
4,0
2,0
f = - 4,0cm
EXERCÍCIOS
1ª Questão
Um objeto real, que está a 20cm de um espelho esférico, conjuga uma imagem real a 30cm
do mesmo. Determine:
a)a distância focal
b)a natureza do espelho
2ª Questão
Um espelho esférico convexo, de 30cm de distância focal, conjuga uma imagem a 5cm do
seu vértice. Calcule a distância do objeto ao espelho.
3ª Questão
Um objeto colocado diante de um espelho esférico côncavo, de distância focal 45cm, tem
conjugada uma imagem invertida; sua altura é o dobro da do objeto. Calcule:
a)a distância do objeto ao espelho.
b)a distância da imagem ao espelho.
4ª Questão
Um espelho esférico côncavo tem raio de curvatura igual a 1m. Uma lâmpada de 2cm de
tamanho é colocada a 60cm do espelho.
Determine:
a)o aumento linear transversal da imagem;
b)o tamanho da imagem.
5ª Questão
Um objeto está colocado a 10cm do vértice de um espelho esférico convexo, de distância
focal 40cm. Determine a distância da imagem ao espelho.
6ª Questão
Uma pessoa, a 40cm de um espelho côncavo, vê a imagem do seu próprio rosto aumentada
(de três vezes) e dereita. Qual a distância focal do espelho?
REFRAÇÃO
Definição: A refração é a passagem da luz de um meio para outro.
OBS:. Se temos um meio transparente, totalmente homogêneo e isótropo denominamos de
meio refringente. Se tivermos um sistema formado por dois desses meios denominamos de
dioptro.
ÍNDICE DE REFRAÇÃO ABSOLUTO (η)
Este índice é obtido através da relação entre a velocidade da luz no vácuo(c) e a velocidade
da luz (v) no meio considerado, ou seja.
c
η=
v
Podemos verificar que este índice é adimensional e maior que um (η) já que a que não
existe velocidade maior do que a velocidade da luz no vácuo.
c
N
1(vácuo)
S
2
v
INDICE DE REFRAÇÃO RELATIVO
Supomos que a luz atravesse dois meios diferentes que não seja o vácuo.
v1
1
S
2
v2
η1 = c
v1
η2,1
=
η1
η2
η2 = c
v2
=
c/v1
c/v2
η2,1
=
η1
η2
=
v1
v2
η1 – índice de refração no meio 1
η2 – índice de refração do meio 2
v1 – velocidade da luz no meio 1
v2 – velocidade da luz no meio 2
η1,2 – índice de refração do meio 2 em relação ao meio 1
EXECÍCIOS
1ª Questão
Um raio de luz passa do ar para a água cujo índice de refração absoluto é 1,33. Determine a
velocidade de propagação da luz na água.
2ª Questão
A velocidade de propagação da luz amarela no vidro é 2/3 da velocidade de propagação da
luz no vácuo. Qual o índice de refração absoluto desse meio?
3ª Questão
A velocidade de propagação da luz amarela no vidro é 2/3 da velocidade de propagação da
luz no vácuo. Na água, é 3/4 da velocidade de propagação da luz no vácuo. Determine o
índice de refração do vidro em relação à água.
4ª Questão
A velocidade de propagação da luz amarela no óleo é 2.108m/s e na água é 2,25.108m/s,
determine:
a)o índice de refração absoluto do óleo;
b)o índice de refração absoluto da água;
c)o índice de refração do óleo em relação à água
d)o índice de refração da água em relação ao óleo.
LEI DA RAFRAÇÃO
Podemos inicialmente considerar uma um raio de luz monocromático que se propaga do
meio 1 para o meio 2 atravessando uma superfície S onde sofre refração ao incidir no meio
2
N
I
î
r
R
I - raio incidente
R - raio refratado
N- reta normal
i - ângulo de incidência
r- ângulo de refração
1ª Lei: O RAIO DE INCIDENCIA O RAIO DE REFRAÇÃO E A RETA NORMAL SÃO
COPLANARES (ou seja fazem parte do mesmo plano).
2ª Lei: LEI DE SNELL-DESCARTES
O produto do índice de refração do meio onde o raio se encontra pelo seno do ângulo que
esse raio faz com a reta normal (ângulo de incidência î) é igual ao produto do índice de
refração do meio onde o raio refrata pelo seno do ângulo que o raio refratado faz com a reta
norma (ângulo de refração r).
η1 . senî = η2. senr
senî
senr
=
η2
η1
=
η2,1
Temos por tanto dois casos a serem analisados
1ª O sistema e formado dois meios tas que: η2 > η1
N
I
î
1
2
r
v2 < v1
R
O meio 1 é menos refringente que o meio 2 neste caso: v2 < v1
2ª O sistema e formado dois meios tas que: η1 > η2
I
N
î
1
2
S
r
R
O meio 1 é mais refringente que o meio 2 neste caso: v2 > v1
EXERCÍCIOS
1ª Questão
Um raio de luz pasa do meio 1 para o meio 2 conforme indica a figura. Se η1=1 e
√2, determine o ângulo r e o desvio sofrido pelo raio de luz.
η=
I
45°
1
2
S
1
2
S
1
2
S
r
R
2ª Questão
Um raio de luz forma ângulos conforme a figura:
I
30°
ar
meio x
60°
R
Sendo ηar= 1 e var= 3.108m/s, determine:
a)o índice de refração do meio x
b)a velocidade de propagação da luz no meio x.
3ª Questão
Um raio de luz forma ângulo conforme a figura:
I
45°
r
Sabendo que v1 = 300.000 km/s e v2 = 150.000√2 km/s, calcule o ângulo de refração r.
4ª Questão
Um raio de luz passa do meio 1 para o meio 2, conforme a figura:
I
60°
1
2
S
30°
R
Sabendo-se que a velocidade de propagação da luz no meio 1 é √12x . 108m/s, determine:
a)o índice de refração no meio 1;
b)a velocidade de propagação da luz no meio 2;
c)o índice de refração no meio2
5ª Questão
(MACK) A velocidade da luz no vidro é 2/3 da velocidade da luz no vácuo. O índice de
refração absoluto no vidro vale:
a)5/2
b)5/3
c)3/2
d)4/3
e)2/3
6ª Questão
(FGV)Uma criança que olha por cima de um aquário é vista por um peixe. O peixe verá a
cabeça da criança:
a)acima do local onde ela realmente se encontra.
b)abaixo do local onde ela realmente se encontra.
c)no exato local onde ela realmente se encontra.
d)caso não haja interferência luminosa.
e)maior que a verdadeira devido à combinação da refração com a reflexão.
7ª Questão
(MACK) O índice de refração da água em relação ao vidro é 8/9. Sabendo que o índice de
refração absoluto da água é 4/3 e que a velocidade da luz no vácuo é 3.108m/s, podemos
afirmar que a velocidade d luz no vidro é:
a)2,5.108m/s
b)2,0.108m/s
c)1,5.108m/s
d)1,0.108m/s
e)0,8.108m/s