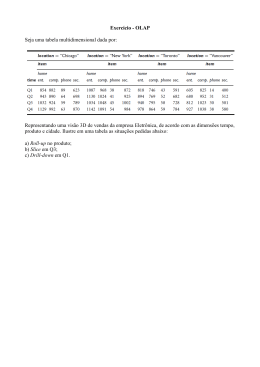
RELAÇÃO ENTRE A INTENSIDADE DE CHUVA MÉDIA EM ÁREA E PARÂMETROS DA
DISTRIBUIÇÃO DO TAMANHO DE CORDAS DE CÉLULAS DE CHUVA: PARTE II - IMPLICAÇÕES NA
UTILIZAÇÃO DE SENSOR MICROONDAS A PARTIR DE PLATAFORMA ESPACIAL.
Ricardo Sarmento Tenório
Universidade Federal de Alagoas - Departamento de Meteorologia
Cidade Universitária - 57072-970 - Maceió – AL
E-mail: [email protected]
Henri Sauvageot
Université Paul Sabatier – Laboratoire d’Aerologie
14, avenue Edouard Belin, 31400 Toulouse France
E-mail : [email protected]
Byung Hyuk Kwon
Universidade Federal de Alagoas - Departamento de Meteorologia
Cidade Universitária - 57072-970 - Maceió – AL
E-mail: [email protected]
ABSTRACT
It was demonstrated that an explicit knowledge of the rain cell diameter distribution DDCC is not necessary to
obtain the area-averaged rain rate <R>. The DDCC can be replaced by the distribution of the chords of the rain cells
(DCCC). The moments of the DCCC are analytically related to the moments of the DDCC. Thus, an equation showing
that <R> is a function of the only area-averaged chord length is given. Based on this relation, a very simple method for
the measurements of precipitation from the random intersect of the rain cell population by a scanning remote sensor is
proposed. In this method, <R> is inferred from the simple estimation of the area-averaged chord length observed, for
example, with a radar sampling, in a binary way, a rain cell distribution thresholded at mean rain rate τ. It was
suggested that this method can be implemented for area-average rain-rate estimates from a spaceborne microwave
sensor.
INTRODUÇÃO
Já foi demonstrado que a intensidade de chuva média em área (ou frações de área onde a intensidade de chuva
é superior a um determinado valor) e os parâmetros da distribuição dos tamanhos de células de chuva obedecem uma
relação muito simples (Tenório et al., neste volume). Esta relação foi apresentada de forma clara e de fácil
compreensão, calculando-se apenas alguns parâmetros do campo de chuva, por exemplo, através de um radar terrestre.
Porém, a resolução espacial da observação do radar tem um limite baixo (Tenório, neste volume) de tal modo
que a distribuição do diâmetro de células de chuva (DDCC) observada ficará truncada (t) à esquerda em D = Dt.
Tenório et al. (neste volume) mostraram que (NT )t e (<D>)t os valores parciais calculados à partir de uma DDCC
truncada, podem ser corrigidos através de um fator de correção (FC) para os momentos da DDCC obtida a partir de
dados truncados, isto é, multiplicando (NT)t e (<D>) por eλDt e (Dtλ +1)-1, respectivamente, e obtendo assim,
[
π
< R >= ( S (τ ) )( N T ) t (< D >) 2 e λDt ( λD t + 1) −2
2
]
(1)
O objetivo do presente trabalho é mostrar que, a partir da equação (1), as estimativas de <R> podem ser
deduzidas desde que se conheça m0 e m1, momentos estatísticos de ordem zero e um, de uma DDCC. E ainda que, para
o cálculo destes momentos, uma determinação explicita da DDCC não será mais necessária. Também foi sugerido que
este método possa ser implementado para estimativas de intensidade de chuva através de um sensor microondas a
2035
bordo de plataformas espaciais. Foram apresentados alguns testes e simulações a partir de dados de radar terrestre para
apoiar a validação da proposta.
CÁLCULO DE <R> A PARTIR DA DISTRIBUIÇÃO DA CORDA DE CÉLULA CHUVA.
Figura 1 - Representação esquemática de uma
plataforma espacial movendo-se ao longo de uma
trajetória T e fazendo uma amostragem do campo
de chuva em forma células circulares. O sensor
microonda faz uma varredura perpendicular a T, no
sentido das linhas retas mais claras. Os segmentos
escuros são as cordas observadas.
Considere-se um conjunto de janelas distribuídas ao
longo de uma varredura azimutal de um radar com baixo ângulo de elevação, através de um campo de células circulares
de chuva (isto é, varredura PPI clássica). Da mesma maneira,
também pode-se considerar (Figura 1) uma plataforma espacial que descreve uma trajetória (T) e através de um sensor
microondas a bordo, realiza uma varredura com trilhas não
adjacentes (nonadjacent swaths), perpendicularmente a T, e
sobre de um campo de células circulares de chuva. O que é
executado pelo sensor é uma amostragem aleatória das cordas
l, resultado da intercepção do feixe do sensor pelas células de
chuva (no caso de uma varredura PPI, o arco de um de círculo
pode ser aproximado pela tangente). A interpretação estatística da amostragem das cordas, em termos de DDCC, requer
o conhecimento da relação entre a distribuição de cordas de
célula de chuva (DCCC) e a DDCC. A derivação desta relação foi realizada pela primeira vez por Wicksell (1925)
quando deduziu a distribuição de corpúsculos esféricos embutidos em tecido orgânico, cortado por um plano arbitrário
que interceptavam estes corpúsculos. Utilizando o mesmo
método, Vul'fson (1961) inferiu a distribuição do tamanho de
células convectivas utilizando-se das flutuações de temperatura observadas a partir de um avião em trajetória reta e horizontal dentro de uma atmosfera de convectiva. A mesma
aproximação também foi usada por Yau e Rogers (1984),
quando discutiram a distribuição do tamanho de áreas de
chuva utilizando dados de pluviômetros. Vul'fson (1961)
mostrou que momentos de ordem p da função de distribuição
de probabilidade da corda, gp, e os momentos de ordem p + 1
da DCCC, mp + 1, estão relacionados por
g p = C( p)
m p+1
m1
(2)
,
onde C(p) é um coeficiente, tal que
−1
1  p   1    p + 3 
C ( p ) = Γ + 1Γ  Γ 
 ,
2 2
  2    2 
(3)
e Γ é a função gama; para p = 1, C(p) = π/4.
Sabe-se que <D> pode ser obtido através de Tenório et al., equação 07, neste volume, isto é,
< D >=
1
NT
∞
∫0
DN ( D, τ )dD =
2036
m1
,
m0
(4)
Logo, para p = 1, e utilizando as equações (4) e (3) em (2), obtêm-se
m2 =
4 NT
g1 .
π λ
(5)
Segundo Tenório et al. (neste volume), o diâmetro médio de células de chuva em área é proporcional a λ -l,
logo:
D =
1
.
λ
(6)
Vul'fson (1961) e Yau e Rogers (1984), em suas aproximações, afirmaram que o número médio de células com
qualquer diâmetro, interceptadas por uma linha L, isto é o número médio de cordas, é dado por:
∞
n = LA −1 N T ∫ Dn(d )dD = LA −1 N T < D > .
(7)
0
Usando (4) e (6) em (7), pode-se escrever;
(8)
NT
n
= ,
λ
L
onde aqui, L é o comprimento da trajetória de medida do sensor distante e n o número de cordas observadas associadas
a L.
Pode-se calcular g1 através do cálculo das médias das cordas <l>, observadas dentro de uma área A, em um
campo de células chuva com intensidades R = τ, onde valores de R<τ são desprezados. Assim, utilizando as equações
(8) e (5), obtêm-se
m2 =
4n
< l >.
π L
(9)
Como visto para os dados de radar, a resolução espacial do sensor microondas tem um mais baixo limite l0, de
tal modo que a DCCC observada é truncada à esquerda em l = l0. Assim, <l> na equação (9) também tem que ser
corrigido em função do truncamento. É aceitável assumir que a distância x entre uma corda e o centro de uma célula, é
distribuída uniformemente entre zero e D/2. Então, se a distribuição D for representada corretamente por uma
distribuição exponencial (Tenório, neste volume), a distribuição de cordas será de forma exponencial.
Logo, a DCCC pode ser escrita da seguinte forma
w(l ,τ ) = w0 (τ )e −αl ,
(10)
onde w0(t) e α são os parâmetros da DCCC.
As inclinações da DDCC e DCCC, λ e α, estão relacionadas. A relação é obtida facilmente, escrevendo-se a
equação (2) para p =1. Quer dizer, g1 = C1 m2/m1. A partir da integração da equação do enésimo momento estatístico de
uma distribuição de N (D, τ) (Tenório et al., neste volume), obtêm-se
mn (τ ) = N 0 (τ )
n!
.
λn +1
Logo, a partir de (11), pode-se obter m2/m1 = 2/λl e g1 = a-1. Com C1 = π/4, obtêm-se
2037
(11)
α=
(12)
2
λ ≅ 0,64λ .
π
Utilizando-se das aproximações para a correção dos parâmetros (fator de correção FC) da distribuição
calculadas a partir de uma DDCC truncada Tenório et al. (neste volume), pode-se mostrar que n e <l>, o número total
de cordas e o comprimento médio das cordas, calculados a partir de uma DCCC truncada à esquerda em l = lt, são
(13)
n = n eαlt
t
e
< l >= (< l > )t (αl t + 1) ,
−1
(14)
onde o subscrito t refere-se ao truncamento.
Como pode-se verificar, a equação (9) pode ser reescrita da seguinte forma
m2 =
(15)
4 nt
(< l >)t eαl (αlt + 1)−1 .
π L
t
Através da equação proposta por Tenório et al. (neste volume), para a estimativa da intensidade média de
chuva em área
(16)
π
< R >= S (τ ) m2 ,
4
e da equação (15), a intensidade média de chuva em área dentro de uma área A observada é
[
< R >= S (τ )e αl (αl t + 1) −1
t
] nL (< l >) .
t
Figura 2 - Distribuição típica do comprimento de corda w(l,τ)
deduzido a partir dos dados do radar de Niamey (Niger). l é o
comprimento da corda, τ é o limiar da taxa de chuva. A linha reta é o
ajuste realizado com (26); α é a inclinação exponencial, ρ é o
coeficiente de correlação, e A é a área observada. O espaçamento entre
as linhas retas (trajetória do sensor) é de 15 km.
2038
(17)
t
Observando esta equação, nota-se
que os parâmetros localizados entre
colchetes são todos conhecidos. Então,
conhecendo-se a relação entre o número
total (truncado) de cordas, o comprimento
da trajetória e o comprimento médio das
cordas, pode-se obter intensidade média
de chuva em área, dentro de uma
determinada área observada, <R>.
De maneira similar F (τ), a fração
de área ocupada pelas células de chuva
para intensidades de chuva acima de um
limiar τ, por unidade de área, pode ser
obtida dividindo-se <R> por S (τ), pois
<R> está estatisticamente relacionada à
F(τ) por uma relação linear da forma
R = S (τ )F (τ ) (Doneaud et al., 1984;
Chiu, 1988; Lopez et al., 1989; Atlas et
al., 1990; Rosenfeld et al., 1990; Kedem
et al., 1990; Cheng e Brown, 1993;
Sauvageot, 1994; Ramos-Buarque e
Sauvageot, 1997; Chèze e Sauvageot,
1997).
3 - TESTES EXPERIMENTAIS
Alguns testes experimentais foram efetuados com o objetivo de demonstrar a validade das equações propostas
neste trabalho. O conjunto de dados utilizados consiste em dados de radar banda C, coletados em latitudes tropicais em
Niamey (Níger - África Ocidental), e em latitudes médias em Toulouse, (sudoeste da França). Os campos de chuva
deduzidos das medidas de refletividade radar foram calibrados a partir de uma rede pluviométrica. As informações
detalhadas sobre as condições de observação de Niamey estão descritas em Tenório et al. (1995) e Tenório (1996) e de
Toulouse, em Tenório et al. (neste volume) e Tenório (1996).
Os primeiros testes concernem à forma das distribuições de cordas. Usando o conjunto de dados do radar de Niamey, foram geradas linhas retas paralelas, através de varreduras PPIs, quando então as DCCCs foram elaboradas. A
Figura 3 mostra, como um exemplo das DCCCs obtidas, os resultados para um limiar de 2,72 mm h-1 com um espaçamento entre as linhas retas de 15 km. Na Figura 2, a inclinação α foi 0,15 km-1 e o coeficiente de correlação do ajustamento a uma distribuição exponencial foi ρ = 0,97. Os resultados (Tabela 1) dão suporte à conclusão esperada, isto
é, que as DCCCs são semelhantes as DDCCs, especialmente no que se refere à forma exponencial, com uma inclinação
pouco dependente de τ, e que o fator de correção proposto por Tenório et al. (neste volume) [veja (14)], isto é, CF =
(αlt+1)-1, satisfaz a razão <l>/<l>t .Também a razão α/λ é muito próxima do valor teórico obtido com a equação (14),
que é 0,64.
Tabela 1 - Testes dos parâmetros da distribuição de cordas de células de chuva observadas em Niamey em 1993. As
DCCCs são representadas por uma distribuição exponencial equação (10); τ é o limiar de taxa de chuva, α é a
inclinação da DCCC, ρ é o coeficiente de correlação da DDCC ajustada, <l> e <l>t, são os comprimentos médios das
cordas calculadas usando-se todas as cordas observadas e com um truncamento esquerdo em lt = 5 km. FC = (αlt+1)-1 é
o fator de correção (FC) da equação (14), isto é, FC é a inclinação das DDCCs para comparação com α.
<l>
<l>t
<l> /<l>t
FC
τ
α
ρ
λ
α /λ
λ
-1
-1
-1
(km)
(km)
(mm h )
(km )
(km )
0,13
0,14
0,94
6,39
9,83
0,65
0,59
0,20
0,70
0,36
0,14
0,94
6,39
9,83
0,65
0,59
0,19
0,74
1,00
0,14
0,95
6,28
9,72
0,65
0,59
0,22
0,64
2,00
0,15
0,97
6,19
9,49
0,65
0,57
0,20
0,75
2,72
0,15
0,97
6,24
9,53
0,65
0,57
0,21
0,71
4,00
0,15
0,97
6,12
9,42
0,65
0,57
0,19
0,79
5,00
0,16
0,96
6,01
9,37
0,64
0,55
0,20
0,80
6,00
0,16
0,96
5,89
9,34
0,63
0,55
0,21
0,76
Tabela 2 - Testes da equação (15); τ é o limiar de chuva, ρ é o coeficiente de correlação, e C é o coeficiente de
proporcionalidade, com C0 = observado e Cc = calculado.
C0
Cc
Local
τ
ρ
(mm h-1)
(mm h-1)
(mm h-1)
2,72
0,86
35
27
4,0
0,77
39
29
5,0
0,89
45
31
Niamey
6,0
0,91
50
34
(1993)
7,5
0,92
56
36
Toulouse
(1996)
0,36
1
2
2,72
3
3,5
4
<0
0,16
0,75
0,81
0,81
0,48
<0
2039
12
12,5
16,6
19,9
22,1
26,1
34,5
2,6
4,4
9,6
15,1
17,3
22,3
27,3
O segundo teste realizado é em relação à equação (17). A partir dos dados de Niamey, e de Toulouse, os pares
experimentais <R> e U, com
(`18)
U = nt L−1 (< l >) t ,
foram calculados e plotados na Figura 3, para testar a equação (17) escrita na seguinte forma
< R >= C0U ,
(19)
onde C0 é o valor do coeficiente de proporcionalidade observado. O ajustamento foi realizado forçando a ocorrência de
zero intercepção, como implica a equação (17). Se S(τ) for conhecido, através da equação (17), pode-se calcular um
valor para o coeficiente de proporcionalidade Cc , isto é,
C c = S (τ )eαlt (αlt + 1) −1 .
(20)
Os valores de C0, Cc como também o
coeficiente de correlação do ajustamento dos dados
observados e plotados na Figura 3, são mostrados na
Tabela 2. Os valores de Cc foram calculados
utilizando-se os valores de S(τ) computados através de
dados de disdrômetro, em chuvas ocorridas no local ou
próxima dos sítios das observações do radar
(Sauvageot, 1994).
Os valores de C0 e τ estão relacionadas de
forma linear:
- Para Niamey: C 0 = 4, 2τ + 24 ,
(21)
com C0 e τ em mm h-1 e um coeficiente de correlação
ρ = 0,9.
- Para Toulouse C 0 = 6,5τ + 2,8 ,
(22)
com ρ = 0,9.
Os resultados apresentados na Tabela 2
mostram que, para τ em torno de 7,5 mm h-1 em
Niamey e 3 mm h-1 em Toulouse, <R> e U estão bem
correlacionados, principalmente para Niamey (ρ >
0,9). Os valores de C0 e Cc são semelhantes para
Toulouse, mas para Niamey apresentam discrepância
de aproximadamente um fator de 1,5. Esta divergência
pode ser a falta de representatividade dos valores S(τ)
usados para na computação de Cc , visto que, para τ ≥
5 mm h-1, a maioria da parte estratiforme das linhas de
Figura 3 – Intensidade de chuva média em área <R> em
instabilidade (squall lines ), o tipo principal de sistema
função de U = nt L-1 (<l>), onde nt é o número total de
de chuva forte em Niamey, foi suprimida das
cordas, L é o comprimento da trajetória de varredura do
estatísticas. Assim, o valor satisfatório pode ser mais
sensor, e (<l>) é o comprimento médio da corda. U é um
alto que o valor computado a partir dos dados do
número sem dimensão. As retas são curvas ajustadas, τ é
disdrômetro. Finalmente, concluiu-se que o método
o limiar e ρ é o coeficiente de correlação.
que usa a equação (17) é funcional. Os resultados dos
testes apresentados na Tabela 2 não são suficientes nem definitivos para se avaliar plenamente a utilidade da equação
(17) para medidas de chuva, porém, podem ser considerados como resultados iniciais encorajadores.
2040
4 - MEDIDAS DE CHUVA ATRAVÉS DE UM SENSOR MICROONDAS EM PLATOFORMA ESPACIAL
A observação da distribuição de chuva em escala global foi identificada há muito tempo como uma das chaves
principais para a compreensão do ciclo da água e de energia na circulação atmosférica. Seguindo esta orientação, a
comunidade científica criou e/ou aperfeiçoou instrumentos capazes de coletar os dados requeridos para as estimativas
dos campos de chuva, e desenvolveu métodos e algorítmos que habilitam a extração da distribuição de chuva ao nível
da superfície, a partir de dados brutos. Entre as técnicas mais relevantes para observação de chuva global, estão os
sensores microondas a bordo de plataformas espaciais: radiômetros infravermelhos e, agora, radar com Tropical
Rainfall Measuring Mission (TRMM) (Simpson et al., 1988; Meneghini e Kozu, 1990; Durden et al., 1994).
Os sistemas de sensores microondas em plataformas espaciais têm que compor os vários problemas relativos à
resolução espacial, a sensibilidade instrumental, e a precisão das medidas. Muitos algorítmos voltados à superação
dessas dificuldades, e com o objetivo de estimar a intensidade de chuva a partir dos sinais microondas espaciais, têm
sido propostos, testados e comparados através de simulação (Meneghini e Kozu, 1990; Marzoug e Amayenc, 1994;
Amayenc et al., 1996). Porém, o problema ainda não foi resolvido. Esse assunto continuar em aberto.
Os sensores microondas têm duas desvantagens principais. A primeira é a dificuldade para cobrir a toda a
extensão da área de chuva a ser medida. Isto conduziu à utilização de métodos com exigências mínimas em relação ao
intervalo de R. Por isso, o método com limiares recebeu atenção especial, pois a sua implementação requer somente a
informação se R é maior ou menor que a taxa de precipitação média. Este método foi proposto para as estimativas de
precipitação a partir de sensores microondas em plataformas espaciais e sensores infravermelhos (por exemplo, Arkin,
1979; Johard e Desbois, 1992; Atlas e Bell, 1992; Meneghini e Jones, 1993; Johnson el al., 1994).
A segunda desvantagem é o tempo necessário para executar as medidas. O campo de chuva normalmente é
observado através de uma varredura com passagens perpendiculares à direção do deslocamento da plataforma. Levando
em conta a velocidade da plataforma, a área a ser escaneada e o tempo necessário para se obter uma estimativa precisa
da refletividade radar em cada pixel, o tempo disponível é um fator crítico. Isso explica a procura por esquemas de
escaneamento capazes de reduzir o tempo de medida. Esta redução pode ser alcançada, por exemplo, utilizando-se
varreduras com trilhas não adjacentes (nonadjacent swaths). O método proposto neste trabalho talvez possa superar
estas dificuldades.
5 - ANÁLISE E CONCLUSÕES
A literatura mostra que a distribuição do tamanho de células de chuva para um limiar de intensidade de chuva τ
pode ser representada por uma distribuição exponencial na qual o parâmetro exponencial depende de localização
geográfica e é independente de τ. A partir deste resultado, foi demonstrado que, integrando a DDCC, pode-se obter
novas relações entre os momentos da DDCC e alguns significantes parâmetros do campo de chuva.
Baseado nestas relações foi proposto um novo e simples método de medida de intensidade de chuva através de
radar. O interessante desse método é que ele permite a minimização das exigências de informação para a dedução de
<R>, isto é:
- o tempo de medição é reduzido, pois o campo de chuva é observado através de uma varredura com
trilhas não adjacentes (nonadjacent swaths) perpendiculares à direção do deslocamento da
plataforma;
- o intervalo de R a ser medido é mínimo, pois é necessário somente um sensoriamento binário em torno
de um limiar τ.
Então, baseado nas simulações usando dados de radar terrestre para testar o método proposto, conclui-se que:
a) os conceitos básicos são válidos;
2041
b) que esse método oferece um grande potencial para a realização de estimativas da intensidade de
chuva média em área ou frações de área onde a intensidade de chuva é superior a um determinado
valor, através de sensor microondas a bordo de plataformas espaciais.
REFERÊNCIAS BIBLIOGRÁFICAS
AMAYENC, P., J. P. DIGUET, M. MARZOUG, T. TANI. A class of single and dual-frequency algorithms for rain
rate profiling from a spaceborne radar. Part II. Tests from airborne radar measurements. J. Atmos. Oceanic
Technol., 13, 142-164. 1996.
ARKIN, P. A.. The relationship between fractional coverage of high cloud and rainfall accumulations during GATE
over the B-scale array. Mon. Wea. Rev., 107, 1382-1387. 1979.
ATLAS, D., T. L. BELL. The relation of radar to cloud area-time integrals and implications for rain measurements
from space. Mon. Wea. Rev., 120, 1997-2008. 1992.
_____, D. ROSENFELD, D. A. SHORT. The estimation of convective rainfall by area integrals. Part 1. The theoretical
and empirical basis. J. Geophys. Res., 95 (D3), 2153-2160. 1990.
CHENG, M., R. BROWN. Estimation of area-average rainfall for frontal rain using the threshold method. Quart. J.
Roy. Meteor. Soc., 119, 825-844. 1993.
CHEZE, J. L., H. SAUVAGEOT. Area-average rainfall and lightning activity. J. Geophys. Res., 102 (D2), 1707-1715.
1997.
CHIU, L. S.. Estimating areal rainfall from rain area. Tropical Rainfall Measurements, J. S. Thepn and N. Fugono,
Eds., A.Deepak, 361-367. 1988.
DONEAUD, A. A., S. I. NISCOV, D. L. PRIEGNITZ, P. L. SMITH. The area-time integral as an indicator for
convective rain volume. J. Climate Appl. Meteor., 23, 555-561. 1984.
DURDEN, S. L., E. IM, F. K. LI, W. RICKETTS, A. TANNER, W. WILSON. ARMAR: An airborne rain-mapping
radar. J. Atmos. Oceanic Technol., 11, 727-737. 1994.
JOBARD, I., M. DESBOIS. Remote sensing of rainfall over tropical Africa using Meteosat infrared imagery.
Sensitivity to time and space averaging. Int. J. Remote Sens., 13, 2683-2700. 1992.
JOHNSON, L. R., R L. SMITH, T. H. VONDER HAAR, D. REINKE. The relationship between area-time integrals
determined from satellite infrared-data by means of a fixed-threshold approach and convective rainfall volumes.
Mon. Wea. Rev., 122, 440-448. 1994.
KEDEM, B., L. S. CHIU, Z. KAMI. An analysis of the threshold method for measuring the area-average rainfall. J.
Appl. Meteor., 29, 3-20. 1990.
LOPEZ, R. E., D. ATLAS, D. ROSENFELD, J. L. THOMAS, D. O. BLANCHARD, R. E. HOLLE. Estimation of
areal rainfall using the radar echo area time integral. J. Appl. Meteor., 28, 1 162-1174. 1989.
MARZOUG, M., P. AMAYENC. A class of single and dual- frequency algorithms for rain rale profiling from a
spaceborne radar. Part I. Principle and tests from numerical simulations. J. Atmos. Oceanic Trchnnl. 11, 14801506. 1994.
MENEGHINI. R., J. A. JONES. An approach to estimate the areal rain-rate distribution from spaceborne radar by the
use of multiple thresholds. J. Appl. Meteor., 32, 386-398. 1993.
_____, T. KOZU. Spaceborne Weather Radar. Artech House. 199 pp. 1990.
RAMOS-BUARQUE, S. H. SAUVAGEOT. The estimation of rainfall in the Sahelian squall line by the area-threshold
method. Atmos. Res.. 43, 207-216. 1997.
ROSENFELD. D.. D. ATLAS, E D. A. SHORT. The estimation of convective rainfall by area integrals. Part II. The
height-area rainfall threshold (HART) method. J. Geophys. Res., 95, (D3), 2161-2176. 1990..
SAUVAGEOT, H.. The probability density function of rain rate and the estimation of rainfall by area integrals. J.
Appl. Meteor., 33,1255-1262. 1994.
SIMPSON, J., R. F. ADLER, G. R. NORTH. A proposed tropical rainfall measuring mission (TRMM) satellite. Bull.
Amer. Meteor. Soc.. 69, 278-295. 1988.
2042
TENORIO, R. S.. Distribuição do tamanho de células da chuva. uma revisão crítica. neste volume. 2000.
_____, H. SAUVAGEOT E J. F. DE OLIVEIRA JUNIOR. Relação entre a intensidade de chuva média em área e
parâmetros da distribuição do diâmetro de células de chuva: Parte I - implicações na utilização de dados de radar.
neste volume. 2000.
_____. Etude statistique de la distribution de taille des cellules de pluie. implications pour l'estimations des
champs de précipitation par radar. Tese de Doutorado, Université Paul Sabatier – Toulouse III - França. 189 pp.
1996.
_____, H. SAUVAGEOT, S. RAMOS-BUARQUE. Statistical studies of rain cell size distribution using radar data
during squall line episodes in West Africa. Proc. Third Int. Symp. on Hydrological Applications of Weather
Radar, São Paulo, Brasil. 518-526. 1995.
VUL'FSON, N. L. Convective Motions in a Free Atmosphere. Israeli Program for Scientific Translation, 188 pp.
1961.
WICKSELL, S. D. The corpuscule problem. A mathematical study of a biometric problem, Biometrika, 17, 84-99.
1925.
YAU, M. K., R. R. ROGERS, An inversion problem on inferring the size distribution of precipitation areas from rain
gauge measurements. J. Atmos. Sci.. 41, 439-447. 1984.
2043