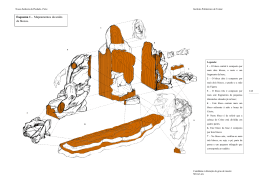
Armazenamento e Indexação
5
Nestes casos, podem evitar-se operações dispendiosas de ordenação de registos, pelo
que pode valer a pena criar índices nas colunas da cláusula WHERE com determinadas
ordenações. Como as folhas da B+-tree estão ligadas entre si, é sempre possível ler as
chaves em qualquer ordem (ascendente ou descendente).
5.6.2 Hashing 15
Uma função de hashing opera um mapeamento entre um grande conjunto de entrada e
um conjunto finito de saída. As funções de hashing são extensivamente usadas em várias
áreas da informática. No contexto da indexação, a função de hashing mapeia uma chave K
para um de n blocos, que são tipicamente as páginas no disco. Assim, várias chaves são
mapeadas para o mesmo bloco, originando uma colisão, e uma das propriedades mais
desejáveis de uma função de hashing é o mapeamento uniforme dos valores da chave por
todos os n blocos. Se um bloco for uma página do disco que contém os registos indexados, como vimos, na prática, este tipo de funções permite um acesso direto aos dados a
partir da chave. Este princípio é mostrado na Figura 5.21.
k
h(k)
0
n-1
blocos
Figura 5.21 – Função de hashing
Na prática, o valor h(k) é uma entrada do índice que contém a localização do registo ou
registos com a chave K. Se a tabela estiver organizada segundo a função de hashing,
utilizando a organização de ficheiros que vimos anteriormente, o acesso pode ser direto.
Uma função de hashing deve distribuir uniformemente os registos por todos os blocos,
e essa distribuição deve ser aleatória, isto é, deve ser independente da distribuição das
chaves, resultando no mesmo número de chaves por bloco. Deste modo, uma função de
hashing trabalha sobre valores numéricos, pelo que se o valor a indexar for alfanumérico, pode ser transformado primeiro num valor numérico, usando, por exemplo, o código
UTF-8 dos caracteres. Assim, a função será aplicada sobre este valor numérico.
Os índices que usam funções de hashing apresentam as seguintes limitações:
■■
15
Como não existe nenhuma relação de ordem entre h(k), não é possível percorrer de
forma eficiente e ordenada as chaves. Deste modo, os índices que usam hashing não
podem ser agrupados, exceto se a organização da tabela estiver também de acordo
com a função de hashing;
Hashing é, por vezes, designado em português como “dispersão”.
© FCA – Editora de Informática
159
FUNDAMENTOS DE BASES DE DADOS
■■
Não é possível utilizar funções de hashing para consultas com intervalos de valor,
apenas para condições de igualdade.
Por outro lado, as funções de hashing são muito eficazes para testes de igualdade, pelo
que são também bastante usadas no processamento de equijunções.
Por exemplo, se a distribuição de chaves for uniforme, uma função de hashing simples e
com um comportamento aceitável usa o resto da divisão por n; sendo dado um valor da
chave, o bloco em que este se encontra é dado pelo resto da divisão por n. Outra função
de hashing divide a chave em várias partes e calcula o “ou exclusivo” de todas as partes.
Se a distribuição de chaves não for uniforme, alguns blocos terão tendência a ficar preenchidos mais rapidamente do que outros e poderemos ter uma situação em que não podem
aceitar mais chaves. É também possível que o número de chaves ultrapasse a capacidade
total dos n blocos. Nesse caso, devem utilizar-se blocos adicionais, ligados ao bloco que ficou preenchido, mas já não é possível continuar a aceder aos dados num único acesso. Se
os blocos adicionais ficarem totalmente preenchidos, é necessário ligar-lhes mais blocos
adicionais, com o consequente aumento do número de acessos, o que traz rapidamente
problemas de desempenho. Uma solução consistiria em juntar mais blocos principais, mudar a função de hashing para prever o novo número de blocos e reindexar todas as chaves
– contudo, na prática, esta solução seria custosa e não é exequível.
Esta técnica de hashing – hashing estático – apresenta os seguintes inconvenientes para
a sua utilização em indexação:
■■
O número n de blocos deve ser, à partida, corretamente dimensionado, caso contrário, é necessário recorrer à utilização de blocos adicionais ligados aos preenchidos;
■■
Se o número inicial de blocos for aumentado, tem de se alterar a função de hashing
e, consequentemente, reindexar todas as chaves.
Para evitar a utilização de blocos adicionais devidos ao preenchimento de alguns blocos,
ou seja, para adaptar o número de blocos às características da base de dados ao longo do
tempo, foram propostas as seguintes técnicas de hashing dinâmico:
■■
Hashing extensível;
■■
Hashing linear.
Vamos ver a seguir estas duas técnicas.
5.6.2.1 Hashing extensível
O hashing extensível foi proposto por Fagin et al. (1979). Esta técnica aumenta o número
de blocos disponíveis em caso de preenchimento, em vez de utilizar blocos ligados, e evita
a reindexação de todas as chaves. Desta forma, continua a manter-se uma única leitura
para acesso aos dados, sem o inconveniente de reorganizar as chaves existentes. Esta
técnica usa os seguintes princípios:
■■
160
A função h(k) tem b bit dos quais apenas os i menos significativos são utilizados;
© FCA – Editora de Informática
Armazenamento e Indexação
■■
5
Um diretório com 2i apontadores permite o acesso aos registos no disco.
O diretório tem um nível global, que é o número i de bit usado para endereçar as chaves.
Cada bloco tem um nível local j, que é o número de bit usado para colocar as chaves nesse
bloco. Quando um bloco fica preenchido como resultado da inserção de um novo registo
com chave K, podem ocorrer duas situações:
■■
O nível local j do bloco é inferior ao nível global do diretório. Nesse caso, divide-se o
bloco usando os j +1 bit e repartindo os registos entre os dois blocos. O nível local
dos dois blocos passa a ser j +1;
■■
O nível local j do bloco é igual ao nível global i do diretório. Nesse caso, incrementa-se
i duplicando o número de entradas no diretório e substituindo cada entrada por duas
que apontam para o mesmo bloco. Calcula-se o novo valor da chave K e, como i é
agora superior ao j do bloco, procede-se como na situação anterior.
O tamanho do diretório permite que a sua duplicação seja uma operação rápida e não penalize o desempenho. Vamos considerar que a função de hashing usa apenas o bit menos
significativo (i = 1). A Figura 5.22 mostra um exemplo com três registos mapeados em
dois blocos.
k
h(k)
010
i=1
0
010
1
101
111
diretório
blocos
j=1
j=1
Figura 5.22 – Hashing extensível
O diretório usa apenas um bit para colocar o hashing da chave nos dois blocos; repare-se
que as duas chaves com o bit menos significativo a 1, 101 e 111 são colocadas no mesmo
bloco. Vamos supor que a capacidade dos blocos é de 2. A inserção do valor 001 seria feita
num bloco preenchido com um nível local igual ao nível global, por isso o diretório tem de
ser duplicado, como mostrado na Figura 5.23.
k
00
h(k)
i=2
001
010
01
101
001
10
blocos
11
111
diretório
novo bloco
j=1
j=2
j=2
Figura 5.23 – Duplicação do diretório
Repare-se que como usamos os bits menos significativos, duplicar o diretório consiste
apenas em copiá-lo, uma vez que os apontadores mantêm a sua posição. Depois de duplicado, procede-se à inserção do valor no bloco correspondente provocando a sua divisão e
a atualização dos apontadores no diretório. Com efeito, o número de blocos não duplica,
sendo que tal apenas se verifica no número de entradas no diretório.
© FCA – Editora de Informática
161
FUNDAMENTOS DE BASES DE DADOS
Caso uma entrada seja removida, pode remover-se o bloco correspondente se este ficar
vazio. Senão, e se a sua ocupação for mínima, pode tentar-se uni-lo com outro bloco que
tenha o mesmo nível local e os mesmos bits menos significativos. Regra geral, não compensa reduzir o tamanho do diretório, exceto se o número de chaves diminuir significativamente.
Quando o número total de bits for usado, não é possível duplicar mais o diretório. Neste
caso, recorre-se a blocos ligados, o que também pode acontecer se se tiver imposto um
limite nas duplicações do diretório. Se a função de hashing produzir um enviesamento
na distribuição das chaves, podemos ter um número reduzido de blocos a ser constantemente dividido e a atingir rapidamente o limite de duplicações do diretório. Neste caso, o
interesse do hashing extensível é reduzido.
Para ultrapassar estes inconvenientes, foi proposto o hashing linear, que veremos a seguir.
5.6.2.2Hashing linear
As técnicas de hashing linear (Litwin, 1980) usam uma família de funções hi, em que cada
uma mapeia as chaves para o dobro dos blocos da anterior – este efeito é semelhante à
duplicação do diretório no hashing extensível. Se h1 gere n blocos, h2 gere 2 n blocos e
assim por diante. Regra geral, hi gere 2i × n blocos, numerados de 0 a 2i × n−1.
Um exemplo de uma família de funções com estas características usa o resto da divisão
por 2i × n, sendo i = 0, 1, 2,…e n o número inicial de blocos.
Vamos considerar que inicialmente i = 0 e seguinte = 0. O critério de divisão de blocos
pode ser ultrapassar uma percentagem máxima de preenchimento, de um número máximo de blocos ligados ao preenchido, ou qualquer outro critério que se queira definir.
Deste modo, o critério de divisão é flexível e permite, se necessário, minorar os efeitos de
reorganização do índice.
Se a inserção de uma nova entrada preencher o critério de divisão de blocos, procede-se
da seguinte forma:
1. Divide-se o bloco da posição seguinte, mesmo que não seja o bloco que preencheu
o critério de divisão, e cria-se um novo bloco na posição 2i × n + seguinte.
2. Redistribuem-se as entradas do bloco seguinte, usando hi + 1; algumas entradas permanecerão, outras serão deslocadas para o novo bloco.
3. Incrementa-se seguinte de uma unidade. Assim, todos os blocos inferiores a seguinte foram reindexados.
Por seu lado, a pesquisa de chaves deve testar primeiro se o bloco resultante já foi reindexado:
■■
Se hi(k) < seguinte, o bloco já foi dividido, deve reindexar a chave com hi+1(k);
■■
Se hi(k) ≥ seguinte, o bloco ainda não foi dividido, pode ser utilizado.
162
© FCA – Editora de Informática
Armazenamento e Indexação
5
Repare-se que se pode atingir o limite seguinte > 2i × n – 1. Neste caso, todas as chaves
já foram reindexadas com a função do nível seguinte hi+1. Assim, incrementa-se o nível i e
coloca-se seguinte a 0, recomeçando então a partir do primeiro bloco.
Em qualquer instante, a estrutura de hashing linear tem a separação de blocos para um
determinado nível i apresentada na Figura 5.24.
0
blocos
divididos (hi+1)
seguinte
hi
hi+1
blocos não
divididos (hi)
2i × n−1
blocos
divididos (hi+1)
Figura 5.24 – Hashing linear
Note-se que o nível seguinte permite utilizar até ao dobro dos blocos, mas isto só é feito
de forma linear, um bloco de cada vez, e quando necessário, isto é, quando há divisões.
Desta forma, o hashing linear pode utilizar menos memória do que o hashing extensível.
Como a divisão de blocos é sempre sequencial, na posição seguinte, todos os blocos
poderão eventualmente ser divididos, o que também evita longas listas de blocos ligados.
Com efeito, no hashing extensível, poderia haver concentração de divisões num número
reduzido de blocos, devido ao enviesamento das chaves ou da função de hashing.
5.7 Índices Mapa de Bits
Um índice mapa de bits (O’Neil e Quass, 1997) usa um mapa16 de bits, em que cada bit corresponde a um valor possível do atributo indexado. Para um determinado tuplo e atributo
indexado, o bit k é 1 se o k-ésimo valor estiver no atributo desse tuplo, caso contrário é 0.
O mapa de bits permite uma representação compacta dos valores presentes no atributo,
e é tanto mais eficaz quanto menos valores únicos existirem para esse atributo. Este tipo
de índices permite também a representação de valores nulos, o que não acontece com os
índices arborescentes.
16
Concetualmente é um vetor. Este tipo de índices foi inicialmente proposto no protótipo de armazém de dados Model 204, nos anos 70
(O’Neil, 1987).
© FCA – Editora de Informática
163
FUNDAMENTOS DE BASES DE DADOS
Exemplo 5.1
Um exemplo de um mapa de bits é mostrado na Tabela 5.2. Existindo quatro valores distintos para um dado atributo (A, B, C, D), o mapa usa 4 bits para marcar a presença de cada um.
Tabela 5.2 – Exemplo de mapa de bits
registo
atributo
b1
b2
b3
b4
r1
A
1
0
0
0
r2
B
0
1
0
0
r3
A
1
0
0
0
r4
D
0
0
0
1
Para responder a uma consulta “>= B”, bastaria aplicar um operador binário – OU – à parte
do mapa que codifica valores maiores ou iguais a B: (b2 OU b3 OU b4). Como as operações
binárias são muito rápidas, testar a restrição é geralmente muito rápido, o que faz com que
este tipo de índices seja atrativo nestes casos. O índice pode ser usado também na “horizontal”, permitindo conhecer o valor do atributo de qualquer um dos registos.
Se o número de valores distintos for muito grande, o mapa também será, pelo que se
desenvolveram técnicas de compressão de valores (O’Neil et al., 2007) e de utilização de
intervalos de valores para reduzir o número de mapas (Wu e Yu, 1998). Atualmente só
o Oracle, o MySQL e o Sybase IQ permitem índices com mapas de bits; outros SGBD
usam-nos internamente, por exemplo, para acelerar junções devido à sua rapidez, mas não
os permitem como índices definidos pelo utilizador.
Estes índices implicam geralmente um acesso aos tuplos no disco, enquanto uma B-tree
pode permitir acessos apenas ao índice. Regra geral, um mapa de bits é vantajoso se:
■■
A tabela a indexar contiver linhas na ordem das dezenas de milhão;
■■
Na prática, o número elevado de condições de consulta impedir a definição de todos
os índices B-tree que seriam necessários.
Estas características tornam este tipo de índices essencialmente atrativos para aplicações
analíticas de suporte à decisão, com consultas muito variadas e grandes quantidades de
tuplos – situações em que a utilização de diversos índices B+-tree muito grandes seria
ineficaz.
5.8 Generalized Search Tree (GiST)
Hellerstein, Naughton e Pfeffer (1995) propuseram uma estrutura arborescente genérica e
equilibrada que pode ser parametrizada para implementar qualquer tipo de pesquisa adequado ao tipo de dados a indexar. Essa estrutura, Generalized Search Tree (GiST), permite
acrescentar, por exemplo, pesquisas multidimensionais sobre dados espaciais, mesmo
que o SGBD não disponha desta funcionalidade. A estrutura GiST permite também definir
os três métodos fundamentais de um índice: pesquisar, inserir e remover. Adicionalmente,
164
© FCA – Editora de Informática
FUNDAMENTOS DE BASES DE DADOS
nes a dependências entre colunas. Por serem a técnica mais utilizada pelos SGBD, vamos
detalhá-los na secção 7.5.
7.5 Histogramas
Na prática, nem os valores dos atributos estão uniformemente distribuídos, nem os atributos são geralmente independentes entre si, embora estas hipóteses permitam calcular
de forma simples a seletividade dos operadores relacionais. Guardar a distribuição completa dos valores de um atributo consumiria muitos recursos e poderia nem sempre trazer
ganhos correspondentes a esse esforço, pelo que os SGBD adotaram estruturas mais
simples e mas eficazes de guardar a distribuição de valores dos atributos: os histogramas.
A primeira proposta de utilização de histogramas para otimização de consultas foi feita por
Kooi (1980).
Um histograma é uma representação com perdas de uma relação. Um histograma de um
atributo de uma dada relação utiliza uma regra para definir B blocos disjuntos onde guardar
a distribuição desse atributo. Uma representação sem perdas registaria a frequência fi para
cada valor vi e teria um tamanho de VDR(A):
{v1, f1}{v2, f2}… {vn, fn}
Dependendo do tamanho de VDR(A), pode não ser praticável manter uma estrutura com
esta distribuição completa. Um histograma não regista todos os valores individualmente,
mas sim grupos de valores reunidos em blocos segundo um determinado critério, como
mostrado na secção 7.5.1. Se o número de blocos for igual ao número de valores, diz-se
que o histograma é completo. De uma forma geral, o número de blocos (ou seja, a sua
largura) define o compromisso entre a ocupação de espaço no catálogo para guardar o
histograma e a precisão pretendida.
A dispersão de um valor é definida como di = vi+1 − vi, d0 = v1 e dn = 1, 1 ≤ i ≤ n. A área de
um valor é definida como ai = fi × di.
Como não se guardam os valores individuais dentro dos blocos, tem de se definir de que
forma estes poderão ser “estimados” quando necessário, para o que se adotam geralmente três premissas:
■■
Premissa de valores contíguos: Assume-se que todos os valores entre os limites
do bloco estão presentes;
■■
Premissa de dispersão uniforme: Guarda-se o número de valores e assume-se que
estão igualmente espaçados dentro do bloco;
■■
Premissa de valor pontual: Assume-se que cada bloco só tem um valor, geralmente o valor mais pequeno dentro do bloco.
A primeira premissa é a mais simples de utilizar, mas introduz erros maiores em distribuições não uniformes. A segunda premissa é geralmente a utilizada. Quanto à frequência,
250
© FCA – Editora de Informática
Otimização de Consultas
7
assume-se que todos os valores de um bloco têm a frequência média do mesmo, sendo
que esta é guardada juntamente com o bloco.
7.5.1Tipos de histogramas mais comuns
Os histogramas podem ser classificados segundo a forma como organizam os blocos. As
formas mais comuns de organização são:
■■
Equilargo: O número de valores em cada bloco (a largura de cada intervalo representado no bloco) é aproximadamente o mesmo; este histograma é também conhecido
por histograma de frequência. Em cada bloco, considera-se que cada valor tem a
frequência média desse bloco;
■■
Equiprofundo: O número de tuplos em cada bloco é aproximadamente o mesmo
e a largura dos blocos é variável. A frequência de cada valor é calculada dividindo a
frequência total da população do bloco pelo número de valores.
Considere-se a distribuição de valores de um dado atributo A, numérico, apresentada na
Tabela 7.3:
Tabela 7.3 – Distribuição de valores de um atributo numérico
2
1
6
8
3
13
12
6
6
3
23
11
16
6
4
2
3
10
0
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Os histogramas unidimensionais (isto é, que representam apenas um atributo), mais comuns são construídos nas secções seguintes.
7.5.1.1Histograma equilargo
A Figura 7.5 mostra um exemplo de um histograma equilargo para a distribuição da Tabela 7.3.
60
40
20
1
16
5
10
15
20
Figura 7.5 – Histograma equilargo
Um histograma consiste em B blocos que são intervalos de valores disjuntos. A largura
de cada um dos B blocos é dada por ⎡(maxR(A) − minR(A))/B⎤. O histograma da Figura 7.5
está organizado em B = 4 blocos, cada um compreendendo 5 valores. Para cada bloco,
mostra-se a contagem dos valores: 20 para o bloco 1,40 para o bloco 2,60 para o bloco
3 e 16 para o bloco 4. A representação do histograma é compacta: cada bloco tem associada uma contagem e, opcionalmente, porque se calculam com facilidade os limites
inferior e superior dos valores que contém. Assim, o bloco 1 compreende os valores
entre 1 e 5, o bloco 2 entre 6 e 10, e assim por diante. Dentro de cada bloco, assume-se
© FCA – Editora de Informática
251
FUNDAMENTOS DE BASES DE DADOS
uma separação uniforme de valores entre os dois limites – basta conhecer o número de
valores dentro do bloco, pois assume-se que estão igualmente espaçados. Repare-se
que se o histograma só tiver um bloco5, reduz-se o cálculo da seletividade aos exemplos
vistos anteriormente.
A construção deste tipo de histogramas é facilitada, se se conhecer os valores mínimo e
máximo do atributo. Se a relação for muito grande, pode contar-se os valores numa amostra aleatória e extrapolar para a relação. Na prática, os SGBD escolhem páginas no disco
e consideram-nas a amostra, o que torna o processo de recolha mais simples e rápido
(dezenas ou centenas de tuplos podem estar na mesma página). No entanto, dependendo
da organização da relação no disco, esta forma de amostragem pode ser enviesada (por
exemplo, se a relação estiver agrupada) e distorcer a construção do histograma. Alguns
SGBD escolhem amostragem por tuplos ou por blocos, dependendo de análise estatística
sobre alguns dados da relação. Chaudhuri, Das e Srivastava (2004) propõem algoritmos de
amostragem por blocos, e utilizam-nos para a estimação de valores distintos.
A manutenção deste tipo de histogramas é simples e consiste em modificar as contagens
dos blocos para cada modificação dos valores na relação.
Exemplo 7.5
A fim de utilizar o histograma para uma seleção do tipo A = 6, usa-se a contagem do bloco
2, com valores entre 6 e 10. O número de tuplos é calculado, assumindo uma distribuição
uniforme de valores dentro do bloco, como sendo 40/5 = 8 (a contagem real é 13). Para uma
seleção do tipo A > 7 ∧ A < 18, temos de considerar parcialmente os blocos 2 (a 3/5) e 4 (a
2/5), e o bloco 3 na totalidade: 40 × 3/5 + 16 × 2/5 + 60 ≈ 90 tuplos (a contagem real é 80).
Se tivéssemos usado o modelo simplificado, o número de tuplos para A = 6 seria 136/20 ≈
7. Para A > 7 ∧ A < 18, teríamos 136 × (18 – 7)/20 ≈ 75 tuplos.
7.5.1.2Histograma equiprofundo
Piatetsky-Shapiro e Connel (1984) propuseram a utilização de um histograma alternativo
ao apresentado, o histograma equiprofundo (ou equifrequência). Este tipo de histograma
guarda um número aproximado (se possível igual), de tuplos em cada bloco, como mostrado na Figura 7.6.
34
34
1
7
34
11 13
34
20
Figura 7.6 – Histograma equiprofundo
A profundidade (ou altura) de cada bloco é dada por |R|/B. Para construir o histograma
ordena-se o atributo A e, começando pelo valor mais baixo, atribui-se a cada bloco aproximadamente o mesmo número de tuplos, neste caso 136/4 = 34. O bloco 1 tem os limites
(1, 7), o bloco 2 (7, 11), o bloco 3 (11, 13) e o bloco 4 (13, 20). Repare-se que o mesmo
5
Diz-se que é um histograma trivial.
252
© FCA – Editora de Informática
Otimização de Consultas
7
valor pode atravessar mais do que um bloco. Os SGBD reconhecem um valor como sendo
“popular”, se este aparecer em mais do que um limite superior de um bloco. Esta técnica
é, no entanto, falível e muito dependente do número de blocos escolhido – na Figura 7.6
nenhum limite superior aparece repetido, embora o 7, o 11 e o 13 sejam valores frequentes. Dentro de cada bloco, assume-se que a frequência de cada valor é uniforme, correspondendo à média das frequências dos valores dentro do bloco.
A obrigatoriedade de ordenação da relação implica geralmente custos elevados para a
construção do histograma, pelo que se pode utilizar, se necessário, uma amostra, com as
precauções já referidas no caso anterior. Note-se que a maioria dos SGBD utiliza amostras
para construir histogramas.
A manutenção deste tipo de histogramas pode implicar fusão e divisão de blocos para
manter, face a modificações na relação, um número de tuplos por bloco o mais equilibrado
possível.
Exemplo 7.6
A fim de utilizar o histograma para uma seleção do tipo A = 6, usa-se a contagem do bloco
1, com valores entre 1 e 7. A contagem estimada é 34/7 ≈ 5 (a contagem real é 13). Para
uma seleção do tipo A > 7 ∧ A < 18, temos de considerar parcialmente o bloco 4 (a 4/7) e os
blocos 2 e 3 na totalidade: 34 + 34 + 34 × 4/7 ≈ 87 (a contagem real é 80).
Os histogramas equiprofundos adaptam-se a enviesamentos na distribuição dos valores,
permitindo que os blocos tenham larguras diferentes. Nestas situações, os histogramas
equilargos podem introduzir erros substanciais nas estimativas.
7.5.2Taxonomia de histogramas
Poosala et al. (1996) propuseram que os histogramas se pudessem classificar segundo os
seguintes parâmetros:
■■
Parâmetro de ordenação: Os autores propuseram que este parâmetro seja o valor
do atributo, a sua frequência ou a área, produzindo valores contínuos, sem sobreposição entre blocos;
■■
Parâmetro de partição: Especifica as restrições no número de elementos de cada
bloco. As classes de partição mais comuns são “série”, que não coloca nenhuma
restrição ao número de elementos, e “end-biased”, que requer que todos os blocos menos um tenham apenas um valor. Estas classes diferem na quantidade de
memória utilizada (maior para a classe “série”) e na precisão (maior para a classe
“end-biased”);
■■
Parâmetro-fonte: Trata-se da propriedade de distribuição dos dados que é mais relevante para a estimação e que é usada juntamente com o parâmetro seguinte para
decidir a partição dos dados. Os parâmetros mais úteis são a dispersão, a frequência
e a área;
© FCA – Editora de Informática
253