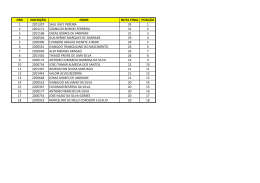
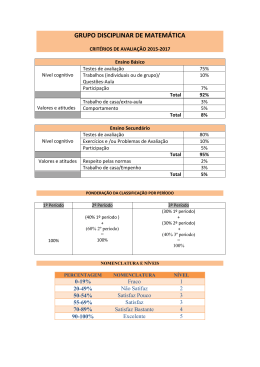
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Um “ efeit o c oligat ivo” é um a
m odific aç ão em c ert as
propriedades de um solvent e
quando nele adic ionados um
s o l u t o n ã o -v o l á t i l , o q u a l s ó
depende do núm ero de
p a r t íc u l a s ( m o l é c u l a s o u ío n s )
dissolvidas e não de sua
n a t u r e za !
n ã o -v o l á t i l : p o n t o d e e b u l i ç ã o s u p e r i o r a o d o s o l v e n t e .
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
As propriedades do solvent e
m odific adas são:
•
Pr e s s ã o d e v a p o r à e f e i t o t o n o m é t r i c o
• Po n t o d e e b u l i ç ã o à e f e i t o e b u l i o m é t r i c o
• Po n t o d e f u s ã o à e f e i t o c r i o m é t r i c o
• Pr e s s ã o o s m ó t i c a à e f e i t o o s m o m é t r i c o
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Ef e i t o T o n o m é t r i c o
Co n s i s t e n a d i m i n u i ç ã o d a p r e s s ã o d e
v a p o r d o s o l v e n t e q u a n d o a d i c i o n a -s e u m
s o l u t o n ã o -v o l á t i l !
Pr e s s ã o d e
vapor é aquela
ex erc ida pelas
m o l é c u l a s (d e
m aior energia) do
solvent e,
c ont ra a
int erfac e para
passar ao
est ado de
vapor.
interface líquido/vapor
Prof . Mat eus Andrade
Pvapor
EFEI T OS COL I GA T I V OS
Co m a a d i ç ã o d e
p a r t íc u l a s d e
s o l u t o (ío n s o u
m oléc ulas)
i n t e n s i f i c a m -s e
as forç as
at rat ivas
m olec ulares e
dim inui a
pressão de vapor
do solvent e.
Um t ec ido úm ido c om água do m ar
dem ora m ais a sec ar do que c om
água da t orneira !
Prof . Mat eus Andrade
Pvapor
Pvapor
soluto
EFEI T OS COL I GA T I V OS
A variaç ão na pressão de vapor pode ser
obt ida do seguint e m odo:
Po = p r e s s ã o d e v a p o r d o s o l v e n t e p u r o
Pv = p r e s s ã o d e v a p o r d o s o l v e n t e , n a s o l u ç ã o
DP = d i m i n u i ç ã o a b s o l u t a d a p r e s s ã o d e v a p o r
DP / P o = d i m i n u i ç ã o r e l a t i v a d a p r e s s ã o d e v a p o r
D P = .C
K
P
v
T
molar
KT = constante tonométrica
Cmolar = concentração molar
o
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Re p r e s e n t a ç ã o g r á f i c a
A p r e ss ã o d e
v a p o r d a so l u ç ã o é
m enor do que a do
s o l ve n t e p u r o .
P ro f. Ma te u s A n d ra d e
EFEI T OS COL I GA T I V OS
Ex e m p l o
Um a soluç ão aquosa de glic ose
a p r e s e n t a c o n c e n t r a ç ã o m o l a r 2 ,0 M .
Sa b e n d o q u e a c o n s t a n t e t o n o m é t r i c a p a r a
a á g u a v a l e 1 ,8 .1 0 -2 , q u a l o a b a i x a m e n t o
relat ivo da pressão de vapor ?
So l u ç ã o
C m o l a r = 2 ,0 m o l /L ; K t
(á g u a )
DP/P o = K t . C m o l a r = 2 ,0
x
= 1 ,8 .1 0 -2
1 ,8 .1 0 -2 = 3 ,6 .1 0 -2
Re s p o s t a : DP/P o = 3 ,6 .1 0 -2
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Ef e i t o Eb u l i o m é t r i c o
Co n s i s t e n o a u m e n t o d a t e m p e r a t u r a d e
e b u l i ç ã o d o s o l v e n t e q u a n d o a d i c i o n a -s e u m
s o l u t o n ã o -v o l á t i l , e x p l i c a d a p e l o a u m e n t o
da int ensidade das forç as int erat ivas, pela
p r e s e n ç a d a s p a r t íc u l a s d o s o l u t o .
To = solvente puro
DTebulição
Prof . Mat eus Andrade
Te = solução
EFEI T OS COL I GA T I V OS
A variaç ão na t em perat ura de ebuliç ão
pode ser obt ida do seguint e m odo:
To = pont o de ebuliç ão do solvent e puro
Te ou T = pont o de ebuliç ão do solvent e, na soluç ão
DT e = a u m e n t o n a t e m p e r a t u r a d e e b u l i ç ã o
DT = K .C
E
E
molar
KE = constante ebuliométrica
Cmolar = concentração molar
A “ água da sopa” ferve a um a t em perat ura
superior àquela da água t orneira !
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Ex e m p l o
Qu a l o a u m e n t o p r o v o c a d o n o p o n t o
de ebuliç ão da água pela dissoluç ão de
3 ,0 m o l s d e g l i c o s e , n u m v o l u m e d e 5 0 0
m L de soluç ão, sendo a c onst ant e
e b u l i o m é t r i c a d a á g u a K e = 0 ,5 2 o C/m o l ?
So l u ç ã o
n 1 = 3 ,0 m o l s ; V = 0 ,5 L ; K e = 0 ,5 2 o C/m o l
DT e = K e . C m o l a r = 0 ,5 2 . 3 ,0 / 0 ,5 = 3 ,1 2 o C
* A s o l u ç ã o i r á f e r v e r n a t e m p e r a t u r a d e 1 0 3 ,1 2 o C.
Re s p o s t a : DT = 3 ,1 2 o C e T e = 1 0 3 ,1 2 o C
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Ef e i t o Cr i o m é t r i c o
Co n s i s t e n a d i m i n u i ç ã o d a t e m p e r a t u r a d e
c ongelam ent o ou fusão do solvent e quando
a d i c i o n a -s e u m s o l u t o n ã o -v o l á t i l .
To = solvente puro
Tf = solução
DTfusão
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
A variaç ão na t em perat ura de
c ongelam ent o ou fusão pode ser obt ida
do seguint e m odo:
To = pont o de fusão do solvent e puro
Tc ou T = pont o de fusão do solvent e, na soluç ão
DT c = d i m i n u i ç ã o n a t e m p e r a t u r a d e f u s ã o
DTC = KC . Cmolar
KE = constante criométrica
Cmolar = concentração molar
A c erveja c ongela a um a t em perat ura
inferior à da água pura !
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Ex e m p l o
Qu a l a d i m i n u i ç ã o p r o v o c a d a n o
pont o de c ongelam ent o da água pela
d i s s o l u ç ã o d e 1 ,5 m o l s d e u r é i a , n u m
volum e de 200 m L de soluç ão, sabendo
que a c onst ant e c riom ét ric a da água vale
K c = 0 ,1 ,8 6 o C/m o l ?
So l u ç ã o
n 1 = 1 ,5 m o l s ; V = 0 ,2 L ; K c = 1 ,8 6 o C/m o l
DT c = K c . C m o l a r = 1 ,8 6 . 1 ,5 / 0 ,2 = 1 3 ,9 5 o C
* A s o l u ç ã o i r á c o n g e l a r n a t e m p e r a t u r a d e – 1 3 ,9 5 o C .
Re s p o s t a : DT = 1 3 ,9 5 o C e T c = - 1 3 ,9 5 o C
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Ef e i t o Os m o m é t r i c o
Co n s i s t e n a m e d i d a d a p r e s s ã o o s m ó t i c a
ent re duas soluç ões separadas ent re sí por
u m a m e m b r a n a s e m i -p e r m e á v e l (m .s .p .) o u
de um a soluç ão c om o solvent e puro.
OB SERV A ÇÕES
A ) M e m b r a n a s e m i -p e r m e á v e l = s ó p e r m i t e a p a s s a g e m d e
s o l v e n t e ( e x .: c i t o p l a s m a , p a p e l c e l o f a n e ,... );
B ) Os m o s e = p a s s a g e m d e s o l v e n t e a t r a v é s d e u m a m .s .p .,
a t é q u e a s s o l u ç õ e s t o r n e m -s e i s o t ô n i c a s , i s t o é , q u e
ex erç am a m esm a pressão osm ót ic a;
C) Pr e s s ã o o s m ó t i c a = p r e s s ã o e x e r c i d a p e l o s o l v e n t e
c o n t r a a m .s .p . p a r a q u e o c o r r a a o s m o s e .
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Pr e s s ã o Os m ó t i c a
soluto
solvente
OSMOSE
d i l u íd a
m esm a c onc ent raç ão
c onc ent rada
APÓS CERTO
TEMPO
m .s .p
m .s .p
Po b r e l e s m a q u a n d o a d i c i o n a m o s s a l !
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
A p r e s s ã o o s m ó t i c a (P) p o d e s e r o b t i d a
do seguint e m odo:
- a pressão ex erc ida por um gás, em dada
t em perat ura, é c alc ulada pela ex pressão
PV=nRT
-p o r a n a l o g i a , a p r e s s ã o o s m ó t i c a s e r á
P V = n RT
nRT mRT
P=
=
= Cmolar RT
V
MV
R = c o n s t a n t e u n i v e r s a l d o s g a s e s (0 ,0 8 2 a t m .L /m o l .K
T = t e m p e r a t u r a a b s o l u t a (K e l v i n )
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Ex e m p l o
Qu a l a p r e s s ã o o s m ó t i c a e x e r c i d a
p o r u m a s o l u ç ã o a q u o s a d e s a c a r o s e 1 ,8
M , n a t e m p e r a t u r a d e 2 7 o C?
• Da d o : R = 0 ,0 8 2 a t m .L / m o l .K
So l u ç ã o
C m o l a r = 1 ,8 ; T = 2 7 o C = 3 0 0 K
P = C m o l a r R T = 1 ,8 x 0 ,0 8 2 x 3 0 0 = 4 4 ,2 8 a t m
Re s p o s t a : P = 4 4 ,2 8 a t m
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Re s u m o d o s e f e i t o s c o l i g a t i v o s
T ON OM ET RI A (P V
D P = .C
K
P
)
v
T
molar
o
EB U L I OM ET RI A (T E
CRI OM ET RI A (T C
OSM OM ET RI A (P)
DT = K .C
)
E
E
molar
DT = K . C
)
C
P=
C
molar
nRT mRT
=
= Cmolar RT
V
MV
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Ef e i t o s c o l i g a t i v o s d e s o l u t o s i ô n i c o s
Em v i r t u d e d o s e f e i t o s c o l i g a t i v o s
d e p e n d e r e m d o n o d e p a r t íc u l a s
p r e s e n t e s e n ã o d a n a t u r e za d a s
m e s m a s ( u m m o l d e ío n s e x e r c e o m e s m o e f e i t o
que um m ol de m oléc ulas) p a r a s o l u t o s
iônic os as ex pressões deverão ser
m ult iplic adas por um fat or de c orreç ão
“ i ” q u e c o r r e p o n d e a o n o d e ío n s
p r o d u zi d o s p o r f ó r m u l a d e s u b s t â n c i a
iônic a.
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Ex e m p l o s :
N a Cl
Ã
N a + + Cl -
i = 2
(2 ío n s )
i = 3
(3 ío n s )
+ 3 Cl -
i = 4
(4 ío n s )
Sn +4 + 4 Cl -
i = 5
(5 ío n s )
A l 2 (SO 4 ) 3 Ã 2 A l +3 + 3 SO 4 -2
i = 5
(5 ío n s )
Ca Cl 2 Ã Ca +2 + 2 Cl Fe Cl 3 Ã Fe +3
Sn Cl 4 Ã
Prof . Mat eus Andrade
EFEI T OS COL I GA T I V OS
Po r t a n t o , a s e x p r e s s õ e s (f ó r m u l a s )
c orrigidas para os efeit os c oligat ivos
iônic os são
Tonom ét ric o
DP = .
K C
P
t
molar
o
Eb u l i o m é t r i c o
.i
DT = K . C
e
c
c
molar
molar
.i
Os m o m é t r i c o
Cr i o m é t r i c o
DT = K . C
e
.i
p =C
Prof . Mat eus Andrade
molar
. R . T .i
EFEI T OS COL I GA T I V OS
Prof . Mat eus Andrade