Aula 16 Modelagem de Transformador Modelagem Iremos apresentar o modelo do transformador para uso no cálculo de fluxo de potência em redes de alta tensão. Estes modelos descrevem matematicamente o comportamento do transformador sob condições estacionárias, com as tensões e correntes variando senoidalmente, ou seja, em regime permanente para a freqüência fundamental do sistema (60 Hz). Para estas condições poderemos representar os transformadores trifásicos por seu equivalente de seqüência positiva. No caso de ligações em delta iremos converter para ligações em estrela equivalentes para podermos trabalhar com a seqüência positiva. Modelagem (cont.) Os transformadores utilizados em sistema de potência (alta tensão) têm algumas características diferentes dos demais. Em geral os efeitos de corrente de magnetização podem ser desprezados (em condições de regime permanente). Os modelos que iremos utilizar serão semelhantes aos modelos Pis utilizados para linhas de transmissão. Iremos rever o sistema pu e aplicaremos o conceito para transformadores. Finalmente apresentaremos as equações de fluxo de potência para os transformadores em condições de regime permanente (representados por seu equivalente de seqüência positiva em pu). Equivalentes de transformador monofásico Dado o transformador monofásico a seguir Podemos representá-lo pelo modelo abaixo. Ip rd + Is j xd + Vp gm j bm Vs - - a:1 Este modelo será utilizado para dedução da expressão de fluxo de potência através do transformador. Modelo teórico No modelo o comportamento elétrico do transformador é representado por um transformador ideal, com relação de transformação a:1. A impedância série representa o fluxo de dispersão (reatância) e a perda no cobre (resistência). A admitância transversal representa a perda de magnetização (susceptância) e as perdas no ferro (Foucault -condutância). Indutâncias Da teoria de transformadores surgem as indutâncias • Lp – indutância própria do primário • Ls – indutância própria do secundário • Mps – indutância mútua primáriosecundário Estas indutâncias são descritas pela permeabilidade magnética do material, um fator que depende da geometria do trafo e um fator de dispersão, além do número de espiras dos enrolamentos primário e secundário. Indutâncias (cont.) Analisando os fasores das tensões no primário e no secundário do transformador pode-se relacionar estas indutâncias com as impedâncias longitudinais e transversais do modelo. Transformador monofásico ideal • Circuito equivalente: • Relações de tensão: dϕ v1 = N1 dt dϕ v2 = N 2 dt V1 N1 = =a V2 N 2 • a – relação de espiras • Relação de corrente: i1 N1 − i2 N 2 = 0 i1 N 2 1 = = i2 N1 a Transformador monofásico ideal • Relações de Potência: S1 = V I = V2 I 2 = S 2 * 1 1 * • Não há perdas (potência de entrada igual a potência de saida) • Relações de impedâncias(reflexão): V1 a V2 2 V2 2 Z1 = = =a = a Z2 I1 I 2 I2 a Transformador monofásico real • Considera-se: •Perdas ôhmicas, resistência dos enrrolamentos do primário e secundário (r1 , r2 ); • Perdas magnéticas por dispersão de fluxo magnético Representadas por Reatâncias lineares (x1 , x2). •Perdas no núcleo – Perdas ativas por Foulcaut e histerese representada por resistência (rc) e a magnetização do núcleo aproximada por reatância linear (aprox. Pela componente de 1ª h da Corrente de magnetização em quadratura com o fluxo) - xm ; • Circuito equivalente: • A relação de espiras é válida para V1’ e V2’ e para I1’ e I2. Transformador 1φ real (em vazio) • EM VAZIO (SECUNDÁRIO EM ABERTO) • I2 = 0 I1’ = 0; • A impedância do ramo de magnetização (rc e xm ) é muito maior que a impedância série equivalente (pode-se desprezar os parâmetros série). • Circuito equivalente: •Corrente no primário (da ordem de 5 % da corrente nominal do trafo): i1 (t ) = iϕ (t ) + im (t ) • Corrente no tensão no secundário: V1 V2 = a Transformador 1φ real (em vazio) • Devido à não linearidades da curva B x H do núcleo (ciclo de histerese e eventualmente saturação): • A corrente de excitação não é senoidal; • A análise de Fourier mostra que a corrente de magnetização possui uma componente fundamental em fase com o fluxo e harmónicas de ordem ímpar (3ª, 5ª, … ) • Como a If é pequena considera-se somente a componente de primeira harmônica: I1 = Iϕ • Diagrama fasorial Transformador 1φ real (com carga) • I2 ≠ 0 Todos os parâmetros do circuito equivalente são considerados; •Podemos eliminar o transformador ideal refletindo as impedâncias do secundário para o primário e utilizando a relação de transformação de tensão e corrente. • Circuito equivalente: • Como Iϕ << I1 pode-se desprezar o ramo de magnetização: • Em geral para trafos de Potência (centenas de kVA), depreza-se as perdas ôhmicas. Ensaios A partir de ensaios é possível determinar os parâmetros do modelo do transformador nas condições de regime permanente : • Curto-circuito – Com o lado de baixa (secundário) em curtocircuito impõe-se uma tensão menor do que a nominal no lado de alta (primário) de modo a se ter corrente nominal no secundário em curto e mede-se a tensão e a corrente no primário, além da corrente no secundário e a potência consumida no primário. • Em Vazio – Com o terminal do lado de alta (secundário) em vazio ompõe-se tensão nominal no lado de baixa (primário) e mede-se a tensão no secundário, além da corrente no primário e a potência consumida no primário. Determinação de parâmetros (Ensaio em vazio) • Teste em aberto: Um dos lados do transformador é deixado em aberto, normalmente o lado de alta tensão. Instrumentos de medição são conectados para medir a corrente I1, V1 e a potência ativa na entrada P1. A tensão aplicada V1 deve ser igual a tensão nominal do transformador (dado de placa). • Como um dos lados em vazio teremos: •I2 = 0 I1’ = 0; • A impedância do ramo de magnetização (rc e xm ) é muito maior que a impedância série equivalente (pode-se desprezar os parâmetros série). • Toda a corrente é responsável pela magnetização do núcleo do trafo. Determinação de parâmetros (Ensaio em vazio) • Como foram desprezadas as perdas ôhmicas no cobre, toda a potência ativa medida representa as perdas ôhmicas no núcleo do tranformador, e desta forma calculamos rc e xm: • Resistência do ramo de magnetização 2 V1 rc1 = P0 • Correntes Ic e Im do ramo de magnetização V1 Ic = rc I m = I1 − I c 2 2 • Reatância de magnetização: V1 X m1 = Im • Nota: Os parâmetros são referentes ao lado de aplicação da tensão V1. Determinação de parâmetros (ensaio em curto) • Ensaio em curto: Um dos lados do transformador é curto-circuitado, normalmente o lado de baixa tensão. Instrumentos de medição são conectados para medir as correntes I2, I1, V2 e potência ativa na entrada P2. A tensão aplicada V2 deve ser tal que I1 seja igual a corrente nominal do transformador (dado de placa). • Com o terminal em curto (situação de plena carga) a tensão aplicada que resulta na corrente nominal é muito menor que a tensão nominal do trafo no lado em que a tensão é aplicada; • Como vimos a corrente de magnétização é de pequena ordem de grandeza, na prática as perdas no ramo de magnetização são desprezadas neste ensaio. Determinação de parâmetros (ensaio em curto) • Desta forma calcula-se o módulo da impedância, Z2 V2 Z2 = I2 • Resistência de perdas no cobre: requiv 2 P2 = 2 I1 • Reatância de dispersão: xequiv 2 = Z 2 − r2 2 2 Exemplos (circuito equivalente) • Testes são feitos em um transformador monofásico, 10 kVA, 2200/220, 60 Hz e anotados na tabela abaixo. Circuito Aberto Curto Circuito Tensão (V) 220 150 Corrente (A) 2,5 4,55 Potência (W) 100 215 • (a)Encontre o circuito equivalente aproximado, com os parametros refletidos de alta e do lado de baixa tensão. •(b)Expressa a corrente de excitação como uma porcentagem da corrente nominal. •(c)Determine o fator de potência para os testes de circuito aberto (sem carga) e curto circuito(plena carga). Solução: Os valores nominais (em módulo) do trafo são descritos abaixo. V2(nominal) = 2200 V a= V1(nominal) = 220 V 2200 = 10 220 I 2(nominal) 10000 10000 = = 4,55 A I1(nominal) = 220 = 45,5 A 2200 V2 I 2(nominal) = V1I1(nominal) = 10 kVA •(a) Parâmetros do Circuito equivalente. •Diagrama fasorial para o teste de circuito aberto. 2 V1 220 2 rc1 = = = 484 Ω P1 100 Ic = V1 220 = = 0,45 A rc 484 I m = I1 − I c = 2,52 − 0,452 = 2,46 A 2 2 V1 220 X m1 = = = 89,4 Ω I m 2,46 •Parâmetros referidos para o lado de alta rc 2 = a 2 rc 2 = 48400 Ω X m 2 = a 2 X m1 = 8940 Ω Solução: •Circuito equivalente e diagrama fasorial para o teste de curto-circuito. P2 215 requiv 2 = 2 = = 10,4 Ω 2 4,55 I1 150 Z2 = = 32,97 Ω 4,55 xequiv 2 = Z 2 − r2 equiv = 32,97 2 − 10,4 2 = 31,3 Ω 2 2 •Parâmetros referidos para o lado de baixa 1 requiv1 = 2 rc 2 = 0,104 Ω a xequiv1 = 1 x = 0,313 Ω 2 equiv 2 a Solução: •(b) Relação porcentual entre corrente de magnetização e nominal. Do teste de circuito aberto, a corrente (magnetização) é de 2,5 A. Portanto: Iϕ I no min al 2,5 %= = 5,5% 45,5 •(c) Fatores de potência •Teste de circuito aberto P 100 fp = = = 0,182 S 2,5 ⋅ 220 •Teste de curto-circuito P 100 fp = = = 0,315 S 4,5 ⋅150 Modelos referidos ao primário e secundário Nos modelos para regime permanente o transformador é representado por um transformador ideal, com sua relação de transformação e a impedância série referida a um dos lados. O ramo da magnetização e as perdas no ferros são desprezados. Modelo referido ao secundário zs Ip Is + + Vs Vp - - a:1 Modelo referido ao primário Ip zp = a2zs Is + + Vs Vp - - a:1 Conexões de transformadores trifásicos Transformadores trifásicos são utilizados para mudar a tensão dos sistemas trifásicos. Normalmente em alta tensão se utiliza bancos de transformadores trifásicos formador por 03 unidades monofásicas. Os enrolamentos primário e secundário podem ser conectados em delta ou estrela, formando bancos ∆- ∆; ∆ Y ; Y ∆ ou Y Y. Os transformadores Y-Y têm um menor custo de isolamento (tensão do enrolamento menor) e permitem acesso ao neutro para aterramento. Para eliminar harmônicas um terceiro conjunto de enrolamento (terciário) é conectado em delta (harmônicas de seqüência zero – 3a harm.). O enrolamento terciário é utilizado para alimentação local e instalação de compensação reativa. Conexões de transformadores trifásicos (cont.) A tensão do enrolamento terciário é normalmente menor (por ex., 500 Y – 230 Y – 69 ∆). A conexão em delta tem que se isolada para tensão de linha (custo maior). As conexões ∆ Y e Y ∆ são bastante freqüentes e são utilizadas como transformadores elevadores junto a usinas e transformadores abaixadores junto a cargas. O neutro do Y normalmente é aterrado. Relação de transformação de transformadores trifásicos Define-se a relação de transformação dos transformadores trifásicos como sendo a relação entre as tensões nominais dos enrolamentos primário e secundário (relação entre o número de espiras). a a' Transformador Zc VenrS VenrP a eq = b VenrP VenrS carga b' Zc c Zc c' Vamos analisar o banco de transformador Y-Y e Y-∆ . Transformador Y-Y ou ∆−∆ Como definimos, a relação de transformação a é definida pela razão entre as tensões dos enrolamentos primário e secundário. a' a b' b Zc Zc Vp carga Vs Zc c' c No caso do banco trifásico com conexão Y-Y (ou ∆−∆) a relação entre as tensões de linha primário/secundário é igual à relação entre as tensões de fase primário/secundário (igual à tensão dos enrolamentos) e não há defasagem entre as tensões dos lados de alta e baixa : a= Vp Vs = Vp φt Vs φt Vp φφ = Vs φφ 3 = 3 Vp φφ Vs φφ Ou seja, para o transformador trifásico Y-Y (ou ∆−∆) a relação de transformação a pode ser obtida da razão entre as tensões nominais de linha ou da razão entre as tensões nominais de fase dos lados primário/secundário. Exercício 1 Um banco de transformador conectado em YY alimenta uma carga de 80 MVA fp 0,85 ind. Representar o conjunto transformador + carga em Ω. N1 N2 carga Diagrama unifilar Dados Transformador 138 kV/13,8 kV Carga S = 80 MVA fp – 0,85 atras. Xdispersão : 15,23 Ω (alta) Potência nominal S = 100 MVA Vnominal 13,8 kV Carga no lado de baixa 2 • − S= V − Z ( ) 2 6 2 Vf 13,8 / 3 .10 13,82 ⇒Z= = = = 2,3805 Ω 6 S1φ 80 (80 / 3).10 Carga vista do lado de alta 2 138 = 238,05 Ω Zalta = 2,3805 × 13,8 Ângulo da impedância θ = cos −1 0,85 = 31,79 ° Reatância de dispersão no lado de baixa 2 13,8 X = 15,23 × = 0,01523 Ω 138 N1 j 15,23 Ω N2 trafo carga 202,34 + j 125,40 Ω Sistema visto do lado de alta N1 j 0,1523 Ω N2 trafo carga 2,0234 + j 1,2540 Ω Sistema visto do lado de baixa Transformador Y-∆ ∆ ou ∆−Y Analisando o transformador trifásico Y-∆ e lembrando que a relação de transformação é dada pela relação entre as tensões dos enrolamentos primário/secundário vemos que : • No lado em Y a tensão do enrolamento corresponde à tensão de fase do sistema, • No lado em ∆ a tensão do enrolamento corresponde à tensão de linha do sistema. a a' b' b Zc Vp Vs Zc carga Zc c c' Desta forma temos : a= Vp φt Vs φφ ou Vp φφ Vs φφ = 3a No caso do banco trifásico com conexão Y-∆ a relação entre as tensões de linha é igual a ◊3 vezes a relação entre as espiras. Lembrando do diagrama fasorial trifásico vemos que um transformador ∆-Y atua como um elemento defasador, por incluir uma defasagem de 30º entre as tensões ∆/Y. ca c −b ab a b bc A relação de transformação passa a ser vetorial, onde a tensão no lado do ∆ está adiantada de 30º em relação a do lado Y. − a= Vp φt Vs φφ .e jπ / 6 Vp φφ = Vs φφ 3 − jπ / 6 .e A relação de transformação pode ser representada como a associação em série de dois elementos, o primeiro com relação de transformação real e o segundo somente com a defasagem. − − aT = ar + ad = Vp φφ ar = 3 Vs φφ − a d = 1.e − jπ / 6 Vp φφ Vs φφ 3 − jπ / 6 .e Normalmente a defasagem é cancelada devido à existência de vários transformadores em cascata. Num sistema radial a defasagem pode ser ignorada a não ser que haja interesse no ângulo das tensões. Com relação ao fluxo de potência no sistema radial não há impacto porque tanto a tensão quanto a corrente sofrem o mesmo defasamento. Em sistemas com malha fechada é preciso verificar se a defasagem precisa ser representada. No Brasil existe uma interligação entre Cemig e Escelsa onde foi instalado um transformador Y-∆ (300 MVA 230/138 kV) para gerar a defasagem devido à restrições de fluxo de potência e esta defasagem deve ser corretamente modelada. Y equivalente Vamos então desprezar a defasagem e lembrar que estamos trabalhando com a representação de seqüência positiva (“uma fase”). Iremos representar a conexão ∆ por um Y equivalente e assim trabalharemos somente com uma fase, supondo que o sistema esteja equilibrado (para que os neutros estejam no mesmo potencial). Quando uma impedância for referida ao lado do ∆ ela deve ser corrigida para o Y equivalente, lembrando que Z∆ ZY = 3 Neste caso a relação de transformação Y-Yeq passa a ser dada pelas relações entre as tensões de linha (como no caso Y-Y). Exercício 2 – Trafo Y-∆ ∆ Represente o transformador conectado em Y∆ por seu equivalente de seqüência positiva. Desprezar a defasagem gerada pelo transformador. N1 N2 Diagrama unifilar Dados Transformador 138 kV/13,8 kV – Y-∆ Xdispersão : 15,23 Ω (alta) Potência nominal S = 100 MVA Reatância de dispersão no lado de baixa 2 13,8 = 0,4569 Ω X = 15,23 × 138 / 3 Trabalhando com Y equivalente Reatância de dispersão no lado de baixa 0,4569 X= = 0,1523 Ω 3 Transformador visto do lado de alta N1 j 15,23 Ω N2 trafo 138 kV Transformador visto do lado de baixa (Y equivalente seq pos) N1 j 0,1523 Ω N2 trafo 13,8 kV Reparem que as impedâncias variam com a relação de entre as tensões de linha. O transformador Y-∆ pode ser substituído por um equivalente Y-Y : N1 N2 138 kV-13,8 kV N1 N2 138 kV-13,8 kV As relações de transformação serão : Vf 1 a= VL 2 a= VL1 VL 2
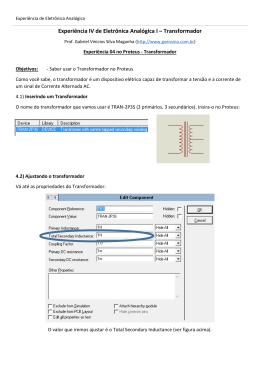
Baixar