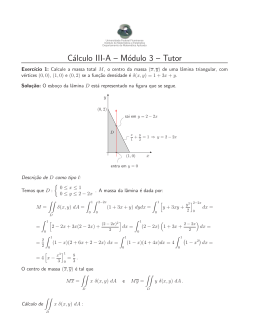
Cálculo de áreas de regiões planas
MAT140 - Cálculo I - Cálculo de áreas de regiões
planas
21 de outubro de 2015
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
UFV
Cálculo de áreas de regiões planas
Teorema
Se f e g são contı́nuas com f (x) ≥ g (x) ao longo de [a, b], então a área
da região entre as curvas y = f (x) e y = g (x) de a ate b é a integral de
(f − g ) de a até b:
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
UFV
Cálculo de áreas de regiões planas
Exemplo
Determine a área da região compreendida entre a parábola y = 2 − x 2 e
a reta y = −x
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
UFV
Cálculo de áreas de regiões planas
Solução
Primeiramente, devemos encontrar os limites de integração.
2 − x2
= −x
x2 − x − 2
=0
(x + 1)(x − 2)
=0
x = −1,
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
x
=2
UFV
Cálculo de áreas de regiões planas
Assim, a região vai de −1 até 2. Os limites de integração são a = −1 e
b = 2. A área A entre as curvas é dada por
Z
b
[(2 − x 2 ) − (−x)]dx
A =
a
Z
2
=
(2 + x − x 2 )dx
−1
= 2x +
x2
2
= (4 +
4
2
=
−
x3
3
i2
−1
− 38 ) − (−2 +
1
2
+ 13 )
9
2
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
UFV
Cálculo de áreas de regiões planas
Exemplo
Determine a área
√ da região do primeiro quadrante que é delimitada
acima por y = x e abaixo pelo eixo x e pela reta y = x − 2.
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
UFV
Cálculo de áreas de regiões planas
Solução
Claramente, a curva y = x −2 intercepta o eixo x no
√ponto (2, 0). Devemos
agora encontrar a interseção entre as curvas y = x e y = x − 2.
√
x =x −2
x
= (x − 2)2
x
= x 2 − 4x + 4
x 2 − 5x + 4
x = 1,
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
x
=0
=4
UFV
Cálculo de áreas de regiões planas
Apenas o valor x = 4 nos interessa, pois x = 1 é uma raı́z que apareceu
√
ao elevarmos o quadrado (graficamente, se traçarmos a curva y = − x
ela iria interceptar a curva y = x − 2 em x = 1)
Para 0 ≤ x ≤ 2; f (x) − g (x) =
Para 2 ≤ x ≤ 4; f (x) − g (x) =
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
√
√
x −0=
√
x
x − (x − 2) =
√
x −x +2
UFV
Cálculo de áreas de regiões planas
Agora, adicionamos as áreas das sub-regiões A e B para determinar a área
total D:
Z
D
=
2√
Z
xdx +
0
=
4√
x − x + 2dx
2
i4
2 3 i2 2 3
x2
x2 + x2 −
+ 2x
3
3
2
0
2
3
3
3
= 32 (2) 2 − 0 + ( 32 (4) 2 − 8 + 8) − ( 23 (2) 2 − 2 + 4)
= 23 (8) − 2 =
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
10
3
UFV
Cálculo de áreas de regiões planas
Exemplo
Ache a área da região limitada pela parábola y 2 = 2x − 2 e pela reta
y = x − 5.
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
UFV
Cálculo de áreas de regiões planas
Solução
Vamos agora, encontrar os pontos onde as curvas se interceptam. Elevando
ao quadrado a curva y = x − 5 e igualando a curva y 2 = 2x − 2, obtemos:
x 2 − 10x + 25
= 2x − 2
x 2 − 12x + 27
=0
(x − 9)(x − 3)
=0
x = 9,
=3
x
Assim, os pontos são (3, −2) e (9, 4).
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
UFV
Cálculo de áreas de regiões planas
A equação y 2 = 2x − 2 equivale as duas equações:
y=
√
√
2x − 2 e y = − 2x − 2.
A primeira, equivale a parte superior da parábola (acima do eixo x) e a
segunda, a metade inferior (abaixo do eixo x). Vamos considerar
√
√
f1 (x) = 2x − 2, f2 (x) = − 2x − 2e g (x) = x − 5.
Agora, iremos encontrar a área da região R1 e R2 , separadas pela reta
x = 3, onde a região R1 é a área delimitada pelas curvas, y = f1 (x),
y = f2 (x) e x = 3, e a região R2 é a área delimitada pelas curvas, y = f1 (x),
y = x − 5 e x = 3.
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
UFV
Cálculo de áreas de regiões planas
Seja A1 e A2 a área das regiões R1 e R2 respectivamente.
Z
A1
3
[f1 (x) − f2 (x)]dx
=
1
Z
=
3
√
√
[ 2x − 2 + 2x − 2]dx
1
Z 3
√
=2
2x − 2dx
1
3
= 23 (2x − 2) 2
=
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
i3
1
16
3
UFV
Cálculo de áreas de regiões planas
Z
A2
9
[f1 (x) − g (x)]dx
=
3
Z
=
3
√
[ 2x − 2 − (x − 5)]dx
1
3
= 13 (2x − 2) 2 − 12 x 2 + 5x
= ( 64
3 −
logo, A1 + A2 =
16
3
+
=
38
3
38
3
= 18.
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
81
2
+ 45) − ( 83 −
i9
3
9
2
+ 15)
UFV
Cálculo de áreas de regiões planas
Exemplo
Ache a área da região limitada pelas curvas y = x 3 − 6x 2 + 8x e
y = x 2 − 4x.
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
UFV
Cálculo de áreas de regiões planas
Solução
Vamos achar os pontos de interseção das curvas:
x 3 − 6x 2 + 8x
= x 2 − 4x
x 3 − 7x 2 + 12x
=0
x(x 2 − 7x + 12)
=0
x(x − 3)(x − 4)
=0
Assim, os pontos de interseção da curva são (0, 0), (3, −3) e (4, 0).
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
UFV
Cálculo de áreas de regiões planas
Seja f (x) = x 3 − 6x 2 + 8x e g (x) = x 2 − 4x.
No intervalo [0, 3], a curva y = f (x) está acima da curva y = g (x), já no
intervalo [3, 4], a curva y = g (x) está acima da curva y = f (x). Dessa
forma, podemos dividir a região entre as curvas, em duas regiões R1 e R2 ,
onde
R1 é a região limitada pelas curvas no intervalo [0, 3] e
R2 é a região limitada pelas curvas no intervalo [3, 4].
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
UFV
Cálculo de áreas de regiões planas
Sejam A1 e A2 a área da região R1 e R2 respectivamente. Logo,
3
Z
[(x 3 − 6x 2 + 8x) − (x 2 − 4x)]dx
A1 + A2 =
0
4
Z
[(x 2 − 4x) − (x 3 − 6x 2 + 8x)]dx
+
3
Z
3
=
(x 3 − 7x 2 + 12x)dx +
0
=
Z
4
(−x 3 + 7x 2 − 12x)dx
3
i3
i4
( 14 x 4 − 73 x 3 + 6x 2 ) + (− 41 x 4 + 73 x 3 − 6x 2 )
0
=
45
7
+
4
12
=
71
6
MAT140 - Cálculo I - Cálculo de áreas de regiões planas
3
UFV