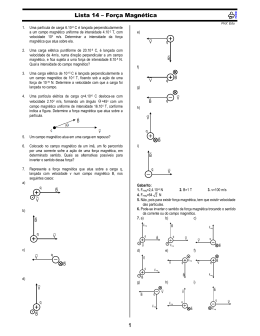
1. Um anel condutor de raio a e resistência R é colocado em um campo magnético
homogêneo no espaço e no tempo. A direção do campo de módulo B é perpendicular à
superfície gerada pelo anel e o sentido está indicado no esquema da figura a seguir.
No intervalo t  1 s , o raio do anel varia de metade de seu valor.
Calcule a intensidade e indique o sentido da corrente induzida no anel. Apresente os cálculos.
2.
Um ciclista pedala sua bicicleta, cujas rodas completam uma volta a cada 0,5 segundo. Em
contato com a lateral do pneu dianteiro da bicicleta, está o eixo de um dínamo que alimenta
uma lâmpada, conforme a figura acima. Os raios da roda dianteira da bicicleta e do eixo do
dínamo são, respectivamente, R = 50 cm e r = 0,8 cm. Determine
a) os módulos das velocidades angulares ωR da roda dianteira da bicicleta e ωD do eixo do
dínamo, em rad/s;
b) o tempo T que o eixo do dínamo leva para completar uma volta;
c) a força eletromotriz E que alimenta a lâmpada quando ela está operando em sua potência
máxima.
NOTE E ADOTE
π 33
O filamento da lâmpada tem resistência elétrica de 6  quando ela está operando em sua
potência máxima de 24 W.
Considere que o contato do eixo do dínamo com o pneu se dá em R = 50 cm.
3. Uma mola de massa desprezível presa ao teto de uma sala, tem sua outra extremidade
atada ao centro de uma barra metálica homogênea e na horizontal, com 50 cm de comprimento
e 500 g de massa. A barra metálica, que pode movimentar-se num plano vertical, apresenta
resistência ôhmica de 5  e está ligada por fios condutores de massas desprezíveis a um
gerador G de corrente contínua, de resistência ôhmica interna de 5  , apoiado sobre uma
mesa horizontal. O sistema barra-mola está em um plano perpendicular a um campo magnético

B horizontal, cujas linhas de campo penetram nesse plano, conforme mostra a figura.
Determine:
a) a força eletromotriz, em volts, produzida pelo gerador e a potência elétrica dissipada pela
barra metálica, em watts.
b) a deformação, em metros, sofrida pela mola para manter o sistema barra-mola em equilíbrio
mecânico. Suponha que os fios elétricos não fiquem sujeitos a tensão mecânica, isto é,
esticados.
4. Um bloco rígido e isolante de massa 400 g possui uma carga elétrica embutida positiva de
10,0 C e encontra-se em repouso em uma superfície definida pelo plano zy no ponto A, como é

representado na figura a seguir. Um campo elétrico uniforme e constante E, de intensidade
1,00 x 102 N/C, é mantido ligado acelerando linearmente o bloco, até este atingir o ponto B. No

trecho entre os pontos B e C, um campo magnético uniforme e constante B é aplicado
perpendicularmente ao plano xy representado por esta folha de papel e com sentido para
dentro do papel. Considere que o bloco pode deslizar livremente, sem atrito, entre os pontos A
e C; porém, existe atrito entre os pontos C e D.
a) Determine a velocidade escalar do bloco no momento imediatamente antes de atingir o
ponto B. Considere que o bloco é um ponto material e que a distância entre A e B é de 50,0
cm.
b) Identifique e desenhe, num diagrama, as forças que atuam no bloco, quando ele se encontra
entre os pontos B e C.
c) Encontre a intensidade do campo magnético para que a força de contato entre o bloco e a
superfície definida pelo plano zy seja nula no trecho de B a C.
d) Determine o coeficiente de atrito cinético entre o bloco e a superfície definida pelo plano zy
em função de v, g e d, considerando que o bloco chega ao ponto C com uma velocidade
horizontal v e para no ponto D, percorrendo uma distância d.
5. A tabela a seguir apresenta algumas propriedades dos fios de cobre comumente utilizados
em circuitos e instalações elétricas.
Considerando que a resistividade do cobre a 20 °C é igual a 1,7 × 10-8 Ω m, e as informações
fornecidas na tabela acima, resolva as questões a seguir:
a) Calcule a resistência por unidade de comprimento de um fio de cobre de calibre 12.
b) Para a montagem de um circuito elétrico são necessários 10 m de fio de cobre. A resistência
máxima oferecida pelo fio não poderá ser maior do que 2,0 x 10-2 Ω para o bom funcionamento
do circuito. Determine qual o diâmetro mínimo de fio que pode ser utilizado para a montagem
do circuito e identifique qual o calibre do fio.
c) Determine o campo magnético a 10 cm de um fio (longo e reto) de cobre de calibre 20,
quando nele estiver passando uma corrente elétrica contínua igual a 2,0 A.e
6. Para estimar a intensidade de um campo magnético B0, uniforme e horizontal, é utilizado
um fio condutor rígido, dobrado com a forma e dimensões indicadas na figura, apoiado sobre
suportes fixos, podendo girar livremente em torno do eixo OO'. Esse arranjo funciona como
uma "balança para forças eletromagnéticas". O fio é ligado a um gerador, ajustado para que a
corrente contínua fornecida seja sempre i = 2,0 A, sendo que duas pequenas chaves, A e C,
quando acionadas, estabelecem diferentes percursos para a corrente. Inicialmente, com o
gerador desligado, o fio permanece em equilíbrio na posição horizontal. Quando o gerador é
ligado, com a chave A, aberta e C, fechada, é necessário pendurar uma pequena massa M1 =
0,008 kg, no meio do segmento P3 - P4, para restabelecer o equilíbrio e manter o fio na posição
horizontal.
a) Determine a intensidade da força eletromagnética F1, em newtons, que age sobre o
segmento P3P4 do fio, quando o gerador é ligado com a chave A, aberta e C, fechada.
b) Estime a intensidade do campo magnético B0, em teslas.
c) Estime a massa M2, em kg, necessária para equilibrar novamente o fio na horizontal, quando
a chave A está fechada e C, aberta. Indique onde deve ser colocada essa massa, levando em
conta que a massa M1 foi retirada.
NOTE E ADOTE:
F = iBL
Desconsidere o campo magnético da Terra.
As extremidades P1, P2, P3 e P4 estão sempre no mesmo plano.
7. Um longo solenoide de comprimento L, raio a e com n espiras por unidade de comprimento,
possui ao seu redor um anel de resistência R. O solenoide está ligado a uma fonte de corrente
I, de acordo com a figura. Se a fonte variar conforme mostra o gráfico, calcule a expressão da
corrente que flui pelo anel durante esse mesmo intervalo de tempo e apresente esse resultado
em um novo gráfico.
8. Parte de uma espira condutora está imersa em um campo magnético constante e uniforme,
perpendicular ao plano que a contém. Uma das extremidades de uma mola de constante
elástica k  2,5 N / m está presa a um apoio externo isolado e a outra a um lado dessa espira,
que mede 10 cm de comprimento.
Inicialmente não há corrente na espira e a mola não está distendida nem comprimida. Quando
uma corrente elétrica de intensidade i = 0,50 A percorre a espira, no sentido horário, ela se
move e desloca de 1,0 cm a extremidade móvel da mola para a direita. Determine o módulo e o
sentido do campo magnético.
9. Na figura, uma placa quadrada de lado L = 2,0 cm, de material condutor, é percorrida por
uma corrente elétrica no sentido y crescente. Ao aplicarmos um campo magnético constante de
módulo B = 0,80 T, os portadores de carga em movimento, que originam a corrente de
intensidade i, são deslocados provocando um acúmulo de cargas positivas na borda de trás e
negativas na da frente, até que a diferença de potencial entre essas bordas se estabilize com
valor ΔV  4,0.107 V , o que resulta em um campo elétrico uniforme na direção x, decorrente
dessa separação de cargas, que compensa o efeito defletor do campo magnético. Esse
fenômeno é conhecido como efeito Hall.

Determine o módulo do vetor campo elétrico E , gera do na direção x, e o módulo da média
das velocidades dos portadores de carga na direção y.
Gabarito:
Resposta da questão 1:
ΔΦ
Lei de Faraday: ε  
; onde:
Δt
ε = tensão elétrica.
Δt = 1s.
ΔΦ  Φ  Φ0  B.S  B.S0  B.(S  S0 )
Como S  π.a2 (área do círculo), teremos:
a
3
ΔΦ  B.( π.( )2  π.a2 )   .B.π.a2
2
4
Substituindo na lei de Faraday:
3
 .B.π.a2
ΔΦ
ε
 4
Δt
1
3
ε  .B.π.a2
4
De acordo com a definição de resistência elétrica: R 
ε
; concluímos:
i
3
.B.π.a2
ε
ε
4
R  i i
i
R
R
i
3.B.π.a2
(com unidades no S.I.), no sentido horário.
4.R
Nota: o sentido foi determinado pela "regra da mão direita".
Resposta da questão 2:
a) Dado: π  3 ; TR = 0,5 s; R = 50 cm; r = 0,8 cm.
2π 2  3
ωR 

 ωR  12 rad / s.
TR
0,5
Como não há escorregamento relativo entre a roda e o eixo do dínamo, ambos têm mesma
velocidade linear. Então:
ωR R 12  50 
vD  vR  ωD r  ωR R  ωD 

 ωD  750 rad / s.
r
0,8
b) Usando novamente a expressão que relaciona o período de rotação e a velocidade angular:
2π
2π 2  3
ωD 
 T

 T  8  103 s.
T
ωD 750
c) Dados: P = 24 W; R  6Ω .
P
ε2
R
 24 
ε2
6
 ε2  144  ε  12 V.
Resposta da questão 3:
Dados:
R  5; r  5; m  500g  0,5kg; L  50cm  0,5m; i  5A; B  0,4T; k  80N / m; g  10m / s2
a) Aplicando a lei de Ohm-Pouillet para o circuito:
  R  r  i     5  5  5    50 V.
A potência elétrica dissipada é:
2
Pot  R i2  5  5 
 Pot  125 W.
b) Pela Regra da mão direita, concluímos que a força magnética na barra é vertical e para cima
e tem intensidade:
Fmag  BiL sen90º  0,4 5 0,5   1 N.
O peso da barra é:
P  mg  0,5 10   P  5 N.
Como o peso tem intensidade maior que a da força magnética, a mola está distendida, isto
é, a força elástica Fel  é para cima, conforme indicado no esquema:
Do equilíbrio:
Fel  Fmag  P  80x  1  5  x 
4
 0,05 m  x  5 cm.
80
Resposta da questão 4:
Dados: m = 400 g = 0,4 kg; q = 10 C; E = 102 N/C; dAB = 50 cm = 0,5 m.
a) Usando o Teorema da Energia Cinética no percurso AB:

τ A,B
F
vB 
2
m v2
m vB
A


2
2
 
2 10  102  0,5 
0,4
vB  50 m / s.
 q E dAB 
2
m vB
2

vB 
2 q E dAB
m

 2.500 

b) No trecho BC, agem no bloco: o peso P , a força magnética, que, pela regra da mão


direita, tem sentido vertical para cima, F e a força normal N , caso a força magnética
 
 
 
seja menos intensa que o peso. O diagrama ilustra a situação.
c) Para que a normal se anule e o bloco não saia do plano horizontal no trecho BC, a força
peso e a força magnética devem ter a mesma intensidade. A velocidade nesse trecho é mesma
com que o bloco atinge o ponto B, ou seja: v = 50 m/s.
FP  q v Bm g  B
m g 0,4 10 

q B 10  50 

B  8  103 T.
d) Nesse trecho CD, a única força realizando trabalho é a componente de atrito. Assim,
aplicando novamente o Teorema da Energia Cinética:

τC,D

Fat
μ
2
2
m vC
m vD

2
2
 μ m g dcos180  0 
m v2
2
 μ m g d  
m v2
2

v2
.
2 gd
Resposta da questão 5:
R = .L/A  R/L = /A = 1,7.10-8 / (3,5.10-6) = 0,486.10-2 = 4,86.10-3/m
R = .L/A  2.10-2 = 1,7,10-8.10/A  A = 8,5.10-6 m2 = 8,5 mm2. Esta é a área transversal
do fio para que a resistência seja de exatamente 2.10-2 . Como a resistência e a área são
inversamente proporcionais, para se ter a máxima resistência a área deve ser de no mínimo
8,5 mm2. O calibre 12 é o indicado. O diâmetro associado a esta área será o diâmetro mínimo
 A = .r2 = .d2/4  d2 = 4.A/ = 4.8,5/3,14 = 10,83  d = 3,29 mm
B = 0.i/(2r)
 B = 4..10-7.2 / (2..0,1) = 4.10-6 T
Resposta da questão 6:
A força magnética equilibra a força peso então F1 = P1 = M1.g = 0,008.10 = 0,08 N
Sabemos que F = i.B.L
 0,08 = 2.B.0,2  B = 0,2 T
Com a inversão das chaves, sem a ação de outra força que não a magnética, ocorrerá a
formação de um binário de forças de módulo 0,08 N. Para neutralizar o binário a força peso da
massa M2 deverá ter o torque de mesmo módulo, mas sentido oposto. Posicionando a ação da
massa no ponto médio do segmento P3P4 a massa M2 deverá ser o dobro de M1 e logo M2 =
2.0,008 = 0,016 kg. A figura a seguir mostra a situação final.
Resposta da questão 7:
Resolução
O campo magnético no interior do solenoide é dado por:
B=
N
.1.N
, em que
=n
L
L
B=µ.I.n
O fluxo magnético Ф é:
Ф = B . A = µ . I . n . πa2
Pela Lei de Faraday:
E=-

t
 I 

 t 
E = – µ . n . πa2 
A corrente induzida no anel é:
E
.n..a2  I 
i
i=
 t 
R
R
 
Seja k = µ . n . π . a2 (constante)
i=
k  I 
R  t 
Pela análise do gráfico:
1º trecho: 0 ≤ t ≤ 1s
I 2A
A

2
t 1s
s
2º trecho: 1s ≤ t ≤ 2s
i2 = 0 pois o fluxo não varia
3º trecho: 2s ≤ t ≤ 4s
I
A
k
 1  i3 
t
s
R
Gráfico da corrente induzida (i) em função do tempo (t):
Resposta da questão 8:
Se a mola sofre distensão, a força magnética tem sentido para a direita. Aplicando a regra da
mão direita, conclui-se que o vetor indução magnética é perpendicular ao plano da página, dela
saindo, como indica a figura.
i
Interbits®
Fmag
Na posição de equilíbrio a forma magnética tem a mesma intensidade da força elástica.
Dados: i  0,5 A; x  1 cm  10–2 m; k  2,5 N / m; L  10 cm  10 –1m.
Fmag  Felast

B i L k x

B
k x 2,5  102

 5  10 1 
i L 0,5  101
B  0,5 T.
Resposta da questão 9:
Dados: ΔV  4  10–7 V; L  2 cm  2  10–2 m.
E L  V

E
V 4  107

L
2  102

E  2  105 V / m.
Quando atinge essa compensação, a força magnética e a força elétrica atingem a mesma
intensidade. Assim:
Fmag  Felet

| q | v B | q | E
v  2,5  105 m / s.

v
E 2  105

B
0,8
