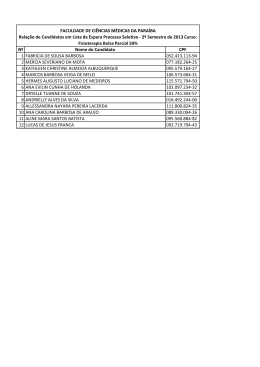
Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Estatística para dados direccionais Susana Barbosa Mestrado em Ciências Geofísicas 2012-2013 Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Dados direccionais observações de direcções no plano ou no espaço 2-D (plano): dados circulares 3-D (espaço): dados esféricos Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Estatística circular Estatística circular métodos estatísticos para análise de dados circulares “A curious byway of statistics. . . somewhere between the analysis of linear and the analysis of spherical data” (Fisher 1993) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Dados circulares I direcção representada por um ângulo medido em relação a uma direcção “zero” arbitrária I não há uma ordenação natural das observações I 0 = 2π (o início e o fim coincidem) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Dados circulares em geofísica Medidas I vento I ondulação I ... Aplicações I produção de energia renovável I riscos, protecção costeira I ... Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo Direcção tomada por 76 tartarugas após serem libertadas (Stephens, 1969) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo Direcção tomada por 76 tartarugas após serem libertadas (Stephens, 1969) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo Direcção tomada por 76 tartarugas após serem libertadas (Stephens, 1969) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo Direcção do eixo maior de 164 formas de feldspato em basalto (Fisher, 1993) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Representação de dados circulares (x = r cos α, y = r sin α) ⇐⇒ (r , α) r = 1 (na estatística circular o interesse é apenas na direcção) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Direcção média A direcção média (direcção preferencial) não deve ser calculada a partir da média dos ângulos! Exemplo: (45 + 90 + 135)/3 = 90 (0 + 45 + 315)/3 = 120 Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Direcção média O valor da média angular depende I origem (arbitrária) I sentido (horario, anti-horario) =⇒ é necessária uma medida alternativa da média para dados direccionais =⇒ como a variância depende da média, é também necessária uma medida alternativa de dispersão para dados direccionais Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Direcção média n observações (xi , yi ) ⇔ (cos αi , sin αi ), i = 1, ..., n P P Vector resultante: R = ( ni=1 cos αi , ni=1 sin αi ) ≡ (C, S) A média circular ᾱ0 é definida como ᾱ0 = arctg(S/C)) Nota: quando R = 0 não existe uma direcção média (observações distribuídas uniformemente sobre o círculo, não há uma direcção preferencial) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Dispersão circular A variância circular é definida como S =1− 1 n Pn i=1 cos(αi − ᾱ0 ) = 1 − ||R||/n P P onde R é o vector resultante R = ( ni=1 cos αi , ni=1 sin αi ) N: 0 < S < 1 S ∼ 0 observações com a mesma direcção S ∼ 1 observações dispersas pela circunferência unitária Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Distribuição de probabilidade circular Distribuição circular: distribuição de probabilidade para variáveis angulares em que toda a probabilidade está concentrada na circunferência do ciclo unitário A função densidade de probabilidade circular f (θ) verifica f (θ) ≥ 0 ´ 2π 0 f (θ)dθ = 1 f (θ) = f (θ + k 2π) ∀k Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Distribuição uniforme A função densidade de probabilidade da distribuição circular uniforme é f (θ) = 1 2π , θ ∈ [0, 2π) (todas as direcções têm igual probabilidade) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Distribuição de von Mises A fdp da distribuição de von Mises é f (θ) = 1 2πI0 (k ) exp[kcos(θ − µ)], θ ∈ [0, 2π), k > 0 onde I0 (k ) é uma função de Bessel modificada de ordem 0, ´ 2π 1 I0 (k ) = 2π 0 exp[k cosθdθ] (“distribuição normal circular” - distribuição mais comum para dados circulares simétricos e unimodais) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Distribuição de von Mises µ- direcção média a distribuição de von Mises tem o valor máximo para θ = µ a distribuição é simétrica em torno de µ k - parâmetro de dispersão k → 0 distribuição von Mises → distribuição uniforme k → ∞ distribuição concentrada na direcção de µ Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Testes de hipótese para dados circulares I Testes de Uniformidade I Testes de Homogeneidade Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Testes de uniformidade Distribuição uniforme f (θ) = 1 2π , θ ∈ [0, 2π) (todas as direcções têm igual probabilidade) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Teste de Rayleigh Assumindo que a distribuição dos dados é de Von Mises com parâmetro de dispersão k H0 : k = 0 H1 : k > 0 (distribuição unimodal com direcção média desconhecida) H 1 : k > 0 & µ = µ0 (distribuição unimodal com direcção média µ0 ) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo H0 : k = 0 H1 : k > 0 P-value: 0.15 H0 : k = 0 H1 : k > 0 & µ = π P-value: Susana Barbosa: Análise de dados em Geociências 0.96 Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo H0 : k = 0 H1 : k > 0 P-value: 0 H0 : k = 0 H1 : k > 0 & µ = π P-value: Susana Barbosa: Análise de dados em Geociências 0 Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Teste de Kuiper Teste não-paramétrico de uniformidade H0 : a distribuição dos dados é uniforme (todas as direcções têm igual probabilidade) P-value > 0.15 Susana Barbosa: Análise de dados em Geociências P-value:< 0.01 Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Outros testes de uniformidade não-paramétricos I Teste de Watson I Teste de espaçamento de Rao I Teste de Ajne I ... Vantagens dos testes não-paramétricos - amostras pequenas - dados não-unimodais Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Testes de homogeneidade Para duas amostras de dados circulares I a direcção média (direcção preferencial) das duas populações é a mesma? I a variância circular (dispersão) é igual? Em ambos os casos assume-se que os dados são amostras de populações com distribuição de von Mises Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Teste de Watson H 0 : µ1 = µ2 P-value Susana Barbosa: Análise de dados em Geociências < 0.05 Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Teste de Watson H 0 : µ1 = µ2 P-value Susana Barbosa: Análise de dados em Geociências < 0.05 Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Teste de Rao H 0 : k1 = k2 P-value Susana Barbosa: Análise de dados em Geociências > 0.1 Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Teste de Rao H 0 : k1 = k2 P-value Susana Barbosa: Análise de dados em Geociências < 0.01 Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Intervalos de confiança - exemplo Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Intervalos de confiança - exemplo mle.vonmises(x) mu: 2.974 ( 0.1080 ) kappa: 2.308 ( 0.3966 ) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Intervalos de confiança - exemplo Bootstrap Confidence Intervals Confidence Level: 95 % Mean Direction: Low = 2.7 High = 3.2 Concentration Parameter: Low = 1.8 High = 3.1 Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Correlação circular O coeficiente de correlação circular para dois conjuntos de dados circulares (αi , βi ), i = 1, ..., n com direcção média µ e ν (em relação à mesma direcção inicial e com o mesmo sentido de rotação) é dado por ρc = E[cos(α − β − µ + ν) − cos(α + β − µ − ν)] p 2 E[sin2 (α − µ)]E[sin2 (β − ν)] Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Correlação circular Propriedades do coeficiente de correlação circular I ρc (α, β) = ρc (β, α) I |ρc (α, β)| ≤ 1 I ρc = 0 se α e β são independentes (o inverso não é verdadeiro) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Correlação circular O coeficiente de correlação circular amostral para duas amostras (αi , βi ), i = 1, ..., n com direcção média ᾱ e β̄ é dado por Pn sin(αi − ᾱ)sin(βi − β̄) rc = qPi=1 n 2 2 i=1 sin (αi − ᾱ)sin (βi − β̄) Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo rc = 0.90 P-value < 0.01 Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Exemplo rc = 0.21 P-value = 0.07 Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013 Introdução Medidas descritivas Distribuições de probabilidade circulares Testes de hipótese Referências Batschelet, E. (1981). Circular Statistics in Biology, Academic Press Jammalamadaka, S.R. & Sengupta, A. (2001). Topics in Circular Statistics. World Scientific, River Edge, N.J. Susana Barbosa: Análise de dados em Geociências Mestrado em Ciências Geofísicas 2012-2013
Download