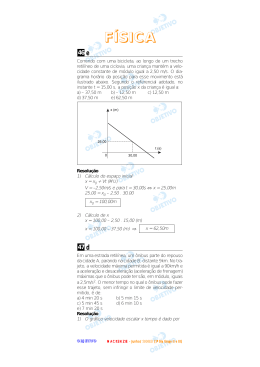
alternativa D
Questão 46
Correndo com uma bicicleta, ao longo de um
trecho retilíneo de uma ciclovia, uma criança
mantém a velocidade constante de módulo
igual a 2,50 m/s. O diagrama horário da posição para esse movimento está ilustrado a seguir. Segundo o referencial adotado, no instante t = 15,00 s , a posição x da criança é
igual a:
a) −37,50 m
d) 37,50 m
b) −12,50 m
e) 62,50 m
c) 12,50 m
alternativa E
O movimento é uniforme e retrógrado de velocidade escalar v = −2,50 m/s. Portanto, temos:
x − x1
∆x
v =
= 2
⇒
∆t
t 2 − t1
⇒ −2,50 =
25,00 − x1
⇒
30,00 − 15,00
x = 62,50 m
Questão 47
Em uma estrada retilínea, um ônibus parte
do repouso da cidade A, parando na cidade B,
distante 9 km. No trajeto, a velocidade máxima permitida é igual a 90 km/h e a aceleração e desaceleração (aceleração de frenagem)
máximas que o ônibus pode ter são, em módulo, iguais a 2,5 m/s2 . O menor tempo no
qual o ônibus pode fazer esse trajeto, sem infringir o limite de velocidade permitido, é de:
a) 4 min 20 s
b) 5 min 15 s
c) 5 min 45 s
d) 6 min 10 s
e) 7 min 20 s
O tempo (t’) que o ônibus leva para atingir a velocidade máxima permitida v = 90 km/h = 25 m/s é
dado por:
0
v − v0
∆v
a=
⇒ a=
⇒
∆t
t’ − t0 0
⇒ 2,5 =
25
⇒ t’ = 10 s
t’
Após atingir a velocidade máxima, o ônibus a
manterá até 10 s antes de parar, pois as acelerações inicial e final do movimento são iguais
em módulo. Assim o gráfico de v versus t é
dado por:
Sendo a área sob o gráfico v versus t numericamente igual ao deslocamento ∆S = 9 000 m, temos:
[t + (t − 20)] ⋅ 25
9 000 =
⇒ t = 370 s ⇒
2
⇒ t = 6min10s
Questão 48
Um operário da construção civil necessita
arrastar um bloco de concreto ao longo de
uma prancha inclinada de 30o com a horizontal. Com o objetivo de evitar o rompimento
da corda, o mesmo foi orientado a puxar o
corpo com velocidade constante, de forma
que se deslocasse 1,00 m a cada 4,0 s. Seguindo essas orientações, sabia-se que a intensidade da força tensora no fio corresponderia a 57% do módulo do peso do corpo.
Considerando a corda e a polia como sendo
ideais, o coeficiente de atrito dinâmico entre
as superfícies em contato, nesse deslocamento, é aproximadamente:
física 2
Dados:
sen 30o = cos 60o = 0,50
sen 60o = cos 30o = 0,87
sen 45o = cos 45o = 0,71
a) 4,0 km/h
d) 16,0 km/h
b) 8,0 km/h
e) 32,0 km/h
c) 14,4 km/h
alternativa C
Como o percentual de perda de energia mecânica
é constante (considerando, obrigatoriamente, o
plano horizontal de referência na base da rampa),
o percentual de energia mecânica que se conserva também é constante.
Assim, temos:
C’
C
Em
Em
=
⇒
A
B
Em
Em
a) 0,87
d) 0,25
b) 0,80
e) 0,08
c) 0,57
mg ⋅ 3,20
⇒
=
mg ⋅ 4,00
alternativa E
As forças que atuam sobre o bloco são dadas
por:
⇒ 0,8 =
⇒
32 +
mv 2
2
mg ⋅ 5,00
mg ⋅ 3,20 +
v2
2
50
⇒
⇒ v = 4 m/s ⇒
v = 14,4 km/h
Obs.: como a questão fornece uma relação percentual, teríamos outra resposta se tomássemos
outro plano horizontal de referência que não o da
base da rampa.
Como a velocidade é constante, temos:
R = 0 ⇒ 0,57P = P sen 30 o + fat . ⇒
⇒ 0,57P = P sen 30 o + µ ⋅ N ⇒
⇒ 0,57P = P ⋅ 0,50 + µ ⋅ P cos 30 o ⇒
⇒ 0,57 = 0,50 + µ ⋅ 0,87 ⇒
⇒ µ = 0,08
Questão 49
Um garoto, que se encontra apoiado sobre
seu “skate”, desce por uma rampa, saindo do
repouso no ponto B. Deslocando-se sempre
sobre o mesmo plano vertical, atinge o ponto
C, com velocidade nula. Admitindo o mesmo
percentual de perda de energia mecânica, se
o garoto saísse do repouso no ponto A, atingiria o ponto C com velocidade:
Questão 50
O tipo de luminária ilustrada a seguir foi utilizado na decoração de um ambiente. A haste
AC, presa à parede, é homogênea, tem secção
transversal constante e massa 800 g. Quando
o lampadário, pendente em A, tem massa superior a 500 g, o fio ideal AB arrebenta. Nesse caso, podemos dizer que a intensidade máxima da força tensora suportada por esse fio
é:
Dado: g = 10 m/s2
Dado: g = 10 m/s2
a) 15 N
d) 8 N
b) 13 N
e) 5 N
c) 10 N
física 3
alternativa A
Marcando as forças sobre a barra, na iminência
do rompimento do fio, temos:
Estando a barra em equilíbrio e adotando o momento positivo no sentido horário, vem:
M R (C) = 0 ⇒ P ⋅ 20 + Pl ⋅ 40 − T ⋅ senα ⋅ 40 = 0 ⇒
30
⇒ 0,8 ⋅ 10 ⋅ 20 + 0,5 ⋅ 10 ⋅ 40 − T ⋅
⋅ 40 = 0 ⇒
50
⇒ T = 15 N
Questão 51
Em uma história de ficção científica, um astronauta, ao descer no planeta Argus, de diâmetro igual a 1/4 do diâmetro da Terra, verifica que o módulo de seu peso é o dobro do
que seria na Terra. Lembrando a Lei da Gramm
vitação Universal de Newton, F = G 1 2 2 ,
d
concluímos que a massa do planeta Argus é:
a) metade da massa da Terra.
b) um quarto da massa da Terra.
c) um oitavo da massa da Terra.
d) o dobro da massa da Terra.
e) o quádruplo da massa da Terra.
alternativa C
Do enunciado, temos:
G ⋅ mA ⋅ m
2 G ⋅ mT ⋅ m
=
⇒
PA = 2 PT ⇒
2
dA
dT2
4
4
⇒
mA
 dT 


 4 
2
⇒ mA =
= 2
1
m
8 T
mT
dT2
⇒
m A ⋅ 16
dT2
=
2 mT
dT2
⇒
Questão 52
Um espelho esférico côncavo, que obedece às
condições de Gauss, fornece, de um objeto colocado a 2 cm de seu vértice, uma imagem
virtual situada a 4 cm do mesmo. Se utilizarmos esse espelho como refletor do farol
de um carro, no qual os raios luminosos refletidos são paralelos, a distância entre o filamento da lâmpada e o vértice do espelho
deve ser igual a:
a) 2 cm
b) 4 cm
c) 6 cm
d) 8 cm
e) 10 cm
alternativa B
Para que os raios emergentes sejam paralelos o
filamento da lâmpada deve ser colocado sobre o
foco do espelho. Assim, da Equação de Gauss,
temos:
1
1
1
1
1
1
=
+
⇒
=
+
⇒ f = 4 cm
f
p
p’
f
2
( −4)
Questão 53
Um corpo C, de massa 1,00 ⋅ 10−1 kg, está
preso a uma mola helicoidal de massa desprezível e que obedece à Lei de Hooke. Num
determinado instante, o conjunto se encontra em repouso, conforme ilustra a figura 1,
quando então é abandonado e, sem atrito, o
corpo passa a oscilar periodicamente em torno do ponto O. No mesmo intervalo de tempo
em que esse corpo vai de A até B, o pêndulo
simples ilustrado na figura 2 realiza uma oscilação completa.
física 4
alternativa E
Da relação entre a escala Celsius e a escala
Fahrenheit temos:
∆θC
∆θF
∆θC
3,6
=
⇒
=
⇒ ∆θC = 2 oC
5
9
5
9
A proporção entre o comprimento da coluna e a
variação da temperatura é dada por:
Sendo g = 10 m/s2 , a constante elástica da
mola é:
a) 0,25 N/m
b) 0,50 N/m
c) 1,0 N/m
d) 2,0 N/m
e) 4,0 N/m
alternativa B
Do enunciado, enquanto o sistema massa-mola
realiza meia oscilação, o pêndulo simples realiza
uma oscilação completa. Portanto, o período T de
oscilação do primeiro é o dobro do período T’ de
oscilação do segundo. Assim, temos:
m
T = 2π
k
T’ = 2 π
l
g
⇒ 2π
m
l
= 2 ⋅ 2π
⇒
k
g
T = 2T’
x (cm)
∆θC ( oC)
2,7
x
3,6
2
⇒
x = 1,5 cm
Questão 55
Um “cubinho” de gelo (c = 0,50 cal/(g.o C) e
Lf = 80 cal/g), de massa 20 g, se encontra
inicialmente a −20o C. A quantidade de calor
que esse gelo necessita para atingir a temperatura de 0o C e derreter totalmente é igual à
quantidade de calor que a massa de 100 cm3
de água (c = 1,0 cal/(g.o C) e ρ = 1,0 g/cm3 ) necessita para ter sua temperatura elevada de
20o C até:
b) 28o C
c) 36o C
a) 26o C
o
o
d) 38 C
e) 100 C
alternativa D
m
l
1,00 ⋅ 10 −1
4 ⋅ 0,50
⇒
= 4
⇒
=
⇒
k
g
k
10
⇒
k = 0,50 N/m
Como as quantidades de calor são iguais, temos:
Q g = Qa ⇒
⇒ m g ⋅ c g ⋅ ∆θ g + m g ⋅ Lf = ρ ⋅ V ⋅ ca ⋅ ∆θa ⇒
⇒ 20 ⋅ 0,50 ⋅ 20 + 20 ⋅ 80 = 1,0 ⋅ 100 ⋅ 1,0(θ − 20) ⇒
⇒ θ = 38 o C
Questão 54
Os termômetros são instrumentos utilizados
para efetuarmos medidas de temperaturas.
Os mais comuns se baseiam na variação de
volume sofrida por um líquido considerado
ideal, contido num tubo de vidro cuja dilatação é desprezada. Num termômetro em que
se utiliza mercúrio, vemos que a coluna desse
líquido “sobe” cerca de 2,7 cm para um aquecimento de 3,6 oC. Se a escala termométrica
fosse a Fahrenheit, para um aquecimento de
3,6o F, a coluna de mercúrio “subiria”:
a) 11,8 cm
d) 1,8 cm
b) 3,6 cm
e) 1,5 cm
c) 2,7 cm
Questão 56
Certo gás, considerado ideal, com massa 34 g,
está contido em um recipiente de 12,3 litros,
sob pressão de 4 atm a 27 o C. Considerando
apenas as massas atômicas dadas pela tabela
abaixo, assinale o gás contido no recipiente:
Dado: R = 0,082 atm ⋅ litro/(mol ⋅ K)
a) CH4
b) C2 H6
c) CO 3
d) NH 3
e) N2
Elemento Massa Atômica
H
1
C
12
N
14
O
16
física 5
alternativa D
Sendo o gás ideal, da equação geral de estado,
temos:
m
mRT
RT ⇒ M =
pV =
⇒
M
pV
34 ⋅ 0,082 ⋅ (273 + 27)
⇒M =
⇒ M = 17 g/mol
4 ⋅ 12,3
Assim, a massa molecular é 17 u, o que corresponde ao NH3 (MM NH3 = 14 + 3 ⋅ (1) ⇒
⇒ MM NH3 = 17 u).
Questão 57
Entre as placas de um condensador tem-se o
campo elétrico uniforme, de intensidade
1,0 ⋅ 105 V/m, ilustrado a seguir, e as ações
gravitacionais são desprezadas. Um corpúsculo eletrizado, de massa m = 1,0 ⋅ 10−3 g e
carga q = +2 µC , é abandonado do repouso
no ponto B. Após um intervalo de __________,
o corpúsculo passa pelo ponto ________, com
velocidade __________ .
⇒ |q | ⋅ E ⋅ d =
m ⋅ v C2
m ⋅ v B2
−
⇒
2
2
0
⇒ 2 ⋅ 10 −6 ⋅ 1 ⋅ 10 5 ⋅ 9 ⋅ 10 −3 =
1 ⋅ 10 −6 ⋅ v C2
⇒
2
⇒ v C = 60 m/s
Para o MUV, temos:
vB + vC
∆S
60
9 ⋅ 10 −3
=
⇒
=
⇒
∆t
∆t
2
2
0
⇒
∆t = 3,0 ⋅ 10 −4 s
Questão 58
Um chuveiro elétrico de valor nominal
(5 400 W - 220 V) deve aquecer de 20o C a
água que por ele passa. Para que isso ocorra,
a vazão da água deve ser aproximadamente:
Dados:
Densidade da água = 1 g/cm3
Calor específico da água = 1 cal/(g.o C)
1 cal = 4 J
a) 1 litro/minuto
c) 3 litros/minuto
e) 5 litros/minuto
A alternativa que contém as informações corretas para o preenchimento das lacunas na
ordem de leitura é:
a) 3,0 ⋅ 10−4 s; C; 60 m/s.
b) 3,0 ⋅ 10−4 s; A; 60 m/s.
c) 3,0 ⋅ 10−3 s; C; 60 m/s.
d) 3,0 ⋅ 10−3 s; A; 60 m/s.
e) 4 ,2 ⋅ 10−4 s; C; 85 m/s.
alternativa A
Como a carga é positiva, ela se desloca no sentido das linhas de campo, ou seja, de B para C.
Do Teorema da Energia Cinética (TEC), aplicado
no deslocamento de B a C, vem:
τ
C
Fel . B
= ∆E C ⇒
b) 2 litros/minuto
d) 4 litros/minuto
alternativa D
Considerando desprezíveis as perdas, sendo a
m
e c = 4 ⋅10 3 J/(kg ⋅ oC ),
∆t
temos:
vazão em massa Φm =
Q = mc∆θ
∆E = P ⋅ ∆t
Q = ∆E
⇒
⇒ mc∆θ = P ⋅ ∆t ⇒
⇒ Φm =
5 400
4 ⋅ 10
3
⋅ 20
m
P
=
⇒
∆t
c∆θ
⇒ Φm = 67,5 ⋅ 10 −3
kg
s
Considerando 1 kg de água correspondente a 1 litro, a vazão em litros por minuto é dada por:
Φ = 4 l/min
física 6
Questão 59
Observa-se que um resistor de resistência R,
quando submetido à ddp U, é percorrido pela
corrente elétrica de intensidade i. Associando-se em série, a esse resistor, outro de resistência 12 Ω e submetendo-se a associação à
mesma ddp U, a corrente elétrica que a atravessa tem intensidade i/4. O valor da resistência R é:
a) 2 Ω
b) 4 Ω
c) 6 Ω
d) 10 Ω
e) 12 Ω
alternativa B
Da definição de resistência elétrica e da associação em série dos resistores, temos:
U
U
i =
U
R
⇒ R =
⇒ R = 4Ω
i
U
4
R + 12
=
4
R + 12
campo magnético de vetor indução B, ficando
sujeita, por isso, à ação da força F. Com relação a esse fato, considere as afirmações abaixo:
I. v é sempre perpendicular a B
II. F é sempre perpendicular a B
III. F é sempre perpendicular a v
Assinale:
a) se todas as afirmações estão corretas.
b) se somente as afirmações I e II estão corretas.
c) se somente as afirmações II e III estão corretas.
d) se somente as afirmações I e III estão corretas.
e) se todas as afirmações estão incorretas.
alternativa C
Pela Regra da Mão Esquerda, a força magnética
é sempre perpendicular ao plano que contém os
Questão 60
Uma partícula eletrizada movimenta-se com
velocidade v, numa região onde existe um
vetores B e v (o ângulo entre B e v pode variar de
0 o a 180 o ). Assim estão corretas somente as afirmações II e III.