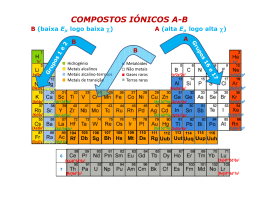
Ligação iónica
Compostos iónicos (resumo)
Os compostos iónicos são sólidos com temperaturas de fusão na ordem das centenas de
graus Celsius, são maus condutores eléctricos no estado sólido, apresentam durezas elevadas
e são pouco dúcteis, quebrando sem deformação por aplicação de um esforço de corte pouco
intenso. Estas propriedades derivam da natureza da ligação química nestes compostos,
designada ligação iónica.
Considera-se que a ligação entre dois átomos é iónica quando a respectiva diferença de
electronegatividades é muito elevada. Numa ligação iónica pura (%CI = 100%), os electrões de
valência são transferidos do átomo menos electronegativo para o mais electronegativo, daí
resultando catiões e aniões que se atraem electroestaticamente. Consequentemente, cada ião
rodeia-se de iões com carga de sinal contrário formando estruturas iónicas
compactas e
ordenadas (Fig. 1), com elevada energia de ligação (energia reticular), daí resultando as
elevadas temperaturas de fusão e as baixas maleabilidade e ductilidade dos cristais iónicos.
Figura 1 – Arranjo compacto de iões com carga de sinal contrário (estrutura do NaCl)
O diagrama de bandas de energia de um cristal iónico é caracterizado por uma banda de
valência totalmente preenchida e uma banda de condução vazia, separadas por uma elevada
diferença de energias (largura da banda proibida). Estas características são o resultado da
grande diferença de energia de ionização dos átomos constituintes e da transferência dos
electrões de valência do átomo menos electronegativo para o mais electronegativo. A banda de
valência deriva essencialmente das orbitais de valência do átomo mais electronegativo
(totalmente preenchidas no anião), e a banda de condução deriva das orbitais de valência do
átomo menos electronegativo (vazias no catião). Os cristais iónicos são assim isolantes
eléctricos.
Ligação iónica
A percentagem de carácter iónico %CI de uma ligação A-B aumenta com a diferença das
electronegatividades Δχ dos átomos A e B. A ligação iónica pura (%CI = 100%) corresponde
assim ao caso limite de uma diferença de electronegatividade infinita. Neste limite, ocorreria
transferência de um ou mais electrões da espécie menos electronegativa para a mais
electronegativa, e a ligação resultaria exclusivamente da interacção electrostática entre os iões
de sinais contrários, considerados esferas rígidas.
Admite-se que uma ligação é iónica quando a diferença de electronegatividade é superior a
2.0, quando os dois átomos envolvidos são não-metais, ou maior do que ~1.6, quando um dos
átomos envolvidos é um metal. Obviamente, trata-se duma aproximação, dado que, como %CI
é sempre menor que 100%, existe sempre contribuição covalente.
Considere-se as moléculas HCl e NaCl. Na primeira, a diferença de electronegatividades é
ΔχHCl = 0.96, e na segunda ΔχNaCl = 2.23. Na Fig.1 são comparadas as superfícies de
densidade electrónica das duas moléculas. No HCl, os electrões são partilhados embora o
cloro apresente um excesso de carga negativa (Fig. 1 a), enquanto no NaCl a superfície de
densidade electrónica calculada indica que não há praticamente partilha de electrões (Fig. 1b).
O ácido clorídrico HCl é uma molécula covalente polar, e o cloreto de sódio NaCl um composto
iónico.
Figura 1 - Superfície de densidade electrónica para a) HCl; b)NaCl.
È possível tratar a «molécula» NaCl à luz da TEV e estabelecer o respectivo diagrama de
orbitais moleculares. As energias das orbitais valência do Na têm valores muito diferentes das
do Cl e, de acordo com o critério da semelhança de energias para a formação de orbitais
moleculares, a interferência entre as orbitais atómicas dos dois átomos é pequena. Assim, as
orbitais ligantes são praticamente as orbitais de valência do Cl, e, pela mesma razão, as
orbitais anti-ligantes correspondem às orbitais de valência do Na (Fig.2). Na realidade, a
energia das orbitais OM2 a OM4 aumenta ligeiramente em relação à energia das orbitais 3p do
átomo de Cl isolado, uma vez que, com mais um electrão, aumentam as repulsões
interelectrónicas.
Figura 2 – Diagrama de orbitais moleculares da “molécula” de NaCl melhorar
A análise da Fig.2 indica que a contribuição covalente na molécula de NaCl (traduzida pelo
integral de ressonância) é praticamente inexistente, e a superfície de densidade electrónica da
+
-
Fig.1 sugere que esta espécie será melhor representada como Na Cl , sendo a contribuição
electrostática dominante.
Esta previsão é confirmada pela variação da energia potencial para a espécie diatómica NaCl
na fase gasosa em função da distância internuclear (Fig. 3). A electroafinidade do cloro é EA =
3.62 eV e a 1ª energia de ionização do sódio é EI = 5.14 eV o que significa que «custa» 1.52
+
eV transferir um electrão do sódio para o cloro. A atracção electrostática entre os iões Na e Cl
-
iguala estes 1.52 eV para uma distância de 941 pm. Para a distância internuclear de equilíbrio
+
-
(236 pm), o sistema Na Cl é 4.26 eV mais estável do que os átomos de Cl e Na isolados.
+
-
Figura 3 - Diagrama de energia potencial para a espécie iónica Na Cl na fase gasosa.
O NaCl e os compostos iónicos em geral não existem na forma diatómica, mas na forma
cristalina (NaCl)N, em que N é um número muito grande, tal como nos metais e cristais
covalentes.
A descrição mais comum, embora pouco rigorosa, da ligação em cristais iónicos consiste assim
em considerar que há transferência de um ou mais electrões entre os átomos envolvidos, com
formação de iões de cargas de sinal contrário que se atraem mutuamente. O modelo trata os
iões como esferas rígidas carregadas que se dispõem em estruturas cristalinas
de modo a
maximizar as atracções electrostáticas entre iões com carga de sinal contrário e minimizar as
repulsões entre iões com carga do mesmo sinal. Implicitamente, uma vez que não se considera
qualquer interacção orbital entre os iões, as interacções entre iões são adireccionais e a
coordenação de um determinado ião é apenas dependente de factores geométricos.
No entanto, algumas estruturas cristalinas de compostos iónicos não são justificadas por
factores meramente geométricos. Também uma análise das energia reticulares calculadas
com base no modelo da ligação iónica puramente electrostática mostra que, embora para
compostos como o NaCl ou o KI haja uma boa concordância entre os valores experimentais e
os valores calculados, para outros compostos, por exemplo sais de prata ou cádmio, os valores
experimentais calculados com base no ciclo de Born-Haber são francamente superiores aos
calculados com base no modelo. A discrepância pode ser atribuída à contribuição covalente da
ligação, o que explica igualmente as estruturas «anómalas» de alguns compostos. De facto,
não há ligações completamente iónicas e, se o modelo das esferas rígidas carregadas é uma
boa aproximação para compostos como o NaCl, muitos compostos normalmente descritos
como iónicos requerem modelos mais elaborados da ligação iónica que contemplem a
combinação linear das orbitais atómicas dos átomos envolvidos e a formação de bandas de
níveis energia.
Mesmo para o LiF, um composto com elevada percentagem de carácter iónico, no mapa de
densidade electrónica obtida por difracção de Raios-X (H. Witte and W. Woelfel, Reviews of
Modern Physics, 30, 53, (1958), verifica-se que a densidade electrónica em torno do lítio não é
circular, o que indica que há partilha de electrões entre o Li e o F, ou seja, é uma evidência
experimental de que há uma contribuição covalente na ligação Li-F.
Energia Reticular
No modelo da ligação iónica, esta é assegurada por interacção electrostática entre iões de
sinais contrários, considerados esferas rígidas. A energia correspondente à interacção de dois
iões é dada pela lei de Coulomb:
ECoulomb= - 1/4πε0 × ZCZA/r
(1)
em que ZC e –ZA são, respectivamente, as cargas do catião e do anião, r é a distância entre os
iões, assumida como a soma do raio iónico do catião com o raio iónico do anião, e ε0 é a
constante dieléctrica do vácuo.
Numa rede cristalina, cada ião está sujeito a interacções electrostáticas com todos os outros
que o rodeiam. A energia reticular (U) de um dado composto iónico é assim a soma de todas
as interacções electrostáticas na rede tridimensional do cristal iónico e corresponde à energia
posta em jogo na reacção de formação de uma mole de um cristal iónico a partir dos iões
constituintes no estado gasoso perfeito, a 0 K, representada na Eq. 2.
m+
n-
n' A (g) + m' B (g) -----> An'Bm' (s)
(2)
Na Eq. 2, m' e n' são os coeficientes estequiométricos que asseguram a neutralidade eléctrica
do sal formado (quando m ou n=1, como por exemplo no NaCl e MgCl2, m=m' e n=n').
A energia reticular, U, tem duas componentes: uma componente coulômbica que dá conta das
interacções electrostáticas (atractiva e repulsiva) de todos os iões da rede, U’, e a energia de
repulsão electrão-electrão dos electrões de iões adjacentes, U’’.
A primeira componente, U’, é o somatório de todas as interacções, atractivas e repulsivas,
exercidas sobre um determinado ião pelos iões vizinhos. Por simplicidade, considere-se um
cristal linear de NaCl, representado parcialmente na Fig.1, em que as distâncias entre iões
adjacentes são r (neste cristal, r = 253 pm).
Figura 1 - Cristal unidimensional de NaCl.
+
As interacções exercidas sobre o catião Na central, representado a vermelho, são atractivas
com os 2 aniões que se encontram à distância r, 3r, 5r, 7r, etc., e repulsivas com os 2 catiões
que se encontram à distância 2r, 4r, 6r, 8r, etc. Portanto, U’ terá a expressão:
2
2
2
2
2
2
U’Na+ = 1/4πε0 [-2e /r + 2e /2r - 2e /3r + 2e /3r - 2e /5r + 2e /6r + …] =
2
= -1/4πε0 × 2e /r (1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + ...)
(3)
O termo entre parênteses é uma série infinita convergente cujo limite é ln2 e não depende dos
iãos em causa; decorre da estrutura em causa. Este factor geométrico é designado por
constante de Madelung, A, e é característico de uma determinada rede cristalina.
Uma vez que existem 2NA iões numa mole de cloreto de sódio, para calcular a energia reticular
do cristal linear seria necessário multiplicar a equação 2 por 2NA mas para não contabilizarmos
-
duas vezes a mesma interacção (a interacção entre o ião central com o ião Cl identificado com
2 é contada quando consideramos as interacção do ião central e as interacções do ião 2 ), a
energia reticular num cristal linear é dada pela Eq. 4.
2
U’ = - NA2e A / 4πε0 r
(4)
A energia de interacção repulsiva entre as nuvens electrónicas de iões adjacentes U’’ é
contabilizada no termo (1-1/n) na Eq. 5, designada equação de Born-Meyer:
2
U = -NA2e A / 4πε0 r× (1-1/n)
(5)
O valor de n é obtido da compressibilidade dos cristais e é característico do tipo de
configuração electrónica do ião. Os iões isoelectrónicos com a configuração electrónica do He,
Ne, Ar, Kr e Xe têm valores de n iguais a 5, 7, 9, 10 e 12, respectivamente. Se um cristal
contiver iões com diferentes configurações electrónicas, utiliza-se o valor médio de n. Por
exemplo, para o NaCl, utiliza-se o valor 8, e para o LiF o valor
6.
Estruturas iónicas – estequiometria 1:1
A maximização da energia reticular implica que um determinado composto iónico adopte a
estrutura cristalina em que, simultaneamente, é minimizada a distância r entre iões adjacentes
e em que cada ião se rodeia do maior número de iões de carga oposta possível. Assim, um
composto iónico «ideal» apresentará uma estrutura tão compacta quanto possível, em que o
número de vizinhos, o número de coordenação da estrutura em causa, será o maior permitido
pelas dimensões relativas dos iões. As estruturas dos cristais iónicos podem então ser
consideradas estruturas compactas de iões, em que os iões de carga contrária preenchem
interstícios, octaédricos e/ou tetraédricos, ou estruturas compactas de iões, dos quais parte é
substituída por iões de carga contrária. Daqui resultam os números de coordenação mais
habituais das estruturas iónicas, respectivamente, 8 (coordenação cúbica), 6 (coordenação
octaédrica) e 4 (coordenação tetraédrica).
Estrutura do tipo CsCl
As estruturas de compostos AB com número de coordenação 8 correspondem a compostos em
que os iões apresentam dimensões semelhantes. Esta estrutura é designada estrutura do tipo
cloreto de césio, representada na Fig. 1, e pode considerada uma estrutura CCC, na qual
foram substituídos 50 % dos iões cloreto por iões césio.
Figura 1 - Célula unitária primitiva da estrutura do cloreto de césio. Dentro da célula unitária há um
catião e um anião.
O ião césio ocupa na Fig. 1 o centro do cubo e encontra-se rodeado por 8 iões cloreto (e viceversa), ou seja, os números de coordenação são (8:8). O valor da constante de Madelung
para esta estrutura é 1.763.
+
Imagine-se que é substituído o ião Cs por um ião de menor dimensão. À medida que a
dimensão do catião diminui, os aniões circundantes aproximam-se até contactarem. Nesta
situação (rC/rA = 0.732, a repulsão interaniónica torna a estrutura instável, sendo mais favorável
um número de coordenação menor do que 8, de modo a evitar o contacto dos aniões de
coordenação. Para rC/rA < 0.732, a coordenação passa de 8 para 6. O valor 0.732 designa-se
razão crítica de transição de uma coordenação cúbica para uma coordenação octaédrica. As
estruturas cristalinas resultantes correspondem a estruturas compactas de aniões em que os
catiões preenchem os interstícios octaédricos.
Estrutura do tipo CsCl
Uma dessas estruturas é designada estrutura do tipo cloreto de sódio e corresponde a uma
estrutura CFC de aniões em que os catiões preenchem todos os interstícios octaédricos e é
representada na Fig. 2.
Figura 2 – Célula base do cloreto de sódio. Cada ião está rodeado de 6 contra-iões. No cubo existem 4
aniões e 4 catiões.
A estrutura do tipo NaCl, com uma coordenação 6:6, é mantida para compostos em que o raio
do catião é igual ou maior do que o raio do interstício octaédrico, isto é, para sais em que a
razão rC/rA ≥ 0.414. Para esta razão crítica os aniões (ou catiões se forem maiores do que os
aniões) entram em contacto tornando o arranjo instável. Quando rC/rA < 0.414, a coordenação
4:4 torna-se mais estável e os compostos apresentam estruturas cristalinas que podem ser
consideradas como derivadas de estruturas compactas por preenchimento de interstícios
tetraédricos.
Estrutura do tipo ZnCl (blenda)
Os raios iónicos do Zn
2+
2-
e do S são, respectivamente, rC= 74 pm rA= 184 pm, o que dá rC/rA =
0.402, menor do que a razão crítica 0.414. Consequentemente, o Zn
2+
terá número de
coordenação 4, e, uma vez que numa estrutura CFC há na célula unitária o dobro dos
interstícios tetraédricos em relação ao número de átomos, o catião ocupa metade dos
interstícios tetraédricos. A estrutura do ZnCl (blenda), designada tipo blenda, é mostrada na
Fig. 3.
Figura 3 - Célula base da estrutura da blenda, ZnS. Na célula base há 4 catiões e 4 aniões.
Na coordenação tetraédrica, a situção de contacto e repulsão dos contraiões ocorre para rC/rA =
0.225, pelo que este tipo de estruturas se encontra em compostos iónicos cuja razão rC/rA se
encontra compreendida no intervalo 0.414 > rC/rA > 0.225.
As estruturas do tipo CsCl, NaCl e ZnS (blenda) são as estruturas mais comuns dos sais
iónicos binários com estequiometria 1:1, e aparentemente ditadas exclusivamente por
condicionamentos geométricos (razão rC/rA). No entanto, este não é o único factor que as
determina: não há ligações 100% iónicas. Assim, e por exemplo, para uma razão de raios que
imponha que o ião positivo ocupe um interstício tetraédrico, num dado composto o interstício
tetraédrico poderá pertencer a uma estrutura CFC de iões negativos, enquanto noutro
composto diferente pertencer a uma estrutura HC, cujos interstícios têm a mesma dimensão.
De facto, o sulfureto de zinco apresenta uma forma alotrópica designada wurtzite que
corresponde a uma estrutura HC de aniões em que os catiões ocupam metade dos interstícios
tetraédricos (Fig. 4).
Figura 4 - Célula unitária primitiva da estrutura da wurtzite, ZnS. Clicando no botão «Ver HC», são
mostradas várias células e é destacada a vermelho a célula hexagonal compacta, HC.
Em relação à coordenação octaédrica, existe para além da estrutura tipo NaCl, a estrutura tipo
arsenieto de níquel, NiAs, (Fig. 5) que consiste numa estrutura HC de aniões em que os
catiões preenchem os intersticíos octaédricos.
Figura 5 - Célula unitária primitiva do arsenieto de níquel, NiAs.
Para além disso, muitos compostos apresentam estruturas inesperadas à luz deste modelo de
esferas rígidas. Em geral, a coordenação prevista pela razão de raios iónicos é verificada nos
compostos em que a percentagem de carácter iónico é muito elevada, tipicamente os
halogenetos e os óxidos dos metais dos grupos 1 e 2. Com o aumento da percentagem de
carácter covalente, o modelo puramente geométrico deixa de funcionar. Por exemplo, na Fig. 6
é representada a estrutura
do cinabre, sulfureto de mercúrio, HgS - (do latim cinnabar,
designa um pigmento natural extensivamente utilizado na Antiguidade, da cosmética à arte.
Depois de Teofrasto o ter descrito, por volta do ano 300 a.C, passou a ser uma fonte frequente
do mercúrio usado em metalurgia e alquimia). No cinabre, o Hg
2+
liga-se a dois S
geometria linear.
Figura 6 - Célula unitária primitiva do cinabre, HgS.
2-
numa
Estruturas iónicas: outras estequiometrias
As estruturas de compostos iónicos AB2 consideradas como estruturas CFC ou HC de iões
com preenchimento de interstícios pelos respectivos contra-iões dependem igualmente da
razão rC/rA. Uma estrutura muito vulgar nos compostos do tipo AB2 é a estrutura da fluorite
(fluoreto de cálcio, CaF2), na qual o número de iões fluoreto é duplo do de iões cálcio. Os iões
fluoreto ocupam 100% dos interstícios tetraédricos de uma estrutura CFC de iões cálcio (Fig.
1), ficando rodeado por 4 iões cálcio. Um ião de cálcio, por sua vez, tem 8 fluoretos como
primeiros vizinhos (coordenação 8:4). A coordenação cúbica dos iões cálcio é a esperada com
base na razão dos raios iónicos do Ca
2+
-
e do F (rC/rA = 0.73).
Figura 1 - Célula unitária da fluorite, CaF2.
Outra estrutura muito comum é designada estrutura anti-fluorite (Fig. 2) e é apresentada por
compostos como o óxido de sódio, Na2O, que, por restrições estequiométricas, consiste numa
estrutura CFC de catiões em que os aniões ocupam todos os interstícios tetraédricos
(coordenação 4:8).
Figura 2 - Célula unitária da anti-fluorite, CaF2.
Quando as dimensões do catião diminuem, isto é a razão rC/rA diminui abaixo da razão crítica a
coordenação do catião passa de cúbica para octaédrica e surgem estruturas CFC (estrutura do
cloreto de cádmio, Fig. 3a ) ou HC (estrutura do iodeto de cádmio e do rutilo, Fig 3b) de com
preenchimento de interstícios octaédricos.
Figura 3 - Células unitárias primitivas das estruturas, a) cloreto de cádmio, CdCl2; b) iodeto de cádmio,
CdI2 e rutilo, TiO2.
As estruturas de compostos de alguns compostos AB3 e A2B3 podem igualmente ser
consideradas derivadas de estruturas compactas por preenchimento de interstícios. No caso
das estruturas AB3, indicam-se as estruturas do tipo CrCl3, uma estrutura CFC de aniões em
que os catiões ocupam 1/3 dos interstícios octaédricos, e a estrutura do tipo BiI3, análoga à
anterior mas em que os aniões definem uma estrutura HC. Em relação a sais iónicos A2B3, uma
estrutura muito comum é uma estrutura do tipo da alumina, Al2O3, representada na Fig. 4 e na
qual os iões Al
3+
2-
ocupam 2/3 dos interstícios octaédricos de uma rede CFC de iões O .
Figura 4 - Célula unitária primitiva da alumina, Al2O3. Clicando nos botões apropriados pode ver outras
células para compostos iónicos A2B3.
Existem ainda compostos iónicos com mais de dois iões na estrutura, como sejam sais mistos
e sais de aniões complexos. Na Figura 10 são indicadas como exemplo as estruturas da
calcite, CaCO3, e de uma perovskite de fórmula Ba2Cu3O6Y. As perovskites, assim nomeadas
em homenagem a L. A. Perovski, constituem uma classe de compostos com propriedades
muito interessantes que encontram aplicação em eléctrodos catalíticos para certos tipos de
células de combustível e que são candidatos a aplicações em spintrónica.
Figura 10 - Estrutura da: a) calcite; b) perovskite Ba2Cu3O6Y.
Energia Reticular e Ciclo de Born Haber As energias reticulares podem ser determinadas através de um ciclo de Born-Haber, um
ciclo termodinâmico que assenta na lei de Hess. A entalpia (calor a pressão constante) é
uma função de estado pelo que a variação de entalpia associada a uma reacção não
depende do seu percurso, depende apenas dos estados final e inicial do sistema. Assim,
podemos analisar a energética da formação de um composto iónico a partir dos
elementos constituintes (a sua entalpia de formação), considerando a energética dos
passos em que se pode dividir a reacção de formação.
Exemplificando com o fluoreto de lítio, a entalpia de formação do LiF corresponde à
variação de entalpia associada ao processo de formação do LiF a partir dos elementos
constituintes:
Li (s) + ½ F2 (g) →
LiF (s)
ΔHfº (LiF) = -594,1 kJ
A energia reticular do LiF que se pretende calcular corresponde à variação de entalpia
associada ao processo:
Li+ (g) + F- (g)
→
ΔHº = U (LiF)
LiF (s)
Este valor pode ser calculado se dividirmos a reacção global em passos.
1. Sublimação do lítio:
Li (s) →
Li (g)
ΔHso (Li) = 155,2 kJ
Li+ (g) + 1 e-
ΔHº = I1 (Li) = 520 kJ
2. Ionização do lítio:
Li (g) →
3. Dissociação do flúor:
½ F2 (g) →
ΔHº = ½ ΔHºdiss (F2) = 150.6/2 = 75.3 kJ
F (g)
4. Ionização do flúor:
F (g) + 1 e- →
F- (g)
ΔHº = EA (F) = - 328 kJ
sendo o passo seguinte a formação da rede cristalina:
Li+ (g) + F- (g)
→
LiF (s)
ΔHº = U (LiF)
A entalpia da reacção de formação do LiF deverá ser igual à soma das entalpias dos
vários passos através dos quais ocorre esse processo, isto é:
Li (s) →
Li (g)
ΔH1º = ΔHso(Li)= 155,2 kJ
Li (g) →
Li+ (g) + 1 e-
ΔH2º = I1 (Li) = 520 kJ
½ F2 (g) → F (g)
ΔH3º = ½ ΔHºdiss (F2) = 150,6/2 = 75,3 kJ
F (g) + 1 e- →
ΔH4º = EA (F) = - 328 kJ
F- (g)
Li+(g) + F- (g) →
LiF (s)
Li (s) + ½ F2 (g) →
LiF (s)
ΔH5º = U (LiF)
ΔHfº (LiF) = -594,1 kJ
Somando as entalpias das reacções parcelares e igualanda-as à entalpia de formação do
LiF, calcula-se a energia reticular neste cristal.
ΔHfº (LiF) = ΔHsº + I1 (Li) + ½ ΔHºdiss (F2) + A (F) + U (LiF) ó
ó -594,1 = 155,2 + 520 + 75,3 - 328 + U (LiF) ó U (LiF) = -1017 kJ/mol
A formação de LiF sólido a partir dos seus elementos, representada esquematicamente
na figura 1, é muito exotérmica devido essencialmente à energia reticular. De facto,
neste caso concreto, a formação de iões isolados, a partir de átomos da Li e F é um
processo endotérmico e termodinamicamente desfavorável.
Figura 1 – Ciclo de Born Haber para o LiF.
O valor da energia reticular depende da distância interiónica (link tópico ligação), da
carga dos iões e da estrutura cristalina. A constante de Madelung varia pouco para
estruturas com a mesma estequiometria como indicado na Tabela 1:
Tabela 1 - Valores da Constante de Madelung para algumas Estruturas Cristalinas
Estrutura
Nº Coord.
Iões
A
Cloreto de sódio
6:6
A+,B- ou A2+,B2-
1,748
Cloreto de césio
8:8
A+,B-
1,763
Blenda
4:4
A+,B-
1,638
Wurtzite
4:4
A+,B-
1,641
Fluorite
8:4
A2+,2B-
2.519
Rútilo
6:3
A2+,2B-
2.408
Al2O3
6:4
2A3+,3B2-
4.172
Utilizando a equação de Born-Meyer é assim possível calcular a energia reticular de
compostos iónicos assumindo uma ligação 100% iónica. Alguns dos valores calculados
são comparados na Tabela 2 com os valores «experimentais» obtidos a partir de ciclos
de Born-Haber.
Tabela 2 – Comparacão da energia reticular experimental e calculada
-U exp/kJ.mol-1
-Ucalc/kJ.mol-1
NaBr
747
732
NaCl
786
769
KCl
715
701
AgCl
915
864
AgBr
904
830
LiF
1036
1030
MgO
3791
3795
Fe2O3
14309
14774
MgCl2
2526
2326
MgI2
2327
1944
CaI2
2074
1905
CdCl2
2552
2226
Composto
O valor calculado assumindo que a ligação nestes compostos é puramente electrostática
dá resultados muito próximos dos obtidos através de ciclos de Born-Haber para a
maioria dos compostos na tabela 2. No entanto, em alguns compostos há uma diferença
significativa entre os valores calculados e os valores obtidos do ciclo termodinâmico.
Por outro lado, quando há contribuição covalente a separação de cargas não é completa,
isto é, não temos exactamente Na+ e Cl-, por exemplo, mas Naδ+ e Clδ-. Estamos assim a
calcular a contribuição electrostática por excesso e na maior parte dos casos esse
excesso compensa a contribuição covalente. Essa compensação não funciona em
compostos com uma significativa contribuição covalente, por exemplo no CdCl2 que
apresenta uma diferença de electronegatividades de Δχ= 1.47 e está nos limites da
ligação iónica, e em que há uma diferença de cerca de 15% por defeito no valor
calculado usando o modelo da ligação 100% iónico em relação ao valor «experimental».
No entanto, no CdI2, em que a diferença de electronegatividade de apenas Δχ= 0.96 o
colocaria nos cristais covalentes, a diferença entre o valor calculado assumindo carácter
100% iónico e o «experimental» é menor que no cloreto. Este facto poderia indicar uma
menor contribuição covalente nesta espécie mas o que na realidade se passa é mais
complexo.
Os iões num cristal de compostos 100% iónicos apresentam nuvens electrónicas
esféricas. Quando o catião é pequeno e/ou com carga elevada, polariza a nuvem
electrónica do anião distorcendo-a. A polarização da nuvem electrónica do anião leva à
existência de densidade electrónica na zona internuclear, ou seja, aumenta o carácter
covalente da ligação. Quanto maior for o anião, mais facilmente este é polarizado e
quanto menor o catião e mais carregado maior o efeito que exerce sobre o contra-ião.
Por exemplo, o AlCl3 com Δχ= 1.55 é um composto molecular de formula Al2Cl6, isto
é, aparece não na forma de cristal iónico mas sim de composto covalente. De igual
forma o TiCl4, com Δχ= 1.62, é um líquido molecular com temperatura de ebulição
136.5°. Em ambos os casos, o catião apresenta um raio muito pequeno e carga muito
elevada (rAl3+= 50 pm; rTi 4+= 56 pm).
O modelo iónico é assim apenas isso, um modelo muito simples que funciona bem para
muitos compostos iónicos, mas que não corresponde na maioria dos casos ao que de
facto acontece aos electrões de valência destes compostos. Para uma discussão mais
sustentada destes compostos, nomeadamente das suas propriedades eléctricas, torna-se
necessário considerar a sua “estrutura electrónica”, abordada de forma qualitativa com
base na extensão a compostos iónicos da Teoria das Orbitais Moleculares
TOM Aplicada a Compostos iónicos
Não obstante o sucesso do modelo das esferas rígidas, é evidente que a ligação dita
iónica tem algum carácter covalente, e portanto direccional, claramente exibido por
substâncias iónicas nas quais o carácter covalente é apreciável. Por exemplo, a estrutura
do cinabre, HgS, só pode ser entendida se se admitir que as ligações são determinadas
essencialmente pela sobreposição orbital. De facto, a razão rC/rA = 0.598 indica que o
mercúrio deveria apresentar uma coordenação octaédrica e não apresentar apenas dois
S2- em primeira vizinhança numa geometria linear (Fig.1).
A direccionalidade da
ligação é assim mais uma manifestação da natureza parcialmente covalente da ligação
dita iónica.
Figura 1 – Distâncias Hg-S no cinabre, evidenciado a coordenação 2 linear do ião Hg
2+
.
A determinação experimental das energias dos electrões num composto iónico pode ser
efectuada por recurso aos mesmos métodos espectroscópicos utilizados para metais. Os
resultados obtidos indicam que, tal como nos cristais covalentes, existem nestes compostos
pelo menos duas bandas de energia, uma preenchida designada banda ligante (banda de
valência), e uma banda vazia – a banda anti-ligante ou banda de condução, separadas por
uma energia elevada (largura da banda proibida link para cristais covalentes).
Esta estrutura de bandas, determinada experimentalmente, pode ser explicada de forma
qualitativa considerando as combinações lineares das orbitais atómicas (TOM/CLOA) dos
átomos envolvidos, tendo em conta que num cristal iónico existe um número muito elevado de
iões.
Considere-se por exemplo o NaCl e o diagrama de energias da respectiva “molécula”.
+
-
Considerando que no cristal existirão N catiões Na e N aniões Cl , é possível conceber as
orbitais da “molécula” dando origem a bandas de níveis de energia estreitas quase
isoenergéticas com as orbitais “moleculares” de origem. A orbital OM1 dará origem a uma
banda preenchida (com N níveis e 2N electrões), o conjunto das orbitais OM2, OM3 e OM4
dará origem a outra banda também preenchida (com 3N níveis e 6 N electrões), e duas bandas
vazias com origem no conjunto OM5, OM6 e OM7 (3N níveis) e na OM8 (N níveis). O diagrama
de orbitais moleculares qualitativo resultante será o indicado na Fig.2.
Figura 2 - Diagrama de orbitais moleculares para um cristal iónico AB em que A e B
apresentam apenas uma orbital de valênciaA estrutura electrónica resultante é típica de um isolante ou de um semicondutor, dependendo
da largura da banda proibida. A largura da banda proibida está relacionada com a diferença de
energias EB-EA indicadas na Fig.2. As energias EA e EB, são, numa primeira aproximação, o
simétrico das energias de ionização de A e de B. No entanto, devido ao rearranjo electrónico
que conduz a um aumento das repulsões interelectrónicas quer por emparelhamento de
electrões quer por maior confinamento espacial, todo o diagrama sofre uma translação para
maiores energias ficando EX (onde X pode ser A ou B) a meio caminho entre a energia de
ionização e a electroafinidade (ver diagrama de energias para a espécie diatómica NaCl).
Assim, uma boa medida da diferença EB-EA deverá ser a diferença de electronegatividades
Δχ=χB−χA. Na Fig. 3, representa-se a largura da banda proibida (Eg), para vários compostos
iónicos, em função de Δχ. Obtém-se uma boa correlação entre as duas grandezas, correlação
que pode ser melhorada se se usar a diferença de electronegatividades «corrigida», (χA1/2
1/2
1.75) +(χB-1.75) , que dá conta do valor médio das electronegatividades. De facto, quanto
maior for a média das electronegatividades, mais “agarrados” estão os electrões aos
respectivos núcleos e menor é a deslocalização, logo menor é o alargamento das bandas e,
portanto, para uma mesma diferença de electronegatividades, maior é a largura da banda
proibida.
Propriedades físicas de compostos iónicos Temperatura de fusão e ebulição Os compostos iónicos apresentam propriedades físicas que envolvem a separação dos iões da
rede cristalina, nomeadamente a temperatura de fusão e ebulição, a dureza ou a solubilidade,
e que por isso dependem da energia reticular.
As temperaturas de fusão e de ebulição dos compostos iónicos são particularmente elevadas,
quando comparadas com as dos compostos moleculares, e de ordem de grandeza semelhante
às dos metais, em concordância com os valores geralmente elevados da energia reticular.
As temperaturas de fusão e de ebulição podem ser correlacionas com a energia reticular. Na
Fig.1 são indicadas as temperaturas de fusão dos halogenetos dos metais alcalinos e da prata
em função da energia reticular calculada com base em ciclos de Born-Haber.
1050 950 LiF 850 750 LiCl 650 AgI 550 LiI 450 350 550 650 750 AgCl AgF AgBr 850 950 1050 1150 Figura 1 –Correlação entre energia reticular e temperatura de fusão dos halogenetos de metais
alcalinos e da prata.
A Fig. 1 permite concluir que as temperaturas de fusão destes compostos iónicos é
relativamente bem comportada, observando-se um aumento regular da Tf com a energia
reticular. Os compostos que saem deste comportamento, são os sais de lítio e prata, que
apresentam temperaturas de fusão mais baixas que o esperado, os primeiros devido à
pequena dimensão do catião que apresenta um efeito polarizador muito elevado
e os
segundos provavelmente devido ao elevado carácter covalente que já era notado na
comparação dos valores «experimentais» e calculados da energia reticular.
O mesmo tipo de comportamento é mantido se se alargar a correlação de forma a incluir os
halogenetos de metais alcalino-terrosos e de cádmio e os óxidos de dois metais alcalinos e dos
metais alcalino terrosos (Fig. 2).
3500 CaO 3000 MgO BeO SrO 2500 2000 BaO 1500 1000 BeI2 500 CdCl2 CdI2 0 0 1000 2000 BeF2 BeCl2 3000 4000 5000 Figura 2 –Correlação entre energia reticular e temperatura de fusão para os halogenetos de
metais alcalinos, alcalino terrosos, cádmio e prata e para os óxidos dos metais alcalino
terrosos, Li e Na (para estes últimos, foi utilizado o valor de energia reticular calculado com a
equação de Born-Meyer).
Mais uma vez observamos que os sais de metais de pequenas dimensões, independentemente
da carga do contra-ião, e os sais em que existe uma elevada contribuição covalente,
apresentam temperaturas de fusão mais baixas que o previsto com base na energia reticular.
Por outro lado, verifica-se que os compostos de iões bivalentes, quer compostos AB quer AB2,
apresentam temperaturas de fusão mais baixas que o esperado com base na correlação
obtida para os compostos AB de iões monovalentes «bem-comportados». Tudo isto confirma
que o modelo da ligação 100% iónica, embora nos permita uma certa capacidade de previsão
de propriedades físicas e preveja o andamento geral destas, falha nos pormenores e deve ser
aplicado com precaução.
Propriedades físicas de compostos iónicos Dureza, fragilidade e indeformabilidade Alguns dos materiais mais duros que se conhece são compostos iónicos, nomeadamente a
alumina, Al2O3, quando na forma de monocristal (safira), apresenta uma dureza muito elevada,
imediatamente abaixo do diamante, 9 na escala de Mohs. A dureza é medida pela capacidade
de um dado cristal se deixar riscar por outro (mais duro), ou seja, mede a maior ou menor
facilidade com que é possível separar a rede cristalina. A dureza relativa é então outra
propriedade que segue em paralelo com a energia reticular e a elevada energia reticular na
alumina explica a dureza das safiras (quando a alumina inclui impurezas com o ferro, cobalto
ou titânio as safiras são azuis; a inclusão de crómio
muda a cor para vermelho -rubis).
Também nos óxidos dos metais alcalino-terrosos a dureza segue o andamento esperado como
ilustrado na Fig. 1.
7 6.5 MgO 6 5.5 5 4.5 CaO 4 3.5 3 3000 SrO BaO 3100 3200 3300 3400 3500 3600 3700 3800 3900 Figura 1 – Dureza relativa na escala de Mohs para óxidos dos metais alcalino-terrosos em
função da energia reticular calculada com base no ciclo de Born-Haber.
Os materiais iónicos são, no entanto, muito frágeis, independentemente da sua dureza. Um
material é frágil quando quebra sem praticamente se deformar por aplicação de um esforço de
corte - mais ou menos intenso consoante o a material. O que acontece é bem ilustrado na Fig.2
que mostra que uma pequena deslocação de camadas do cristal pode pôr em contacto iões da
mesma carga e a repulsão electrostática resultante é suficiente para partir o cristal.
Figura 2 - Fragilidade dos compostos iónicos: representação esquemática da acção de uma
tensão de corte sobre dois planos conduzindo à separação dos dois planos.
O esquema da Fig. 1 ajuda também a perceber a razão pela qual os cristais iónicos são
indeformáveis: uma pequena deformaçãotem o mesmo efeito de uma tensão de corte e conduz
à quebra do material.
Propriedades físicas de compostos iónicos
Solubilidade
Os compostos iónicos são normalmente solúveis (embora nem todos na mesma extensão) em
solventes polares, em particular em água. Quando se dissolve um sal iónico em água, por
exemplo NaCl, o sal dissocia-se nos iões constituintes, neste caso Na
+
-
e Cl , que são
solvatados por interacções ião-dipolo. A água dispõe-se em volta dos iões com o oxigénio
voltado para os catiões e os hidrogénios para os aniões como ilustrado na Fig. 1.
Figura 1 (Refazer neste género, esta foi roubada da net)
A maior ou menor solubilidade de um sal decorre então do balanço entre a energia gasta no
processo (a energia reticular) e a energia libertada (a energia de solvatação). Quanto mais
negativo for esse balanço, isto é, quanto menor for, em módulo, a energia reticular e maior for a
energia de solvatação, em módulo, maior é a solubilidade.
Os sais com uma energia reticular muito elevada, por exemplo, a alumina, são insolúveis em
água porque a energia de solvatação não compensa a energia reticular. Mas na maioria dos
casos não é fácil avaliar relativamente as magnitudes das duas interacções postas em jogo e
não há uma correlação da solubilidade de um sal com a energia reticular.
O módulo da energia reticular é proporcional ao inverso de rc+rA (link ligação iónica). A
solvatação, por sua vez, ocorre essencialmente através de interacções dipolo-ião cuja
intensidade vai depender do inverso do tamanho do ião: quanto mais pequeno este mais forte é
a interacção (porque a carga, negativa ou positiva, está mais «concentrada»). No entanto, há
também que ter em conta o número de moléculas de água que se podem dispor em trono de
um determinado ião e a energia de solvatação é maior para iões de maiores dimensões, ou
seja, é proporcional a 1/rc+1/ra. Por outro lado, quer as interacções ião dipolo quer a energia
reticular aumentam com a carga do ião. Isto significa que quer a energia reticular quer a
energia de solvatação dependem das dimensões e das cargas dos iões mas a sua variação
tem efeitos diferentes em ambas no caso dos tamanhos dos iões e actua em sentidos opostos
na solubilidade no caso da carga.
A previsão da solubilidade de um composto iónico é assim difícil de conseguir embora sejam
distintos alguns padrões de comportamento. Uma desses padrões encontra-se na solubilidade
dos halogenetos de metais alcalinos. A solubilidade destes sais é tanto maior quanto mais
diferentes forem as dimensões dos iões envolvidos. No caso dos fluoretos – o mais pequeno
dos aniões halogeneto - os sais mais solúveis são os que contêm os maiores catiões e o CsF é
cerca de 240 vezes mais solúvel que o LiF. Quando se passa para os iodetos – o maior anião –
, os sais mais solúveis são os que contêm os catiões mais pequenos: a solubilidade do LiI é
12.3 mol /L enquanto a do CsI é apenas de 1.7 mol /L.
Outras generalizações com base em evidências experimentais traduzem-se em regras de
solubilidade. Por exemplo, os nitratos e sulfatos, em que o anião é muito grande, são muito
solúveis, com excepção dos compostos BaSO4, PbSO4, and SrSO4. De igual forma, os cloretos
são normalmente solúveis, sendo AgCl, Hg2Cl2 e PbCl2 os únicos cloretos macroscopicamente
insolúveis em água. Carbonatos, hidróxidos e sulfuretos são insolúveis, com excepção dos
sais de metais alcalinos (e metais alcalino terrosos no caso dos sulfuretos), do carbonato e
sulfureto de amónio, Ba(OH)2, Sr(OH)2. O Ca(OH)2 apresenta uma solubilidade muito baixa.