SUPERFÍCIE E CURVA 1
SUPERFÍCIE E
CURVA
As superfícies são estudadas numa área chamada de Geometria Diferencial, desta
forma não se dispõe até o nível da Geometria Analítica de base matemática para
estabelecer o conceito de superfície; entretanto, é neste momento que são estudados vários
exemplos de superfícies, que serão aplicados para desenvolver o Cálculo e por sua vez é
onde se apóia a Geometria Diferencial. Intuitivamente, várias superfícies, podem ser
entendidas como lâminas delgadas assumindo formas variadas; entretanto, o assunto é tão
complexo que na Geometria Diferencial o conceito de superfície é estendido a objetos que
estão além da percepção humana.
SUPERFÍCIE E CURVA
Já se tem exemplo de um tipo de superfície que é a superfície plana, simplesmente
chamada de plano e estudado em Matemática III; considerou-se o plano, como também a
reta e as cônicas, uma noção geométrica que se entende baseado na intuição e assim se tem
a sua aceitação; a Geometria Analítica permitiu estabelecer uma equivalência entre as
noções geométricas (de reta, das cônicas e do plano) e certas equações, tal equivalência
permitiu obter as noções geométricas usando as equações e utilizar as equações para
estabelecer as noções geométricas; tal sistemática continuará sendo usada para estabelecer
outros exemplos de superfícies.
Uma superfície plana é sempre dada pela equação de primeiro grau
ax + by + cz + d = 0 e reciprocamente. Indicando F(x, y, z) como uma expressão que
depende de x, y e z, diz-se que
F(x, y, z) = 0
é uma equação das três variáveis x, y e z. Logo, pode-se dizer que todo plano é dado por
uma equação de três variáveis, isto é, todo ponto (x, y, z) de um plano é solução de uma
equação do tipo F(x, y, z) = 0; mas F(x, y, z) = 0 pode representar uma figura não
necessariamente plana, mais do que isto, existem equações de três variáveis que: não têm
nenhuma solução, por exemplo, x 2 + y 2 + z 2 + 1 = 0; têm somente uma solução, por
exemplo, x 2 + y 2 + z 2 = 0 em que apenas (0, 0, 0) é solução; define um único plano, por
exemplo, (x − y + z) 2 = 0 que é equivalente a
x − y + z = 0; representa dois planos, por
2 SUPERFÍCIE E CURVA
exemplo, x 2 − y 2 = 0
que é equivalente a
x−y=0
ou
x + y = 0. A equação
x 2 + y 2 + z 2 − 1 = 0, é um exemplo onde o conjunto das soluções tem uma infinidade de
pontos (x, y, z), mas esse conjunto de pontos não representa nenhum plano.
O certo e que será visto a seguir, é que existem vários exemplos de superfícies que
são equivalentes a equações do tipo F(x, y, z) = 0; neste caso, diz-se que a superfície é o
conjunto das soluções (x, y, z) de F(x, y, z) = 0, a figura ou lugar geométrico determinado
pelas representações geométricas das soluções no sistema cartesiano XYZ; tal figura ou
lugar geométrico é também dito o gráfico da equação.
A Geometria Analítica trata somente da superfície plana e outras que podem ser
dadas pela equação
ax 2 + by 2 + cz 2 + dxy + exz + fyz + gx + hy + iz + j = 0
onde os coeficientes a, b, ..., f não são todos nulos, chamada de equação de segundo grau
em x, y e z. Observe que se os coeficientes a, b, ..., f forem todos nulos, a equação é de
primeiro grau. Dos exemplos anteriores, observa-se que nem toda equação de segundo grau
define um conjunto que a intuição possa aceitar como uma superfície, pois o conjunto das
soluções da equação pode ser vazio ou apenas um ponto; além disso, como também foi
visto, existem casos em que pode definir um plano ou um par de planos. Os conjuntos das
soluções da equação de segundo grau, são classificados como degenerados se o conjunto
é vazio, unitário, um plano ou um par de planos, e não degenerados nos outros casos; os
conjuntos não degenerados (ou as figuras representadas pelos conjuntos no sistema
cartesiano), são também chamados de superfícies quádricas. É possível mostrar que
existem, além das chamadas superfícies cilíndricas, um total de seis superfícies quádricas
que são chamadas de: elipsóide, cone elíptico, parabolóide elíptico, hiperbolóides elípticos
de uma e duas folhas, e parabolóide hiperbólico.
Foi visto em Matemática III que a interseção de dois planos transversais é uma reta
no espaço cartesiano. Em geral, duas superfícies dadas por F(x, y, z) = 0 e G(x, y, z) = 0,
podem se interceptar definindo uma curva C no espaço cartesiano, neste caso, C é o
conjunto de todos os pontos que satisfazem simultaneamente as duas equações, isto é,
C = {(x, y, z) ∈ R 3; F(x, y, z) = 0 e G(x, y, z) = 0}.
A curva C pode ainda ser interpreta como o conjunto de todas as soluções do sistema
formado pelas duas equações F(x, y, z) = 0 e G(x, y, z) = 0, e também se indica na forma
abreviada
{
C F(x, y, z) = 0 .
G(x, y, z) = 0
SUPERFÍCIE E CURVA 3
Os métodos da Geometria Analítica consistem em estudar as superfícies quádricas
particularmente posicionadas em relação ao sistema de coordenadas, a partir daí usando
translação e rotação de eixos, analisar a equação de segundo grau para concluir que ela
define apenas superfícies das formas já estudadas se o conjunto das soluções não for
degenerado. O estudo de rotação de eixos, será omitido por ser desnecessário para os
objetivos deste texto; desta forma, este texto não poderá chegar na classificação
mencionada para a equação de segundo grau. Tal classificação pode ser encontrada na
referência “Elementos de Geometria Analítica, Nikolai Efimov – Livraria Cultura
Brasileira Editora, São Paulo, 1972.
SUPERFÍCIE CILÍNDRICA
Sejam uma curva C e uma reta r do R 3, o conjunto de pontos S do R 3 obtido
pela reunião de todas as retas paralelas a r e contendo algum ponto de C, é dito uma
superfícies cilíndrica ou apenas um cilindro. Sendo assim, uma superfície cilíndrica pode
ainda ser interpretada como o subconjunto gerado por uma reta que se desloca
paralelamente a r e ao longo de C. A curva é chamada de diretriz do cilindro e cada uma
das retas paralelas a r é dita uma geratriz do cilindro.
C
( di
r
e tr iz )
S
)
riz
rat
(ge
r
Se a diretriz de uma superfície cilíndrica é uma curva C contida no plano XY e
g(x, y, z) = 0
(isto é, C é a interseção de uma
geratrizes paralelas ao eixo Z, então C
z=0
superfície g(x, y, z) = 0 com o plano z = 0) e e3 = (0, 0,1) é um vetor diretor do eixo Z.
{
4 SUPERFÍCIE E CURVA
Um ponto Q(x, y, z) ∈ S se, e somente se, existem P ( x o , yo , 0 ) ∈ C e t ∈ R tal que
PQ = te3.
Z
Q
S
O
A figura ilustra a superfície cilíndrica
S, a diretriz C e uma geratriz l de S, e
o vetor de P até Q.
Y
P
l
C
X
PQ = te3, tem-se
x o = x, yo = y e z = t; como
P ∈ C, obtém-se
g ( x o, yo, 0 ) = 0 e z ∈ R, ou seja, g(x, y, 0) = 0 e z ∈ R, isto significa que todo ponto
(x, y, z) ∈ S satisfaz uma equação que não depende de z e z ∈ R; logo, tal superfície
cilíndrica é dada por uma equação do tipo f (x, y) = 0. Suponha agora que uma equação do
tipo f (x, y) = 0 define uma superfície S e seja Q ( x o, yo, z o ) ∈ S, então f ( x o , yo ) = 0
para qualquer z ∈ R, daí S contém o conjunto {( x o, yo, z ) ; z ∈ R} que é uma reta
paralela ao eixo Z; isto mostra que S é constituída de retas paralelas ao eixo Z, ou seja, S
é cilíndrica.
Sendo
Portanto, um conjunto S de pontos do R 3, é uma superfície cilíndrica de
geratrizes paralelas ao:
(a) Eixo Z se, e somente se, S é dada por uma equação do tipo f (x, y) = 0; sendo assim,
f (x, y) = 0
qualquer curva D
onde k é uma constante, é uma diretriz de S;
z=k
f (x, y) = 0
é a diretriz de S no plano XY e é a projeção de
particularmente, C
z=0
qualquer diretriz de S no plano XY.
{
{
Z
D
l
z=
k
O
Y
A figura ilustra uma superfície S,
as diretrizes C no plano z = 0 e D
no plano z = k.
C
X
S
Analogamente, pode-se enunciar que um conjunto S de pontos do R 3, é uma
superfície cilíndrica de geratrizes paralelas ao:
SUPERFÍCIE E CURVA 5
(b) Eixo X se, e somente se, S é dada por uma equação do tipo g(y, z) = 0; sendo assim,
g(y, z) = 0
qualquer curva D
onde k é uma constante, é uma diretriz de S;
x=k
g(y, z) = 0
particularmente, C
é a diretriz de S no plano YZ e é a projeção de
x=0
qualquer diretriz de S no plano YZ;
(c) Eixo Y se, e somente se, S é dada por uma equação do tipo h(x, z) = 0; desta forma,
h(x, z) = 0
qualquer curva D
onde k é uma constante, é uma diretriz de S;
y=k
h(x, z) = 0
é a diretriz de S no plano XZ e é a projeção de
particularmente, C
y=0
qualquer diretriz de S no plano XZ.
{
{
{
{
Como pode ser observado de (a) até (c), uma superfície cilíndrica de geratrizes
paralelas a um dos eixos coordenados, é definida por uma equação que independe de uma
das variáveis do sistema, tal variável é precisamente aquela relativa ao eixo coordenado em
que as geratrizes são paralelas.
Exemplo Resolvido 1. Verificar que a superfície dada pela equação indicada é cilíndrica,
achar a diretriz num plano coordenado e fazer o gráfico da equação: (a) x 2 + y 2 = 1;
(b) y − x 2 = 0.
Solução.
(a) Como x 2 + y 2 − 1 = 0 independe de z, tem-se uma superfície cilíndrica de
{
x 2 + y2 = 1
é a sua diretriz no plano XY.
z=0
Conforme foi visto em 0.5.5 do volume 1 (pág. 52), C é a circunferência de centro em
(0, 0, 0) e raio igual a 1. Traçando a diretriz e as retas paralelas ao eixo Z que contém
algum ponto de C, obtém-se o gráfico da equação na figura a seguir.
geratrizes paralelas ao eixo Z, assim
C
Z
S
l
O
Y
C
X
(b) A superfície dada por
{
y − x 2 = 0 é uma superfície cilíndrica de geratrizes
y = x2
é a sua diretriz no plano XY. Conforme foi visto em
z=0
0.5.6 do volume 1 (pág. 53), C é a parábola convexa de vértice em (0, 0, 0) e eixo no
paralelas ao eixo Z, assim C
6 SUPERFÍCIE E CURVA
eixo Y. Traçando a diretriz e as retas paralelas ao eixo Z que contém algum ponto de C,
obtém-se a figura a seguir.
Z
S
l
O
Y
C
X
Exemplo Proposto 1. Verificar que a superfície dada pela equação indicada é cilíndrica,
achar a diretriz num plano coordenado e fazer o gráfico da equação: (a) y 2 + z 2 = 1; (b)
x 2 + z 2 = 1; (c) y = x 2; (d) y = 1 − z 2; (e) xy = 1.
As superfícies cilíndricas com diretriz igual a uma circunferência e geratrizes
paralelas a um dos eixos coordenados, são chamadas de cilindro circular reto; o centro da
circunferência também é dito o centro do cilindro; a reta que contém o centro da
circunferência (ou o centro do cilindro) e é paralela as diretrizes é dita o eixo do cilindro.
Geometricamente, observe que a interseção de um cilindro circular reto com um plano:
(a) Paralelo ao eixo do cilindro, é uma ou duas retas:
(b) Transversal ao eixo do cilindro, é uma circunferência ou uma elipse, conforme o plano
e o eixo sejam perpendiculares ou não, respectivamente.
é a interseção das superfícies dadas por F(x, y, z) = 0 e
F(x, y, z) = 0
, obtém-se uma
G(x, y, z) = 0, então eliminando a variável z do sistema
G(x, y, z) = 0
equação do tipo f (x, y) = 0; caso f (x, y) = 0 defina uma superfície S, como foi visto, S é
cilíndrica de geratrizes paralelas ao eixo Z, além disso C ⊂ S e é uma diretriz de S, logo
f (x, y) = 0
C xy
é a projeção de C no plano XY.
z=0
Se uma curva
C
{
{
S
Z
C
C
SS2 1
S 12
O
X
Cxy
Y
A figura ilustra as
superfícies S 1 e S 2, a
curva C de interseção
de S 1 e S2 , a superfície
cilíndrica S e a projeção
Cxy de C no plano XY.
SUPERFÍCIE E CURVA 7
Similarmente, eliminando do sistema
F(x, y, z) = 0
, a variável x ou a variável
{G(x,
y, z) = 0
y, pode-se obter as projeções de C nos planos YZ ou XZ, respectivamente.
{
2
Exemplo Resolvido 2. Achar a projeção da curva C x + z = 1 no plano XY. Fazer os
y−z = 0
gráficos da projeção e da curva.
{
x 2 + z = 1 tem-se
y = 1 − x 2 que uma
,
y−z =0
superfície cilíndrica de geratrizes paralelas ao eixo Z e contendo C, logo a projeção de
y = 1− x2
C no plano XY é dada por
que é parábola indicada na figura a seguir.
z=0
Solução. Eliminando a variável z no sistema
{
Z
O
Y
X
Pode-se ter o gráfico da curva visualizando a interseção do cilindro x 2 + z = 1 com
o plano y − z = 0, ou ainda, visualizando os pontos do cilindro ou do plano cuja projeção
deu a parábola citada, obtendo-se a figura a seguir.
Exemplo Proposto 2. Mostrar que:
x2 + z = 1
y = x2 − x
no plano XY, é a parábola
(a) A projeção da curva
. Fazer o
x + y + z =1
z=0
gráfico da projeção e da curva;
(b) A curva de interseção dos cilindros x 2 + z 2 = 1 e x 2 + y 2 = 1 são elipses. Fazer os
gráficos das elipses e representar geometricamente a parte de um cilindro interno ao
outro.
{
{
8 SUPERFÍCIE E CURVA
SUPERFÍCIE DE REVOLUÇÃO
Sejam uma curva C e uma reta r contidas num plano. Considere também uma
circunferência contida num plano perpendicular a r, de centro num ponto de r e contendo
um ponto de C.
C
r
O conjunto de todas as circunferências é chamado de superfície de revolução. Sendo
assim, pode ser dito que uma superfície de revolução S é o conjunto dos pontos gerados
pela revolução de C em torno de r.
r
C
S
A reta r é chamada de eixo de revolução da curva C ou eixo da superfície de
revolução S e a curva C é dita uma geratriz da superfície de revolução S. A interseção
de S com qualquer plano contendo r, são duas geratrizes de S. A interseção de S com
qualquer plano perpendicular a r, é sempre uma circunferência chamada de seção plana
de S perpendicular a reta r.
Seja uma superfície de revolução S onde a geratriz é uma curva C contida no
plano YZ do espaço cartesiano e o eixo de revolução é o eixo Z, considere ainda
y = f (z)
C
(isto é, C é a interseção de uma superfície cilíndrica y − f(z) = 0 com o
x=0
{
SUPERFÍCIE E CURVA 9
plano x = 0). Se P(x, y, z) ∈ S, então P pertence a circunferência de centro em
Co ( 0, 0, z ) e raio igual a | yo | = f (z) onde Po ( 0, y o , z ) ∈ C.
Z
C
Co
Po (0,yo ,z)
P(x,y,z)
O
Y
X
x 2 + y 2 = y o2 e daí x 2 + y 2 = [ f (z)]2 ,
Sendo assim, tem-se CoP = CoPo , ou seja,
isto significa que todo ponto P(x, y, z) ∈ S satisfaz uma equação em que a soma dos
quadrados das variáveis x e y, é uma função não negativa de z. Observe que outras
geratrizes de S nos planos YZ e XZ podem ser obtidas, pois em x 2 + y 2 = [ f (z) ]2 ,
fazendo x = 0 dá
{xy == 0±f (z) e tomando
y = 0 dá
{xy == 0±f (z) . Suponha agora que uma
superfície S é dada pela equação x 2 + y 2 = p(z) onde p(z) ≥ 0 e contínua para todo z
num intervalo I, fazendo z = z o ∈ I, tem-se
{
x 2 + y 2 = p(z o ) que é uma circunferência
z = zo
no plano z = z o de centro em (0, 0, z o ) e raio igual a p ( z o ), isto mostra que toda seção
plana de S perpendicular ao eixo Z é uma circunferência, logo S é uma superfície de
revolução do tipo exemplificado.
Portanto, um conjunto S de pontos do R 3 é uma superfície de revolução com
uma geratriz contida no:
(a) Plano YZ ou XZ e tendo o eixo Z como eixo de revolução se, e somente se, S é dada
por uma equação do tipo x 2 + y 2 = [ f (z)]2 .
Z
O
Y
X
Analogamente, pode-se afirmar que um conjunto S de pontos do R 3
é uma
10 SUPERFÍCIE E CURVA
superfície de revolução tendo como eixo de revolução o:
(b) Eixo X se, e somente se, S é dada por uma equação do tipo y 2 + z 2 = [ g(x) ]2 ; sendo
assim,
as geratrizes nos planos XY
ou
XZ
são dadas por
{zy == ±0g(x) , respectivamente;
{zy == 0±g(x)
ou
(c) Eixo Y se, e somente se, S é dada por uma equação do tipo x 2 + z 2 = [ h(y)]2 ; desta
forma, as geratrizes nos planos XY ou YZ são as respectivas curvas
{zx == ±0h(y) .
{zx == 0±h(y) ou
Como pode ser observado de (a) até (c), uma superfície de revolução obtida pela
revolução de uma curva em torno de um dos eixos coordenados, é definida por uma
equação em que a soma dos quadrados de duas das três variáveis depende somente de uma
função não negativa da terceira variável; além disso, o eixo de revolução coincide com o
eixo coordenado correspondente a essa terceira variável.
Algumas superfícies de revolução recebem nomes especiais, tais superfícies são
chamadas:
(a) Esfera se for gerada por uma circunferência (ou uma semi-circunferência) em torno de
uma reta contendo um diâmetro da circunferência. O centro e raio da circunferência
são também ditos o centro e raio da esfera. Assim, sendo C e r, o centro e raio da
circunferência, respectivamente, pode ser dito que a esfera é o conjunto de todos os
pontos eqüidistantes r de C.
(b) Cone de revolução se for gerada pela revolução de uma reta em torno de outra reta
transversal. O ponto de interseção C das retas é dito o centro do cone.
SUPERFÍCIE E CURVA 11
r
C
C
(c) Parabolóide de revolução se for gerada pela revolução de uma parábola (ou uma
semi-parábola) em torno do seu eixo. O vértice V da parábola também é chamado de
vértice do parabolóide.
(d) Hiperbolóide de revolução se for gerado pela revolução de uma hipérbole, em torno da
reta no plano da hipérbole, perpendicular ao seu eixo e contendo o ponto médio dos
vértices da hipérbole ou em torno do eixo da hipérbole, tais casos são ditos
hiperbolóide de uma folha e hiperbolóide de duas folhas, respectivamente. O ponto
médio C dos vértices da hipérbole é chamado de centro do hiperbolóide.
Vale lembrar que a reta r (isto é, o eixo de revolução), em cada exemplo de
superfície, é o eixo da superfície. Assim, cada reta contendo o centro da esfera, é um eixo
da esfera.
12 SUPERFÍCIE E CURVA
Exemplo Resolvido 1. Encontrar a equação da esfera de centro em O(0, 0, 0) e raio igual
a r.
Solução. Como um ponto qualquer P(x, y, z) da esfera deve satisfazer d ( O, P ) = r, tem-
se
( x − 0 )2 + ( y − 0 )2 + ( z − 0 )2 = r, daí
x 2 + y2 + z 2 = r 2
é a equação da esfera.
Exemplo Proposto 1. Mostrar que a equação da esfera gerada pela revolução da
x 2 + y2 = r 2
em torno do eixo X ou eixo Y e da circunferência
circunferência
z=0
{
{
y2 + z 2 = r 2
em torno do eixo Y ou eixo Z, é dada por x 2 + y 2 + z 2 = r 2.
x=0
Exemplo Resolvido 2. Achar a equação do cone gerado pela revolução da reta
 y = m1 z

x = 0
em torno do eixo Z e fazer um esboço da superfície.
Solução. Pelo que foi visto, o cone é dado por x 2 + y 2 = ( m1 z ) , isto é, o cone é dado por
2
uma equação do tipo
=
seguir.
z2
m 2 x 2 + m 2 y 2,
z 2 = m 2 x 2 + m 2 y 2.
Para obter o gráfico da equação
basta traçar a reta e girar em torno do eixo Z e que está na figura a
Z
O
Y
X
Exemplo Proposto 2. Mostrar que a equação do cone gerado pela revolução de uma reta
contendo a origem, em torno do eixo indicado é como está dada e fazer o gráfico da
equação:
(a) Eixo X e x 2 = ay 2 + az 2 onde a > 0;
(b) Eixo Y e y 2 = ax 2 + az 2 onde a > 0.
Exemplo Resolvido 3. Determinar a equação do parabolóide gerado pela revolução da
SUPERFÍCIE E CURVA 13
parábola
{
z = ay 2
(a > 0) em torno do eixo Z e fazer o gráfico da equação.
x=0
Solução. Para obter o parabolóide, basta girar em torno do eixo Z a semi-parábola à direita
do eixo Z e fazendo y em função de z na equação
z = ay 2; sendo assim, a semi2
y = 1 z
z
a , logo a equação do parabolóide é x 2 + y 2 =
, ou
parábola é dada por 
a
x = 0
seja, o parabolóide é dado por uma equação do tipo z = ax 2 + ay 2. Girando a parábola em
( )
torno do eixo Z, tem-se o gráfico da equação z = ax 2 + ay 2 na figura a seguir.
Z
O
Y
X
Exemplo Proposto 3. Mostrar que a equação do parabolóide gerado pela revolução da
parábola em torno do eixo indicado, é como está dada e fazer o gráfico da equação:
2
2
(b) y = az e eixo Y, y = ax 2 + az 2.
(a) x = az e eixo X, x = ay 2 + az 2;
y=0
x=0
{
{
Exemplo Resolvido 4. Calcular a equação do hiperbolóide de uma folha e de duas folhas
 y 2 − z 2 = 1
− y 2 + z2 = 1
gerados pela rotação das hipérboles  a 2 b2
e  a 2 b2
em torno do eixo Z.
 x = 0
 x = 0
Fazer os gráficos das equações.
Solução. Para calcular a equação do hiperbolóide de uma folha, basta girar em torno do
eixo Z o ramo da hipérbole à direita do eixo Z e fazendo y como função de z na
2

z2
2
equação y 2 − z 2 = 1; sendo assim, o ramo é dado por  y = a 1 + b 2 , logo a equação do
a
b
 x = 0
(
2
hiperbolóide é x 2 + y 2 = a 1 + z 2
equação do tipo
x2
a2
2
b
) , isto é, o hiperbolóide de uma folha é dado por uma
2
+ y2 − z 2 = 1.
a
2
b
A fim de achar a equação do hiperbolóide de duas folhas, basta girar em torno do
eixo Z os semi-ramos da hipérbole à direita ao eixo Z e fazendo y como função de z na
14 SUPERFÍCIE E CURVA
2
equação − y 2 + z 2 = 1;
2
a
b
onde z < −b ou

desta forma, as partes dos ramos são dados por  y = a
 x = 0
(
z > b, portanto a equação do hiperbolóide é x 2 + y 2 = a
z2
b2
2
2
seja, o hiperbolóide de duas folhas é dado por uma equação do tipo
−
x2
a2
−
y2
b2
+
z2
b2
x2
a2
)
−1
2
− 1 , ou
+ y2 − z 2 = −1 ou
b
b
= 1.
 y = a 1 + z2
b2

 x = 0
Girando as curvas
equações
x2
a2
z2
b2
2
2
 y = a

 x = 0
e
z2
b2
− 1 , tem-se os gráficos das
+ y2 − z 2 = 1 e − x2 − y2 + z 2 = 1, nas respectivas figuras a seguir.
a
2
2
b
a
b
2
b
Z
Z
O
Y
O
Y
X
X
Exemplo Proposto 4. Mostrar que as equações dos hiperbolóides de uma folha e duas
 y 2 z2
folhas gerados pela revolução da hipérbole − a 2 + b2 = 1 em torno do eixo Y e em torno
 x = 0
do eixo Z, são dadas por
x2
b2
2
2
− y2 + z 2 = 1 e − x2 − y2 + z 2 = 1, respectivamente. Fazer os
a
2
b
2
a
a
2
b
gráficos das equações.
Geometricamente, observe que a interseção de um cone com um plano, pode ser
apenas uma ou duas retas, ou ainda uma das cônicas (isto é, uma circunferência, uma
elipse, uma parábola ou uma hipérbole, conforme foram vistas em 0.5.5 a 0.5.8 do
volume 1), onde é obtida uma:
(a) Reta se o plano contém somente uma geratriz do cone e duas retas se o plano contém o
eixo do cone;
(b) Circunferência se o plano for normal ao eixo do cone e não contém o centro do cone;
(c) Elipse se o plano for transversal ao eixo do cone, não for normal ao eixo e nem contém
o centro do cone;
(d) Hipérbole se o plano for paralelo ao eixo do cone e não contém o eixo.
Exemplo Resolvido 5. Usando a equação do cone do exemplo resolvido 2 de superfícies
SUPERFÍCIE E CURVA 15
de revolução, encontrar uma reta, duas retas e uma circunferência como interseção do cone
com o plano.
Solução. Para achar uma única reta, basta tomar a interseção do cone z 2 = m 2x 2 + m 2 y 2
z = my
com o plano z = my obtidos no exemplo resolvido 2, assim a reta é dada por
x=0
{
onde a equação x = 0 é obtida do sistema
{
z 2 = m2x 2 + m 2 y2
pela eliminação de z.
z = my
Para determinar duas retas, basta tomar a interseção do cone z 2 = m 2x 2 + m 2 y 2
z = ±my
onde as equações z = ±my
com o plano x = 0, assim as retas são dadas por
x=0
{
são obtidas do sistema
z2
{zx ==0m x + m y
2
2 2
2 2
pela eliminação de x.
Para encontrar uma circunferência, considera-se a interseção do cone
com o plano z = k (k ≠ 0), assim a circunferência é dada por
= m 2x 2 + m 2 y 2
2
x 2 + y 2 = ( mk )
onde a equação
z = k
z 2 = m2x 2 + m 2 y2
pela eliminação de z.
z=k
2
x 2 + y 2 = ( mk )
é obtida do sistema
{
Exemplo Proposto 5. Usando o cone do exemplo resolvido 2 de superfícies de revolução,
achar uma elipse e uma hipérbole como interseções do cone com planos.
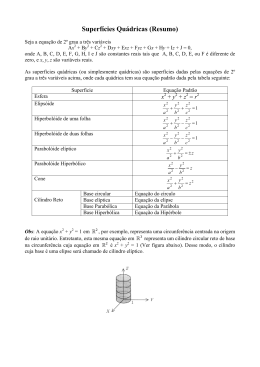
SUPERFÍCIES QUÁDRICAS
Como foi visto em superfícies de revolução, qualquer seção plana de uma
superfície de revolução perpendicular ao eixo de revolução, é uma circunferência; essa
característica da superfície de revolução, é suficiente para reconhecer se uma equação
F(x, y, z) = 0 define uma superfície de revolução, a partir de tal identificação fica fácil
obter a forma da superfície girando uma geratriz da superfície. Em geral, a interseção de
uma superfície com um plano perpendicular a uma reta, é chamada de seção plana da
superfície perpendicular à reta. Várias superfícies dadas através de equações, podem ter a
sua forma determinada reconhecendo algumas ou alguns grupos de seções planas da
superfície, essa sistemática é chamada de método das seções planas para identificar a
superfície ou fazer o gráfico da equação.
As superfícies quádricas foram classificadas no início deste texto e a superfície
cilíndrica já foi estudada, as equações das superfícies quádricas restantes seguidas dos
nomes são estabelecidas a seguir, vale observar que as superfícies de (a) até (e) poderão
16 SUPERFÍCIE E CURVA
ser de revolução, dependendo da igualdade dos parâmetros a, b ou c:
2
2
y2
(a) x 2 + 2 + z 2 = 1
a
b
c
X, Y e Z).
(Elipsóide de centro na origem e eixos contidos nos eixos
 y2 z2
A interseção do elipsóide com o plano YZ, é a elipse  b2 + c2 = 1. Cada seção
x = 0
z2
 x 2 y2
plana do elipsóide perpendicular ao eixo Z, dada por  a 2 + b2 = 1 − c2 com −c < k < c, é
z = k
uma elipse e sendo z = ±c tem-se os pontos (0, 0, ±c). Logo, o elipsóide tem a forma
indicada na figura a seguir.
2
2
2
2
y2
y2
(b) z 2 = x 2 + 2 , x 2 = 2 + z 2 e y 2 = x 2 + z 2
(Cones elípticos de centros na
a
b
a
b
a
b
origem e eixos iguais aos eixos Z, X e Y, respectivamente).
2
y2
Por exemplo, o cone elíptico dado por z 2 = x 2 + 2 , a interseção do cone elíptico
a
b
y

com o plano YZ, são as retas  z = ± b . Cada seção plana do cone elíptico perpendicular ao
x = 0
2
 x 2 y2
eixo Z, dada por  a 2 + b 2 = k para k ≠ 0, é uma elipse e sendo k = 0 obtém-se o
z = k
ponto (0, 0, 0). Logo, o cone elíptico tem a forma indicada na figura seguinte.
Z
O
X
Y
SUPERFÍCIE E CURVA 17
2
2
2
2
y2
y2
(c) ±z = x 2 + 2 , ±x = 2 + z 2 e ± y = x 2 + z 2
(Parabolóides elípticos de vértices
a
b
a
b
a
b
na origem e eixos iguais aos eixos Z, X e Y, respectivamente).
2
2
2
2
y2
y2
x 2 − y2 − z2 = 1
(d) x 2 + 2 − z 2 = 1, − x2 + 2 + z2 = 1
e
(Hiperbolóides
a
b
c
a
b
c
a 2 b 2 c2
elípticos de uma folha de centros na origem e eixos iguais aos eixos Z, X e Y,
respectivamente).
2
2
2
2
2
2
y2
y2
y2
(e) − x2 − 2 + z 2 = 1, x 2 − 2 − z2 = 1 e − x2 + 2 − z2 = 1 (Hiperbolóides elípticos
a
b
c
a
b
c
a
b
c
de duas folhas de centros na origem e eixos iguais aos eixos Z, X e Y,
respectivamente).
Z
Z
O
Y
Y
O
X
X
2
( ax
2
+
y2 z2
- =1
b2 c2
y2
2
( - ax
)
2
2
2
- y2 + z2 = 1
b
c
)
2
2
2
2
y2
(f) ±z = − x 2 + 2 , ± y = x 2 − z 2 e ±x = − 2 + z 2 (Parabolóides hiperbólicos de
a
b
a
b
a
b
centros na origem e simétricos em relação aos planos YZ, XY e XZ,
respectivamente).
2
Por exemplo, o parabolóide hiperbólico S dado por z = − x2 + y2 , a interseção de
2
a
b

S com o plano YZ é a parábola convexa z =
e com cada plano y = k é a parábola
x = 0
x2 k2
2

da parábola convexa.
côncava  z = − a 2 + b 2 que tem vértice no ponto
0, k, k 2
b
=
y
k

Considere agora a interseção de S com os planos z = k, então se: z = k > 0, tem-se a
y2
b2
(
)
 x 2 y2
hipérbole  − a 2 + b 2 = k com eixo paralelo ao eixo Y e vértices nos pontos 0, ±b k, k
z = k
y2
b

da parábola convexa z = b2 ; z = k = 0, obtém-se as retas y = ± a x ; z = k < 0, tem-se a
z=0
x = 0
(
)
{
 x 2 y2
hipérbole  a 2 − b 2 = −k com eixo paralelo ao eixo X e vértices nos pontos
z = k
( ±a
−k, 0, k
)
18 SUPERFÍCIE E CURVA
2
x2 y

da parábola côncava  z = − a 2 + b2 . Logo, o parabolóide hiperbólico tem a forma indicada
y = 0
na figura seguinte.
Uma superfície diz-se regrada se ela é formada de retas. Dentre os exemplos de
superfícies estudadas, ficou evidente que algumas são desse tipo, como por exemplo:
plano, cilindro e cone. Embora não seja aparente, o hiperbolóide de uma folha e o
parabolóide hiperbólico também são superfícies regradas.
Exemplo Resolvido. Mostrar que o hiperbolóide de uma folha dado no item (d) é uma
superfície regrada.
Solução. Por exemplo, se o hiperbolóide é dado por
x2
a2
2
− z2 = 1 − y2 , ou seja,
2
c
b
( xa − zc )( xa + zc ) = (1 − by )(1 + by ) .
rmn
x2
a2
2
+ y2 − z2 = 1,
b
2
c
então
Seja a reta dada por
( xa + zc ) = n (1 − by )
( xa − zc ) = m (1 + by )
m


n

onde m e n não são simultaneamente nulos, se P(x, y, z) satisfaz o sistema de rmn
(isto é, se P ∈ rmn ), então P satisfaz a equação de S, logo rmn ⊂ S. Para concluir que S
é formada de retas, basta mostrar que cada ponto de S está contido em alguma reta rmn ,
isto é, sendo Q ( x o, yo, z o ) ∈ S, deve-se mostrar que existem m e n tais que Q ∈ rmn. Se
Q ∈ S, então
 x o z o   x o z o   yo  yo 
 a − c   a + c  = 1 − b  1 + b  .


 


Observe que
SUPERFÍCIE E CURVA 19
Q ∈ rmn
então: sendo 1 −
yo
b
  x o zo 
 yo 
m  a + c  = n  1 − b 
⇔
,
x
z
y
n  o − o  = m 1 + o 
c 
b 
  a

≠ 0, tem-se n = k om onde k o =
x o zo
+
a c
y
1− o
b
, logo (substituindo n no
sistema que define rmn )
(
( )
( ) ( )
)
m x + z = mk 1 − y
o
 a c
b
, ou seja,

y
x
z
mk o − = m 1 +
a c
b

( )
 x + z = k 1− y
o
a c
b se m ≠ 0,

x
z
k o − = 1 + y

a c
b
(
)
este último sistema define uma reta r ⊂ S tal que Q ∈ r; se 1 −
então 1 +
yo
b
= 2 e assim m = k on onde
yo
b
= 0 (isto é, se
yo
b
= 1),
z 
x
k o = 12  o − o  , logo (substituindo m no
a
c 

sistema que define rmn )
(
) ( )
k n x + z = n 1 − y
 o a c
b , ou seja,
 x z
y
 n − = k on 1 +
a
c
b

(
)
( )
(
)
k x + z = 1 − y
 o a c
b
x z
y se n ≠ 0,
 − = ko 1 +
b
a c
( )
este último sistema também define uma reta s ⊂ S tal que Q ∈ s.
Exemplo Proposto. Mostrar que o parabolóide hiperbólico dado no item (f) é uma
superfície regrada.
TRANSLAÇÃO DE EIXOS
Sejam dois sistemas cartesianos XYZ e XYZ, de forma que os eixos
coordenados de um sistema tenham as mesmas orientações dos respectivos eixos
coordenados de outro sistema, neste caso, diz-se que um sistema é a translação do outro.
É de interesse posicionar um sistema em relação à posição do outro, assim considere que o
sistema XYZ está posicionado em relação ao sistema XYZ, isto é, que O(0, 0, 0) é a
origem do sistema XYZ e O ( x o, yo , z o ) é a origem do sistema XYZ, isto significa que
a origem do sistema XYZ está localizada no ponto
( x o, yo , z o )
do sistema XYZ.
Suponha que um mesmo ponto em relação aos sistemas XYZ e XYZ, sejam indicados
20 SUPERFÍCIE E CURVA
por
P(x, y, z) e P(x, y, z),
respectivamente. O objetivo é achar as relações entre as
coordenadas de P e P.
Sendo assim, tem-se OP = OO + OP; como OP = OP, obtém-se OP = OO + OP; mas
OP = (x, y, z), OO = ( x o, yo, z o ) e OP = (x, y, z), logo (da igualdade vetorial)
x = x − xo , y = y − y o e z = z − z o .
Tais relações são chamadas fórmulas de mudança de coordenadas da translação de
eixos.
Algumas equações de segundo grau mais gerais que as estudadas em superfícies
quádricas, podem ser reduzidas às já estudadas mediante mudança de coordenadas; neste
caso, os gráficos das equações mais gerais podem ser obtidos a partir dos gráficos nos
casos particulares.
Exemplo Resolvido 1. Fazer o gráfico da equação dada:
(a) x 2 + y 2 − 2x + 2y + 1 = 0;
(b) x 2 − 2x + y − 3 = 0.
Solução.
(a) Completando
os
2
2
x + y − 2x + 2y + 1 = 0, tem-se
quadrados
em
x
e
y
na
equação
(x − 1)2 + (y − 1)2 = 1;
assim fazendo x = x − 1, y = y + 1 e z = z, obtém-se
x 2 + y2 = 1
que define uma superfície cilíndrica no sistema XYZ. Observe que a origem deste
sistema é O(1, −1, 0) em relação ao sistema XYZ. Colocando os dois sistemas e fazendo
o gráfico de x 2 + y 2 = 1 (de acordo como foi obtido no exemplo resolvido 1 de
superfície cilíndrica), obtém-se o gráfico da equação dada.
SUPERFÍCIE E CURVA 21
Z
Z
-1
O
O
O
Y
Y
1
X
X
(b) Completando o quadrado em
x
na equação
x 2 − 2x + y − 3 = 0, tem-se
y − 2 − (x + 1) 2 = 0; logo, tomando x = x + 1, y = y − 2 e z = z, acha-se
y − x2 = 0
que define uma superfície cilíndrica no sistema XYZ. A origem deste sistema é
O(−1, 2, 0) em relação ao sistema XYZ. Colocando os dois sistemas e fazendo o gráfico
de y − x 2 = 0 (de acordo como foi obtido no exemplo resolvido 1 de superfície
cilíndrica), obtém-se o gráfico da equação dada.
Z
Z
S
O
O
X
C
Y
Y
X
Exemplo Proposto 1. Fazer o gráfico da equação dada:
(b) xy + x − y = 2.
(a) x 2 + z 2 − 4x − 4z + 7 = 0;
Observe nos exemplos que é desnecessário introduzir os eixos do sistema XYZ
para obter as figuras, basta fazer uma diretriz e identificar a direção da geratriz. Por
exemplo, no exemplo resolvido 1(a), a superfície é cilíndrica pois a equação
x 2 + y 2 − 2x + 2y + 1 = 0
independe de z, logo uma diretriz é a circunferência
22 SUPERFÍCIE E CURVA
{
(x − 1)2 + (y + 1)2 = 1
e as geratrizes são paralelas ao eixo Z, assim fazendo a
z=0
circunferência de centro em (1, −1, 0) e raio igual a 1 no plano XY, depois gerando a
figura usando retas paralelas ao eixo Z, obtém-se o gráfico de x 2 + y 2 − 2x + 2y + 1 = 0. A
sistemática usada no exemplo resolvido 1 para fazer os gráficos das equações, pode
também ser utilizada, sempre que uma equação de segundo grau se reduza em algum outro
sistema às equações de (a) até (f) de superfícies quádricas, mas precisamente, quando a
equação de segundo grau pode ser escrita nas seguintes formas:
(a)
( x − x o ) 2 + ( y − y o )2 + ( z − z o ) 2 = 1
(b) ( z − z o )
2
2
2
x − x o ) ( y − yo )
(
=
+
a2
paralelo ao eixo Z);
(c) z − zo =
b2
( x − x o ) 2 + ( y − yo ) 2
a2
b2
eixo paralelo ao eixo Z);
(d)
(Elipsóide de centro em (xo , y o , z o ) e eixos
a2
b2
c2
paralelos aos eixos coordenados);
(Cone elíptico de centro em (xo , y o , z o ) e eixo
(Parabolóide elíptico de vértice em (xo , y o , z o ) e
( x − x o )2 + ( y − yo )2 − ( z − z o )2 = 1
(Hiperbolóide elíptico de uma folha de centro
a2
b2
c2
em (xo , y o , z o ) e eixo paralelo ao eixo Z);
(e) −
( x − x o ) 2 − ( y − y o ) 2 + ( z − z o )2 = 1
(Hiperbolóide elíptico de duas folhas de
a2
b2
c2
centro em (xo , y o , z o ) e eixo paralelo ao eixo Z);
(f) z − z o = −
( x − x o )2 + ( y − yo )2
(Parabolóide hiperbólico de centro em (xo , y o , z o )
a2
b2
e simétrico em relação ao plano x = xo ).
Para fazer o gráfico de qualquer equação particular de (a) até (f), basta usar o
procedimento sugerido após o exemplo proposto 1, isto é, não é necessário representar o
sistema XYZ, basta identificar a figura definida pela equação e obter informações para
localizar a figura no sistema XYZ, tais informações da figura podem ser: o centro ou
vértice e eixo(s), interseções com planos paralelos aos planos coordenados e contendo o
centro, pontos de interseções com o(s) eixo(s), seções planas perpendiculares ao(s) eixo(s),
etc.
Exemplo Resolvido 2. Fazer o gráfico da equação dada:
SUPERFÍCIE E CURVA 23
(a) 36x 2 + 9y 2 + 4z 2 − 72x − 36y + 8z + 40 = 0;
(b) 4x 2 + 9y 2 − 36z 2 + 16x − 36y + 144z + 92 = 0;
(c) −9x 2 − 4y 2 + 36z 2 + 18x + 16y − 144z + 83 = 0.
Solução.
(a) Completando os quadrados em
36(x − 1) 2 + 9(y − 2)2 + 4(z + 1)2 = 36, isto é,
x, y
e
z
na equação dada, obtém-se
(x − 1)2 (y − 2)2 (z + 1)2
+
+
= 1.
9
4
12
Esta última equação define (de acordo com o item (a) da relação de superfícies desta
seção) um elipsóide de centro em (1, 2, −1) e eixos paralelos aos eixos coordenados. As
interseções do elipsóide com os planos x = 1, y = 2 e z = −1, são as elipses
 (y−2)2 + (z+1)2 = 1 (x − 1)2 + (z +1)2 = 1
4
4
, 
 9
x = 1
y = 2
e
(x − 1)2 + (y−2)2 = 1
9
, respectivamente.

 z = −1
As
2
(k +1)2
2 (y − 2)

seções planas do elipsóide normais ao eixo Z, são as elipses (x − 1) + 9 = 1 − 4
z = k
onde −3 ≤ k ≤ 1. Localizando o centro do elipsóide (que também é o centro das três
elipses mencionadas inicialmente) e traçando as elipses, obtém-se o gráfico da equação na
figura a seguir.
Z
O
Y
X
(b) Completando os quadrados em
36(z − 2) 2 = 4(x + 2) 2 + 9(y − 2)2, ou seja,
(z − 2) 2 =
x, y e
z
na equação dada, obtém-se
(x + 2)2 (y − 2)2
.
+
9
4
Esta última equação define (de acordo com o item (b) da relação de superfícies desta
seção) um cone de centro em (−2, 2, 2) e eixo paralelo ao eixo Z. As interseções do cone
z = 12 y + 1
z = − 12 y + 3
e
com os planos x = −2 e y = 2, são as retas
, e


 x = −2
 x = −2
24 SUPERFÍCIE E CURVA
z = 13 y + 83
z = − 13 y + 43
e 
, respectivamente. As seções planas do cone perpendiculares

y = 2
y = 2
(x + 2) 2 (y − 2) 2
2

ao eixo Z, são as elipses (k − 2) = 9 + 4 . Localizando o centro do cone (que
z = k
também é a interseção das retas) e traçando as elipses, obtém-se o gráfico da equação na
figura a seguir.
Z
O
Y
X
(c) Completando os quadrados em x, y
−9(x − 1)2 − 4(y − 2) 2 + 36(z − 2)2 = 36, isto é,
−
e
z
na equação dada, obtém-se
(x − 1)2 (y − 2)2 (z − 2)2
−
+
= 1.
4
9
12
Esta última equação define (de acordo com o item (e) da relação de superfícies desta
seção) um hiperbolóide elíptico de duas folhas de centro em (1, 2, 2) e eixo paralelo ao
eixo Z. As interseções do hiperbolóide com os planos x = 1 e y = 2, são as hipérboles
− (y−2)2 + (z − 2)2 = 1
9
e

x = 1
− (x −1)2 + (z − 2)2 = 1
4
, respectivamente. As seções planas do

y = 2
 (x −1)2 + (y −2)2 = −1 + (k − 2) 2
9
hiperbolóide perpendiculares ao eixo Z, são as elipses  4
z = k
onde k ≤ 1 e k ≥ 3. Localizando o centro do hiperbolóide (que é o ponto médio dos
vértices das duas primeiras hipérboles mencionadas) e traçando as elipses, obtém-se o
gráfico da equação na figura a seguir.
Z
O
X
Y
SUPERFÍCIE E CURVA 25
Exemplo Proposto 2. Fazer o gráfico da equação dada:
(a) 4x 2 + 9y 2 − 16x − 36y − 36z + 16 = 0;
(b) 9x 2 + 36y 2 − 4z 2 − 36x − 144y + 8z + 140 = 0;
(c) 9x 2 − 4y 2 − 36x + 16y − 36z + 56 = 0.