Noções da Teoria dos Grafos
André Arbex Hallack
Junho/2015
Índice
1 Introdução e definições básicas.
Passeios eulerianos
1
2 Ciclos hamiltonianos
5
3 Árvores
7
4 Emparelhamento em grafos
11
5 Grafos planares:
Colorindo grafos e mapas
13
Referências
17
i
Capı́tulo 1
Introdução e definições básicas.
Passeios eulerianos
Introdução histórica
O Problema das pontes de Königsberg
Na cidade de Königsberg, sete pontes cruzam o rio Pregel, estabelecendo ligações entre duas ilhas
e entre as ilhas e as margens opostas do rio, conforme a ilustração abaixo:
Problema: É possı́vel fazer um “passeio” pela cidade, cruzando cada ponte exatamente uma vez?
Em 1736, Euler publicou um artigo demonstrando que tal passeio é impossı́vel. Mais importante
é o fato de Euler ter formulado um critério geral para resolver o problema acima, o que é considerado
como o primeiro teorema da chamada TEORIA DOS GRAFOS, a qual possui desdobramentos e
aplicações nas mais diversas áreas.
1
2
CAPÍTULO 1
Definição 1.1. Um GRAFO é uma coleção G = (N, A) constituı́da por um conjunto não-vazio e
finito N de NÓS (ou pontos, ou vértices) e um conjunto A de ARCOS (ou arestas), sendo que cada
arco liga dois nós (não necessariamente distintos).
Exemplos:
Um grafo é dito SIMPLES quando cada par de nós é ligado por no máximo um arco e nenhum
nó é ligado a si próprio (nenhum laço). Caso contrário, temos o chamado MULTIGRAFO.
Um arco é dito INCIDENTE nos nós aos quais está associado e vice-versa.
Um nó é dito ISOLADO quando não está ligado a nenhum outro.
Dois arcos incidentes num mesmo nó são ditos ADJACENTES. Dois nós incidentes num mesmo
arco são ditos adjacentes.
O GRAU de um nó é o número de arcos incidentes no nó, sendo que cada laço conta como dois
arcos.
Teorema 1.2. (Euler) A soma dos graus dos nós de um grafo é igual ao dobro do número de arcos.
Prova: Ao somarmos os graus contamos cada arco duas vezes, uma vez em cada extremidade.
Corolário 1. O número de nós de grau ı́mpar de todo grafo é sempre par.
De fato, se denotarmos por di o grau de cada nó i no grafo G = (N, A) , temos:
X
X
X
2 · #A =
di =
di +
di
i∈ IN
di par
X
X di ı́mpar
Como 2 · #A e
di são pares, então
di é par e para que a soma de números
di par
di ı́mpar
ı́mpares seja par, devemos ter uma quantidade par de números ı́mpares.
Exercı́cio: Prove que numa festa com 51 pessoas existe sempre uma pessoa que conhece um
número par de outras pessoas.
Introdução e definições básicas.
Passeios eulerianos
3
Passeios eulerianos
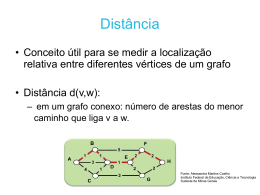
Definição 1.3. Um PASSEIO entre os nós i e j de um grafo é uma sequência alternante de nós
e arcos, começando em um dos nós i ou j e terminando no outro, tal que cada arco percorrido é incidente aos nós que o cercam na sequência. Um passeio é dito FECHADO quando começa e termina
no mesmo nó.
Um CAMINHO é um passeio que não contém nós repetidos. Dois nós estão CONECTADOS
se existe um caminho entre eles no grafo. Um grafo é dito CONEXO quando cada par de nós está
conectado, caso contrário ele é dito DESCONEXO.
Um passeio em um grafo é dito EULERIANO quando passa por todo arco exatamente uma vez.
À luz das definições acima, o Problema das pontes de Königsberg refere-se exatamente à existência
ou não de um passeio euleriano pela cidade (grafo), quando se considera as pontes como arcos e os
territórios (ilhas ou margens) como nós:
O argumento de Euler para as pontes de Königsberg: Consideremos um dos territórios
(ilhas ou margens), que chamaremos de território I. Suponhamos que o passeio não começa em I.
Então entramos em I pela primeira vez através de uma ponte que é incidente em I e saı́mos de I por
outra ponte incidente em I. Cada entrada-e-saı́da de I corresponde ao uso de duas pontes. Como I
tem um número ı́mpar de pontes incidentes, na última vez que usamos uma ponte incidente em I,
entramos em I e não podemos mais sair, ou seja, o passeio termina necessariamente em I. Assim, pelo
mesmo argumento, se o passeio começa em qualquer território, deve necessariamente terminar nos
outros três (contradição!), pois todos têm um número ı́mpar de pontes incidentes.
4
CAPÍTULO 1
O argumento anterior leva ao seguinte teorema:
Teorema 1.4. (Euler)
(a) Se um grafo conexo tem mais que dois nós com grau ı́mpar, então ele não admite um passeio
euleriano.
(b) Se um grafo conexo tem exatamente dois nós com grau ı́mpar, então ele admite passeio euleriano e todo passeio euleriano tem que começar em um desses nós de grau ı́mpar e terminar no
outro.
(c) Se um grafo conexo não tem nós com grau ı́mpar, então ele admite passeio euleriano e todo
passeio euleriano é fechado.
Exercı́cio: Prove a partir do teorema acima que um grafo conexo tem um passeio euleriano
fechado se, e somente se, todo nó tem grau par.
Exercı́cio: Quais dos grafos abaixo admitem um passeio euleriano? Em caso afirmativo, indique
um passeio euleriano.
Exercı́cio:
(a) Construa ou destrua UMA ponte em Königsberg para que se tenha um passeio euleriano
(indique o passeio).
(b) Mostre como se pode ter um passeio euleriano fechado construindo mais DUAS pontes em
Königsberg (indique o passeio).
(c) Mostre como se pode ter um passeio euleriano fechado construindo UMA ponte e destruindo
OUTRA em Königsberg.
(d) O que ocorre se destruirmos DUAS pontes em Königsberg?
Capı́tulo 2
Ciclos hamiltonianos
Problema: Seis cidades (nós) são ligadas por uma rede de estradas (arcos) conforme o mapa
(grafo) abaixo:
Um vendedor pretende, partindo de uma cidade, passar exatamente uma vez em cada uma das
demais cidades, terminando a viagem na cidade de origem.
É possı́vel realizar uma viagem nas condições acima?
Definição 2.1. Um CICLO é um passeio fechado no qual apenas o nó inicial-terminal se repete.
Um CICLO HAMILTONIANO é um ciclo que contém todos os nós de um grafo.
Observações:
(a) O problema acima equivale a perguntar se o grafo formado admite um ciclo hamiltoniano.
(b) É claro que para um grafo admitir um ciclo hamiltoniano é NECESSÁRIO que ele seja conexo.
(c) Não existem resultados gerais de caracterização dos grafos que admitem ciclos hamiltonianos.
(d) Problema do caixeiro viajante: achar um ciclo hamiltoniano de custo mı́nimo, sendo o custo
de um ciclo a soma dos custos dos arcos percorridos no ciclo.
5
6
CAPÍTULO 2
Proposição 2.2. Num ciclo com três ou mais nós são percorridos exatamente dois arcos incidentes
em cada nó do ciclo.
Corolário 1. Um grafo que tenha três ou mais nós e algum nó de grau menor ou igual a 1
não admite um ciclo hamiltoniano.
Exercı́cio: Resolva o problema inicial (do vendedor e as seis cidades): indique um ciclo hamiltoniano caso exista solução ou prove que não existe ciclo hamiltoniano algum.
Exercı́cio: Responda se os grafos abaixo admitem ou não um ciclo hamiltoniano. Indique um
ciclo hamiltoniano em caso afirmativo ou prove que não admite, no caso negativo.
Exercı́cio: Um grafo G = (N, A) é dito BIPARTIDO quando seu conjunto N de nós pode ser
particionado em DOIS subconjuntos tais que nós pertencentes a um mesmo subconjuntos não são
adjacentes.
(a) Prove que se um grafo bipartido G = (N, A) admite um ciclo hamiltoniano então os dois
subconjuntos da partição de N têm o mesmo número de elementos.
(b) Conclua que o grafo abaixo NÃO ADMITE um ciclo hamiltoniano.
(c) Construa um grafo bipartido com um número par de nós, todos com grau maior ou igual a
dois, e que não admite um ciclo hamiltoniano.
Capı́tulo 3
Árvores
Problema: Através de cabos telefônicos (arcos) entre pares de cidades (nós), deseja-se configurar
uma rede de comunicações (grafo) entre as sete cidades do mapa abaixo, de modo que possa haver
comunicação entre cada par de cidades, ou seja, cada par de cidades esteja conectado por pelo menos
um caminho na rede de comunicações (o grafo é conexo).
(a) É possı́vel obter uma rede (grafo) conexa com exatamente um caminho conectando cada par
de cidades? (neste caso é fácil ver que o grafo será MINIMALMENTE CONEXO, ou seja, a remoção
de qualquer arco irá tornar o grafo desconexo).
(b) Dentre todas as redes (grafos) conexas possivelmente obtidas na letra (a) acima, é possı́vel
obter uma de menor custo (ÓTIMA)?
Definição 3.1. Uma ÁRVORE é um grafo simples tal que para cada par de nós existe exatamente
um caminho que os conecta.
7
8
CAPÍTULO 3
Observações:
(a) O problema inicial equivale a perguntar se é possı́vel formar uma árvore com os nós (cidades)
dados e, em caso afirmativo, se existe uma árvore de menor custo.
(b) Um grafo G é uma árvore se, e somente se, G é conexo e a remoção de qualquer um de seus
arcos resulta em um grafo desconexo (uma árvore é um grafo MINIMALMENTE CONEXO).
(c) Uma árvore não admte ciclos com três ou mais nós (pois se admitisse haveria mais de um
caminho conectando dois nós) e a adição de um arco ligando dois nós que não eram ligados por um
arco gera um ciclo com três ou mais nós (uma árvore é um grafo MAXIMALMENTE LIVRE DE
CICLOS COM TRÊS OU MAIS NÓS).
(EXEMPLOS)
• PROCEDIMENTO DE CRESCIMENTO DE ÁRVORE (como obter árvores)
- Comece com um simples nó.
- Repita o que se segue um número (FINITO) qualquer de vezes: Se G é o grafo até então formado,
crie um novo nó e ligue-o por um arco novo a qualquer nó de G.
Teorema 3.2. Todo grafo obtido pelo procedimento de crescimento de árvore é uma árvore e toda
árvore pode ser obtida desta maneira.
Corolário 1. Toda árvore com n nós tem n − 1 arcos.
• O ALGORÍTMO GULOSO DE KRUSKAL (encontrando a árvore ótima)
- Considere n nós e nenhum arco.
- Construa um arco de menor custo entre dois nós distintos que não estejam ligados por um arco
e de maneira que não se obtenha um ciclo com três ou mais nós.
- Repita o procedimento acima até que se tenha n − 1 arcos.
Teorema 3.3. Dados n nós e nenhum arco, o Algorı́tmo Guloso produz uma árvore de menor custo
(árvore ótima) entre todas as possı́veis árvores com os n nós inicialmente dados.
Observação: Uma tentativa de adaptação do Algorı́tmo Guloso pode não funcionar para obter
um ciclo hamiltoniano ótimo (Problema do caixeiro viajante).
Exercı́cio: (a) USANDO O PROCEDIMENTO DE CRESCIMENTO DE ÁRVORE, resolva
a letra (a) do problema inicial, obtendo uma rede de comunicações minimalmente conexa entre as
cidades dadas. (b) Considerando os custos proporcionais às distâncias, USE O ALGORÍTMO GULOSO e obtenha uma rede de comunicações minimalmente conexa e de menor custo possı́vel (ótima)
entre as cidades dadas, resolvendo assim a letra (b) do problema inicial.
Árvores
9
Exercı́cio: Prove a Observação após o Teo 3.3
(Sugestão: considere os pontos A(0, 0), B(1, 0), C(0, 1) e D(9, 1))
Exercı́cio: Para cada um dos grafos dados abaixo, faça o que se pede.
- Responda se o grafo é uma árvore.
- Se o grafo não for uma árvore, justifique.
- Se o grafo for uma árvore, responda se é uma árvore de menor custo (custos proporcionais às
distâncias) considerando os nós dados. Se não for uma árvore de menor custo, exiba uma árvore de
menor custo com os nós dados.
10
CAPÍTULO 3
Capı́tulo 4
Emparelhamento em grafos
Problema: Temos um conjunto de seis tarefas (nós) a ser realizadas e seis funcionários (nós)
para realizar as tarefas. Quando um funcionário tem habilidade para realizar uma tarefa, ambos
serão ligados por um arco.
Cada funcionário Fi tem habilidade para realizar um conjunto {Tj } de tarefas, conforme o grafo
abaixo:
É possı́vel atribuir exatamente uma tarefa a cada funcionário de modo que todas as tarefas sejam
realizadas?
Definição 4.1. Uma grafo G = (N, A) é dito BIPARTIDO quando seu conjunto N de nós pode ser
particionado em dois subconjuntos tais que os nós pertencentes a um mesmo subconjunto não são
adjacentes.
Um EMPARELHAMENTO PERFEITO em um grafo bipartido é um conjunto de arcos A0 ⊂ A
tal que cada nó do grafo é incidente em exatamente um arco do conjunto A0 .
11
12
CAPÍTULO 4
Observações:
(a) O problema inicial equivale a perguntar se o grafo dadoi tem um emparelhamento perfeito.
(b) É claro que se um grafo bipartido G = (N, A) , sendo N = N1 ∪ N2 a partição de N , tem
um emparelhamento perfeito então #N1 = #N2 e N é obrigatoriamente par.
Teorema 4.2. (Teorema do emparelhamento) Um grafo bipartido G = (N, A) , sendo N = N1 ∪ N2
a partição de N , tem um emparelhamento perfeito se, e somente se, #N1 = #N2 e para qualquer
subconjunto N10 ⊂ N1 temos pelo menos #N10 nós em N2 adjacentes aos nós de N10 .
Observação: Vale a simetria no teorema acima.
Corolário 1. Se em um grafo bipartido todo nó tem mesmo grau d ≥ 1 , então o grafo contém um
emparelhamento perfeito.
Exercı́cio: Usando o Teorema 4.2, verifique se o problema inicial das seis tarefas para os seis
funcionários tem solução.
Exercı́cio: Prove o Corolário do Teorema 4.2.
Exercı́cio: Desenhe um grafo cujos nós são os subconjuntos de {a, b, c} e dois nós são adjacentes
se, e somente se, eles são subconjuntos que diferem por exatamente um elemento.
(a) Qual é o número de arestas e nós nesse grafo?
(b) Esse grafo é conexo? Ele tem um emparelhamento perfeito? (exiba um caso tenha) Ele admite
um ciclo hamiltoniano? (exiba um caso admita)
Exercı́cio: Verifique (justifique) se os grafos abaixo têm emparelhamentos perfeitos e exiba tais
emparelhamentos nos casos afirmativos.
Exercı́cio: Numa festa há 286 convidados. Cada homem conhece 30 mulheres e cada mulher
conhece 30 homens (o conhecimento é mútuo). A organização da festa deseja saber qual o número
máximo de casais que podem estar dançando simultaneamente para providenciar o espaço adequado.
Que número é esse? (prove).
Capı́tulo 5
Grafos planares:
Colorindo grafos e mapas
Definição 5.1. Uma grafo simples e conexo é chamado PLANAR quando ele pode ser desenhado
como um mapa no plano: seus nós correspondem a pontos distintos no plano e seus arcos são
curvas plana (ligando os nós) as quais não se intersectam em pontos que não sejam os nós.
EXEMPLO: K4 = grafo completo sobre 4 nós = grafo com 4 nós onde cada nó está ligado a
todos os demais.
Observação: Um grafo planar, quando representado de forma planar, divide o plano em uma
quantidade finita de regiões, sendo uma delas ilimitada e as demais (se existirem) limitadas.
EXEMPLO:
13
14
CAPÍTULO 5
Teorema 5.2. (Fórmula de Euler) Seja G um grafo planar. Se v é o número de nós de G, a é o
número de arcos de G e f é o número de regiões do plano determinadas pela sua forma planar, então
v−a+f =2
Corolário 1. Um grafo planar sobre n ≥ 3 nós tem no máximo 3n − 6 arcos. (Exercı́cio)
Exercı́cio: Existem 3 casas e 3 fontes. Podemos construir um caminho de toda casa para toda
fonte de modo que esses caminhos não se cruzem? (os caminhos não são necessariamente linhas retas)
Exercı́cio: Prove que K5 (grafo completo sobre 5 nós) não é um grafo planar.
Exercı́cio: O grao obtido pela omissão de um arco de K5 é planar?
Exercı́cio: O Grafo de Petersen é planar?
•
Colorindo grafos
Regra para coloração de grafos: nós adjacentes têm que ser coloridos com cores diferentes.
Se podemos colorir um grafo com k cores (dentro da regra acima), dizemos que o grafo é
k−COLORÍVEL.
O menor valor de k para o qual o grafo é k−colorı́vel é chamado de NÚMERO CROMÁTICO do
grafo.
Observações:
(a) É óbvio que se um grafo tem n nós então n cores são sempre suficientes para colori-lo (o grafo
é n−colorı́vel) e seu número cromático é menor ou igual a n.
(b) Um grafo é 2−colorı́vel se, e somente se, ele é bipartido.
Teorema 5.3. (Teorema de Brooks) Se todo nó em um grafo tem grau no máximo d, então o grafo
pode ser colorido com d + 1 cores.
Exercı́cio: Obtenha o número cromático dos grafos a seguir:
Grafos planares:
Colorindo grafos e mapas
•
15
Colorindo mapas
Consideremos agora o problema de colorir um mapa que seja uma representação plana de diversas
regiões (paı́ses, estados, etc.) CONEXAS (dois pontos de uma mesma região podem ser “ligados por
umam estrada dentro da própria região”).
É natural pedirmos que regiões vizinhas (com fronteira de comprimento não-nulo comum) tenham
cores diferentes.
IDÉIA: Cada região conexa será representada por um nó e regiões (nós) vizinhas serão ligadas
por um arco, formando assim um GRAFO DUAL do mapa original. O grafo dual assim obtido será
um grafo planar (desafio: tente provar) e o nosso problema de colorir o mapa original se reduz ao
problema de colorir seu grafo dual.
Exercı́cio: Obtenha os grafos duais (em suas representações planares) para os mapas dados
abaixo:
Exercı́cio: Obtenha os números cromáticos dos grafos duais obtidos no exercı́cio anterior e colora
os grafos e os mapas segundo os números obtidos.
Exercı́cio: Dê exemplo de um mapa para mostrar que se admitirmos regiões desconexas, o grafo
dual obtido não é necessariamente planar.
16
CAPÍTULO 5
Teorema 5.4. (Teorema das 4 cores) Todo grafo planar pode ser colorido com 4 cores.
Corolário 1. Todo mapa que é representação planar de regiões conexas pode ser colorido com 4
cores.
Exercı́cio: Exiba um mapa que precise de mais do que 4 cores para ser colorido.
Exercı́cio: Um grafo G0 é dito um SUBGRAFO de um grafo G quando G0 é obtido a partir de
G eliminando-se nós (e seus arcos incidentes) ou arcos de G.
(a) Prove que se todo subgrafo de um grafo G tem um nó de grau menor ou igual a d então G é
d + 1 colorı́vel. (Sugestão: indução sobre o número de nós de G)
(b) Prove que todo grafo planar tem um nó de grau menor ou igual a 5. (Sugestão: use o Corolário
do Teorema 5.2)
(c) Conclua que todo grafo planar pode ser colorido com 6 cores (“Teorema das 6 cores”)
Referências
[1] Lovász, L. e outros, Matemática Discreta, Coleção Textos Universitários, SBM, Rio de
Janeiro, 2003.
[2] Santos, J. P. O. e outros, Introdução à Análise Combinatória, Editora Unicamp, Campinas,
2002.
17