EEL 215 - Circuitos Elétricos II Relação de Transformação TRANSFORMADORES MEDIÇÃO DA RELAÇÃO DE TRANSFORMAÇÃO "Não se pode ensinar alguma coisa a alguém, pode-se apenas auxiliar a descobrir por si mesmo.” Galileu Galilei RESUMO O objetivo deste texto é apresentar uma metodologia para a medição da relação de transformação de transformadores trifásicos (considerando-se todas as conexões padronizadas) a partir do conhecimento prévio de seu defasamento angular. Adicionalmente é mostrada a influência grandeza na leitura do equipamento e efetuase urna análise de erros em relação aos valores obtidos pelo método da medição direta da relação de transformação com níveis de tensões reduzidos (método do voltímetro) Em função do exposto e visando a diminuir a taxa de incerteza na utilização dos dados de ensaio, efetua-se uma análise crítica dos erros inerentes aos métodos e fornece-se procedimentos adequados para minimizá-los. 2.0 - PRINCÍPIO DE FUNCIONAMENTO DO TRANSFORMADOR MONOFASICO O transformador monofásico, em sua forma mais elementar, constitui-se de um núcleo de material magnético e enrolamentos, como mostra esquematicamente a Figura 1. 1.0 - INTRODUÇÃO A medição da relação de transformação de um transformador é padronizada como ensaio de rotina e como teste básico em programas de manutenção preventiva em transformadores reparados ou submetidos à reformas ou, ainda, no comissionamento das unidades. A sua importância se prende ao fato de que um acompanhamento efetivo poderá indicar a presença de problemas, bem como, a adaptabilidade do transformador ao sistema que se insere (por exemplo, na operação em paralelo). Os métodos mais freqüentemente empregados para a sua obtenção são o do voltímetro e o da medição da relação de espiras através de um equipamento construído especificamente para este fim. É claro que qualquer um deles deve oferecer valores suficientemente precisos para que sejam válidos para os propósitos citados; inclusive, a tolerância normalizada nos ensaios de rotina é o menor valor entre 10% da tensão de curtocircuito em percentagem ou ± 0,5% do valor da tensão nominal dos diversos enrolamentos se aplicada tensão nominal no primário. Em ambas as metodologias verifica-se que existem erros e incertezas em seus empregos e resultados, Neste aspecto, o método do voltímetro é restritivo em muitos casos, principalmente quando são aplicadas tensões reduzidas em relação à nominal; por sua vez, a aplicação do medidor de relação de espiras a transformadores trifásicos apresenta várias nuances que podem levar a enganos brutais. Figura - 1 – Transformador monofásico elementar O funcionamento do transformador monofásico baseia-se no principio de. que a energia elétrica pode ser transferida entre dois circuitos devido ao fenômeno da indução magnética. Aplicando-se a tensão U1, no primário do transformador, circulará uma pequena corrente denominada “corrente em vazio”, representada neste texto por I0 . Se a tensão aplicada é variável no tempo, a corrente I0 também o é. De acordo com a lei de Ampère, tem-se: H.l = N1I0 (1) onde: H é a intensidade do campo; l é o comprimento do circuito magnético; N1I0 é a força magnetomotriz. ________________________________________________________________________________ Medição da Relação de Transformação - 1 EEL 215 - Circuitos Elétricos II Relação de Transformação A expressão (1) pode ser rescrita como: Reφ = N110 (2) onde: Por outro lado, as bobinas, geralmente, são montadas concêntricamente, para aproveitamento de uma parcela do fluxo de dispersão; como dado prático, normalmente realiza-se esta montagem com as bobinas de maior tensão envolvendo as de menor. Tal disposição não altera o funcionamento do transformador, apenas otimiza o aproveitamento do fluxo. Re - relutância do núcleo; φ- fluxo magnético. Desta forma, verifica-se que a força magnetomotriz impulsiona o fluxo magnético pelo núcleo, sendo limitado pela relutância.. Naturalmente, se a corrente é variável no tempo, o fluxo magnético também o é. Por outro lado, sabe-se pela lei de Faraday, que “sempre que houver movimento relativo entre o fluxo magnético e um circuito por ele cortado., serão induzidas tensões neste circuito”. Figura 2 – Núcleo do transformador – Representação esquemática 3.0 - O TRANSFORMADOR EM OPERACÂO Pelo exposto, no transformador da Figura 1, existirão tensões induzidas no primário (E1) e no secundário (E2) , devido à variação do fluxo em relação às espiras. Considere-se a figura 3. Os valores eficazes das tensões induzidas são dados por: E1 = 4,44.N1.f.S.Bmax E2 = 4,44N2.f.S.Bmax (3) (4) onde: E1, E2 - valores eficazes das tensões induzidas no primário e secundário, em[V]; N1, N2 - número de espiras dos enrolamentos primário e secundário f-- freqüência, [Hz]; S- seção transversal do núcleo do transformador, [m2 ]; B- valor da indução magnética no núcleo, [wb/m 2]. Observe-se que: φm =B.S (5) sendo φm o fluxo magnético (mútuo) do núcleo do transformador, [wb]. Deve-se observar que o transformador não é ideal e, sendo assim, os enrolamentos possuem resistência e capacitância (além, naturalmente, da indutância) e existem fluxos de dispersão. Os efeitos capacitivos tornam-se importantes em transformadores acoplados à circuitos eletrônicos com freqüências extremamente elevadas (em geral até 400 Hz, tais efeitos são desprezíveis) ou tensões com altos valores. Figura 3 – Transformador monofásico em operação Com o transformador operando em vazio, ou sem carga, a corrente I0 magnetiza o transformador e induz as tensões E1 e E2. Fechando-se a chave S do circuito secundário do transformador, haverá circulação da corrente I2 em seu enrolamento, cujo valor depende exclusivamente da carga. Como visto, de acordo com a lei de Ampère, I2 criará o fluxo de reação φ2 e de dispersão φdisp2 , sendo que o primeiro tende a anular φm. Para que o transformador continue magnetizado, haverá uma compensação de fluxo no primário, ou seja: para manter a magnetização, o transformador exigirá da rede uma corrente suplementar a I0, de modo a compensar φ2 ; esta corrente receberá a denominação de I’2, a qual cria o fluxo φ1. Assim, a corrente primária I1 é: I1= I 02 + I 22 (6) de onde: I0= I 12 − I 22 (7) ________________________________________________________________________________ Medição da Relação de Transformação - 2 EEL 215 - Circuitos Elétricos II Relação de Transformação 4.0 – BANCO COM TRÊS TRANSFORMADORES Para executar a ligação dos três transformadores monofásicos independentes é necessário conectar os primários e os secundários entre si. Nesta situação, há a possibilidade de conectá-los ou em delta (triângulo) ou em estrela. Este sistema apresenta custo maiores em relação a uma unidade trifásica. Entretanto, possibilita a existência de apenas um transformador monofásico de reserva com 1/3 da potência total para os três, enquanto o trifásico exige outro de igual potência. A ligação de bancos monofásicos é freqüentemente empregada em instalações de grande potência, onde o custo da unidade reserva resulta significativo. Além disto, em caso de falha de uma unidade, o banco ainda pode operar em uma conexão especial, porém com capacidade reduzida, mas sem interrupção de fornecimento. 5.0 - TRANSFORMADOR TRIFASICO Partindo do princípio que o transformador trifásico agrupa três monofásicos em um, a composição entre os núcleos mais evidente é a mostrada na figura 1. Figura 4 – Ligações delta e estrela Desta forma, combinando-se estes tipos de ligações, a transferência de energia realiza-se através das seguintes conexões: D Primário Secundário d D y Y d Y y Sendo “D” e “Y”, respectivamente, as ligações delta e estrela do lado primário e “d” e “y” as equivalentes no secundário. A figura 5 mostra algumas maneiras de conectálas a título de exemplo. Figura 6 - Núcleos monofásicos compondo o trifásico. Um sistema trifásico simétrico e equilibrado possui três correntes com mesmo módulo, porém defasadas de 120º elétricos uma das outras. Pela lei de Ampère, elas originam fluxos nos núcleos monofásicos, também defasados de 120º. Analogamente às correntes trifásicas, quando os fluxos juntarem-se em um ponto, sua soma será nula, o que ocorre no local de união dos três núcleos. Sendo assim, não há necessidade de sua utilização é, portanto, é conveniente retirá-lo do circuito como medida de economia de material. H1 e H2 são os terminais iniciais e finais do primário X1 e X2 são os terminais iniciais e finais do secundário Figura 5 – Conexões em banco com três transformadores monofásicos Figura 7 - Núcleo trifásico ideal. ________________________________________________________________________________ Medição da Relação de Transformação - 3 EEL 215 - Circuitos Elétricos II Relação de Transformação O núcleo trifásico da figura 7 é o ideal; entretanto, tem uma forma inconveniente e há uma utilização excessiva de material em sua construção, o que se reflete nos custos e inviabiliza a sua utilização. A solução que se adota, em termos práticos, é bastante simples, ou seja: retira-se um dos núcleos, inserindo entre as colunas (ou pernas) laterais, uma outra com as mesmas dimensões. Portanto: KN = E1 N 1 = E2 N 2 (9) Por outro lado, prova-se que: KN = E1 N 1 I 2 = ≅ E2 N 2 I1 (10) No funcionamento em vazio, tem-se que: I1 = I 0 (11) onde: I0 - corrente em vazio. Devido a este fato, como citado anteriormente, a queda de tensão primária é mínima; assim: U 1 = E1 Figura 8 - Núcleo trifásico real. O circuito magnético das três fases, neste caso, resulta desequilibrado. A relutância da coluna central é menor que as outras, o que origina uma pequena diferença nas correntes de magnetização de cada fase. (12) Além disto, nesta condição: U 2 = E2 (13) Assim: 6.0 – RELAÇÃO DE TRANSFORMAÇÃO TRANSFORMADORES MONOFÁSICOS – KN = Seja o transformador monofásico representado pela figura 1. E1 U 1 = E2 U 2 (14) A expressão (14) é importante, pois E1 e E2, são inacessíveis a uma medição; assim, utilizando-se um voltímetro no primário obtêm-se U1, e, no secundário, estando o transformador em vazio, U2. Desta forma, achase a relação do número de espiras com pequeno erro. b) Relação de Transformação Real Figura 9 - Transformador monofásico em carga A relação de transformação das tensões de um transformador monofásico é definida de duas formas: a) Relação de Transformação Teórica ou Relação de Espiras Definida por: ¶ KN = E1 4.44 N 1 fBS = E 2 4.44 N 2 fBS (8) Ao aplicar a carga ZC ao secundário, a corrente 12 circula pelo secundário e I1 assume valores superiores a I0. Assim, haverá queda de tensão no primário e no secundário e, portanto: U 2 ≠ E2 (15) Nestas condições, define-se a relação de transformação real, ou a relação entre as tensões primárias e secundárias quando do transformador em carga, ou seja: U1 I 2 ≅ (16) U 2 I1 ________________________________________________________________________________ K= Medição da Relação de Transformação - 4 EEL 215 - Circuitos Elétricos II Relação de Transformação Eventualmente, se a queda de tensão secundária for pequena (o que acontece para transformadores bem projetados) pode-se supor que: KN = K (20) então: KN ≅ K (21) b) Na figura 10b: U E N I K= 1 = 1 = 1 ≅ 2 U 2 E2 N 2 I1 (18) K= Observe-se que: a) se K>1, o transformador é abaixador; e, b) se K<1, o transformador é elevador. – U 2 = E2 e (17) ou seja: 7.0 U 1 ≅ E1 RELACÃO DE TRANSFORMACÃO TRANSFORMADORES TRIFÂSICOS Nos transformadores trifásicos a relação de transformação real também é definida como em (18). Entretanto, devido à conexão dos enrolamentos (El e E2 são tensões induzidas entre os terminais dos enrolamentos), ela não será, em todos os casos, igual à relação de espiras. A figura 10 mostra duas conexões de transformadores trifásicos. U1 U2 (22) Como os enrolamentos podem estar conectados de diversas maneiras, nota-se que para cada modo de ligação haverá uma diferença entre a relação de transformação e de espiras; a tabela 1 mostra os valores de K em função de KN para cada ligação. Ligação Dd Dy Dz Yy K KN KN 3 2K N 3 KN Yd 3K N Yz 2K N 3 Tabela 1 - Valores de K em função de KN, para as diversas conexões Figura 10 - Conexões dos transformadores trifásicos Sendo assim, as relações de transformação K e KN para cada caso seriam: a) Na figura 10a: K= U1 U2 e KN = E1 N1 = E2 N 2 (19) e, estando o transformador em vazio, tem-se: ________________________________________________________________________________ Medição da Relação de Transformação - 5 EEL 215 - Circuitos Elétricos II Relação de Transformação MEDIÇÃO DA RELAÇÃO DE TRANSFORMAÇÃO 1.0 - DETERMINAÇÃO DA RELAÇÃO DE TENSOES O ensaio de relação de tensões realiza-se aplicando a um dos enrolamentos uma tensão igual ou menor que a sua tensão nominal, bem como, freqüência igual ou maior que a nominal. Para transformadores trifásicos, apresentando fases independentes e com terminais acessíveis, opera-se indiferentemente, usando-se corrente monofásica ou trifásica, ou seja, como for mais conveniente. Se os enrolamentos da tensão superior estiverem ligados em estrela com o neutro inacessível, usa-se corrente trifásica, operando-se do mesmo modo que com os transformadores monofásicos. Os métodos usados para o ensaio de relação de tensões são: a) b) c) d) Método do voltímetro; Método do transformador padrão; Método do resistor potenciométrico; Método do transformador de referência de relação variável. A NBR 5356/81 estabelece que este ensaio deve ser realizado em todas as derivações, o que se constitui em uma boa prática, principalmente, na recepção do transformador. Observe-se que as tensões deverão ser sempre dadas para o transformador em vazio A citada norma admite uma tolerância igual ao menor valor entre 10% da tensão de curto circuito em porcentagem ou ± 0,5% do valor da tensão nominal dos diversos enrolamentos, se aplicada tensão nominal no primário. Analisa-se a seguir, os métodos do voltímetro e do transformador de referência de relação variável, por serem os mais utilizados. 2.0 - MÉTODO DO VOLTÏMETRO O principio deste método é alimentar o transformador com uma certa tensão e medi-la juntamente com a induzida no secundário. A leitura deve ser feita de forma simultânea com dois voltímetros (e TP’s, se necessário). Ainda recomenda-se que se faça um novo grupo de leituras permutando-se os instrumentos visando compensar seus eventuais erros. A média das relações obtidas desta forma é considerada como a do transformador. Observe-se que em geral, por facilidade e segurança, a alimentação do transformador é feita pelo lado de TS (Tensão Superior) com níveis reduzidos de tensão em relação nominal do tap considerado; isto acarreta dois problemas fundamentais, a saber: a) A fonte, na maioria dos casos, apresenta tensões desequilibradas, mascarando os resultados das medições; b) Se aplicados, por exemplo, três níveis distintos de tensões, mesmo balanceadas, podem resultar três valores diferentes de relação de transformação. Em ambas as situações, os erros e incertezas descaracterizam os objetivos de se medir a relação de transformação. Em primeiro caso é possível determinar-se uma relação de transformação média, a qual representa mais adequadamente a do transformador. Sugere-se que o seu cálculo sela feito empregando-se: U H + U H0 m K= U X +U X0 n (23) Onde: a) U H = U H 1H 2 + U H 1H 3 + U H 2 H 3 (24) b) U X = U X 1X 2 + U X 1X 3 + U X 2 X 3 (25) c) Se a ligação do lado considerado for delta ou estrela com neutro inacessível: U H0 = 0 (26) e/ou UX0 = 0 (27) m=3 (28) e/ou n=3 (29) ________________________________________________________________________________ Medição da Relação de Transformação - 6 EEL 215 - Circuitos Elétricos II Relação de Transformação m=6 d) Se a ligação for estrela com neutro acessível, tem-se: U H 0 = (U H 1H 0 + U H 2H 0 + U H 3 H 0 ) 3 (30) n=6 (26) A Tabela 2 exemplifica o exposto para um transformador trifásico de 30 kVA, 13800-13200-126001200/220 V, Dy 1, ensaiado conforme prescrito no método em análise. e/ou U X 0 = (U X 1 X 0 + U X 1 X 0 + U X 3 X 0 ) 3 Buchas Tap (V) 13800 13200 12600 12000 (25) e/ou (31) H1H2 H1H3 H2H3 X1X2 X1X3 X2X3 X1X0 X2X0 X3X0 K 523 530 583 520 527 533 535 524 524 531 534 521 8.33 8.79 9.26 9.54 8.35 8.81 9.28 9.55 8.28 8.76 9.22 9.48 4.84 5.12 5.38 5.55 4.79 5.90 5.35 5.50 4.81 5.10 5.36 5.52 62.9567 58.732 57.596 54.653 Tabela 2 Valores medidos entre buchas e a relação de transformação média - Evidentemente, o acompanhamento da relação de transformação entre buchas de mesmo índice fica prejudicado, limitando a aplicabilidade do procedimento. Por outro lado, o emprego de tensões reduzidas acarretam na diminuição da corrente em vazio. Isto resulta em quedas de tensões distintas para cada tensão aplicada, ou seja, mede-se a tensão primária e secundária, porém esta última será proporcional á tensão primária subtraída da queda de tensão causada. Pelo, exposto, sugere-se, para minimizar as incertezas, que sejam aplicadas várias tensões reduzidas, efetuadas as medições correspondentes, calculadas as relações, a sua medida (K) e respectivo desvio padrão, (σK). Neste caso, verifica-se a consistência dada por: σK K ≤ 0.1 (32) Se houver consistência, o valor médio será considerado como a relação de transformação para o tap considerado. Em caso contrário, deve-se executar novo elenco de medidas e repetido o processo. Para o transformador do exemplo anterior, aplicando-se o método como exposto e as expressões anteriores, obteve-se os valores constantes na tabela 3 para o tap de 12000V. UH/3 (UX+UX0)/6 K 570 8.64 54.42 494 9.07 54.47 500 9.16 54.60 520 9.51 54.65 547 10.00 54.70 K = 54,568 (33) e o desvio padrão: σK = 0.1190 (34) e: σK K = 0.0022 (34) O resultado de (30) indica a consistência dos dados e, assim, a média será considerada a relação de transformação do tap. Como a relação de placa é de 54,5455, o erro é de apenas 0.04%. 3.0 - ROTEIRO PRÁTICO 1) Pelo método do voltímetro, verificar a relação de transformação de um trafo monofásico, realizando a medição com várias tensões de entrada e comparar com os dados de placa do transformador. 2) Conectar um banco de transformadores em DY e medir a relação usando (23). Comparar com o exposto na Tabela 1. 2.1) Usando um ociloscópio, medir a defasagem angular da tensão de entrada e saída do banco DY. Tabela 3 - Relações de transformação obtidas com tensões reduzidas. A média das relações é: ________________________________________________________________________________ Medição da Relação de Transformação - 7
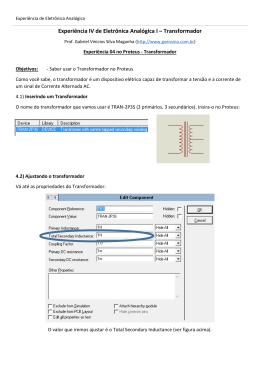
Download