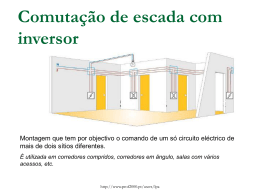
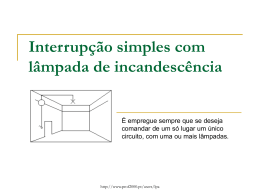
Física Geral
2010/2011
10 – Campo Eléctrico:
A força electromagnética entre partículas carregadas é uma das forças fundamentais
da natureza. Uma das suas manifestações é a força eléctrica.
Existem dois tipos de cargas eléctricas, positivas e negativas. Cargas do mesmo sinal
repelem-se e cargas de sinal oposto atraem-se.
Num sistema isolado a carga conserva-se.
A carga q existe em quantidades discretas ou seja, em múltiplos (N) de um valor e,
sendo -e o valor da carga do electrão e +e o valor da carga do protão:
q  Ne
Electrões livres: Electrões que ocupam a camada preenchida mais exterior em cada
átomo, portanto com uma ligação mais fraca ao seu núcleo. No caso dos metais estes
electrões livres movem-se pela estrutura microscópica não estando ligados a nenhum
átomo específico.
Em termos do transporte de electrões livres através de um material, podemos
classificá-los em condutores, isolantes e semicondutores.
Condutores: materiais onde existem electrões livres.
Isolantes: materiais em que todos os electrões estão ligados ao núcleo dos átomos e
portanto não se podem mover através do material.
Semicondutores: classe de materiais que possuem propriedades entre os condutores
e os isolantes.
Lei de Coulomb:
Fe  ke
q1 q2
r2
Escola Superior Náutica Infante D. Henrique
Departamento de Engenharia Marítima
1
Física Geral
2010/2011
Em que:
ke  8.9875  109 N m2C 2
(Constante de Coulomb)
ke 
 0  8.8542  1012 C 2 N 1m2
1
4 0
(Permitividade no vazio)
Carga do electrão: -e, carga do protão: +e, em que:
e  1.60219  1019 C
Na Lei de Coulomb, o vector que representa a força que uma carga pontual q1 exerce
sobre outra carga pontual q2 á distância r uma da outra é:

q q
F12  ke 1 2 2 rˆ
r
A figura seguinte representa os vectores força para duas cargas pontuais com o
mesmo sinal (positivas):
Ou, para cargas de sinal oposto:
Se uma carga está sob a influência de várias outras cargas, a força resultante que
actua nessa carga, corresponde á soma de cada força exercida por cada uma das
cargas.
Escola Superior Náutica Infante D. Henrique
Departamento de Engenharia Marítima
2
Física Geral
2010/2011
Campo Eléctrico
Na região em torno de um objecto carregado electricamente, existe um campo
eléctrico. Quando outro objecto carregado com carga q0 é colocado nessa região,
actua sobre ele uma força eléctrica.
Sendo Fe a força exercida sobre q0 ,o vector campo eléctrico no ponto do espaço onde
é colocada a carga é:

 Fe
E
q0


Fe  q0 E

Á carga q0 chama-se, carga de teste e pode funcionar como “detector” do campo
eléctrico.
O campo eléctrico apenas depende da carga ou da distribuição de cargas que lhe dá
origem, tal como o planeta Terra dá origem ao campo gravítico á sua volta, e é
independente da carga de teste, tal como o campo gravítico da Terra é independente
das massas dos objectos sob a sua influência e das suas massas e distribuição no
espaço.
Notar a semelhança entre a expressão que nos dá o valor da força eléctrica:


Fe  q0 E
e a expressão para a força gravítica:


Fg  m g
O vector que representa a força eléctrica exercida por uma carga q sobre uma carga
de teste q0 á distância r, é dada por:

qq
Fe  ke 2 0 rˆ
r
Então, o vector campo eléctrico que representa o campo eléctrico criado pela carga q
é dado por:

q
E  ke 2 rˆ
r
Escola Superior Náutica Infante D. Henrique
Departamento de Engenharia Marítima
3
Física Geral
2010/2011
Se estivermos na presença de um conjunto de cargas pontuais, aplica-se o princípio
da sobreposição, ou seja, num dado ponto P do espaço, o campo eléctrico total devido
a um conjunto de cargas pontuais é a soma dos campos eléctricos devido a cada uma
das cargas individualmente:

q
E  ke  2i rˆi
i ri
Onde ri é a distância da carga i ao ponto P, qi é o valor da carga i e r̂i é p vector
unitário que aponta da carga i para o ponto P.
Linhas de campo eléctrico
As linhas de campo eléctrico são uma representação espacial do campo eléctrico.
Estas linhas são tangentes ao vector campo eléctrico em cada ponto e o número de
linhas por unidade de área que passam numa região é proporcional á magnitude do
campo eléctrico nessa região.
Por exemplo para uma carga pontual positiva, as linhas dispõem-se radialmente e
apontam para fora, conforme ilustra a figura:
Ou, inversamente se estamos na presença de uma carga negativa:
As linhas de campo não se podem cruzar.
Escola Superior Náutica Infante D. Henrique
Departamento de Engenharia Marítima
4
Física Geral
2010/2011
Quando, por exemplo duas cargas interagem uma com a outra, as linhas de campo
começam na carga positiva e acabam na carga negativa, ou terminam no próprio
espaço, conforme a seguinte figura:
No entanto, podem existir linhas que não unem as duas cargas e estas podem estar
dispostas de uma forma assimétrica, caso as cargas não sejam iguais ou simétricas,
conforme ilustra a figura seguinte:
Sendo o numero de linhas que entram ou saem, proporcional aos valores das
respectivas cargas, podemos estabelecer a seguinte relação:
N1 q1

N 2 q2
Onde N1 e N 2 são o numero de linhas que saem ou entram de q1 e q2 ,
respectivamente.
Movimento de partículas carregadas num campo eléctrico uniforme
Quando uma partícula de massa m carga q está sujeita a um campo eléctrico
uniforme, a força exercida sobre ela é:



Fe  qE  ma
Então:

 qE
a
m
Escola Superior Náutica Infante D. Henrique
Departamento de Engenharia Marítima
5
Física Geral
2010/2011
Portanto, se queremos saber informações sobre o movimento da partícula, a uma ou
mais dimensões, podemos usar as equações do movimento já estudadas, por
exemplo:
1
x  x0  v0t  at 2
2
Fluxo do campo eléctrico
Considerando uma superfície de área A, perpendicular a um campo eléctrico E, o
fluxo eléctrico através desta área é:
 E  EA
Que é proporcional ao numero de linhas do campo eléctrico que atravessa essa
superfície.
Considerando uma superfície atravessada pelas mesmas linhas de campo mas que
faz um ângulo  com a primeira:
Fluxo eléctrico:
 E  EA'

 E  EA cos 
Escola Superior Náutica Infante D. Henrique
Departamento de Engenharia Marítima
6
Física Geral
2010/2011
Considerando um elemento de área Ai numa superfície fechada, o fluxo eléctrico
através desse elemento é:
 E  Ei Ai cos i


 Ei  Ai
Assim, para toda a superfície, o fluxo total é a soma do fluxo nos elementos de área
infinitesimais que compõem a superfície:
 E  lim
A0


i
i
 E  A
i


 E  dA

Superficie
Ou:
 
 E   E  dA
Lei de Gauss
Se considerarmos uma superfície esférica com uma carga pontual no seu centro, o
campo eléctrico é uniforme em toda a superfície, pela simetria do problema, e o vector
campo eléctrico é sempre perpendicular a essa superfície, então o fluxo eléctrico é:


 E   Ei  dA   E.dA  E  dA
Já vimos que:
E  ke
q
r2
Como temos uma superfície esférica:
Então:
 E  ke
 dA  4 r
2
q
q
4 r 2  4 ke q 
2
r
0
Escola Superior Náutica Infante D. Henrique
Departamento de Engenharia Marítima
7
Física Geral
Este resultado:
2010/2011
E 
q
0
Pode ser generalizado para enunciarmos a Lei de Gauss, ou seja o fluxo através de
qualquer superfície fechada que tenha uma carga q no seu interior, é dado por:
  q
 E   E  dA 
0
Deve considerar-se que apesar de q ser o valor da carga no interior da superfície
fechada, o valor do campo eléctrico E corresponde ao campo eléctrico total, que pode
assim ter contribuições tanto do interior como do exterior da superfície.
Escola Superior Náutica Infante D. Henrique
Departamento de Engenharia Marítima
8