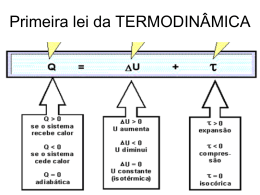
Física
Frente III
CAPÍTULO 5 - TERMODINÂMICA
AULAS 12 A 16
Introdução
A Termodinâmica é o ramo da física
que estuda as relações entre calor, temperatura, trabalho e energia.
Todo estudo na termodinâmica toma como referência um Sistema Termodinâmico, que é um conjunto
constituído de um fluido (na maioria dos casos, um gás
perfeito) contido em um recipiente, podendo estar ou
não em contato direto com o ambiente. Os sistemas
Fornecendo calor Q ao sistema, por meio de uma
podem ser classificados da seguinte maneira:
fonte térmica, o gás expande-se, deslocando o êmbolo
de uma distância x. Na situação final, o volume do gás é
Sistema Aberto: Através da fronteira, pode-se trocar V e a temperatura é T , mantendo-se a pressão cons2
2
com o meio externo energia e matéria.
tante P2 = P1. O gás exerceu uma força F sobre o êmSistema Fechado: Pode-se trocar energia, mas não
bolo, deslocando-o de x e realizando um trabalho 
matéria.
Sistema Isolado: A fronteira do sistema impede trocas dado por:
  F.x
Mas, F  P.A sendo P a pressão do gás e A, a
Estudaremos nesse curso os conceitos envolvi- área do êmbolo. Então:
dos na Termodinâmica dos Gases Perfeitos. Sob esse
O produto Ax = ∆V = V2 – V1 é a variação de volume
aspecto, podemos afirmar que os Gases Perfeitos:
ocorrida. Assim, o trabalho realizado pelo gás sobre o

Recebem (ou cedem) energia do meio sob a meio exterior, numa expansão isobárica, é dado por:
forma de Calor (Q).
Convenção:
Q > 0 se o gás recebe calor
Q < 0 se o gás cede calor
2
1
de energia e matéria.
  P.A.x
  P.V  P.(V  V )
Obs: Numa compressão, a variação de volume é nega
Armazenam (ou perdem) parte dessa energia, tiva, e o trabalho realizado é negativo. Assim, quando
variando sua Energia Interna (U), aquecendo-se ou um gás é comprimido, está recebendo energia do meio
resfriando-se.
exterior.
A Energia Interna de um Gás Perfeito monoatômico
pode ser obtida por:
3
3
U  nRT  PV
2
2
A variação da energia interna é dada por:
3
U  nR T
2
Assim, numa transformação termodinâmica temos que:
V2  V1  V  0    0
V1  V2  V  0    0
  P.V  P.(V  V ) 
2
1

Se o volume é constante temos
= 0.
Ao plotarmos em um diagrama PxV os dados da
curva da transformação P(V) temos que o trabalho é
numericamente igual à área embaixo da curva.
P
U  0  T  0  Aquecimento
U  0  T  0  Re sfriamento
U  0  T  0  T  cons tante

Transferem a energia restante ao meio, sob a
forma Trabalho.
Cálculo do Trabalho () em uma Expansão Gasosa
Isobárica
Considere um gás contido num cilindro cujo êmbolo
pode se movimentar livremente e sobre o qual há um
peso de massa m. Durante qualquer transformação
sofrida pelo gás, a pressão mantém-se constante, pois o
peso colocado sobre o êmbolo não varia. Sejam P1 a
pressão, V1 o volume e T1 a temperatura do gás na situação inicial.
P1
P2

V1
V2
V
__________________________________________________________________________________________________________________
CASD Vestibulares
Física - Termodinâmica
239
1ª Lei da Termodinâmica
A 1ª Lei da Termodinâmica é, nada mais nada menos, do que a Lei da Conservação da Energia. Assim,
em uma transformação termodinâmica, o balanço energético entre as quantidades de energia interna (U) e
externa (calor e trabalho) deve satisfazer essa lei. Analiticamente, temos:
U  Q  
Essa expressão é válida para qualquer sistema
termodinâmico.
Aplicações
Transformação Isocórica: V = cte (Isovolumétrica)
ção
Como nesse tipo de transformação não há variade volume, então o trabalho é zero:
. Assim:
Transformação Cíclica
Transformação Cíclica (ou apenas ciclo) de
certa massa gasosa é um conjunto de transformações
em que, após seu término, a massa gasosa encontra-se
exatamente no mesmo estado em que se encontrava
inicialmente.
Assim em toda transformação cíclica temos:
U  0 , pois T  T
V  0    0
F
U  Q
Q 
V
O calor é chamado
QV , pois é trocado a volume cons-
tante.
Transformação Isobárica: P = cte
0
Logo, para qualquer ciclo temos:
Um diagrama PxV comum para este tipo de transformação é dado na figura abaixo:
Neste tipo de transformação gasosa, a 1ª Lei da
Termodinâmica deve ser aplicada com todos os seus
termos, pois nenhum deles se anula. Então:
U  Q  
P
O calor é chamado
QP ,
pois é trocado a pressão
constante.
Transformação Isotérmica: T = cte
A temperatura não varia em uma transformação
desse tipo. Assim temos que: U  0 , pois a variação da energia interna é função apenas da variação da
temperatura. Assim, aplicando a 1ª Lei da Termodinâmica temos:
Q 
Então, à medida que o gás recebe calor de uma
fonte, ele deve se expandir a fim de realizar um trabalho de igual módulo de energia.
Nesta transformação ABCD horária, temos 4
transformações:
AB  Expansão Isobárica
BC  Isocórica com diminuição da pressão
CD  Contração Isobárica
DA  Isocórica com aumento de pressão
O trabalho total é a soma dos trabalhos realizados nas quatro transformações:


BC
ciclo
  AB   BC   CD   DA
Para o ciclo da figura acima, temos que:
(pois não há variação de volume)
  DA  0
e, portanto, o trabalho total no ciclo é dado por
que é numericamente igual à área


Transformação Adiabática: Q = 0

Numa transformação adiabática não há troca de
calor com o meio externo. Assim, desde que Q  0 ,
temos:
delimitada pelo ciclo, pois somamos a área embaixo de
AB (expansão) e diminuímos a área embaixo de CD
(compressão). Preste atenção: usamos que
0
U  
ciclo

AB

CD

Assim, num ciclo horário, temos
CD
 ciclo  0 . Nes-
se caso o sistema recebe calor e o transforma em trabaImportante: numa expansão adiabática, temperatura e lho.
pressão diminuem, enquanto que numa compressão
Analogamente, num ciclo anti-horário temos
adiabática, temperatura e pressão aumentam. Basta


0 . Desse modo, o trabalho é realizado sobre
analisar a expressão acima junto com a Lei Geral dos ciclo
Gases Perfeitos. Veja abaixo o gráfico de uma expan- o sistema e é convertido em calor.
são adiabática (1-2):
__________________________________________________________________________________________________________________
240
Física - Termodinâmica
CASD Vestibulares
Rendimento de um ciclo
É a razão entre o trabalho útil e a quantidade
de calor fornecida ao sistema.


util
Qfornecido
2ª Lei da Termodinâmica
Processo irreversível: Transformação na qual um
sistema, uma vez atingido o estado final de equilíbrio,
não retorna ao estado inicial ou a quaisquer estados
intermediários, sem a ação de agentes que modifiquem o meio externo (trabalho).
Processo reversível: Transformação que pode ocorrer em ambos os sentidos, passando por todas as etapas intermediárias, sem que isso cause modificações
definitivas ao meio externo.
Entropia (S)
É uma grandeza que mede a degradação da
energia organizada (trabalho) para uma energia desorganizada (térmica). É fundamental para se determinar
a reversibilidade dos processos.
Nos processos naturais, irreversíveis (como
uma pedra caindo no chão), a entropia aumenta, pois a
energia potencial gravitacional da pedra (energia organizada) é degradada em calor.
S  0
Para processos isotérmicos
reversíveis te-
mos:
S 
Q
T
Q1  Calor fornecido pela Fonte Quente
Q2  Calor rejeitado à Fonte Fria
  Trabalho útil fornecido
Da 1ª Lei obtemos que:
 Q Q
1
2
Rendimento de uma Máquina Térmica
Como uma máquina térmica opera em ciclos,
então seu rendimento é igual ao trabalho útil dividido
pelo calor fornecido:

Q1  Q2
Q
1 2
Q1
Q1
Máquinas Frigoríficas
São máquinas térmicas que transferem calor de
uma fonte térmica fria para uma outra mais quente. Para
isso, é claro, é necessária a realização de um trabalho
externo. Veja esquema:
Enunciados da 2ª Lei
1. “A entropia do Universo sempre aumenta”
2. “É impossível construir um dispositivo que, operando
em um ciclo termodinâmico converta totalmente calor e
trabalho, ou seja, com rendimento 100%”.
3. “É impossível a construção de um dispositivo que,
sem a intervenção do meio exterior, consiga transferir
calor de um corpo para outro a temperatura mais elevada”.
O 1º enunciado condiz com o fato já apresentado de que a entropia, em processos naturais, irreversíveis, sempre aumenta. O 2º nega a existência de um
motor ideal. Já o 3º, devido a Clausius, nega a existência de um refrigerador ideal.
A fonte fria deve se localizar no espaço onde se
deseja refrigerar, retirando calor. Enquanto isso, a fonte
quente deverá rejeitar o calor para o meio externo. Desse modo, ao contrário das máquinas térmicas “normais”,
as máquinas frigoríficas convertem trabalho em calor.
Ciclo de Carnot
Máquinas Térmicas
Sadi Carnot, engenheiro francês, estabeleceu um
ciclo
termodinâmico cujo rendimento seria máximo. Veja
Máquinas Térmicas são dispositivos que, trabao
diagrama
PxV do Ciclo de Carnot abaixo:
lhando com duas fontes térmicas, fazem a conversão
entre calor e energia mecânica (trabalho). Veja o esquema abaixo:
__________________________________________________________________________________________________________________
CASD Vestibulares
Física - Termodinâmica
241
Resolução:
02. Uma amostra de gás recebe 500 J na forma de calor
e transfere 200 J ao meio sob a forma de trabalho.
a) Qual a variação na energia interna?
b) O gás aquece ou resfria?
c) O gás expande ou comprime?
Resolução:
Novamente, o trabalho é igual à área delimitada
pelo ciclo (ciclo horário). Temos neste ciclo, 4 transformações:
ab  Expansão isotérmica reversível, onde o sistema
recebe calor da fonte quente (Qa).
bc  Expansão adiabática reversível, onde não há troca de calor (Q=0) com as fontes térmicas.
cd  Compressão isotérmica reversível, onde o sistema cede calor à fonte fria (Qb).
da  Compressão adiabática reversível, onde não há
troca de calor (Q=0) com as fontes térmicas.
03. Em uma transformação adiabática, 1 mol de certo
gás teve sua temperatura aumentada de 20ºC para 50ºC.
Dado: R = 8,31J/mol.K
a) O gás recebeu ou realizou trabalho?
b) Aumentou de volume?
c) Teve sua pressão aumentada?
O grande mérito de Carnot foi relacionar as quanti- Resolução:
dades de calor Q1 e Q2 com as respectivas temperaturas absolutas, da seguinte forma:
Relação de Carnot:
Q1 T1

Q2 T2
Desse modo, o rendimento de uma máquina
Carnot é dado por:
de
T2
T1
04. Uma amostra de gás perfeito é submetida ao ciclo
de transformações indicado no diagrama da figura abaimax
xo:
a) Calcule o trabalho, a variação da energia interna e o
T1  temperatura absoluta (K) da fonte quente
calor trocado de A até B, de B até C e de C até A.
T2  temperatura absoluta (K) da fonte fria
b) Calcule o trabalho, a variação da energia interna e o
Desse modo, uma máquina terá rendimento máxi- calor trocado no ciclo.
mo se, e somente se, operar em um ciclo de Carnot.

1
Exercícios de Sala
01. Calcule o trabalho realizado na transformação gasosa A-B dada abaixo.
__________________________________________________________________________________________________________________
242
Física - Termodinâmica
CASD Vestibulares
Resolução:
forma podemos concluir que o gás sofre uma transformação isobárica.
a) A variação de volume sofrida pelo fluido é somente
devido a sua variação de temperatura, uma vez que a
pressão se mantém constante, portanto,
V 
V
  3T  T  
2
V  V  T
b) )Para uma transformação qualquer, sendo o gás monoatômico, temos:
U 
3
3
nRT  U  nR  3T  T 
2
2

U  3nRT
05. Uma máquina térmica ideal, operando sob o ciclo de 
Carnot, converte uma quantidade de energia igual a 800
J em trabalho útil, por ciclo. A máquina trabalha com c) Para uma transformação isobárica, o trabalho realizado pelo gás é dado por
fontes térmicas a 400 K e 500 K. Determine:
a) O rendimento máximo da máquina.
 gas  P V (I)
b) A quantidade de calor retirada da fonte quente.
c) A quantidade de calor rejeitada à fonte fria.
Da Lei geral dos gases ideais (equação de estado de
um gás ideal)
Resolução:
PV  nRT
temos, para uma transformação isobárica, que
P V  nRT
(II)
Usando a eq. (II) na eq. (I)), obtemos
 gas  nRT
Exercícios Resolvidos
01. Um fluido e n mols de um gás ideal monoatômico
estão no interior de um cilindro provido de um êmbolo
de massa m que pode deslizar livremente sem atrito. O
coeficiente de dilatação térmica do fluido é γ. O êmbolo
e as paredes do recipiente são adiabáticas, exceto a
base, que está em contato com um reservatório térmico.
Inicialmente, o fluido e o gás ocupam, cada um, a metade do volume interno V do cilindro e estão em equilíbrio
com o reservatório à temperatura T. A temperatura do
reservatório é, então, muito lentamente, levada da temperatura inicial T até a temperatura final 3T. Durante
esse processo, o fluido e o gás estão sempre em equilíbrio térmico com o reservatório. Desprezando a dilatação do recipiente e uma possível evaporação do fluido,
determine:
a) a variação do volume do fluido;
b) a variação da energia interna do gás;
c) o trabalho realizado pelo gás.
Resolução:
Uma vez que o êmbolo tem
massa constante e considerando
a pressão externa (atmosférica)
também constante, a força exercida pelo gás sobre o êmbolo é
constante (processo quase estático, equilíbrio). Como a área do
êmbolo não varia, a pressão do
gás permanece constante. Desta

 gas  2nRT
02. Um gás ideal passou do estado A para o estado B,
5
como mostra o gráfico abaixo. Sabendo que 1atm = 10
Pa. Determine:
a) o trabalho realizado pelo gás nessa transformação.
b) a variação da energia interna do gás sabendo que
durante o processo o gás recebe 4000J
P(atm)
B
4,0
2,0
A
2
0
10
V(L)
Resolução:
a) Lembrando que para um diagrama PxV, o trabalho de
um gás é dado pela área abaixo da reta, podemos verificar que a figura geométrica é um trapézio. Assim:

( B  b).h

2
5

(4,0  2,0).8
 24atm.L
2
Como 1atm = 10 Pa e 1L = 10
–3
m³, temos:
  24.10 J
2
Lembrando que as unidades Pa e m³ são do SI, por isso
a unidade de trabalho será o Joule.
b)
Com
o
cálculo
do
trabalho
obtivemos
  24.10 2 J  2400 J
e o calor recebido é de
__________________________________________________________________________________________________________________
CASD Vestibulares
Física - Termodinâmica
243
Q  4000 J , podemos então determinar a variação da 08) A variação da energia interna de um sistema termoenergia interna aplicando a 1ªLei da Termodinâmica.
U  Q  

U  4000  2400 
U  1600 J
Observação: CP e CV são denominados calores molares à pressão e a volume constante, respectivamente.
Sua unidade é cal/mol.K. Eles aparecem nos calores
trocados em transformações isobáricas e isocóricas.
Existe uma relação entre CP e CV, chamada relação de
Meyer. Segundo essa relação, que pode ser facilmente
demonstrada, temos:
CP  CV  R
Exercícios
 Nível 1
dinâmico é dada pela diferença entre a energia trocada
com a vizinhança, na forma de calor, e o trabalho realizado pelo sistema, ou sobre o sistema.
16) O motor de combustão interna de um automóvel não
é uma máquina térmica, porque não opera entre uma
fonte quente e uma fonte fria em ciclos.
32) Um refrigerador funciona como uma máquina térmica, operando em sentido inverso, isto é, retira calor da
fonte fria e, através de trabalho realizado sobre ele,
rejeita calor para a fonte quente.
64) Uma máquina térmica operando segundo o ciclo de
Carnot obtém rendimento de 100%, isto é, converte todo
o calor recebido em trabalho.
06. (FAAP) Numa expansão isobárica, sob pressão de
2
3
10 N/m , a variação de volume do gás é de 3 m . Sabendo-se que durante a transformação ele recebeu 75 J
de calor, calcule a variação de energia interna.
01. (VUNESP) A 1ª lei da termodinâmica diz respeito à:
a) Dilatação térmica
b) Conservação da massa
c) Conservação da quantidade de movimento
d) Conservação da energia
e) Irreversibilidade do tempo
07. (MACK) Um motor térmico funciona segundo o ciclo
de Carnot. A temperatura da fonte quente é 400 K e a
da fonte fria é 300 K. Em cada ciclo o motor recebe 600
cal da fonte quente. A quantidade de calor rejeitada para
a fonte fria em cada ciclo e o rendimento do motor valem, respectivamente:
a) 400 cal e 50%
d) 450 cal e 50%
02. (VUNESP) Uma geladeira retira, por segundo, 1000
b) 300 cal e 25%
e) 450 cal e 25%
kcal do congelador, enviando para o ambiente 1200
c) 600 cal e 50%
kcal. Considere 1 kcal = 4,2 kJ. A potência do compressor da geladeira vale:
08. (FATEC) Um sistema termodinâmico recebe, sob
a) 700 kW
b) 800 kW
c) 840 kW
forma de calor, 600J, enquanto realiza trabalho de 400J.
d) 600 kW
e) 500 kW
A variação de sua energia interna é, neste caso:
a) 200J
b) 600J
c) 400J
3
03. (PUC-RS) Um gás que possui 1.10 J de energia
d) 1000J
e) nula
2
interna, recebe 3.10 J de calor e simultaneamente é
comprimido, realizando-se sobre ele um trabalho mecâ09. (FESP) Um corpo evolui de um estado A a outro B,
2
nico igual a 6.10 J. No final deste processo, a energia
recebendo 100J em trabalho e cedendo 80J em calor.
interna do gás é:
Nestas condições podemos afirmar que a energia inter3
3
3
a) 1,9.10 J
b) 1,6.10 J
c) 1,4.10 J
na do corpo:
3
3
d) 1,3.10 J
e) 1,0. 10 J
a) aumentou 180J b) diminuiu 180J c) aumentou 20J
d) diminuiu 20J
e) n.r.a
04. (FUVEST) Certa quantidade de um gás perfeito
sofre três transformações sucessivas: A  B; B  C; C
10. (FAAP) Um sistema recebe 400 cal de uma fonte
 A, conforme indica o diagrama PxV. Sejam T AB, TBC,
térmica, enquanto ao mesmo tempo é realizado sobre o
TCA, os trabalhos realizados pelo gás em cada uma
sistema um trabalho equivalente a 328J. Qual o aumendaquelas transformações. Podemos afirmar:
to da energia interna do sistema, em Joules? Dê sua
resposta em joules.
a) TAB = 0
Dado: 1 cal = 4,18 J
b) |TCA| > |TAB|
c) TBC = 0
11. (FATEC) Um sistema termodinâmico recebe calor
d) |TBC| > |TAB|
cedido por 100 g de água, que sofre abaixamento de 5
e) TAB +TBC +TCA = 0
0
C em sua temperatura. O sistema, então, se expande
realizando um trabalho de 1240 J = 300 cal. A variação
de energia interna do sistema, nestas condições, é de:
a) 300 cal
b) 800 cal
c) 500 cal
d) 200 cal
e) 1000 cal
05. (UFSC) Assinale a(s) proposições corretas:
01) Sempre que um gás recebe calor, sua temperatura
12. (VUNESP) Transfere-se calor a um sistema, num
sobre um acréscimo.
total de 200 calorias. Verifica-se que o sistema se ex02) Em uma transformação isotérmica o sistema não
pande, realizando um trabalho de 150 joules, e que
troca calor com o meio externo.
sua energia interna aumenta.
04) Numa compressão adiabática, a temperatura do
a) Considerando 1 cal = 4J, calcule a quantidade de
sistema aumenta.
energia transferida ao sistema, em joules.
__________________________________________________________________________________________________________________
244
Física - Termodinâmica
CASD Vestibulares
b) Utilizando a primeira lei da termodinâmica, calcule a
variação da energia interna desse sistema.
13. (UFPA) A 2ª Lei da termodinâmica pode ser encarada como um princípio de degradação da energia, por
quê?
a) O calor não pode passar espontaneamente de um
corpo para outro de temperatura mais baixa que o
primeiro.
b) Para produzir trabalho continuamente, uma máquina
térmica, operando em ciclos, deve necessariamente
receber calor de uma fonte fria e ceder parte dele a
uma fonte quente.
c) É possível construir uma máquina, operando em
ciclos, cujo único efeito seja retirar calor de uma fonte
e convertê-lo totalmente em trabalho
d) É impossível se converter totalmente calor em outra
forma de energia.
e) A termodinâmica independe de qualquer teoria atômico molecular.
a) II e III
d) I e VII
b) III e IV
e) III e VI
c)III e V
18. (ITA) Uma certa massa de gás ideal realiza o ciclo
ABCD de transformações, como mostrado no diagrama
PxV da figura. As curvas AB e CD são isotermas. Podese afirmar que:
a) O ciclo ABCD corresponde a um ciclo de Carnot
b) O gás converte trabalho em calor ao realizar o ciclo
c) Nas transformações AB e CD o gás recebe calor
d) Nas transformações AB e BC a variação da energia
14. (PUC) O rendimento de uma máquina térmica:
interna do gás é negativa
a) depende apenas da temperatura da fonte quente.
e) Na transformação DA o gás recebe calor, cujo valor é
b) é tanto maior quanto maior a diferença de temperatu- igual à variação da energia interna.
ras das fontes quente e fria.
c) depende apenas da temperatura da fonte fria.
 Nível 2
d) não depende das temperaturas das fontes e sim das
transformações envolvidas.
01. (UNICAMP) Uma usina que utiliza a energia das
e) nunca pode ultrapassar a 30%.
ondas do mar para gerar eletricidade opera experimen15. (SANTA CASA) Uma máquina térmica executa um
ciclo entre as temperaturas 500 K (fonte quente) e 400
K (fonte fria). O máximo rendimento que se essa máquina poderá ter, será:
a) 10
b) 20%
c) 25%
d) 30%
e) 80%
16. (ITA) Uma máquina térmica reversível opera entre
dois reservatórios térmicos de temperaturas 100°C e
127°C, respectivamente, gerando gases aquecidos
para acionar uma turbina. A eficiência dessa máquina
é melhor representada por:
a) 68%
b) 6,8%
c) 0,68%
d) 21%
e) 2,1%
talmente na Ilha dos Picos, em Açores. Ela tem capacidade para suprir o consumo de até 1000 pessoas e o
projeto vem sendo acompanhado por cientistas brasileiros. A usina é formada por uma caixa fechada na parte
superior e parcialmente preenchida com a água do mar,
que entra e sai por uma passagem (vide figura), mantendo aprisionada uma certa quantidade de ar. Quando
o nível da água sobe dentro da caixa devido às ondas, o
ar é comprimido, acionando uma turbina geradora de
eletricidade. A área da superfície horizontal da caixa é
2
igual a 50 m .
a) Inicialmente, o nível da água está a 10 m do teto e a
pressão do ar na caixa é igual à pressão atmosférica
5
(10 Pa). Com a saída para a turbina fechada, qual
será a pressão final do ar se o nível da água subir
17. (ITA) Nas afirmações a seguir:
2,0m? Considere que no processo a temperatura do ar
I – A energia interna de um gás ideal depende só da permanece constante.
pressão.
b) Esboce a curva que representa o processo do item
II – Quando um gás passa de um estado 1 para o outro a) em um diagrama de pressão em função do volume
estado 2, o calor trocado é o mesmo qualquer que seja do ar.
o processo.
III – Quando um gás passa de um estado 1 para o outro c) Estime o trabalho (em Joules) realizado pelas ondas
2, a variação da energia interna é a mesma qualquer sobre o ar da caixa.
que seja o processo.
IV – Um gás submetido a um processo quase-estático
não realiza trabalho.
02. (UNICAMP) Uma máquina térmica industrial utiliza
V – O calor específico de uma substância não depende um gás ideal, cujo ciclo de trabalho é mostrado na figura
do processo como ela é aquecido.
abaixo. A temperatura no ponto A é 400 K.
VI – Quando um gás ideal recebe calor e não há variação de volume, a variação da energia interna é igual ao
calor recebido.
VII – Numa expansão isotérmica de um gás ideal o trabalho realizado é sempre menor do que o calor absorvido.
As duas corretas são:
__________________________________________________________________________________________________________________
CASD Vestibulares
Física - Termodinâmica
245
2
NOTE/ADOTE 1 Pa = 1 pascal = 1N/m Massa de 1 mol
de água: 18 gramas
Calor específico da água: 4000 J/(ºC.kg) Massa específica da água: 1,0 kg/L
5
5
2
Na temperatura de 100ºC e à pressão de 1,00x10 Pa, 1
mol de vapor de água ocupa 30L e o calor de vaporização da água vale 40000J/mol. Determine:
a) O intervalo de tempo tA, em segundos, necessário
para levar a água até a ebulição.
b) O intervalo de tempo tB, em segundos, necessário
para evaporar 0,27 mol de água.
c) O trabalho W, em joules, realizado pelo vapor de
água durante o processo de ebulição.
Utilizando 1 atm = 10 N/m , responda:
a) Qual é a temperatura no ponto C?
b) Calcule a quantidade de calor trocada pelo gás com o
ambiente ao longo de um ciclo.
05. (FUVEST) O gráfico a seguir representa duas transformações sofridas por uma determinada massa de gás
03. (UNICAMP) Com a instalação do gasoduto Brasil- perfeito:
Bolívia, a quota de participação do gás natural na geração de energia elétrica no Brasil será significativamente
ampliada. Ao se queimar 1,0 kg de gás natural obtém-se
7
5,0 x 10 J de calor, parte do qual pode ser convertido
em trabalho em uma usina termoelétrica. Considere
uma usina queimando 7200 quilogramas de gás natural
por hora, a uma temperatura de 1227 ºC. O calor não
aproveitado na produção de trabalho é cedido para um
rio de vazão 5000 l/s, cujas águas estão inicialmente a
27 ºC. A maior eficiência teórica da conversão de calor
em trabalho é dada por: η = 1 - (Tmin/Tmax), sendo Tmin e
Tmax as temperaturas absolutas das fontes fria e quente,
respectivamente, ambas expressas em Kelvin. Considere o calor específico da água, c = 4000 J/kg.ºC.
a) Determine a potência gerada por uma usina cuja efia) Qual foi a variação de temperatura do gás entre o
ciência é metade da máxima teórica.
estado inicial A e o final C?
b) Determine o aumento de temperatura da água do rio
b) Qual a quantidade de calor, em Joules, recebida pelo
ao passar pela usina.
gás na seqüência de transformações de A a C?
04. (FUVEST) Um recipiente cilíndrico contém 1,5L
(litro) de água à temperatura de 40 ºC. Uma tampa,
colocada sobre a superfície da água, veda o líquido e
pode se deslocar verticalmente sem atrito. Um aquecedor elétrico E, de 1800 W, fornece calor à água. O
sistema está isolado termicamente de forma que o
calor fornecido à água não se transfere ao recipiente.
Devido ao peso da tampa e à pressão atmosférica
externa, a pressão sobre a superfície da água perma5
nece com o valor P0 = 1,00x10 Pa. Ligando-se o aquecedor, a água esquenta até atingir, depois de um
intervalo de tempo tA, a temperatura de ebulição
(100ºC). A seguir a água passa a evaporar, preenchendo a região entre a superfície da água e a tampa,
até que, depois de mais um intervalo de tempo tB, o
aquecedor é desligado. Neste processo, 0,27 mol de
água passou ao estado de vapor.
06. (UFSCAR) A figura representa um gás ideal contido num cilindro C fechado por um êmbolo E de área
-4
2
S = 1,0 . 10 m e massa m = 1,0 Kg. O gás absorve
uma determinada quantidade de calor Q e, em conse–2
qüência, o êmbolo sobe 5,0.10 m, livremente e sem
5
vazamento. A pressão atmosférica local é 1,0.10 Pa.
__________________________________________________________________________________________________________________
246
Física - Termodinâmica
CASD Vestibulares
a) Calcule os trabalhos realizados pelo gás contra a b) Representar todas as transformações do gás num
pressão atmosférica, a, e contra a gravidade, para diagrama PV e explicar como poderia ser calculado o
calor transferido para o meio ambiente.
2
erguer o êmbolo, g. (Adote g = 10 m/s ).
b) Qual a quantidade mínima de calor que o gás deve 11. (UFES) A figura mostra um recipiente contendo uma
ter absorvido nessa transformação? Que lei física fun- massa m de água, munido de um cilindro com pistão,
contendo esse cilindro n mols de um gás ideal monoadamenta sua resposta? Justifique.
tômico. As paredes do recipiente, o pistão e as paredes
07. (ITA) Um recipiente cilíndrico vertical é fechado por laterais do cilindro são adiabáticos, enquanto a base do
2
meio de um pistão, com 8,00 kg de massa e 60,0 cm cilindro é feita de material condutor. Inicialmente, a água
de área, que se move sem atrito. Um gás ideal, contido e o gás estão em equilíbrio térmico à temperatura T0,
o
o
no cilindro, é aquecido de 30 C a 100 C, fazendo o com o gás ocupando um volume V do cilindro. O gás é
pistão subir 20,0 cm. Nesta posição, o pistão é fixado, lentamente comprimido até ocupar um volume V/2 do
enquanto o gás é resfriado até sua temperatura inicial. cilindro. Considere-se que a constante dos gases ideais
Considere que o pistão e o cilindro encontram-se expos- é R. Sendo a temperatura final de equilíbrio igual a T,
tos à pressão atmosférica. Sendo Q1 o calor adicionado determine:
ao gás durante o processo de aquecimento e Q 2, o calor a) a pressão final do gás.
retirado durante o resfriamento, assinale a opção correta b) o trabalho realizado sobre o gás durante a compressão.
que indica a diferença Q1 – Q2.
a) 136 J
b) 120 J
c) 100 J
d) 16 J
e) 0 J

08. (IME) Ao analisar o funcionamento de uma geladeira
de 200 W, um inventor percebe que a serpentina de
refrigeração se encontra a uma temperatura maior que a
ambiente e decide utilizar este fato para gerar energia.
Ele afirma ser possível construir um dispositivo que opere em um ciclo termodinâmico e que produza 0,1 hp.
Baseado nas Leis da Termodinâmica discuta a validade
da afirmação do inventor. Considere que as temperatuGABARITO
ras da serpentina e do ambiente valem, respectivamente, 30°C e 27°C. Suponha também que a temperatura
Nível 1
no interior da geladeira seja igual a 7°C.
Dado: 1 hp = 0,75 kW
01. d 02. c 03. a 04. d 05. 44
06. ∆U = 45 J 07. e 08. a 09. c
09. (IME) Um cilindro contém oxigênio à pressão de 2
10. ∆U = 2000 J 11. d
atmosferas e ocupa um volume de 3 litros à temperatura
12. a) Q = 800 J b) U = 650 J
de 300 K. O gás, cujo comportamento é considerado
13. d 14. b 15. b
ideal, executa um ciclo termodinâmico através dos se16. b 17. e 18. e
guintes processos:
1-2: aquecimento a pressão constante até 500 K.
2-3: resfriamento a volume constante até 250 K.
Nível 2
3-4: resfriamento a pressão constante até 150 K.
4-1: aquecimento a volume constante até 300 K.
5
01. a) Pf = 1,25.10 Pa
b)
Ilustre os processos em um diagrama pressão-volume e
determine o trabalho executado pelo gás, em Joules,
durante o ciclo descrito acima. Determine, ainda, o calor
líquido produzido ao longo deste ciclo. Dado: 1 atm =
5
10 Pa.
2
10. (OBF) O êmbolo de uma seringa tem área de 1 cm ,
massa e atrito desprezíveis. O êmbolo é recuado de
3
forma que a seringa aspira 5 cm de ar a 27 ºC (temperatura ambiente) e pressão atmosférica normal (1 atm) .
A seringa é colocada verticalmente, com o bico para
baixo, sobre uma mesa emborrachada que veda totalmente o bico. Quando uma massa de 4 kg é colocada
sobre o êmbolo, verifica-se que imediatamente após, o
3
7
volume se reduz a 1,7 cm . Depois de cerca de 20 minuc) W = 1,125 X 10 J
tos a massa é retirada de cima do êmbolo muito lentamente. (O êmbolo é descomprimido durante cerca de 30
02. a) TC = 1200 K
min).
4
b) Q = 5.10 J
a) Calcular o volume do ar depois de cerca de 30 min.
7
03. a) P = 4.10 W
b) ΔT = 3 ºC
__________________________________________________________________________________________________________________
CASD Vestibulares
Física - Termodinâmica
247
04. a) tA = 200 s
b) tB = 6,0s
2
J
05. a) ∆T = 0
b) Q = 12 J
06. a) a = 0,5 J; g = 0,5 J
b) Q = 2,5 J; 1ª Lei da Termodinâmica
07. a
08. O refrigerador produz apenas 0,035 hp.
A afirmação do inventor é incorreta.
09. W ciclo = Qciclo = 200 J
3
10. a) VF = 5cm
b) O calor é igual ao trabalho, que é a
área delimitada pelo ciclo.
11. a)
P
b) Wext
2nRT
V
3

  nR  m T  T0 
2

__________________________________________________________________________________________________________________
248
Física - Termodinâmica
CASD Vestibulares