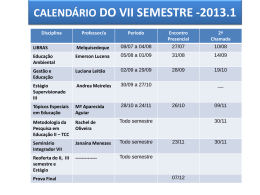
Capítulo 2
Máquinas de Estado
2.1 Introdução
2.2 Estruturas das máquinas de estado
2.3 Máquina de estados finitos
2.4 Máquina de estados não determinísticos
2.5 Equivalência de máquinas de estados
2.6 Composição de máquinas de estados
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
32
2.5 Equivalência de máquinas de estado
– Duas máquinas de estado diferentes, com os mesmos alfabetos,
podem ser equivalentes no sentido em que para a mesma sequência
de entrada produzem a mesma sequência de saída
– Exemplo:
• 3 máquinas com o mesmo alfabeto de entrada e de saída
• A e B produzem uma sequência alternada de 110 quando recebem
uma sequência de 1’s na entrada
• C é não determinística, pode produzir qualquer sequência alternada de
1’s (>0) e um 0
A
B
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
C
33
2.5 Equivalência de máquinas de estado
– Queremos mostrar que a máquina C simula B e A, e que a máquina B é
equivalente a A
– Jogo da simulação com duas máquinas
• As máquinas começam no mesmo estado inicial
• A primeira máquina reage ao símbolo de entrada
– Se a máquina for não determinística existe mais do que uma possível reacção
• A segunda máquina reage ao mesmo símbolo de entrada de modo a
produzir o mesmo símbolo de saída
– Se a máquina for não determinística é livre de escolher das reacções possíveis
qualquer uma que esteja de acordo com o símbolo de saída da primeira
máquina e que permita continuar a gerar os mesmo símbolos de saída
• A segunda máquina simula a primeira máquina se consegue sempre gerar
um símbolo de saída igual ao da primeira máquina
– Se a relação de simulação ocorre em ambos os sentidos então as
máquinas são equivalentes
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
34
2.5 Equivalência de máquinas de estado
• Exemplo: a máquina C simula a máquina B ?
{1} / 1
{1} / 0
aus / aus
{1} / 1
1e4
0
{1} / 1
0e3
C
{1} / 1
B
1-5
2e5
{1} / 0
s0 = ( 0e3 , 0 )
0e3
aus / aus
0
1/1
1/1
0e3
1e4
a/a
1e4
1/1
a/a
2e5
2e5
s1 = ( 1e4 , 1-5 )
0
1-5
a/a
1/0
s2 = ( 2e5 , 1-5 )
0e3
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
1-5
1/1
a/a
1-5
1-5
1/0
0
35
2.5 Equivalência de máquinas de estado
– Exemplo: determinar se C simula B
B
C
• Máquinas nos estados iniciais
S0=(0and3,0) ∈ EstadosB x EstadosC
• A máquina B reage primeiro (está a ser simulada)
S1=(1and4,1to5) ∈ EstadosB x EstadosC
S2=(2and5,1to5) ∈ EstadosB x EstadosC
• Volta a S0 ⇒ C simula B
• A relação de simulação estabelece a correspondência entre as 2 máquinas
SB,C={S0,S1,S2} ⊂ EstadosB x EstadosC
– A simulação é usada para estabelecer uma relação entre um modelo
mais abstracto e um modelo mais detalhado
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
36
2.5 Equivalência de máquinas de estado
–
Estratégia de simulação
•
Suponha-se que temos duas máquinas X e Y definidas por
X=(EstadosX,Entradas,Saídas,PossíveisActualizaçõesX,EstadoInicialX)
e
Y=(EstadosY,Entradas,Saídas,PossíveisActualizaçõesY,EstadoInicialY)
• Y simula X se existe um subconjunto S⊂ EstadosX,x EstadosY tal que
1. (EstadoInicialX,EstadoInicialY)∈S
2. Se (sX(n), sY(n))∈S, então ∀x (n) ∈Entradas, e
∀(sX(n+1), yX(n))∈PossíveisActualizaçõesX(sX(n),x(n)),
existe (sY(n+1), yY(n))∈PossíveisActualizaçõesY(sY(n),x(n)) tal que
1. (sX(n+1), sY(n+1))∈S
2. yX(n)=yY(n)
•
O conjunto S se existir é denominado a relação de simulação,
estabelecendo uma correspondência entre os estados das duas
máquinas
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
37
2.5 Equivalência de máquinas de estado
• Exemplo: a máquina B simula a máquina A ?
A
{1} / 1
0
1/
1
/1
1
1
1
2
/0
/
1
s
2
/1
au
{1} / 1
{1} / 0
a
1
/
0 a
3
/1
/a
1
a
0
1
4
3
/0
a
/
1
a
2 a
5
a/
a
3
{1} / 1
{1} / 0
/
0
a
5
4
4
5
3 1/1
{1} / 1
e
0
/1
s
1
4
u
/0
1e
/a
B
5
1
s
u
2e
a
/1
a
1e4
1
3
/
e3
0e a
/1
/a
{1} / 1
0
1
a
4
e4
1e
/0
1
a
/
5
1
a
{1} / 1
/
2e a
e5
a
2
0e3
3
3
/a
0e
0e
a
4
1e
2e5
{1} / 0
5
2e
s
au
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
38
2.5 Equivalência de máquinas de estado
– Exemplo: determinar se B simula A
A
B
• A relação de simulação é o sub-conjunto
SA,B ⊂ {0,1,2,3,4,5} x {0and3,1and4,2and5}
• A reage primeiro (está a ser simulada)
• Sequência de estados:
SA,B={(0,0and3),(1,1and4),(2,2and5),(3,0and3),(4,1and4),(5,2and5)}
• Conclui-se que B simula A e é fácil de verificar que A simula B
• As máquinas A e B são equivalentes
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
39
2.5 Equivalência de máquinas de estado
• Exemplo: a máquina A simula a máquina B ?
B
1
3
0e 1 /
1
/
{1} / 1
s
1
e4
au
/0
1
/
5
1
s
e
{1} / 1
1
2
au
/
a
1
0e3
3
/
e3
0e a
/1
/a
0
1
a
4
e4
1e
/0
1
a
2e5
/
5
1
a
{1} / 0
/
2e a
e5
a
2
3
/a
e3
0e
0
a
4
1e
5
A
2e
{1} / 1
/1
0
1
1
2
/1
s
1
u
1
/0
/a
{1} / 1
{1} / 0
1
s
2
/1
au
a
1
/
0 a
0
3
/1
/a
3
1
a
1
4
/0
a
/
1
a
2 a
{1} / 1
{1} / 0
5
a/
5
4
a
3
/
0
a
4
{1} / 1
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
5
1e4
40
2.5 Equivalência de máquinas de estado
– A relação de simulação é transitiva
• Mostrámos que C simula B e que B simula A
SB,C ⊂ EstadosB x EstadosC
SA,B ⊂ EstadosA x EstadosB
então
SA,C={(SA,SC) ∈ EstadosA x EstadosC |
∃ SB ∈ EstadosB onde (SA,SB) ∈ SA,B e (SB,SC) ∈ SB,C}
é a relação de simulação que mostra que C simula A
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
41
2.5 Equivalência de máquinas de estado
– Exemplo: aplicação da propriedade transitiva
• B simula A
SA,B={(0,0and3),(1,1and4),(2,2and5),(3,0and3),(4,1and4),(5,2and5)}
• C simula B
SB,C={(0and3,0),(1and4,1to5),(2and5,1to5)}
• Podemos concluir que C simula A
SA,C={(0,0),(1,1to5),(2,1to5),(3,0),(4,1to5),(5,1to5)}
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
42
2.5 Equivalência de máquinas de estado
– Exemplo: determinar se B simula C
C
B
• A relação de simulação é o sub-conjunto
SC,B ⊂ {0,1to5} x {0and3,1and4,2and5}
• C reage primeiro (está a ser simulada)
• Sequência de estados:
SC,B={(0,0and3),(1to5,1and4),...}
• Conclui-se que B não simula C
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
43
Capítulo 2
Máquinas de Estado
2.1 Introdução
2.2 Estruturas das máquinas de estado
2.3 Máquina de estados finitos
2.4 Máquina de estados não determinísticos
2.5 Equivalência de máquinas de estados
2.6 Composição de máquinas de estados
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
44
2.6 Composição de máquinas de estado
– Analisámos os sistemas como funções, logo a composição de sistemas
é uma composição de funções
– Pretendemos definir uma nova máquina de estados que descreve a
composição de várias máquinas de estado
– Vamos trabalhar com composição síncrona, ou seja, cada máquina de
estados na composição reage simultaneamente e instantaneamente
– A reacção da composição consiste num conjunto de reacções
simultâneas de cada uma das máquinas componentes
– Um sistema que reage apenas em resposta a estímulos externos é
denominado de reactivo
– Como a composição é síncrona estes sistemas são denominados de
reactivos síncronos
– As reacções são instantâneas, o símbolo de saída de uma máquina
acontece de uma forma simultânea com o símbolo de entrada
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
45
2.6 Composição de máquinas de estado
• Composição lado-a-lado
(Estados, Entradas, Saídas,Actualização, EstadoInicial)
(EstadosA, EntradasA, SaídasA, ActualizaçãoA, EstadoInicialA)
(EstadosB, EntradasB, SaídasB, ActualizaçãoB, EstadoInicialB)
– As duas máquinas de estado não interferem entre si
– Pretende-se definir uma única máquina de estados representando a
operação síncrona das duas máquinas de estado componentes
– Poderemos desejar que apenas uma máquina reaja
– Se trocarmos a ordem das máquinas obtemos uma máquina
diferente mas equivalente
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
46
2.6 Composição de máquinas de estado
– Definição da composição de máquinas lado-a-lado
•
•
•
•
•
Estados = EstadosA x EstadosB
Entradas = EntradasA x EntradasB
Saídas = SaídasA x SaídasB
EstadoInicial = (EstadoInicialA , EstadoInicialB)
((sA(n+1),sB(n+1)),(yA(n),yB(n)))=Actualização((sA(n),sB(n)),(xA(n),xB(n)))
onde
• (sA(n+1),yA(n))=ActualizaçãoA (sA(n),xA(n))
• (sB(n+1),yB(n))=ActualizaçãoB (sB(n),xB(n))
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
47
2.6 Composição de máquinas de estado
– Exemplo:
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
48
2.6 Composição de máquinas de estado
• Estados = EstadosA x EstadosB = {(1,1),(2,1)}
• Entradas = EntradasA x EntradasB =
{(0,0),(1,0),(nuloA,0),(0,nuloB),(1,nuloB),(nuloA,nuloB)}
• Saídas = SaídasA x SaídasB =
{(a,c),(b,c),(nuloA,c),(a,nuloB),(b,nuloB),(nuloA,nuloB)}
• EstadoInicial = (EstadoInicialA , EstadoInicialB) = (1,1)
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
49
2.6 Composição de máquinas de estado
• Composição em cascata
(Estados, Entradas, Saídas,Actualização, EstadoInicial)
(EstadosA,
EntradasA,
SaídasA,
ActualizaçãoA,
EstadoInicialA)
(EstadosB,
EntradasB,
SaídasB,
ActualizaçãoB,
EstadoInicialB)
– Também designada por ligação em série
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
50
2.6 Composição de máquinas de estado
– Assumpções sobre as máquinas componentes
• SaídasA ⊂ EntradasB
– Definição da composição de máquinas em cascata
•
•
•
•
•
Estados = EstadosA x EstadosB
Entradas = EntradasA
Saídas = SaídasB
EstadoInicial = (EstadoInicialA , EstadoInicialB)
((sA(n+1),sB(n+1)), yB(n))=Actualização((sA(n),sB(n)),x(n))
onde
• (sA(n+1),yA(n))=ActualizaçãoA (sA(n),x(n))
• (sB(n+1),yB(n))=ActualizaçãoB (sB(n),yA(n))
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
51
2.6 Composição de máquinas de estado
– Exemplo
• Estados = EstadosA x EstadosB =
{(0,0),(0,1),(1,0),(1,1)}
• Entradas = Saídas = {0,1,nulo}
• EstadoInicial = (0,0)
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
52
2.6 Composição de máquinas de estado
• Entradas e saídas sob a forma de produto
– Pretende-se modelar a situação em que as entradas são seleccionadas
de partes distintas e as saídas são enviadas para partes distintas
EntradasA
(Estados, Entradas, Saídas,Actualização, EstadoInicial)
SaídasA
EntradasB
Entradas = EntradasA x EntradasB
Saídas = SaídasA x SaídasB
SaídasB
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
53
2.6 Composição de máquinas de estado
– Exemplo
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
54
2.6 Composição de máquinas de estado
• Exemplo
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
55
2.6 Composição de máquinas de estado
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
56
2.6 Composição de máquinas de estado
• Composição para a frente genérica
(Estados, Entradas, Saídas,Actualização, EstadoInicial)
EntradasA
SaídasA2 ⊂ EntradasB1
EntradasB2
SaídasA1
(EstadosA,
EntradasA,
SaídasA,
ActualizaçãoA,
EstadoInicialA)
SaídasA2
(EstadosB,
EntradasB,
SaídasB,
ActualizaçãoB,
EstadoInicialB)
SaídasB
– Exercício: defina a composição das máquinas para este exemplo
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
57
2.6 Composição de máquinas de estado
– Assumpções sobre as máquinas componentes
• SaídasA2 ⊂ EntradasB1
– Definição da composição para a frente genérica
•
•
•
•
•
Estados = EstadosA x EstadosB
Entradas = EntradasA x EntradasB2
Saídas = SaídasA1 x SaídasA2 x SaídasB
EstadoInicial = (EstadoInicialA , EstadoInicialB)
((sA(n+1),sB(n+1)), (yA1(n),yA2(n),yB(n)))=
Actualização((sA(n),sB(n)),(xA(n), xB2(n)))
onde
• (sA(n+1),(yA1(n), yA2(n)))=ActualizaçãoA(sA(n),xA(n))
• (sB(n+1),yB(n))=ActualizaçãoB(sB(n),(yA2(n),xB2(n)))
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
58
2.6 Composição de máquinas de estado
• Composição hierárquica
(Estados, Entradas, Saídas,Actualização, EstadoInicial)
(EstadosA,
EntradasA,
SaídasA,
ActualizaçãoA,
EstadoInicialA)
(EstadosB,
EntradasB,
SaídasB,
ActualizaçãoB,
EstadoInicialB)
(EstadosC,
EntradasC,
SaídasC,
ActualizaçãoC,
EstadoInicialC)
– Diferentes estratégias para composição das máquinas
– Essas estratégias geram máquinas de estado diferentes mas
equivalentes
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
59
2.6 Composição de máquinas de estado
(Estados, Entradas, Saídas,Actualização, EstadoInicial)
(EstadosAB,EntradasAB,SaídasAB,ActualizaçãoAB,EstadoInicialAB)
(EstadosA,
EntradasA,
SaídasA,
ActualizaçãoA,
EstadoInicialA)
(EstadosB,
EntradasB,
SaídasB,
ActualizaçãoB,
EstadoInicialB)
(EstadosC,
EntradasC,
SaídasC,
ActualizaçãoC,
EstadoInicialC)
(Estados, Entradas, Saídas,Actualização, EstadoInicial)
(EstadosBC,EntradasBC,SaídasBC,ActualizaçãoBC,EstadoInicialBC)
(EstadosA,
EntradasA,
SaídasA,
ActualizaçãoA,
EstadoInicialA)
(EstadosB,
EntradasB,
SaídasB,
ActualizaçãoB,
EstadoInicialB)
Sistemas e Sinais - LEIC - 2007/2008 - 2º Semestre - João P. Neto
(EstadosC,
EntradasC,
SaídasC,
ActualizaçãoC,
EstadoInicialC)
60
Download