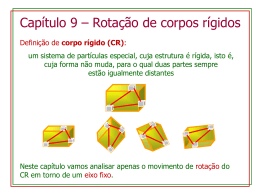
Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Capítulo 9 - Rotação de Corpos Rígidos Aquino Lauri Espíndola 1 1 Departmento de Física Instituto de Ciências Exatas - ICEx, Universidade Federal Fluminense Volta Redonda, RJ 27.213-250 1 de dezembro de 2010 Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Conteúdo 1 Velocidade Angular e Aceleração Angular Velocidade Angular Velocidade Angular como um Vetor Aceleração Angular Aceleração Angular como um Vetor 2 Rotação com Aceleração Angular Constante 3 Relações entre Cinemática Linear e Cinemática Angular Aceleração Linear na Rotação de Um Corpo Rígido 4 Energia no Movimento de Rotação Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Velocidade Angular Velocidade Angular como um Vetor Aceleração Angular Aceleração Angular como um Vetor Velocidade Angular Eixo Fixo: eixo que permanece em repouso em relação a um referencial inercial. O eixo passa através do ponto O ⊥ ao plano do quadro. A linha OP permanece fixa no corpo e gira com ele. O ângulo θ descreve a posição da rotação. θ será coordenada da rotação. A coordenada θ pode ser (+) ou (−). Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Velocidade Angular Velocidade Angular como um Vetor Aceleração Angular Aceleração Angular como um Vetor Velocidade Angular O ângulo θ é medido em radianos, não em graus. r , raio de circunferência. s, comprimento do arco de circunferência. Se o ângulo for 1 rad ⇒ s = r . Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Velocidade Angular Velocidade Angular como um Vetor Aceleração Angular Aceleração Angular como um Vetor Velocidade Angular O valor de θ em radianos é: θ= s r ou s = r θ. O comprimento de uma circunferência é 2πr . Existem 2π radianos em uma revolução completa. 1 rad = Aquino Espíndola 360◦ = 57, 3◦ 2π Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Velocidade Angular Velocidade Angular como um Vetor Aceleração Angular Aceleração Angular como um Vetor Velocidade Angular O movimento de rotação pode ser descrito em termos da taxa de variação do ângulo θ. Em t1 , OP faz um ângulo θ1 . Em t2 , OP faz um ângulo θ2 . Definimo a velocidade angular média: ωm = θ2 − θ1 ∆θ = . t2 − t1 ∆t A rotação ocorre em torno do eixo z. Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Velocidade Angular Velocidade Angular como um Vetor Aceleração Angular Aceleração Angular como um Vetor Velocidade Angular A velocidade angular instantânea:. dθ ∆θ = ω = lim dt ∆t→0 ∆t A velocidade angular ω pode ser (+) ou (−). Rotação no sentido anti-horário (+): ∆θ > 0 ⇒ ωm = ∆θ ∆t Rotação no sentido horário (−): >0 Aquino Espíndola ∆θ < 0 ⇒ ωm = Capítulo 9 - Rotação de Corpos Rígidos ∆θ ∆t <0 Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Velocidade Angular Velocidade Angular como um Vetor Aceleração Angular Aceleração Angular como um Vetor Velocidade Angular Unidade de velocidade angular: rad/s. Outras unidades: Revolução por minuto: rev/min ou rpm. 1 rev = 2π. Conversões úteis: 1 rev/s = 2π rad /s 1 rev/min = 1 rpm = Aquino Espíndola 2π rad /s 60 Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Velocidade Angular Velocidade Angular como um Vetor Aceleração Angular Aceleração Angular como um Vetor Velocidade Angular como Vetor Translação: vx é o componente x do vetor ~v . Rotação: ω é o componente do vetor velocidade ω ~ ao longo do eixo. Qual o sentido de ~ ω? Encurvar os dedos da mão direita no sentido da rotação. Aquino Espíndola Sentidos de ~ω : Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Velocidade Angular Velocidade Angular como um Vetor Aceleração Angular Aceleração Angular como um Vetor Aceleração Angular Se a velocidade angular varia, o corpo possui aceleração angular. Em t1 , o corpo possui ω1 . Em t2 , o corpo possui ω2 . A aceleração angular média: αm = ∆ω ω2 − ω1 = t2 − t1 ∆t A aceleração angular instantânea: dω ∆ω = dt ∆t→0 ∆t α = lim Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Velocidade Angular Velocidade Angular como um Vetor Aceleração Angular Aceleração Angular como um Vetor Aceleração Angular como Vetor Translação: ax é o componente x do vetor ~a. Rotação: α é o componente do vetor aceleração α ~ ao longo do eixo. α ~ e ~ω no mesmo sentido: a rotação é acelerada. Aquino Espíndola α ~ e~ ω em sentidos opostos: a rotação é retardada. Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Rotação com α = cte Em t = 0, o corpo possui velocidade angular ω0 . Em um t qualquer, a velocidade angular será ω. Assim, neste intervalo de tempo: α= ω − ω0 t −0 ou Somente para α = cte ω = ω0 + αt Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos (1) Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Rotação com α = cte Outra equação já conhecida: ωm = ω0 + ω . 2 (2) θ − θ0 . t −0 (3) Também sabemos que: ωm = Igualando as Equações (2) e (3) e multiplicando-as por t: Somente para α = cte θ − θ0 = Aquino Espíndola 1 (ω0 + ω) . 2 Capítulo 9 - Rotação de Corpos Rígidos (4) Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Rotação com α = cte Substituindo a Eq. (1) na Eq. (4): Somente para α = cte 1 θ = θ0 + ω0 t + αt 2 . 2 (5) Relacionando as grandezas translacionais com as grandezas rotacionais: Somente para α = cte ω 2 = ω02 + 2α∆θ . Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos (6) Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Aceleração Linear na Rotação de Um Corpo Rígido Relação Grandezas de Translação e Rotação Movimento Retílineo com Aceleração Constante Rotação com Aceleração Constante a = constante α = constante v = v0 + at ω = ω0 + αt x = x0 + v0 t + 12 at 2 θ = θ0 + ω0 t + 21 αt 2 v 2 = v02 + 2a∆x ω 2 = ω02 + 2α∆θ x − x0 = 12 (v + v0 )t θ − θ0 = 12 (ω + ω0 )t Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Aceleração Linear na Rotação de Um Corpo Rígido Cinemática Linear e Angular Como achar a velocidade linear e a aceleração um dado ponto em um corpo girando? Cada partícula se move em uma trajetória circular. O círculo fica sobre um plano ⊥ ao eixo. O círculo possui centro no eixo. A velocidade da partícula é diretamente proporcional a velocidade angular. Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Aceleração Linear na Rotação de Um Corpo Rígido Velocidade Linear na Rotação Relação entre ângulo e comprimento de arco: s = r θ. Derivando a equação acima em relação ao tempo: ds = r dθ . dt dt |ds/dt| é a taxa de variação do comprimento de arco. |d θ/dt| é a taxa de variação ângulo. Portanto: v = rω . Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Aceleração Linear na Rotação de Um Corpo Rígido Aceleração Linear na Rotação Uma partícula girando: aceleração centrípeta ou radial, arad , aceleração tangencial, atg . atg é paralela a v, portanto, altera o módulo de v. Sabemos que atg = dv/dt. Derivando a expressão v = ωr : atg = dω dv =r = rα dt dt Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Aceleração Linear na Rotação de Um Corpo Rígido Aceleração Linear na Rotação Uma partícula girando: aceleração centrípeta ou radial, arad , aceleração tangencial, atg . arad aponta em direção ao centro e modifica direção de v. Sabemos que arad = v 2 /r . Sabemos que v = ωr , então: arad = Aquino Espíndola v2 = ω2r r Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Aceleração Linear na Rotação de Um Corpo Rígido Aceleração Linear na Rotação Atenção: Usar grandezas angulares somente em radianos!!! Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Energia no Movimento de Rotação Um corpo rígido é constituído por: grande número de partículas com massas m1 , m2 , . . ., partículas estãoà distância do centro r1 , r2 , . . ., a i−ésima partícula: mi e ri . Quando um corpo rígido gira: a i−ésima partícula tem velocidade vi = ri ω; onde ω é a velocidade angular do corpo. Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Energia no Movimento de Rotação A energia cinética da i−ésima partícula: 1 1 mi vi2 = mi ri2 ω 2 . 2 2 A energia cinética total do corpo é: K = 1 1X 1 m1 r12 ω 2 + m2 r22 ω 2 + . . . = mi ri2 ω 2 2 2 2 i Colocando em evidência o termo ω 2 /2: ! 1 X 1 2 2 2 2 m1 r1 + m2 r2 + . . . ω = mi ri ω 2 K = 2 2 i Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Energia no Movimento de Rotação A grandeza entre parênteses é denominada momento de inércia, I Momento de Inércia em Relação a um Eixo X I = m1 r12 + m2 r22 + . . . = mi ri2 i A energia cinética de rotação da por: ! 1 X 2 mi ri ω 2 K = 2 i Pode ser reescrita como: K = Aquino Espíndola 1 2 Iω 2 Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Momento de Inércia Massa próxima ao eixo. Massa distante do eixo. Menor momento de inércia. Maior momento de inércia. Fácil fazer girar. Difícil fazer girar. Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos Velocidade Angular e Aceleração Angular Rotação com Aceleração Angular Constante Relações entre Cinemática Linear e Cinemática Angular Energia no Movimento de Rotação Momento de Inércia: Exemplos Aquino Espíndola Capítulo 9 - Rotação de Corpos Rígidos
Download