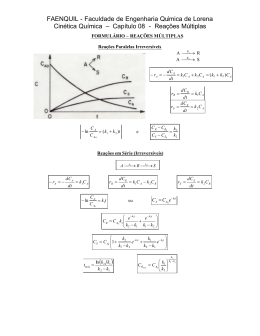
!
"
#
"
#
#
"
#
!
"
(
,
)
.
-
* +*
+
/ #
#
*
%
%
=
=
$
&
=
&
%
=
'
=
0 +
=
0
=0
0
=
'
=
0 +
=
0
&
=
0
1
+
&
+&
(
&
+
&
0
−
0
)
#
"
% 3
"
#
2%$
$
4
.
$
5
2%
$3
5
%
5
%
5
%
5
=
+
5
=
+
5
=
+
56
56
56
/
&
"
"
#
7 8
:
=
+
+
+
.
=
=
+
9
#
•
4
=
••
=
/
•
••
7 8
=
•
=
••
!
'
"
+
#
=
+
&
=
=
;
*
+
ρ
8
&
=
;
!
*
8
(
%
.
0 < &= 6
α = 1− (
.
#
α)
&A
= 1−
&=
&
5
;
&B #
&A
− 1A = 0 + &= × 1 −
&=
9
*
4
= @ ?1 6
=
0
+
0
+
0
= >& & 6
&
9
!
0
−
−
= 1 C&@
&
4
=
&
= 1 0=?
. #
'
7
1
&
&
⇔
&A = 0 + &=
− 1A = 0 + &=
α=
&A
&=
α
α −
1
&
&
/
#
α = D 0@B
α = A& @B
4
4
1
&
&
&
%
'
!
#
θ < &0
7 8
. .
A000
#
CA0 6. .
)
$
E< A000
( ) = 1@A CD@
(
− C1 &A=
6
( ) = ( (1@A CD@
+
&
= ( 0 ) + ( −@ ?1 6
0
0
=
0
=
+ A000
− ( C1 &A=
− ( C1 &A=
6
)
− ( = @0A
+ 1= A&C − 10&0 =0? = 0
=
−1= A&C ±
(1= A&C )
&
− = ( −10&0 =0? )
&
−1= A&C ± DA A1?
=
= &A A
&
1000
1F
6
+
0
( &0 )
. .
− C1 &A=
6
*
= (1@A CD@
6
&
))
6
#
6
( &0 )
= 1@A CD@
)
>D00
= CA0 F 6= &0? >>
&
))
. .
A000
. .
= * + E
6
6 + ( @ ?1 6
)( &A A ) = =@@1
6
&
)
&
=0
)
− ( @ ?1 6
&
&
)&
)
%
*
C 1! '
>00
C &! '
9
7
?
1A 6
&C 6
>
#
8
&0 6
#
*
C &! 9
.
#
5
.
9 9
.
#
:
.
#
#
6
. α = =AB
5
#
#
:
-
#
.
!
-
-
!
5
#
2≅
3
9
+
C =G '
D=
C DG $ * !
$
=C
9
'
&? @
=>
3
.3
3
/
C>
#
#
#
>=0
#
:
# .
#
;:@D
%
%
&
;: 30 D0
.30 00@=
C AG '
.
#
4
30 CC
!
/
H
@00
D
$
1==
!
8
.
D
.3& =
&A0
4
0D
8
@D
:
#
;: 3G& &
C C! '
8
.
3
.3
$
!
3
.3
;: 30 =A
,
0 CA
:
%
#
.31C C