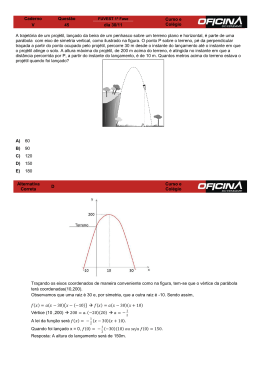
1. (Ufsm 2015) Uma pesquisa do Ministério da Saúde
revelou um aumento significativo no número de obesos no
Brasil. Esse aumento está relacionado principalmente com o
sedentarismo e a mudança de hábitos alimentares dos
brasileiros. A pesquisa divulgada em 2013 aponta que
17% da população está obesa. Esse número era de 11%
em 2006, quando os dados começaram a ser coletados pelo
Ministério da Saúde.
Disponível em: http://www.brasil.gov.br/saude/2013/08/obesidade-atinge-maisda-metade-dapopulacao- brasileira-aponta-estudo. Acesso em: 10 set. 2014.
Suponha que o percentual de obesos no Brasil pode ser
expresso por uma função afim do tempo t em anos, com
t  0 correspondente a 2006, t  1 correspondente a 2007
e assim por diante.
A expressão que relaciona o percentual de obesos Y e o
tempo t, no período de 2006 a 2013, é
4
44
t.
3
3
7
77
Y= t .
6
6
Y = t  11.
6
Y = t  11.
7
3
Y = t  11.
4
a) Y = t 
b)
c)
d)
e)
realizou 10 corridas e arrecadou R$ 410,00, então a
média de quilômetros rodados por corrida, foi de
a) 14
b) 16
c) 18
d) 20
4. (Unesp 2015) A tabela indica o gasto de água, em m3
por minuto, de uma torneira (aberta), em função do quanto
seu registro está aberto, em voltas, para duas posições do
registro.
Abertura da torneira
(volta)
0,5
1
(m3 )
0,02
0,03
(www.sabesp.com.br. Adaptado.)
Sabe-se que o gráfico do gasto em função da abertura é
uma reta, e que o gasto de água, por minuto, quando a
torneira está totalmente aberta, é de 0,034 m3 . Portanto, é
correto afirmar que essa torneira estará totalmente aberta
quando houver um giro no seu registro de abertura de 1
volta completa e mais
a)
2. (G1 - cftmg 2015) Um estudante de engenharia faz b)
trabalhos de digitação para complementar seu ganho
mensal. Ele estabelece que a relação entre o preço P e a c)
quantidade q de páginas de cada trabalho é dada pela
função P(q)  aq  b, sendo a e b números reais d)
positivos, e
Gasto de água por minuto
q pertencente ao intervalo 1  q  100.
Sabendo-se que o conjunto imagem dessa função é o e)
intervalo 6  P(q)  105, o estudante calcula os valores de
1
2
1
5
2
5
3
4
1
4
de volta.
de volta.
de volta.
de volta.
de volta.
a e b. Desse modo, a média aritmética entre a e b é 5. (Uel 2015) ViajeBem é uma empresa de aluguel de
veículos de passeio que cobra uma tarifa diária de
igual a
R$ 160,00 mais R$ 1,50 por quilômetro percorrido, em
a) 1,5
b) 2,0
carros de categoria A. AluCar é uma outra empresa que
cobra uma tarifa diária de R$ 146,00 mais R$ 2,00 por
c) 2,5
quilômetro percorrido, para a mesma categoria de carros.
Determine a quantidade de quilômetros percorridos para a
3. (G1 - cftmg 2015) Um motorista de táxi cobra, para cada qual o valor cobrado é o mesmo. Justifique sua resposta
corrida, uma taxa fixa de R$ 5,00 e mais R$ 2,00 por apresentando os cálculos realizados.
d) 3,0
quilômetro rodado. O valor total arrecadado (R) num dia é
6. (Ueg 2015) O celular de Fabiano está com 50% de
carga na bateria. Quando está completamente carregado,
e calculado por meio da função R(x)  ax  b, em que a é ele demora exatamente 20 horas para descarregar toda
o preço cobrado por quilômetro e b, a soma de todas as bateria em modo stand by, supondo-se que essa bateria se
taxas fixas recebidas no dia. Se, em um dia, o taxista descarregue de forma linear. Ao utilizar o aparelho para
função da quantidade total (x) de quilômetros percorridos
www.davidmachado.com.br
EXCELÊNCIA NO ENSINO DA MATEMÁTICA
brincar com um aplicativo a bateria passará a consumir 1%
da carga a cada 3 minutos. Quantos minutos Fabiano
poderá brincar antes que a bateria se descarregue
completamente?
a) Três horas
b) Duas horas e meia
c) Duas horas
d) Uma hora e meia
o instante em que o paciente ingere a primeira dose do
medicamento.
Álvaro é um paciente que está sendo tratado com esse
medicamento e tomou a primeira dose às 11 horas da
manhã de uma segunda-feira.
a) A que horas a concentração do medicamento na corrente
sanguínea de Álvaro atingirá 40 ppm pela primeira vez?
b) Se o médico deseja prescrever a segunda dose quando a
7. (Uepa 2015) Segundo a Organização das Nações Unidas
concentração do medicamento na corrente sanguínea de
(ONU) a população da Terra atingiu a marca de 7,2 bilhões
Álvaro atingir seu máximo valor, para que dia da semana
e horário ele deverá prescrever a segunda dose?
de habitantes em 2013, dados publicados no estudo
“Perspectivas de População Mundial”. De acordo com as
projeções de crescimento demográfico, seremos 8,1 10. (Ufrgs 2015) Considere os gráficos das funções f, g e
bilhões de habitantes em 2025 e 9,6 bilhões de habitantes h,
definidas
por
e
g(x)=x2  5x  6
f(x)=2,
em 2050. Supondo que a partir de 2025, a população
2
h(x)  x  11x  30, representadas no mesmo sistema de
mundial crescerá linearmente, a expressão que representará
o total de habitantes (H), em bilhões de pessoas, em coordenadas cartesianas.
função do número de anos (A) é:
O número de pontos distintos em que o gráfico de f
intercepta os gráficos de g e h é
a) H  0,060  A  8,1
b) H  0,036  A  7,2
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
c) H  0,060  A  9,6
d) H  0,036  A  8,1
e) H  0,060  A  7,2
8. (Fuvest 2015) A trajetória de um projétil, lançado da
beira de um penhasco sobre um terreno plano e horizontal, 11. (Uepa 2015) Leia o texto para responder à questão.
é parte de uma parábola com eixo de simetria vertical,
como ilustrado na figura abaixo. O ponto P sobre o
terreno, pé da perpendicular traçada a partir do ponto
ocupado pelo projétil, percorre 30 m desde o instante do
lançamento até o instante em que o projétil atinge o solo. A
altura máxima do projétil, de 200 m acima do terreno, é
atingida no instante em que a distância percorrida por P, a
partir do instante do lançamento, é de 10 m. Quantos
metros acima do terreno estava o projétil quando foi
lançado?
A utilização de computadores como ferramentas
auxiliares na produção de conhecimento escolar tem sido
uma realidade em muitas escolas brasileiras. O GeoGebra é
um software educacional utilizado no ensino de
Matemática (geometria dinâmica). Na ilustração acima se
tem a representação dos gráficos de duas funções reais a
valores reais, definidas por
a) 60
b) 90
c) 120
d) 150
e) 180
9. (Unifesp 2015) A concentração C, em partes por milhão
2
(ppm), de certo medicamento na corrente sanguínea após g(x)  x  x  2 e f(x)  x  5.
t horas da sua ingestão é dada pela função polinomial
C(t)  0,05t 2  2t  25. Nessa função, considera-se t  0
Fonte: http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula-53900
www.davidmachado.com.br
EXCELÊNCIA NO ENSINO DA MATEMÁTICA
Nestas condições, a soma das ordenadas dos pontos de
interseção dos gráficos que representam as duas funções
polinomiais acima ilustradas é:
a) 2
b) 5
c) 7
d) 11
e) 12
12. (Ufsm 2015) A água é essencial para a vida e está
presente na constituição de todos os alimentos. Em regiões
com escassez de água, é comum a utilização de cisternas
Desse modo, quando x assumir o maior valor inteiro
para a captação e armazenamento da água da chuva.
Ao esvaziar um tanque contendo água da chuva, a permitido, a área da região não assinalada será igual, em
metros quadrados, a
expressão
a) 84.
b) 36.
1
V(t)  
t2  3
c) 48.
43200
d) 68.
e) 64.
representa o volume (em m3 ) de água presente no tanque
no instante t (em minutos).
15. (Espcex (Aman) 2014)
Uma indústria produz
Qual é o tempo, em horas, necessário para que o tanque mensalmente x lotes de um produto. O valor mensal
seja esvaziado?
resultante da venda deste produto é V(x)  3x2  12x e o
a) 360.
custo
mensal
da
produção
é
dado
por
b) 180.
2
C(x)  5x  40x  40. Sabendo que o lucro é obtido pela
c) 120.
diferença entre o valor resultante das vendas e o custo da
d) 6.
produção, então o número de lotes mensais que essa
e) 3.
indústria deve vender para obter lucro máximo é igual a
13. (Uepb 2014) O gráfico da função f : R  R dada por a) 4 lotes.
b) 5 lotes.
f(x)  mx2  nx  p com m  0 é a parábola esboçada
c) 6 lotes.
abaixo, com vértice no ponto V. Então podemos concluir d) 7 lotes.
corretamente que:
e) 8 lotes.
16. (Ucs 2014) O lucro obtido por um distribuidor com a
venda de caixas de determinada mercadoria é dado pela
0,01 2 
6
x
x   0,6x, em que x denota
5
5

expressão L(x)  
o número de caixas vendidas.
a) m  0, n  0 e p  0
b) m  0, n  0 e p  0
c) m  0, n  0 e p  0
d) m  0, n  0 e p  0
e) m  0, n  0 e p  0
Quantas caixas o distribuidor deverá vender para que o
lucro seja máximo?
a) 60
b) 120
c) 150
d) 600
e) 1500
17. (Uece 2014) Sejam f : R  R a função definida por
14. (Uea 2014) A figura mostra um quadrado de lado igual f(x)  x2  x  1, P e Q pontos do gráfico de f tais que o
a 10 m. A região assinalada é constituída de dois
segmento de reta PQ é horizontal e tem comprimento igual
quadrados que não se intersecionam e cujos lados medem a 4 m. A medida da distância do segmento PQ ao eixo das
x metros. A área da região não assinalada pode ser obtida abscissas é
pela lei A  100  2x2 .
Observação: A escala usada nos eixos coordenados adota
o metro como unidade de comprimento.
a) 5,25 m.
www.davidmachado.com.br
EXCELÊNCIA NO ENSINO DA MATEMÁTICA
b) 5,05 m.
c) 4,95 m.
d) 4,75 m.
A figura abaixo representa o pêndulo que oscila e controla
os segundos no relógio, fazendo-o funcionar, incluindo
suas posições mais alta e mais baixa. O tic-tac é feito
através da oscilação completa do pêndulo (sai do ponto C,
18. (Enem 2014) Um professor, depois de corrigir as provas vai até o ponto E e volta ao ponto C ): esse percurso tem
de sua turma, percebeu que várias questões estavam muito um tempo total de 2 s.
difíceis. Para compensar, decidiu utilizar uma função
polinomial f, de grau menor que 3, para alterar as notas
x da prova para notas y  f(x), da seguinte maneira:
- A nota zero permanece zero.
- A nota 10 permanece 10.
- A nota 5 passa a ser 6.
A expressão da função
y  f(x) a ser utilizada pelo
professor é
1 2 7
x  x.
25
5
1 2
y   x  2x.
10
1 2 7
y
x 
x.
24
12
4
y  x  2.
5
y  x.
a) y  
b)
20. (G1 - ifsc 2015) Sobre a relação cujo domínio é o
tempo de funcionamento do relógio em segundos, e a
imagem é a altura ocupada pelo centro do círculo que
c)
compõe o pêndulo do relógio em dm, é CORRETO afirmar:
a) É uma função exponencial.
d)
b) É uma função quadrática.
e)
c) É uma função de primeiro grau.
d) É uma função periódica.
19. (Acafe 2014) O vazamento ocorrido em função de uma e) Não é uma função, pois não está definida em todo o
rachadura na estrutura da barragem de Campos Novos
conjunto domínio.
precisa ser estancado. Para consertá-la, os técnicos
verificaram que o lago da barragem precisa ser esvaziado e
estimaram que, quando da constatação da rachadura, a
capacidade C de água no lago, em milhões de metros
cúbicos, poderia ser calculada por C(t)  2t 2  12t  110,
Gabarito:
01. D
06. B
02. D
07. A
Com base no texto, analise as afirmações:
03. C
08. D
04. B
09.
l. A quantidade de água restante no lago, 4 horas depois de
05. 28Km
10. C
iniciado o vazamento, é de 30 milhões de metros cúbicos.
II. A capacidade desse lago, sabendo que estava
09. a) 21H de segunda feira
completamente cheio no momento em que começou o
b) 7H da terça feira
vazamento, é de 110 milhões de metros cúbicos.
III. Os técnicos só poderão iniciar o conserto da rachadura
quando o lago estiver vazio, isto é, 5 horas depois do
início do vazamento.
IV. Depois de 3 horas de vazamento, o lago está com 50%
de sua capacidade inicial.
onde t é o tempo em horas.
Todas as afirmações corretas estão em:
a) I - II - III
b) I - III - IV
c) III - IV
d) I - II - III - IV
TEXTO PARA A PRÓXIMA QUESTÃO:
Com base na leitura do texto abaixo, responda a(s)
questão(ões) a seguir
www.davidmachado.com.br
11. E
12. D
13. C
14. D
15. D
16. C
17. D
18. A
19. A
20. D