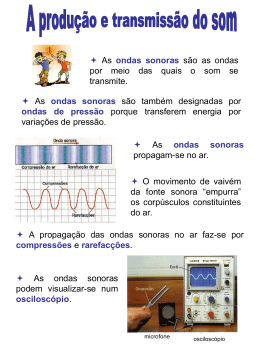
ONDAS SONORAS
Conceito:
Ondas sonoras são ondas mecânicas
longitudinais que podem se propagar em
sólidos, líquidos e gases.
A velocidade v de uma onda sonora
em um meio é dada por:
v
B

Onde:
B: módulo de elasticidade volumétrico.
ρ: massa específica do ar
Ondas Sonoras
• Equação do movimento ondulatório das ondas
sonoras
compressão
sx, t   sm coskx  t 
expansão
elemento de fluido a
oscilar
posição de
equilíbrio
px, t   pm sin kx  t 
pm  v sm
Ondas sonoras progressivas
Interferência
• A interferência de duas ondas sonoras de
mesmo comprimento de onda que passam
pelo mesmo ponto depende da diferença de
fase entre as duas nesse ponto.
• Se as ondas sonoras emitidas em fase e se
propagam aproximadamente
na mesma
direção então:
Ondas Sonoras
• Interferência
L2  L1


2

– Construtiva
L

 0, 1, 2, ...
– Destrutiva
L

 0.5, 1.5, 2.5, ...
  2
L

Intensidade e Nível Sonoro
A intensidade I de uma onda sonora em uma superfície é a taxa
média por unidade de área com a qual a energia contida na
onda atravessa a superfície ou é absorvida pela superfície.
Nível sonoro em Decibéis
Io : limiar de audição
Ondas Sonoras
• Interferência
– Batimentos ocorre quando duas ondas de
frequencias ligeramente diferentes são
detectadas simultaneamente.
s1 t   sm cos 1t
s2 t   sm cos 2t
Tempo
f bat  f1  f 2
st   2sm cos  t cos t
Ondas estacionárias em tubos
• Podem ser produzidas em tubos com as duas
extremidades abertas.
• E também com apenas uma extremidade
aberta.
Ondas Sonoras
• Ondas sonoras estacionárias (ressonância)
• Tubo aberto dos dois lados
v
fn  n
 nf1
2L
com n = 1, 2, 3, …
• Tubo aberto num dos lados
v
fn  n
 nf1
4L
com n = 1, 3, 5, …
O Efeito Doppler
É a mudança da frequência observada de uma
onda quando a fonte ou o detector está se
movendo em relação ao meio onde a onda está
se propagando.
No caso do som, a frequência
observada f’ está relacionada à
frequência f da fonte através da
equação:
v  vD
f f
v  vS
Onde:
• VD : é a velocidade do detector em relação ao
meio.
• VS : é a velocidade da fonte.
• V : é a velocidade do som no meio.
Os sinais são escolhidos para que f’ tenda a ser
maior para os movimentos de aproximação e
menor para os movimentos de afastamento.
vS
vD
vS
vD
vS
vS
vD
vD
f f
v  vD
v  vS
f f
f f
v  vD
v  vS
f f
f f
f f
v  vD
v  vS
v  vD
v  vS
Ondas Sonoras
• Efeito Doppler
v  vD
f f
v  vF
Regra: quando o movimento do detector e da fonte são de aproximação o
sinal nas suas velocidades deve resultar num aumento da frequência.
Caso se afastem, o sinal das suas velocidades deverá dar uma
diminuição da frequência
LEMBRAR
• O som é uma onda mecânica
• A luz é uma onda eletromagnética
• O som não se propaga no vácuo
• A luz pode se propagar no vácuo
• Todas as ondas eletromagnéticas são transversais
• As ondas mecânicas podem ser longitudinais, transversais ou mistas
• A luz é uma onda transversal
• O som nos fluidos é uma onda longitudinal
• A velocidade do som no ar é de 343 m/s quando t = 20º C.
• A velocidade da luz no vácuo é de 3. 105 km/s ou 3. 108 m/s
Exercícios
• Numa experiência para determinar a velocidade
do som, dois observadores colocaram-se a uma
distância de 5,0 km um do outro, munidos de um
revólver e um cronômetro. O observador em A
acionou seu cronômetro no instante em que
viu o clarão do disparo do revólver de B, tendo
registrado que o som levou 15,5 s para chegar
ao seu ouvido. Em seguida , A atirou e B registrou
o tempo de 14,5s até ouvir o estampido. Calcule
a velocidade do som e a componente da
velocidade do vento ao longo da linha AB.