Algoritmos em Grafos
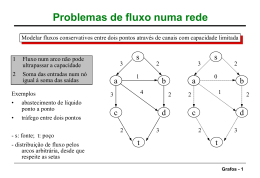
Problemas de fluxo em grafos
1º semestre/2012
Prof. André Renato
Problemas de Fluxo em Grafos
O estudo de problemas de fluxo em
grafos é de fundamental importância, pois
uma série de aplicações computacionais
podem ser modeladas através de fluxos;
 A sub-área de fluxos demanda um
conhecimento prévio de alguns conceitos
e definições para que os problemas
possam ser melhor compreendidos;

Problemas de Fluxo em Grafos
Uma rede é um digrafo D(V, E), em que
cada aresta e  E, está associada a um
número real c(e), não-negativo, chamado
capacidade da aresta e;
 D possui dois vértices especiais e
distintos s,t  V chamados de origem e
destino (fonte e sumidouro);

Problemas de Fluxo em Grafos

Um fluxo f, de s a t em D, é uma função
que associa a cada aresta e um valor real
não-negativo f(e) atendendo às seguintes
condições:
◦ 0 ≤ f(e) ≤ c(e) para cada aresta e  E;
◦
 f (u, v)   f (v, w)
uV
wV
para todo v ≠ s,t
Problemas de Fluxo em Grafos
O somatório dos fluxos das arestas
convergentes a v é igual ao somatório dos
fluxos das arestas divergentes de v;
 Este somatório é denominado valor do
fluxo em v;
 O valor do fluxo na origem é
denominado valor do fluxo na rede D e
é denotado por f(D);

Problemas de Fluxo em Grafos
Problemas de Fluxo em Grafos
Problemas de Fluxo em Grafos

Analogia:
◦ Escoamento de água em uma rede de tubos;
◦ A água é emanada de um ponto (origem) e
deve passar pela tubulação até ser recolhida
em outro ponto (destino);
◦ As junções dos tubos (demais vértices) não
produzem nem consomem água;
◦ O volume de água em cada cano deve ser tal
que a capacidade do cano não seja violada;
Problemas de Fluxo em Grafos
Naturalmente, o valor do fluxo em uma
rede pode variar de um valor igual a zero
até um certo valor máximo;
 O problema do fluxo máximo em redes
consiste em descobrir qual é este valor e
como o fluxo pode se comportar pela
rede;

Problemas de Fluxo em Grafos
Seja f um fluxo em uma rede D(V, E). Uma
aresta e  E é dita saturada quando f(e)
= c(e).
 Um vértice v  V é dito saturado se
todas as arestas convergentes a v ou
divergentes de v forem saturadas.

Problemas de Fluxo em Grafos
3(2)
d
a
3(3)
2(2)
5(4)
3(1)
s
t
c
2(2)
5(2)
b
4(3)
5(3)
e
Problemas de Fluxo em Grafos
A noção de corte em uma rede de fluxos
é de grande importância para o problema
de fluxo máximo e demais problemas de
fluxo em grafos;
 Seja S  V, um subconjunto de vértices
de V tal que s  S e t  S. Um corte (S,S),
onde S = V – S, em D é o subconjunto das
arestas de D que possuem uma
extremidade em S e outra em S.

Problemas de Fluxo em Grafos
d
a
s
t
c
b
d
a
s
e
t
c
b
e
d
a
s
t
c
b
e
Problemas de Fluxo em Grafos
É importante entender que nem sempre
os grafos são bem organizados como os
exemplos vistos;
 Desta forma, podemos ter grafos com
ciclos e arcos de mesmas extremidades,
mas sentidos diferentes;

Problemas de Fluxo em Grafos
d
a
b
c
b
b
t
e
b
s
b
b
b
Problemas de Fluxo em Grafos
É preciso diferenciar as arestas que
partem do subconjunto S daquelas que
partem do subconjunto S;
 (S,S)+ = {(u,v) | u  S e v  S};
 (S,S)- = {(u,v) | u  S e v  S};

Problemas de Fluxo em Grafos
A capacidade c(S,S) de um corte (S,S) é o
somatório das capacidades das arestas
(S,S)+;
 Um corte mínimo é aquele que possui
capacidade mínima;

Problemas de Fluxo em Grafos

Seja f um fluxo e (S,S) um corte em D.
Então f(S,S) é o fluxo do corte (S,S),
definido como:
f (S , S ) 
 f (e)   f (e)
e( s , s ) 
e( s , s ) 
Problemas de Fluxo em Grafos
Seja f um fluxo em uma rede D. O
objetivo do problema de fluxo máximo é
aumentar f, se possível.
 Cada aresta e pode receber um fluxo
adicional ≤ c(e) – f(e);
 Talvez este fluxo adicional aumente o
valor do fluxo em D;

Problemas de Fluxo em Grafos
Uma aresta e tal que c(e) – f(e) > 0
chama-se aresta direta;
 Uma aresta e só pode receber
decremento positivo de fluxo se e
somente f(e) > 0; estas são chamadas de
arestas contrárias;
 Uma aresta pode ser somente direta,
somente contrária ou direta e contrária;

Problemas de Fluxo em Grafos
3(2)
d
a
3(3)
2(2)
5(4)
3(0)
s
t
c
2(0)
5(2)
b
4(3)
5(3)
e
Problemas de Fluxo em Grafos

Dados um fluxo f e uma rede D(V,E), a
rede residual D´(f) é aquela cujo conjunto
de vértices coincide com os de V e cujas
arestas são obtidas assim:
◦ Se uma aresta (u,v) é direta em D, então (u,v)
é também aresta direta de D´ e sua
capacidade é c(u,v) – f(u,v);
◦ Se uma aresta (u,v) é contrária em D, então
(v,u) é também aresta contrária de D´ e sua
capacidade c(v,u) = f(u,v);
Problemas de Fluxo em Grafos
Problemas de Fluxo em Grafos
a
4(2)
s
2(1)
3(2)
1(1)
2(2)
b
t
3(0)
4(3)
3(1)
d
c
3(1)
5(2)
Problemas de Fluxo em Grafos
Em outras palavras, as capacidades das
arestas na rede residual representam as
possíveis variações de fluxo que as arestas
de D podem sofrer, com a direção
indicando a variação positiva ou negativa;
 Um caminho de s a t na rede residual
D´(f) é chamado de aumentante para o
fluxo f.

Problemas de Fluxo em Grafos
Problemas de Fluxo em Grafos
Se todo caminho entre s e t em uma rede
D passar por uma aresta e, o fluxo
máximo desta rede não pode ser maior
do que c(e) – gargalo;
 De forma mais geral, o valor de um fluxo
f em D não pode ultrapassar o valor de
qualquer corte (S,S);

Problemas de Fluxo em Grafos
f(D) = f(S,S) =
=
≤
 f (e)   f (e)
e( s , s )

 f (e)
e( s , s )

e( s , s )

= c(S,S)
Logo, f(D) ≤ c(S,S).
≤
Problemas de Fluxo em Grafos

Teorema do fluxo máximo – corte
mínimo:
◦ O valor do fluxo máximo de uma rede D é
igual à capacidade do corte mínimo de D.
Problemas de Fluxo em Grafos

Algoritmos para Fluxo máximo:
◦ Dados de entrada:
 D(V, E)
 Cada aresta e tem capacidade c(e), inteira e positiva
 Origem s e destino v de V
◦ Saída:
 F: valor do fluxo na rede
 f(e): valor do fluxo em cada aresta e
Problemas de Fluxo em Grafos

Algoritmo 1:
◦
◦
◦
◦
F = 0;
Para cada aresta e, f(e) = 0;
Construir a rede residual D’(f)
Enquanto existir caminho de s a t em D’:
 F’ = min{ c’(vj,vj+1) | 1≤ j < k }
 Para j de 1 até k-1
 Se (vj,vj+1) é aresta direta entao
 f(vj,vj+1) = f(vj,vj+1) + F’
 Senão f(vj+1,vj) = f(vj+1,vj) – F’
 F = F + F’
 Construir rede residual D’(f)
Problemas de Fluxo em Grafos
a
4
s
2
3
1
2
b
t
3
4
3
d
c
3
5
Problemas de Fluxo em Grafos

Qual o problema que pode existir neste
algoritmo?
Problemas de Fluxo em Grafos

Algoritmo 2:
◦
◦
◦
◦
F = 0;
Para cada aresta e, f(e) = 0;
Construir a rede residual D’(f)
Enquanto existir caminho de s a t em D’:
 Escolher o menor caminho (via busca em largura)
 F’ = min{ c’(vj,vj+1) | 1≤ j < k }
 Para j de 1 até k-1
 Se (vj,vj+1) é aresta direta entao
 f(vj,vj+1) = f(vj,vj+1) + F’
 Senão f(vj+1,vj) = f(vj+1,vj) – F’
 F = F + F’
 Construir rede residual D’(f)
Problemas de Fluxo em Grafos
a
4
s
2
3
1
2
b
t
3
4
3
d
c
3
5
Problemas de Fluxo em Grafos
Um segundo problema muito comum de
fluxo em redes consiste em descobrir o
fluxo de menor custo (custo mínimo);
 Neste caso, não estamos mais
preocupados em encontrar o fluxo
máximo;

Problemas de Fluxo em Grafos
O vértice de destino t vai possuir agora
uma demanda positiva de um fluxo;
 Essa demanda será denotada por B;
 O vértice s terá uma oferta de fluxo,
também com valor B;
 Os demais vértices não terão oferta nem
demanda;

Problemas de Fluxo em Grafos
O objetivo está em fazer um fluxo de B
unidades atravessar o grafo de s a t,
passando pelas arestas (com capacidade
positiva);
 Cada aresta vai possuir também um custo
de utilização caso passe fluxo por ela.
 Estamos interessados em escolher as
arestas que ofereçam os menores custos;

Problemas de Fluxo em Grafos
Demanda = 7
(custo, capacidade)
Soluções?????
a
(3,4)
s
(4,2)
(2,3)
(1,1)
(5,2)
b
t
(1,3)
(5,4)
(3,3)
d
c
(2,3)
(2,5)
Problemas de Fluxo em Grafos

Aplicações
◦ Uma empresa possui p fábricas com produção
conhecida e q depósitos com demandas
conhecidas. Deseja-se estabelecer um fluxo
que atenda às demandas, de forma que o
custo de transporte dos produtos das fábricas
para os depósitos seja o menor possível.
Problemas de Fluxo em Grafos

Aplicações
◦ Uma generalização deste problema envolve a
fabricação de produtos distintos, com
produções e demandas também distintos.
◦ Neste caso, pode-se utilizar uma estratégia
muito interessante de se criar camadas de nós
intermediários para tratar os modelos
diferentes de forma distinta;
Problemas de Fluxo em Grafos
Problemas de Fluxo em Grafos

Algoritmo de ciclos negativos
(cancelamento de ciclos):
◦ A ideia é encontrar um fluxo inicial factível;
◦ Depois, monta-se a rede residual;
◦ Enquanto houver ciclos de custo negativo,
aumenta-se o fluxo através do ciclo;
◦ O algoritmo termina quando não houver mais
ciclos;
Problemas de Fluxo em Grafos

Algoritmo:
◦ Estabelecer um fluxo F através do algoritmo
de fluxo máximo;
◦ Montar a rede residual W;
◦ Enquanto a rede W tem ciclo negativo:
 Determinar x = min{rij, (i,j)  W};
 Aumentar o fluxo F em x unidades;
 Montar a rede residual W;
◦ Fim enquanto;
Problemas de Fluxo em Grafos

Como montar a rede residual em um
grafo com capacidade, custo e fluxo para
cada aresta?
(2,1)
(2,2)
(2,3)
1
(2,4)
1
0
1 (2,5)
(3,3)
3
(-2,1)
(1,4)
(1,3)
(-2,1)
(1,4) (-2,1) (2,4)
(-1,3)
(-3,3)
3
(custo, capacidade)
fluxo
(custo, residual)
Problemas de Fluxo em Grafos
(2,5)
a
(2,4)
(3,7)
s
f
(1,5)
(2,5) (2,6)
c
b
(3,1)
(1,2)
(4,5)
e
(1,7)
(2,5)
(2,4)
(3,5)
t
(3,3)
d
Problemas de Fluxo em Grafos

Problema de múltiplos fluxos:
◦ É uma generalização do problema de luxo de
custo mínimo;
◦ Ao invés de um único tipo de fluxo (produtos,
mercadorias etc) temos vários fluxos distintos
sendo produzidos e consumidos;
◦ Ex: por determinadas redes, passam tráfegos
de tipos diferentes
 Dados
 Voz
 Audio ou video on-line
Problemas de Fluxo em Grafos
Se os fluxos não apresentam qualquer
tipo de interação entre si, o problema
pode ser tratado separadamente como
diversos problemas de fluxo;
 Entretanto, se os fluxos compartilham
determinadas características, será preciso
tratar o problema como um todo;

Problemas de Fluxo em Grafos
Fluxo 1
i
j
Fluxo 2
Fluxo 3
xij1
xij2
xij3
uij
Problemas de Fluxo em Grafos

Algumas variações:
◦ Homogeneidade: cada unidade de fluxo que
passa por uma aresta consume uma unidade
de capacidade da aresta;
◦ Custos crescentes: em alguns modelos o
custo é definido como uma função não-linear
(função degrau);
◦ Integralidade: na maioria dos modelos, o fluxo
pode ser transferido em unidades inteiras
(não-fracionárias);