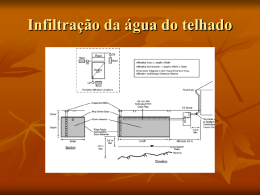
Processos Hidrológicos
CST 318 / SER 456
Tema 6 – Água no Solo
ANO 2015
Camilo Daleles Rennó
Laura De Simone Borma
http://www.dpi.inpe.br/~camilo/prochidr/
Fluxo de água no solo
A água se desloca em resposta a uma diferença de potencial, isto é, sempre que
houver diferença de potencial entre dois pontos de um sistema, a água
estará se movendo do ponto onde o potencial total é maior para o ponto onde
ele é menor.
A
A
A
B
B
B
𝜓𝐴 > 𝜓𝐵
𝜓𝐴 < 𝜓𝐵
𝜓𝐴 = 𝜓𝐵
Mas há como medir a velocidade deste deslocamento?
Fluxo de água no meio saturado
Darcy (em 1856) estudou o escoamento da água em meios porosos saturados (colunas de
areia), verificando que a vazão de saída (𝑄, m3h-1) era diretamente proporcional à
perda de carga (Δℎ, m) e à seção transversal da coluna da amostra (𝐴, m2) e
inversamente proporcional ao comprimento desta mesma coluna (𝐿, m).
𝑄 = 𝐾𝑠 𝐴
𝐿
Δℎ
ℎ1
𝐴
𝑄
Nível de Referência
ℎ2
Δℎ
𝐿
𝐾𝑠 é condutividade hidráulica
num meio saturado (mh-1)
Δℎ
𝑞 = 𝐾𝑠
𝐿
𝑞
𝑣=
𝜙
velocidade do
fluxo laminar
(mh-1 = m3m-2h-1)
velocidade de
percolação
(considera apenas os poros)
Lei de Darcy
A lei de Darcy pode ser aplicada para o cálculo do fluxo de água em meios saturados
considerando qualquer direção.
Em sua forma mais geral, considerando qualquer ponto da zona saturada do solo, a
lei de Darcy pode ser reescrita como:
𝑞 = −𝐾𝑠
𝜕𝜓𝑡
𝜕𝑑
Sendo 𝜕𝜓𝑡 /𝜕𝑑 a variação do potencial total 𝜓𝑡 ao longo da direção d.
Em estudos tridimensionais, este fluxo pode ser decomposto segundo 3 eixos:
𝑞𝑥 = −𝐾𝑠
𝜕𝜓𝑡
𝜕𝑥
𝑞𝑦 = −𝐾𝑠
𝜕𝜓𝑡
𝜕𝑦
𝑞𝑧 = −𝐾𝑠
𝜕𝜓𝑡
𝜕𝑧
(meio isotrópico)
Considerando um meio saturado, o potencial total é formado por dois componentes:
o potencial gravitacional, que é determinado pela altura relativa ao plano de
referência no qual uma partícula de água se encontra; e o potencial de pressão,
que é determinado pela altura da coluna de água acima desta partícula.
Condutividade Hidráulica (meio saturado)
A condutividade hidráulica 𝐾𝑠 expressa a facilidade com que um fluido é
transportado através de um meio poroso e combina as propriedades do
fluido e do meio:
𝐾𝑠 =
𝑘𝜌𝑔
𝜇
Sendo 𝑘 a permeabilidade intrínseca (m2) que depende apenas do material
poroso (granulometria e disposição estrutural), 𝜌 é a densidade do fluido
(kg m-3), 𝑔 é a aceleração gravitacional (m s-2) e 𝜇 é a viscosidade dinâmica
do fluido (N s m-2). Neste caso, Ks é dado em m s-1.
Condutividade Hidráulica (meio saturado)
A condutividade hidráulica (meio saturado) é afetada pela estrutura e textura do
solo, sendo maior em solos porosos (poros grandes), fraturados e bem
estruturados (formação de agregados). Ou seja, não depende apenas da
quantidade de poros, mas também do tamanho e da geometria desses poros
(tortuosidade) por onde o fluido irá ser conduzido.
Por isso, em geral, solos arenosos apresentam condutividade hidráulica maior que
solos argilosos quando saturados.
Fluxo de água no meio não saturado
O movimento da água no solo no meio saturado é controlado por potenciais de pressão
sempre positivos. Já, num meio não saturado, o potencial de pressão é negativo
(potencial matricial). Neste caso, a água tende a se deslocar dos poros onde a
película tem maior espessura em direção aos poros cuja película é mais fina.
Quando o solo não está saturado, alguns poros estão preenchidos também pelo ar, e a
capacidade de transmitir água desse poro diminui. A medida que a quantidade de
água no solo se reduz, os poros maiores começam a se esvaziar, fazendo com que a
água só possa fluir pelos poros menores.
Fluxo de água no meio não saturado
Na saturação, os poros maiores conduzem a maior parte da água. Por isso, solos de
textura grossa apresentam maior condutividade hidráulica na saturação. O
contrário ocorre no fluxo não saturado: os solos de textura fina tem maior
quantidade de poros menores, os quais são capazes de reter e conduzir mais água
que os solos de textura grossa quando submetidos à mesma tensão.
𝐾𝑠(𝑎𝑟𝑒𝑖𝑎)
𝐾𝑠(𝑎𝑟𝑔𝑖𝑙𝑎)
𝐾
argila
areia
𝜃
𝐾𝑠(𝑎𝑟𝑒𝑖𝑎) > 𝐾𝑠(𝑎𝑟𝑔𝑖𝑙𝑎)
𝐾(𝑎𝑟𝑒𝑖𝑎) < 𝐾(𝑎𝑟𝑔𝑖𝑙𝑎)
𝜃𝑠
Condutividade Hidráulica
Em meio não saturado, a lei de Darcy ainda continua válida, mas a condutividade
hidráulica 𝐾 diminui rapidamente com a diminuição da umidade. A
condutividade hidráulica é máxima em condições de saturação (𝐾𝑠 ).
Campbell (1974) formulou uma relação bastante prática para o cálculo da
condutividade hidráulica:
𝐾 𝜃 = 𝐾𝑠
𝜃
𝜃𝑠
2𝑏+3
(1978) determinaram valores do coeficiente 𝑏
para solos com diferentes texturas, chegando a
uma relação muito forte entre o coeficiente 𝑏 e o
Coeficiente b
onde 𝑏 é um coeficiente empírico. Clapp e Hornberger
teor de argila do solo.
Campbell, G.S. A simple method for determining unsaturated conductivity from moisture retention data. Soil Sci., 117(6):311-314, 1974.
Clapp, R.B.; Hornberger, G.M. Empirical equations for some soil hydraulic properties. Water Resour. Res., 14(4):601-604, 1978.
teor de argila
Condutividade Hidráulica
Modelo de Mualem (1976)
𝑆𝑒
1/2
𝐾 𝑆𝑒 = 𝐾𝑠 𝑆𝑒
0
1
𝑑𝑆
𝜓(𝑆)
1
0
2
1
𝑑𝑆
𝜓(𝑆)
𝑆𝑒 =
𝜃 − 𝜃𝑟
𝜃𝑠 − 𝜃𝑟
Substituindo em Brooks-Corey:
𝜓𝑏
𝑆𝑒 =
𝜓𝑚
𝜓𝑏
𝜆
𝐾 𝑆𝑒 =
1
2+ +2/𝜆
𝐾𝑠 𝑆𝑒 2
𝐾 𝑆𝑒 =
1/2
𝐾𝑠 𝑆𝑒
𝐾/𝐾𝑠
Substituindo em van Genuchten:
𝑆𝑒 =
1
1 + 𝛼 𝜓𝑚
1
𝑛 1−𝑛
1− 1−
2
1/𝑚 𝑚
𝑆𝑒
𝑚 = 1 − 1/𝑛
Mualem Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res.,12(3):513–522, 1976.
|𝜓𝑚 | (𝑘𝑃𝑎)
Fluxo de água no meio não saturado
A lei de Darcy (que considerava condições de fluxo saturado) foi generalizada por
Richards para as condições não saturadas, levando-se em conta que a
condutividade hidráulica 𝐾 é função do potencial matricial do solo, ou seja 𝐾 𝜓𝑚 .
Considerando-se apenas o fluxo unidimensional vertical tem-se, pela lei de Darcy,
que:
𝑞𝑧 = −𝐾(𝜓𝑚 )
𝜕(𝜓𝑚 + 𝜓𝑔 )
𝜕𝜓𝑡
𝜕𝜓𝑚
= −𝐾(𝜓𝑚 )
= −𝐾(𝜓𝑚 )
+1
𝜕𝑧
𝜕𝑧
𝜕𝑧
𝜕𝜓𝑚 𝜕𝜃
𝜕𝜓𝑚
=
−
𝐾(𝜓
)
+ 𝐾(𝜓𝑚 )
= − 𝐾(𝜓𝑚 )
+ 𝐾(𝜓𝑚 )
𝑚
𝜕𝜃 𝜕𝑧
𝜕𝑧
𝜕𝜃
= − 𝐷(𝜃)
+ 𝐾(𝜃)
𝜕𝑧
𝐷(𝜃) = 𝐾(𝜓𝑚 )
𝜕𝜓𝑚
𝜕𝜃
(Difusividade hidráulica)
Fluxo de água no meio não saturado
Para se entender como a umidade do solo varia ao longo do tempo, deve-se
considerar a equação de continuidade:
𝑞𝑧
𝜕𝜃
𝜕𝑞𝑧
=−
𝜕𝑡
𝜕𝑧
𝜕𝑧
𝑞𝑧 +
𝜕𝑞𝑧
𝜕𝑧
Combinando-se a equação de continuidade com a de Darcy, tem-se as duas
formas da equação de Richards:
𝜕𝜃
𝜕
𝜕𝜃
=
𝐷(𝜃)
+ 𝐾(𝜃)
𝜕𝑡 𝜕𝑧
𝜕𝑧
𝐶(𝜓𝑚 )
𝜕𝜓𝑚
𝜕
𝜕𝜓𝑚
=
𝐾(𝜓𝑚 )
+1
𝜕𝑡
𝜕𝑧
𝜕𝑧
𝐶(𝜓𝑚 ) =
𝜕𝜃
(Capacidade específica)
𝜕𝜓𝑚
derivada da curva de retenção
Considerações importantes
O tamanho dos poros é um dos fatores que mais afetam o movimento da água no solo.
Quando considerado um solo em condições de saturação, poros maiores (areias)
conduzem mais água que poros menores (argilas), ou seja, 𝐾𝑠
𝑎𝑟𝑒𝑖𝑎
> 𝐾𝑠
𝑎𝑟𝑔𝑖𝑙𝑎
Considerações importantes
O tamanho dos poros é um dos fatores que mais afetam o movimento da água no solo.
Quando considerado um solo em condições de saturação, poros maiores (areias)
conduzem mais água que poros menores (argilas), ou seja, 𝐾𝑠
𝑎𝑟𝑒𝑖𝑎
> 𝐾𝑠
𝑎𝑟𝑔𝑖𝑙𝑎
Em condições não saturadas, os caminhos que a água deve percorrer se tornam tortuosos.
Quanto mais tortuosos, menor a condutividade hidráulica. Nestas condições, os solos
arenosos têm menor capacidade de conduzir água que os solos argilosos, ou seja,
𝐾(𝑎𝑟𝑒𝑖𝑎) < 𝐾
𝑎𝑟𝑔𝑖𝑙𝑎
.
Considerações importantes
Em geral, solos arenosos têm poros maiores que os solos argilosos, mas têm porosidade
(espaço poroso) menor e por isso armazenam menos água por unidade de volume que
solos argilosos.
𝜃𝑠 (𝑎𝑟𝑒𝑖𝑎) < 𝜃𝑠 (𝑎𝑟𝑔𝑖𝑙𝑎)
Considerações importantes
Em geral, solos arenosos têm poros maiores que os solos argilosos, mas têm porosidade
(espaço poroso) menor e por isso armazenam menos água por unidade de volume que
solos argilosos.
𝜃𝑠 (𝑎𝑟𝑒𝑖𝑎) < 𝜃𝑠 (𝑎𝑟𝑔𝑖𝑙𝑎)
Mudanças no tamanho e na distribuição de poros afetam o movimento de água no solo:
compactação, canais de raízes deixados por raízes mortas, túneis de minhocas e de
outros animais, fendas, etc.
Considerações importantes
Em geral, solos arenosos têm poros maiores que os solos argilosos, mas têm porosidade
(espaço poroso) menor e por isso armazenam menos água por unidade de volume que
solos argilosos.
𝜃𝑠 (𝑎𝑟𝑒𝑖𝑎) < 𝜃𝑠 (𝑎𝑟𝑔𝑖𝑙𝑎)
Mudanças no tamanho e na distribuição de poros afetam o movimento de água no solo:
compactação, canais de raízes deixados por raízes mortas, túneis de minhocas e de
outros animais, fendas, etc.
Em alguns casos, uma camada do solo pode ter condutância hidráulica inferior que camadas
superiores, o que provocará o retardamento da percolação, podendo inclusive formar
uma zona saturada suspensa intermitente.
P
P
Horizonte 1
Horizonte 2
Limitações das Equações Clássicas
•
As equações de Richards envolvem cálculos diferenciais altamente não-
lineares, o que dificulta a solução numérica (processos iterativos sem garantia
total de convergência).
𝑞𝑧
𝜕𝑧1
𝑞𝑧 +
𝜕𝑞𝑧1
= 𝑞𝑧1
𝜕𝑧1
𝜕𝑧2
𝑞𝑧1 +
𝜕𝑞𝑧2
𝜕𝑧2
Limitações das Equações Clássicas
•
As equações de Richards envolvem cálculos diferenciais altamente nãolineares, o que dificulta a solução numérica (processos iterativos sem garantia
total de convergência).
•
Grandes restrições quanto à representatividade espacial de amostras.
•
A existência de fluxos preferenciais no solo (macroporos e canais) não
obedecem a lei de Darcy.
•
Os perfis do solo são, em geral, anisotrópicos causando uma irregularidade
nas frentes de umedecimento de difícil modelagem.
Exemplo
Dois tensiômetros (A e B) foram instalados
na zona não saturada de um solo franco-
arenoso. A distância entre a cápsula
porosa (bulbo) e medidor de pressão é de
61 cm. O tensiômetro A mede a tensão
61 cm
matricial a 20 cm e o B a 50 cm. Qual o
sentido e velocidade do fluxo laminar
vertical 𝑞𝑧 entre os pontos A e B, sabendo
20 cm
61 cm
que pressão medida pelos tensiômetros A e
B foram -151 cm e -117 cm,
respectivamente? Calcule também a
50 cm
A
umidade volumétrica 𝜃 nos pontos.
B
Exemplo
Primeiramente, calcula-se o potencial matricial no bulbo somando-se 61 cm de
cada leitura. Isto porque a leitura feita no sensor considera não apenas o
potencial matricial no bulbo, mas também o peso da coluna de água acima do
bulbo, assim:
𝜓𝑚(𝐴) = −151 + 61 = −90 cm
𝜓𝑚(𝐵) = −117 + 61 = −56 cm
Como os pontos estão em profundidades diferentes, é
necessário também considerar o potencial gravitacional
em cada ponto. Para tanto, é necessário adotar um nível
de referência. Considerando como referência a
61 cm
superfície, o potencial gravitacional nos pontos A e B é:
20 cm
61 cm
𝜓𝑔(𝐴) = −zA = −20 cm
𝜓𝑔(𝐵) = −zB = −50 cm
50 cm
A
B
B
𝜓𝑚 (cm)
-90
-56
𝜓𝑔 (cm)
-20
-50
𝜓𝑡 (cm)
-110
-106
0,1333
𝜕𝜓𝑡 /𝜕𝑧
𝑆𝑒
0,6618
0,7918
𝜃 (cm3/cm3)
0,3137
0,3672
𝐾 (cm/h)
0,1039
0,4202
𝑞𝑧 (cm/h)
𝜕𝜓𝑡
𝑞𝑧 = −𝐾(𝜓𝑚 )
𝜕𝑧
𝜓𝑡(𝐴) < 𝜓𝑡(𝐵)
Rawls et al. (1982)
A
-0,0349
𝜃 − 𝜃𝑟
𝑆𝑒 =
𝜃𝑠 − 𝜃𝑟
Usando a equação BC
𝜓𝑏
𝑆𝑒 =
𝜓𝑚
𝜆
−30,20
=
−90
0,378
= 0,6618
(fluxo ascendente)
1
2+ +2/𝜆
𝐾 𝑆𝑒 = 𝐾𝑠 𝑆𝑒 2
𝜃 = 𝜃𝑠 − 𝜃𝑟 𝑆𝑒 + 𝜃𝑟
= 2,59 0,6618
61 cm
2,5+2/0,378
= 0,1039
20 cm
61 cm
50 cm
= 0,453 − 0,041 0,6618 + 0,041 = 0,3137
𝑞𝑧 = −
0,1039 + 0,4202
0,1333 = −0,0349
2
A
B
Rawls, W.J.; Brakensiek, D.L.; Saxton, K.E. (1982). Estimation of soil water properties. Transaction of the ASAE, 25(5):1316-1320.
Exemplo
Infiltração e Percolação
chuva
escoamento
superficial
infiltração
Zona de
Aeração
(não saturada)
Zona de
Saturação
a – condição inicial
b, c – infiltração
d, e - percolação
lençol freático
rocha
percolação
lençol freático
Baseado em Hewlett (1982)
rocha
Infiltração é o processo de passagem da água pela superfície do solo.
Percolação é o avanço descendente da água na zona não saturada.
Perfil de umidade durante a infiltração
umidade
𝜃𝑠
zona de saturação
profundidade do solo
Zona de Aeração
(não saturada)
A umidade varia com a profundidade a
zona de
transmissão
zona de
umedecimento
frente de
umedecimento
medida que a água vai preenchendo os
espaços porosos do solo.
A medida que o tempo passa, aumenta-se a
zona de transmissão e portanto a
profundidade da área de umedecimento.
Frente de Umedecimento
Frente
uniforme
Frente
heterogênea
Solos
permeáveis
bem agregados
Solos
heterogêneos
Frente lateral
em macroporos
com pouca
interação
Frente lateral
em macroporos
com alta
interação
Solo com
macroporos
com pouca
permeabilidade
Solos com
macroporos
com muita
permeabilidade
Etapas da Infiltração
Considerando-se uma condição inicial não saturada, a infiltração é função dos
potenciais matricial e gravitacional.
Inicialmente, o potencial matricial domina o processo succionando a água para
dentro do perfil. Com a redistribuição da água ao longo do perfil do solo, a
umidade tende a aumentar e este potencial perde progressivamente sua
importância.
Próximo à saturação, o potencial gravitacional torna-se predominante.
Caso a intensidade de chuva ultrapasse a capacidade de infiltração, ocorre o
escoamento superficial por excesso de precipitação.
O empoçamento da água cria uma lâmina de água à superfície que passa a
exercer uma pressão adicional (potencial de carga) importante no processo
de infiltração.
Fatores que afetam a Infiltração
Textura e estrutura do solo: porosidade, densidade e compactação do solo
maior quantidade de poros grandes  maior infiltração
maior compactação  maior densidade  menor infiltração
Condição antecedente de umidade do solo
mais úmido  menor infiltração
Atividade biológica e matéria orgânica
mais matéria orgânica  melhor estruturado é o solo  maior infiltração
Presença de cobertura morta e vegetação
menor cobertura  maior desagregação das partículas  menor infiltração
Outros: hidrofobia do solo, congelamento superficial
Taxa e Capacidade de Infiltração
Taxa de infiltração: é a taxa na qual a água penetra no solo, expressa em termos
de lâmina, ou seja, mm/h (correspondente ao volume de água que penetra no
perfil do solo expresso por unidade de área, por unidade de tempo). Esta
taxa é limitada pela capacidade de infiltração do solo e pela intensidade da
chuva.
Capacidade de infiltração: é a taxa máxima na qual a água consegue se infiltrar
no solo sob condições ideais.
𝐾𝑠
Infiltração sem encharcamento
umidade
Ф=θs
taxa
profundidade do solo
θ0
𝐾𝑠
𝑝
0
tempo
Ocorre quando a intensidade da precipitação (𝑝) é menor do que a condutividade
hidráulica considerando uma condição de saturação (𝐾𝑠 ).
Infiltração sem encharcamento
umidade
θ0
t1
θf
t2
Ф=θs
taxa
profundidade do solo
t3
𝐾𝑠
𝑝
0
𝑖
tempo
Ocorre quando a intensidade da precipitação (𝑝) é menor do que a condutividade
hidráulica considerando uma condição de saturação (𝐾𝑠 ).
Infiltração sem encharcamento
umidade
t1
θf
t2
t4
t5
Ф=θs
t3
taxa
profundidade do solo
θ0
𝐾𝑠
𝑖=𝑝
𝑝
0
tempo
Ocorre quando a intensidade da precipitação (𝑝) é menor do que a condutividade
hidráulica considerando uma condição de saturação (𝐾𝑠 ).
A umidade final não atinge a condição de saturação (𝜃𝑓 < 𝜃𝑠 ) e a infiltração (i)
será igual a precipitação.
Infiltração com encharcamento (Horton)
umidade
Ф=θs
𝑝
taxa
profundidade do solo
θ0
𝐾𝑠
0
tempo
Ocorre quando a intensidade da precipitação (𝑝) é maior do que a condutividade
hidráulica considerando uma condição de saturação (𝐾𝑠 ), mas inferior a
capacidade (taxa máxima) de infiltração.
Infiltração com encharcamento (Horton)
umidade
t1
t2
t3=tp
Ф=θs
𝑝
𝑖
taxa
profundidade do solo
θ0
𝐾𝑠
0
tp
tempo
Ocorre quando a intensidade da precipitação (𝑝) é maior do que a condutividade
hidráulica considerando uma condição de saturação (𝐾𝑠 ), mas inferior a
capacidade (taxa máxima) de infiltração.
A umidade final atinge a condição de saturação no tempo tp e a infiltração (i)
começa a decair.
Infiltração com encharcamento (Horton)
umidade
t1
t2
t3=tp
Ф=θs
𝑝
t4
t5
taxa
profundidade do solo
θ0
t6
𝑖
𝐾𝑠
0
tp
tempo
Ocorre quando a intensidade da precipitação (𝑝) é maior do que a condutividade
hidráulica considerando uma condição de saturação (𝐾𝑠 ), mas inferior a
capacidade (taxa máxima) de infiltração.
A umidade final atinge a condição de saturação no tempo tp e a infiltração (i)
começa a decair.
A taxa de infiltração decai até atingir valores próximos a 𝐾𝑠
Infiltração x Escoamento Superficial
umidade
t1
t2
profundidade do solo
θ0
Ф=θs
t3
t4
Considerando um solo cuja superfície está seca
(condição inicial – t0) e uma chuva cuja
intensidade é constante p:
O potencial matricial (sucção) é muito
negativo na superfície gerando gradientes
de potencial total muito baixos
t5
A capacidade de infiltração é alta
Toda a precipitação transforma-se em
infiltração
precipitação
𝑝
taxa
infiltração
𝐾𝑠
escoamento
superficial
0
t4 = tp
tempo
A medida que a água se distribui ao longo do
perfil:
O potencial matricial torna-se menos negativo
e a taxa de infiltração diminui
Há saturação da camada superficial
A precipitação em excesso origina
escoamento superficial (Horton)
Infiltração x Escoamento Superficial
umidade
θ0
t1
t4 Ф=θs
t2
profundidade do solo
t3
Com o lençol freático próximo a superfície:
t4
t3
t  t2
Um pequeno volume de água infiltra e
rapidamente o solo se torna
completamente saturado (elevação do
lençol freático)
Com a saturação, a infiltração é
interrompida
taxa
Toda a precipitação transforma-se em
escoamento direto (Dunne)
precipitação
infiltração
escoamento
superficial
𝐾𝑠
Está relacionado com o conceito de área de
contribuição variável (áreas de escoamento
direto)
𝑝
0
Ocorre geralmente nas áreas de várzea e áreas
com topografia convergente (“grotas”)
t5 = tp
tempo
Modelos de Infiltração
A estimativa da infiltração é feita através de equações baseadas em modelos
físicos ou em relações empíricas.
Em geral baseiam–se em algumas das propriedades do solo e permitem a
estimativa de infiltração a partir de poucas observações.
Green – Ampt (1911)
Equação de infiltração desenvolvida a partir de um modelo aproximado que
se baseia na lei de Darcy
Foi desenvolvido quando há o empoçamento da água em solos profundos e
homogêneos com conteúdo inicial de água com distribuição uniforme.
Horton (1940) e Philip (1957)
Equações de infiltração baseadas em soluções aproximadas da equação de
Richards
Equação de Horton (1940)
Este modelo é aplicável somente quando a intensidade de precipitação (𝑝) é
superior a condutividade hidráulica em condição de saturação (𝐾𝑠 )
Foi deduzido a partir da equação de Richards considerando constantes os valores
de difusividade hidráulica e a condutividade hidráulica, chegando-se a seguinte
relação:
𝑓(𝑡) é a taxa de infiltração no tempo 𝑡
𝑓(𝑡) = 𝑓𝑐 + 𝑓0 − 𝑓𝑐 𝑒 −𝑘𝑡
𝑓0 é a capacidade de infiltração inicial
𝑓𝑐 é a capacidade de infiltração final (~𝐾𝑠 )
𝑘 é a constante de recessão
𝑡𝑝 é o tempo para o início do empoçamento
taxa
𝑝
𝑖
𝐹𝑝 = 𝑝 𝑡𝑝
𝐾𝑠
0
tp
𝐹𝑝 é a infiltração acumulada até o empoçamento
tempo
𝐹(𝑡) é a infiltração acumulada no tempo 𝑡 após o empoçamento
𝑡
𝐹(𝑡) =
𝑓 𝑡 𝑑𝑡 = 𝑓𝑐 𝑡 − 𝑡𝑝 +
𝑡𝑝
𝑓0 − 𝑓𝑐
1 − 𝑒 −𝑘
𝑘
𝑡−𝑡𝑝
Particionamento de Fluxo (Horton)
Suponha que o processo de
empoçamento inicia-se no
tempo 𝑡𝑝
𝑓(𝑡) = 𝑓𝑐 + 𝑓0 − 𝑓𝑐 𝑒 −𝑘𝑡
taxa de infiltração
taxa de precipitação
A lâmina de água infiltrada até
este momento corresponde a
área cinza (𝐹𝑝 )
Como esta área é menor do que a
área sobre a curva de
capacidade de infiltração
(𝑓), esta função não pode ser
diretamente empregada
𝐹𝑝
𝑡𝑝
tempo
Particionamento de Fluxo (Horton)
𝑡−𝑡0
taxa de infiltração
taxa de precipitação
𝑓(𝑡 − 𝑡0 ) = 𝑓𝑐 + 𝑓0 − 𝑓𝑐 𝑒 −𝑘
𝑡0
𝑡𝑝
tempo
Suponha que o processo de
empoçamento inicia-se no
tempo 𝑡𝑝
A lâmina de água infiltrada até
este momento corresponde a
área cinza (𝐹𝑝 )
Como esta área é menor do que a
área sobre a curva de
capacidade de infiltração
(𝑓), esta função não pode ser
diretamente empregada
Para contornar este problema, a
curva 𝑓(𝑡) é deslocada no
tempo de maneira a que a
infiltração acumulada entre
𝑡0 e 𝑡𝑝 (área hachurada) seja
igual a 𝐹𝑝 .
O escoamento está representado
pela área entre 𝑓(𝑡 − 𝑡0 ) e a
precipitação (área azul).
Medição da Infiltração
• Infiltrômetros
Simples
Duplo Anel
• Infiltrômetro de carga constante
• Infiltrômetros de tensão
• Infiltrômetros em parcelas de escoamento