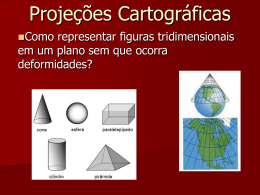
Projeções Cartográficas
 Todos
os mapas são representações
aproximadas da superfície terrestre;
É
impossível representar uma
superfície curva em uma superfície
plana sem que haja deformações.;
 Por
isso os mapas preservam certas
características ao mesmo tempo em
que alteram outras;
Representação da Superfície da
Terra

Globo: Esfera, é uma representação tridimensional do
dado geográfico. Esta representação mais realística
que um mapa planar pois o globo mantém as
propriedades espaciais (área, forma, direção e
distância).

Mapa: é uma representação bidimensional da
superfície curva da Terra. Para expressar um espaço
tridimensional em um mapa bidimensional é
necessário projetar as coordenadas de um espaço
tridimensional para um espaço bidimensional (plano).

Preferência aos mapas: facilidade de uso,
armazenamento, deslocamento, em representar a
superfície terrestre em grandes escalas, etc.
Projeções Cartográficas
 A elaboração
de um mapa requer um
método que estabeleça uma relação
entre os pontos da superfície da Terra e
seus correspondentes no plano de
projeção do mapa;
 Para
se obter essa correspondência,
utilizam-se as projeções cartográficas.
Projeções Cartográficas
Projeção cartográfica é a representação de uma superfície esférica (a
Terra) num plano (o mapa), ou seja, trata-se de um "sistema plano
de meridianos e paralelos sobre os quais pode ser desenhado
um mapa" (Erwin Raisz. Cartografia geral. P. 58).
O grande problema da cartografia consiste em ter de representar
uma superfície esférica num plano, pois, como é sabido, a esfera é
um sólido não-desenvolvível, isto é, não-achatável ou não
planificável. Assim, sempre que achatarmos uma esfera,
necessariamente ela sofrerá alterações ou deformações.
Projeções Cartográficas

Os sistemas de projeções cartográficas foram
desenvolvidos para dar uma solução ao problema da
transferência de uma imagem da superfície curva da
esfera terrestre para um plano da carta, o que sempre
vai acarretar deformações.

Os sistemas de projeções constituem-se de uma
fórmula matemática que transforma as coordenadas
geográficas, a partir de uma superfície esférica
(elipsoidal), em coordenadas planas, mantendo
correspondência entre elas. O uso deste artifício
geométrico das projeções consegue reduzir as
deformações, mas nunca eliminá-las.
Projeções Cartográficas
Todas as projeções apresentam deformações, que podem ser em
relação às distâncias, às áreas ou aos ângulos. Assim, cabe ao
cartógrafo escolher o tipo de projeção que melhor atenda aos objetivos
do mapa.
A maior parte das projeções hoje existentes deriva dos três tipos ou
métodos originais, a saber: cilíndricas, cônicas e planas ou azimutais.
Projeções Cartográficas

Imagine um grande pedaço de papel (a superfície
de projeção) colocado em contato com o globo e
uma fonte de luz brilhando no centro do globo.

Os raios de luz projetam as feições desenhadas na
superfície da esfera, na superfície plana do papel.

As projeções são representações planas da
superfície esférica da Terra, desenhadas sobre o
papel ou exibidas sobre a tela do computador.

Em outras palavras, elas expressam uma superfície
tridimensional em uma superfície bidimensional.
Projeção Cilíndrica




A projeção cilíndrica resulta da projeção dos
paralelos e meridianos sobre um cilindro
envolvente, que é posteriormente desenvolvido
(planificado). Esse tipo de projeção:
apresenta os paralelos retos e horizontais e os
meridianos retos e verticais;
acarreta um crescimento (deformação)
exagerado das regiões de elevadas latitudes;
é o mais utilizado para a representação total da
Terra (mapas-múndi).
Projeção Cilíndrica
Nesta projeção os meridianos e os paralelos
são linhas retas que se cortam em ângulos
retos.
 Nela as regiões polares aparecem muito
exageradas

Projeção Cilíndrica
Tipo de Superfície Adotada
PROJEÇÃO CILÍNDRICA
Projeção Cônica



A projeção cônica resulta da projeção do globo
terrestre sobre um cone, que posteriormente é
planificado. Esse tipo de projeção:
apresenta paralelos circulares e meridianos
radiais, isto é, retas que se originam de um
único ponto;
é usado principalmente para a representação
de países ou regiões de latitudes
intermediárias, embora possa ser utilizado para
outras latitudes.


Nesta projeção os meridianos convergem
para os pólos e os paralelos são arcos
concêntricos situados a igual distância uns
dos outros.
São utilizados para mapas de países de
latitudes médias
Projeção Cônica
Tipo de Superfície Adotada
PROJEÇÃO CÔNICA
Projeção Plana ou Azimutal
A projeção azimutal resulta da projeção da
superfície terrestre sobre um plano a partir de
um determinado ponto (ponto de vista).
 De acordo com Erwin Raisz (famoso
cartógrafo americano), as projeções
azimutais são de três tipos: polar, equatorial e
oblíqua. Elas são utilizadas para confeccionar
mapas especiais, principalmente os náuticos
e aeronáuticos.

Projeção Plana
Tipo de Superfície Adotada
A distorção no mapa aumenta conforme se
distancia do ponto de tangência.
 Considerando que distorção é mínima perto
do ponto de tangência, as projeções
azimutais são apropriadas para representar
áreas que têm extensões aproximadamente
iguais nas direções norte-sul ou leste-oeste.

PROJEÇÃO AZIMUTAL
Projeções cartográficas: quanto as
propriedades espaciais
Quanto ao grau de deformação das superfícies
representadas, são classificadas em:

Conformes ou isogonais: grandezas dos ângulos inalterada.
A forma e a fisionomia entre as regiões representadas no
mapa mantém-se igual àquela da superfície terrestre. Para
conseguir isto, as áreas são alteradas

Equivalentes isométricas : Conserva as áreas, mantém a
proporção de tamanho entre o real e a do desenho . Para tal,
a forma é alterada

Equidistantes: Conserva relação entre comprimentos em
certas direções, só pode ser conseguida em algumas linhas.
Projeções Conformes ou Isogonais

Preserva os ângulos.

Paralelos e os meridianos se
cruzam em ângulos retos

Distorce-se a áreas dos
objetos no mapa

Ex: Mercator
Projeções Equivalentes ou Isométricas
Não deformam áreas, conservando uma relação
constante da área.
 Alteram as formas
Ex: Peters

Brasil:
 4.320km N-S
 4.328km L-O
Peters, cilíndrico equivalente
MERCATOR X PETERS
DIFERENTES VISÕES DO “MUNDO”
São os mapas-múndi mais usados.
 Ambos feitos a partir de projeções cilíndricas.

MERCATOR (1569)
PETERS (1973)
Projeções Eqüidistantes

São as projeções que não
apresentam deformações
em linha reta;

Isso só é possível em
determinada direção.

São menos empregadas
que as projeções
conformes e equivalentes,
porque raramente é
desejável um mapa com
distâncias corretas
apenas em uma direção.

Usadas em rotas aéreas
ou marítimas retas.
ONU
Projeções Geométricas
Classificação quanto ao método de construção.
Se baseiam em princípios geométricos projetivos
são subdivididas em:

Perspectivas: são as obtidas pelas
interseções, sobre determinada superfície,
das retas que passam pelos pontos
correspondentes da superfície da Terra e por
um ponto fixo, denominado ponto de vista.

Pseudo-perspectivas.
Projeções Perspectivas: Ponto de Vista
É sempre considerado como o ponto situado sobre a
direção perpendicular do ponto central da parte da
superfície da Terra que se deseja representar;
 Pode estar disposto a qualquer distância do centro da
Terra (desde o infinito até coincidente com esse
próprio centro).
Três posições principais das Projeções perspectivas:
 Gnomônica – ponto de vista no centro da Terra;
 Estereográfica – ponto de vista na superfície da Terra;
 Ortográfica – ponto de vista no infinito.

Projeções Pseudo-perspectivas
São projeções perspectivas nas quais se recorre a
algum artifício, de maneira a se obter determinada
propriedade.
 Um exemplo desse tipo de projeção é a projeção
cilíndrica equatorial estereográfica, na qual o ponto de
vista não fica fixo, mas vai percorrendo o equador,
situando-se sempre no anti-meridiano do ponto a
projetar.
Sistemas não perspectivos
 Fogem às definições geométricas.
 Projeções modificadas ou pseudoprojeções: são
sistemas resultantes de variações simples dos sistemas
perspectivos.
 Projeções convencionais: pode ser definida uma série de
condições para originá-las, considerando a
representação da totalidade da superfície terrestre,
podendo ser contínuas ou interrompidas.

Projeção de Mercator



Mais conhecida e
empregada, a projeção
cilíndrica direta em
perspectiva tem sido
citada como a de
Mercator de 1569.
Mas, não é!
Na projeção de Mercator,
o ponto de vista não é
fixo, a projeção de cada
paralelo parte de um
ponto cada vez mais
afastado do centro da
esfera.
Projeção de
Mercator
Com isso, o afastamento dos paralelos nas
regiões polares é menor.
 Mercator justificou dizendo que o ponto de vista
variável se trata de uma nova disposição dos
meridianos com referência aos paralelos.
 Ele também não empregou um cilindro tangente
(essa foi uma invenção posterior).

Deformações da Projeção de Mercator





Todos os paralelos possuem o mesmo tamanho (sabe-se
que a circunferência é cada vez menor em direção aos
polos). Assim, deformação leste-oeste conforme aumenta a
latitude;
Todos os meridianos mantém a mesma distância entre si
(na verdade são mais afastados no Equador, encontram-se
nos polos). Assim, deformação leste-oeste conforme
aumenta a latitude;
Os paralelos são mais afastados nas regiões polares (na
realidade mantém afastamento constante) Assim,
deformação no sentido norte-sul conforme aumenta a
latitude
Isso explica as grandes deformações desta projeção em
altas latitudes.
Ex: Groelândia em relação a América do Sul ou África, que
são maiores do que a primeira e na projeção tem
dimensões semelhantes. Isto não acontece em outras
projeções, com proporções de áreas mais reais.
Projeções Cartográficas quanto as propriedades espaciais
Comparação:
Conforme / Equivalente
Proporção no mapa Mercator
Proporção no
mapa Mollweide
Projeções Cartográficas
quanto as propriedades espaciais
Projeções Afiláticas –
- não possui nenhuma das propriedades anteriores.
- equivalência, conformidade e eqüidistância variam
Outros Exemplos de Projeções Cartográficas
Projeção cônica
Projeção Azimutal Eqüidistante Polar
Projeção de Mollweide
Projeção de Goode, que modifica a de Mollweide