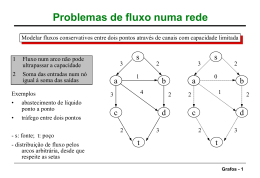
Algoritmos em Grafos
Buscas em Grafos
Prof. André Renato
1º Semestre/2012
Buscas em Grafos
Uma das operações mais comuns em
estruturas de dados consiste em listar os
elementos armazenados de acordo com a
estruturação utilizada.
 Em listas, é possível imprimir os
elementos um após o outro, na mesma
ordem em que se encontram na lista.

Buscas em Grafos

Em árvores binárias, existe três formas de
se imprimir todos os elementos: em
ordem, em pré-ordem e em pós-ordem.
20
15
8
40
19
32
45
Buscas em Grafos
Os algoritmos são simples e utilizam
eficientemente a estrutura recursiva da
árvore.
 Além disso, existe um nó que é diferente
dos demais e através do qual é possível o
percorrimento atingindo todos os demais
nós: nó raiz.

Buscas em Grafos
Em grafos, qual o nó raiz?
 Como é feita a estruturação recursiva do
grafo?
 A segunda pergunta é de difícil resposta,
pois nem sempre o grafo apresenta uma
estruturação bem-definida (na verdade,
quase nunca).
 A primeira pergunta é mais simples: não
existe uma raiz natural em um grafo.

Buscas em Grafos

Como fazer então o percorrimento?
◦ O primeiro passo consiste em escolher um
nó aleatoriamente para ser o ponto inicial do
algoritmo.
◦ Deve-se então adotar uma política para o
processamento do nó inicial e,
sucessivamente, dos seus adjacentes.
◦ Existem duas políticas mais usuais, que dão
origem às duas formas de buscas mais
utilizadas.
Buscas em Grafos

Busca em largura
◦ A idéia consiste em, partindo de um nó inicial
v, armazenar todos os nós u adjacentes a ele.
◦ Escolher um nó u e armazenar todos os
adjacentes;
◦ Passar para o segundo nó u e repetir o
processo até que todos os nós imediatamente
adjacentes a v sejam tratados.
◦ O procedimento se repete para os nós
adjacentes aos nós u armazenados.
Buscas em Grafos

Além do próprio grafo, é necessário
armazenar os nós que estão sendo
processados em outra estrutura de dados.
Qual???
Buscas em Grafos
Ainda existe um problema: normalmente
é possível partir de um nó v e atingir um
nó u de duas ou mais formas diferentes.
 Como evitar que este tipo de
processamento repetido seja evitado sem
excluir previamente nenhuma
possibilidade de acesso aos nós?

Buscas em Grafos
Uma idéia é colocar nos nós um tipo de
marcação que servirá para identificar se o
nó já foi processado ou ainda não.
 Um atributo booleano (ou inteiro) é
suficiente para cada nó.
 Inicialmente, todos os nós são marcados
como “não-visitado”. O nó inicial é
colocado na fila e marcado como visitado.
 O algoritmo prossegue como descrito
anteriormente.

Buscas em Grafos
2
3
1
7
6
8
9
10
4
5
Buscas em Grafos

Busca em profundidade:
◦ A idéia agora é partir de um nó inicial v e
encontrar um primeiro nó adjacente u.
◦ Ao invés de enfileirar o nó u e buscar outro
adjacente a v, mudamos imediatamente para o
primeiro nó u encontrado e repetimos as
operações.
Buscas em Grafos

Busca em profundidade:
◦ Quando um nó u for totalmente explorado,
voltamos o fluxo do algoritmo para o nó que
alcançou u primeiramente.
◦ Prosseguimos, então, com outro nó adjacente
ainda não explorado até que todos os nós
adjacente ao nó inicial tenham sido
explorados.
◦ Neste ponto, o fluxo do algoritmo volta para
o inicial encerrando sua execução.
Buscas em Grafos
A estrutura de fila utilizada na busca em
largura não faz mais sentido, pois os nós
vão sendo processados à medida em que
são encontrados.
 No entanto, por precisar mudar
constantemente o nó corrente e depois
voltar por todos os nós processados até
o nó inicial, outra estrutura é necessária.

Buscas em Grafos
Qual????
 Se vamos utilizar uma pilha, é possível
pensar no algoritmo através de uma
abordagem recursiva?

Buscas em Grafos
2
3
1
7
6
8
9
10
4
5
Buscas em Grafos
Os algoritmos de busca podem revelar
informações importantes sobre os
vértices, as arestas e o próprio grafo
como todo.
 Para conseguir isto, precisamos alterar
levemente os algoritmos, fazendo-os
armazenar informações extras durante
suas execuções.

Buscas em Grafos

Busca em largura:
◦ Distância entre os vértices: pode ser
entendida como a quantidade mínima de
arestas adjacentes entre dois vértices;
◦ Para calcular a distância e quais arestas estão
envolvidas, adicionaremos duas informações
aos vértices: a distância corrente d e o vértice
que o precede na busca pred.
◦ Vale lembrar que a distância não leva em
conta o peso das arestas.
Buscas em Grafos
As arestas indicadas pelo valor de pred
formam uma estrutura de dados
conhecida. Qual?
 Por que isso acontece?

Buscas em Grafos

Busca em profundidade:
◦ Quando um nó é visitado, não temos a menor
idéia de quando o fluxo do algoritmo voltará
para ele.
◦ Isto depende da quantidade de nós que serão
alcançados através dele.
Se imaginarmos que o algoritmo é executado de
acordo com horizonte de tempo fictício onde cada
visita a um nó demora uma unidade de tempo,
podemos anotar quando o nó é começa a ser
visitado e quando termina.
Buscas em Grafos

Busca em profundidade:
◦ Se imaginarmos que o algoritmo é executado
de acordo com horizonte de tempo fictício
onde cada visita a um nó demora uma
unidade de tempo, podemos anotar quando o
nó é começa a ser visitado e quando termina.
◦ Teremos então duas informações além de
pred: o tempo de descoberta do nó desc e o
tempo de finalização do nó fim.
Buscas em Grafos
Os tempos de descoberta e finalização
apresentam uma estrutura de parênteses.
 Se representarmos a descoberta do nó u
pelo símbolo “(u” e a finalização pelo
símbolo “u), a sequência de descobertas e
finalizações gera uma expressão bem
formada, onde os parênteses estão
corretamente aninhados.

Buscas em Grafos

Exemplo de estrutura de parênteses
y
z
s
t
x
w
v
u
s
t
z
y
v
u
w
x
1 2 3 4 5 6 7 8 9 10 1112 13 14 15 16
(s (z (y (x x) y) (w w) z) s) (t (v v) (u u) t)
Buscas em Grafos

Classificação de arestas:
◦ Pode trazer informações importantes sobre o
grafo, como a existência de ciclos (que será
visto posteriormente).
◦ Arestas de árvore: são as arestas obtidas
pela relação de precedência direta entre
vértices do u e v do grafo, ao final da busca.
◦ A aresta (u,v) é de árvore, se v for
descoberto por esta mesma aresta.
Buscas em Grafos

Classificação de arestas:
◦ Arestas de retorno: são as arestas (u,v)
que conectam um vértice u a um vértice v já
visitado anteriormente.
◦ Arestas de avanço: são as arestas (u,v) que
conectam um vértice u a um vértice v
descendente não-imediato.
◦ Arestas de cruzamento: são as demais
arestas do grafo.
Buscas em Grafos
y
z
s
t
x
w
v
u
s
t
z
y
x
v
w
u
Buscas em Grafos
Ordem topológica: pode ser vista como o
posicionamento dos vértices numa linha
horizontal, onde todas as arestas estão da
esquerda para a direita.
 A ordem topológica é aplicada a grafos
direcionados que não possuam ciclos.

Buscas em Grafos
Buscas em Grafos

Algoritmo para ordem topológica:
◦ Executar a busca em profundidade;
◦ Conforme os vértices são finalizados, colocálos na frente de uma lista encadeada*;
◦ Retornar o início da lista;

*Pode ser utilizada uma pilha.
Buscas em Grafos
Componentes fortemente conexos: são
subconjuntos maximais de vértices, onde
para cada par de vértices (u,v), existe
uma forma de chegar de u até v e viceversa.
 Não faz sentido em grafos nãodirecionados. Por quê?????

Buscas em Grafos
1
2
3
5
6
7
8
9
4
Buscas em Grafos

Algoritmo para gerar os componentes:
◦ Executar a busca em profundidade, anotando
os tempos de finalização de cada vértice;
◦ Calcular o grafo transposto;
◦ Aplicar a busca em profundidade no grafo
transposto:
 Considerar os vértices em ordem decrescente de
seus tempos de finalização;
◦ Mostrar os vértices de cada árvore como um
componente fortemente conexo;
Buscas em Grafos

Colocar grafos de exemplo e pseudocodigo no final