UNIVERSIDADE FEDERAL FLUMINENSE - UFF
INSTITUTO DE GEOCIÊNCIAS
PROGRAMA DE PÓS-GRADUAÇÃO EM GEOLOGIA E
GEOFÍSICA MARINHA - MESTRADO
COMPONENTES TENSORIAIS DA ATRAÇÃO GRAVITACIONAL DE UM
PRISMA REGULAR RETANGULAR COM FUNÇÃO DE DENSIDADE
POLINOMIAL CÚBICA
AMÉRICO DOS SANTOS JUNIOR
Dissertação apresentada ao curso de Pós-Graduação
em Geologia e Geofísica Marinha da Universidade
Federal Fluminense, como requisito parcial para
obtenção do Grau de Mestre.
Área de Concentração: Geologia e Geofísica Marinha.
Orientador: Prof. Dr. MARCO POLO PEREIRA BUONORA.
2012
NITERÓI - RJ
S237c
Santos Jr., Américo dos.
Componentes tensoriais da atração gravitacional
de um prisma regular retangular com função de
densidade polinomial cúbica / Américo dos Santos
Junior. - Niterói : [s.n.], 2012.
125 f. ; Ilust.;
Dissertação (Mestrado em Geologia e Geofísica
Marinha) – Universidade Federal Fluminense,
2012.
Bibliografia: f.103-104.
Orientador: Marco Polo Pereira Buonora
1. Geologia e Geofísica Marinha. I. Autor. II.
Título.
CDD 551.468
À minha querida Isabella, pelo amor, à minha
esposa pelo companheirismo e aos meus pais
pelo incentivo aos meus estudos.
AGRADECIMENTOS
Ao meu orientador, Dr. Marco Polo Buonora.
Ao Geofísico Júlio Lyrio da Petrobras, pelo apoio técnico constante a minha
pesquisa.
Ao Geólogo Marcos Munis da CPRM, fonte de conhecimentos.
Ao Geofísico André Rugenski da ANP, por ter compartilhado sua
experiencia comigo.
Ao Geofísico Dionísio Carlos da Vale, pela troca de conhecimentos.
À CPRM, por esta oportunidade para o meu aprimoramento profissional.
À UFF, que me permitiu o desenvolvimento deste estudo.
Ao ON, por ter sido aceito como aluno especial.
À ANP, pela cessão de dados públicos do acervo do BDEP.
7
SUMÁRIO
AGRADECIMENTOS..........................................................................................................7
LISTA DE TABELAS........................................................................................................14
LISTA DE ABREVIATURAS, SIGLAS E SÍMBOLOS...................................................15
RESUMO............................................................................................................................17
ABSTRACT........................................................................................................................18
1 INTRODUÇÃO................................................................................................................19
2 A SOLUÇÃO ANALÍTICA DE JUAN GARCÍA-ABDESLEM....................................21
3 A SOLUÇÃO ANALÍTICA PROPOSTA PARA O TENSOR GRADIENTE .............26
3.1 PROPRIEDADES DO TENSOR GRADIENTE GRAVIMÉTRICO......................26
4 CÁLCULO DAS EQUAÇÕES PARA O TENSOR GRADIENTE................................30
5 VALIDAÇÃO DA SOLUÇÃO ANALÍTICA PROPOSTA...........................................48
5.1 VALIDAÇÃO MATEMÁTICA...............................................................................48
5.2 APLICAÇÃO A UM MODELO SINTÉTICO ........................................................52
5.3 COMPARAÇÃO COM UMA SOLUÇÃO NUMÉRICA........................................58
5.4 CONFRONTAÇÃO COM A FILTRAGEM DO OASIS MONTAJ.......................65
5.5 AVALIAÇÃO COMPORTAMENTAL DA FUNÇÃO CONTRASTE DE
DENSIDADE ..................................................................................................................78
6 APLICAÇÃO DAS EQUAÇÕES DA COMPONENTE TENSORIAL VERTICAL NA
BACIA POTIGUAR .........................................................................................................81
8
6.1 DETERMINAÇÃO DE UMA FUNÇÃO CONTRASTE DE DENSIDADE PARA
A REGIÃO.......................................................................................................................87
6. 2 MODELO DO EMBASAMENTO APROXIMADO PARA A REGIÃO..............90
6.3 APLICAÇÃO DO MODELO DIRETO AO EMBASAMENTO INFERIDO.........95
6.4 DETERMINAÇÃO DO CONTRASTE DE DENSIDADE CONSTANTE............99
7 CONCLUSÕES..............................................................................................................101
8 REFERÊNCIAS BIBLIOGRÁFICAS...........................................................................103
9 APÊNDICES..................................................................................................................105
APÊNDICE 1: PROGRAMA PARA CÁLCULO DAS COMPONENTES TENSORIAIS
............................................................................................................................................105
APÊNDICE 2: SCRIPT PARA GERAÇÃO DOS GRÁFICOS.......................................117
APÊNDICE 3: SCRIPT PARA CÁLCULO DAS INTEGRAIS NUMERICAS............121
APÊNDICE 4: ARQUIVO DE PARAMETROS DO PRISMA.......................................125
9
LISTA DE ILUSTRAÇÕES
FIGURA 1 – ATRAÇÃO GRAVITACIONAL NO PONTO P PROVOCADA POR UMA
DISTRIBUIÇÃO DE MASSA.............................................................................................27
FIGURA 2 – ARRANJO DA FONTE (PRISMA) E DAS ESTAÇÕES (PONTOS) –
VISÃO SUPERIOR.............................................................................................................53
FIGURA 3 – COMPONENTE VERTICAL (UZ) – SOLUÇÃO ANALÍTICA DE
GARCIA-ABDESLEM (2005)............................................................................................54
FIGURA 4 – SOLUÇÃO ANALÍTICA PROPOSTA: (A) COMPONENTE UXX; (B)
COMPONENTE UYY.........................................................................................................55
FIGURA 5 – SOLUÇÃO ANALÍTICA PROPOSTA: (A) COMPONENTE UXZ; (B)
COMPONENTE UYZ.........................................................................................................56
FIGURA 6 – SOLUÇÃO ANALÍTICA PROPOSTA: (A) COMPONENTE UXY; (B)
COMPONENTE UZZ..........................................................................................................57
FIGURA 7 – ARRANJO DA FONTE (PRISMA) E DAS ESTAÇÕES (PONTOS) –
VISÃO SUPERIOR.............................................................................................................60
FIGURA 8 – COMPARAÇÃO ENTRE AS INTEGRAÇÕES ANALÍTICA E
NUMÉRICA PARA A COMPONENTE UXX ..................................................................62
FIGURA 9 – COMPARAÇÃO ENTRE AS INTEGRAÇÕES ANALÍTICA E
NUMÉRICA PARA A COMPONENTE UXY ..................................................................62
10
LISTA DE ILUSTRAÇÕES
FIGURA 10 – COMPARAÇÃO ENTRE AS INTEGRAÇÕES ANALÍTICA E
NUMÉRICA PARA A COMPONENTE UXZ ...................................................................63
FIGURA 11 – COMPARAÇÃO ENTRE AS INTEGRAÇÕES ANALÍTICA E
NUMÉRICA PARA A COMPONENTE UYY ..................................................................63
FIGURA 12 – COMPARAÇÃO ENTRE AS INTEGRAÇÕES ANALÍTICA E
NUMÉRICA PARA A COMPONENTE UYZ ...................................................................64
FIGURA 13 – COMPARAÇÃO ENTRE AS INTEGRAÇÕES ANALÍTICA E
NUMÉRICA PARA A COMPONENTE UZZ ...................................................................64
FIGURA 14 – COMPONENTE UZ TRANSPORTADA PARA O OASIS MONTAJ.....66
FIGURA 15 – SOLUÇÃO ANALÍTICA,COMPONENTE UXX.....................................67
FIGURA 16 – FILTRAGEM NO OASIS MONTAJ/MAGMAP, COMPONENTE: UXX
..............................................................................................................................................68
FIGURA 17 – SOLUÇÃO ANALÍTICA, COMPONENTE: UYY ..................................69
FIGURA 18 – FILTRAGEM NO OASIS MONTAJ/MAGMAP, COMPONENTE: UYY
..............................................................................................................................................70
FIGURA 19 – SOLUÇÃO ANALÍTICA, COMPONENTE: UZZ ...................................71
FIGURA 20 – FILTRAGEM NO OASIS MONTAJ/MAGMAP, COMPONENTE: UZZ
..............................................................................................................................................72
11
LISTA DE ILUSTRAÇÕES
FIGURA 21 – SOLUÇÃO ANALÍTICA, COMPONENTE: UXY ..................................73
FIGURA 22 – FILTRAGEM NO OASIS MONTAJ/MAGMAP, COMPONENTE: UXY
..............................................................................................................................................74
FIGURA 23 – SOLUÇÃO ANALÍTICA, COMPONENTE: UXZ....................................75
FIGURA 24 – FILTRAGEM NO OASIS MONTAJ/MAGMAP, COMPONENTE: UXZ
..............................................................................................................................................76
FIGURA 25 – SOLUÇÃO ANALÍTICA, COMPONENTE: UYZ ...................................77
FIGURA 26 – FILTRAGEM NO OASIS MONTAJ/MAGMAP, COMPONENTE: UYZ
..............................................................................................................................................78
FIGURA 27 – SIMULAÇÕES COM O TERMO INDEPENDENTE DA FUNÇÃO
POLINOMIAL CÚBICA.....................................................................................................80
FIGURA 28 – A BACIA POTIGUAR................................................................................81
FIGURA 29 – MAPA POLÍTICO DA REGIÃO COM LOCALIZAÇÃO DOS POÇOS E
A ÁREA SELECIONADA .................................................................................................84
FIGURA 30 – CARTA DA ANOMALIA BOUGUER DA REGIÃO SELECIONADA .85
FIGURA 31 – COMPORTAMENTO DAS FUNÇÕES CONTRASTE DE DENSIDADE
(A) E DENSIDADE (B) .....................................................................................................89
FIGURA 32 – NUVEM DE PONTOS OBSERVADOS E CURVA AJUSTADA. .........90
12
LISTA DE ILUSTRAÇÕES
FIGURA 33 – EMBASAMENTO INFERIDO PARA A REGIÃO. AZIMUTE: -40º E
ELEVAÇÃO: 32º.................................................................................................................93
FIGURA 34 – MAPA DE CONTORNO DO EMBASAMENTO INFERIDO...................94
FIGURA 35 – COMPONENTE UZZ DO EMBASAMENTO INFERIDO PARA A
REGIÃO...............................................................................................................................96
FIGURA 36 – CARTA DA PRIMEIRA DERIVADA VERTICAL PARA A REGIÃO.. .97
FIGURA 37 – CARTA DE DIFERENÇAS DAS COMPONENTES UZZ .......................98
FIGURA 38 – MAPA DA COMPONENTE UZZ COM DENSIDADE CONSTANTE. 100
13
LISTA DE TABELAS
TABELA 1 – COORDENADAS DA REGIÃO ESTUDADA...........................................83
TABELA 2 – POÇOS SELECIONADOS E PROFUNDIDADE DAS FORMAÇÕES.....86
TABELA 3 – CONTRASTE DE DENSIDADE MÉDIO NA REGIÃO ESTUDADA ....99
14
LISTA DE ABREVIATURAS, SIGLAS E SÍMBOLOS
LISTA DE ABREVIATURAS
f(z)
G
Ik
ki
P
Pn(z)
p
Q
q
r
R
Rn
s
U
Uxx
Uxy
Uxz
Uyy
Uyz
Uz
Uzz
X
x
x0
wi
Y
y
y0
Z
z
Integrando da equação
Constante gravitacional universal
Integração de uma componente da equação da anomalia gravimétrica
i-ésimo zero da função de Legendre
Ponto de observação com as coordenadas cartesianas: x0, y0 e z0.
Polinômio de Legendre
Contraste de densidade na superfície
Ponto de integração
Constante da função polinomial cúbica
Constante da função polinomial cúbica
Distância entre a fonte e o observador
Erro na integração numérica
Constante da função polinomial cúbica
Potencial Gravitacional
Derivada segunda do Potencial Gravitacional na direção Leste-Oeste
Derivada segunda do Potencial Gravitacional na direção Leste-Oeste e Norte-Sul
Derivada segunda do Potencial Gravitacional na direção Leste-Oeste e vertical
Derivada segunda do Potencial Gravitacional na direção Norte-Sul
Derivada segunda do Potencial Gravitacional na direção Norte-Sul e vertical
Derivada primeira do Potencial Gravitacional na direção vertical
Derivada segunda do Potencial Gravitacional na direção vertical
Diferença entre as coordenadas cartesianas leste-oeste da fonte e do observador
Coordenada cartesiana Leste-Oeste da fonte
Coordenada cartesiana Leste-Oeste do observador
Pesos da fórmula de quadratura de Gauss-Legendre
Diferença entre as coordenadas cartesianas Norte-Sul da fonte e do observador
Coordenada cartesiana Norte-Sul da fonte
Coordenada cartesiana Norte-Sul do observador
Diferença entre as coordenadas cartesianas verticais da fonte e do observador
Coordenada cartesiana vertical da fonte
15
z0
Coordenada cartesiana leste-oeste do observador
LISTA DE SIGLAS
DRVX
DRVY
DRVZ
INT
BTWR
SAD69
Filtro de derivada na direção X
Filtro de derivada na direção Y
Filtro de derivada na direção Z
Filtro de integral na direção Z
Filtro Butterworth
Sistema Geodésico regional para a América do Sul
LISTA DE SÍMBOLOS
∆
∇
ρ
Σ
∂
f '(x)
p
t
p
yo
Diferença
Operador Gradiente
Densidade
Somatório
Derivada parcial
Derivada da função f(x)
Vetor p
Vetor transposto de p
Vetor y o
Matriz A
A
t
Matriz transposta de A
A
t −1
 A  Matriz inversa da matriz transposta de A
16
RESUMO
Interpretações gravimétricas utilizam estruturas geométricas simples, cujas equações
para o cálculo da anomalia gravitacional são conhecidas. Uma das formas de se aproximar
o volume de uma estrutura é através de um conjunto de prismas regulares retangulares,
onde a anomalia gravitacional provocada pela estrutura é calculada pela soma dos efeitos
provocados pelos prismas. Entretanto, a utilização de prismas com densidades constantes
afasta a solução do problema da realidade geológica de ambientes sedimentares.
O presente trabalho apresenta uma solução analítica para as componentes tensoriais
(Uxx, Uxy, Uxz, Uyy, Uyz e Uzz) de um prisma regular retangular, com densidade variando
com a profundidade segundo uma função polinomial cúbica. A solução analítica consiste
de 24 equações que foram validadas: matematicamente, em um modelo hipotético
composto de um único prisma, comparando-as a uma solução numérica e confrontando-as
à filtragem de um software estabelecido no mercado.
A componente vertical da solução analítica, Uzz, foi aplicada em um modelo direto em
uma região da bacia Potiguar. Para onde, foram obtidas uma função contraste de densidade
e a topografia do embasamento através de processos de inversão linear e não linear
respectivamente. Simulações entre prismas de densidade constante e variável
demonstraram que a densidade variável apresenta um ganho na resolução de estruturas
geológicas mais profundas.
Palavras chave: Gravimetria, gradiometria, densidade, profundidade, prisma, retangular,
regular
17
ABSTRACT
Interpretations gravity using simple geometric structures, whose equations for
calculating gravitational anomalies are known. One way to approximate the volume of a
structure is through a series of regular rectangular prisms, where the anomaly caused by
the gravitational structure is approximated by the sum of the effects caused by the prisms.
However, the use of prisms with constant density away from the solution of geological
reality of sedimentary environments.
This paper presents an analytical solution for the tensor components (Uxx, Uxy, Uxz,
Uyy, and Uyz Uzz) of a regular rectangular prism with density varying with depth
following a cubic polynomial function. The analytical solution consists of 24 equations
that were validated: mathematically, in a hypothetical model consisting of a single prism,
comparing them to a numerical solution and comparing them to established filtering
software on the market.
The vertical component of the analytical solution, Uzz, was applied to a direct model
in a region of the Potiguar basin. Where were obtained according to a density contrast and
topography of the basement in a process of linear and nonlinear inverting respectively.
Simulations prisms between variable and constant density showed that the gain has a
variable density in the resolution of geologic structures deeper.
Keywords: Gravity, gradiometry, density, depth, prism, rectangular, right .
18
1 INTRODUÇÃO
Prismas regulares retangulares têm desempenhado um papel importante tanto em
problemas diretos quanto em problemas inversos de gravidade, devido à facilidade de
reconstruir geometrias complexas, e a partir daí calcular a atração gravitacional exercida
pelos prismas. O prisma de densidade uniforme tem sido ferramenta útil na interpretação
geofísica, no entanto, em alguns ambientes geológicos, a hipótese de densidade constante
não se sustenta. Um dos principais processos físicos que ocorre durante a evolução
geológica de uma bacia sedimentar é a compactação, onde a densidade aumenta com a
profundidade. Além disso, a estrutura geológica de uma bacia sedimentar pode ser
complicada por outros processos geológicos, tais como a cimentação química, camadas
estratigráficas não uniformes, mudanças de fácies e rupturas estruturais. Devido a esses
processos, modelos
de densidade constante não podem capturar as complexidades
encontradas nas bacias sedimentares. Tais dificuldades foram consideradas no trabalho de
Athy (1930), que relatava que a densidade variava exponencialmente com a profundidade.
Posteriormente, foram propostas algumas abordagens para a representação da variação da
densidade com a profundidade: Cordell (1973), e Chai & Hinze (1988) propuseram uma
função exponencial; Baskara Rao (1986) e Gallardo-Delgado et al. (2003) propuseram uma
função quadrática; Litinsky (1989) introduziu o conceito de função hiperbólica;
Visweswara Rao et al. (1993) sugeriram uma função parabólica; e Garcia-Abdeslem
(2005) propôs uma função polinomial cúbica.
A solução analítica de Garcia-Abdeslem (2005) apresenta o cálculo da atração
gravitacional provada por um prisma retangular retangular com a densidade variando com
a profundidade de acordo com uma função polinomial cúbica. Entretanto, ela contempla
somente a gravimetria convencional. O presente trabalho complementa o método de
Garcia-Abdeslem (2005) apresentando uma solução analítica para as componentes
19
tensoriais. Ademais, a solução analítica apresentada agrega à gradiometria gravimétrica um
modelo mais próximo à realidade estrutural de uma bacia sedimentar.
20
2 A SOLUÇÃO ANALÍTICA DE JUAN GARCÍA-ABDESLEM
Considerando o sistema de coordenadas cartesiano, a componente vertical do campo
gravitacional, Uz, observada em um ponto P  x 0, y 0, z 0  , de uma fonte, um prisma regular
retangular, é representada pela seguinte integral de volume:
Z
Uz  P=G ∫   z  3 dv
R
v
(1)
Onde:
G : Contante Gravitacional Universal = 6,6 x 10 ¹¹ N.m²/kg²;
X =x− x 0 , Y = y− y 0 e Z =z− z 0 : Diferenças entre as coordenadas cartesianas das
fontes e das estações; e
R=   X 2Y 2Z 2  : A distancia entre a fonte e a estação.
A função contraste de densidade possui a seguinte representação:
  z = pqz rz 2sz 3
Onde:
z : representa a profundidade;
p : o contraste de densidade na superfície; e
21
(2)
q,r e s : as constantes da função polinomial cúbica.
Fazendo z =Z  z 0 e considerando que:
2
2
(3)
2
Z  z 0  =Z 2Zz 0Z 0
e ainda que:
3
3
2
2
(4)
3
Z  z 0  =Z 3z 0 Z 3Zz 0 z 0
podemos representar a equação 2 por:
2
  z = pq Z  z 0 r Z z 0 s  Z z 0 
(5)
3
substituindo as equações 3 e 4 na equação 5, obtemos:
2
2
3
2
2
3
(6)
2
3
(7)
  z = pqZ qz 0rZ 2rZz 0rZ 0sZ 3sZ z 03sZz 0Sz 0
2
2
3
  z = pZ  q2rz 03sz 0 Z r 3sz 0 Z  sqz 0rz 0 sz 0
fazendo:
2
3
1= pqz 0 rz 0sz 0
2
2 =q2rz 0 3sz 0
3=r3sz 0
22
(8)
(9)
(10)
(11)
 4=s
substituindo as equações de 8 a 11 na equação 7, podemos representar a função densidade
por:
2
3
  z =1Z 2 Z 3Z 4
(12)
Assim, temos a seguinte representação para a equação 1:
 Z  2 Z 23 Z 34 Z 4 
Uz  P=G ∫ 1
dv
R3
v
(13)
Considerando a propriedade aditiva da integração, podemos reescrever a equação 13:
Z
Z2
Z3
Z4
Uz  P=G 1∫ 3 dv G 2∫ 3 dv G 3∫ 3 dvG 4∫ 3 dv
v R
v R
v R
v R
(14)
a fim de simplificar a equação 14, pode ser escrita como:
(15)
4
Uz  P=G ∑ I k , com k =1,2,3,4
k=1
onde:
Zk
I k =k ∫ 3 dv
v R
Como X =x− x 0 , por propriedade da diferencial:
23
(16)
(17)
dX =d  x− x 0=dx−dx 0
Considerando que x 0 está fora do ponto de integração, dx 0 =0 , resultando em dX=dx.
Analogamente: dy=dY e dz=dZ. Logo, a equação 16 também pode ser escrita como:
x2
y2
(18)
z2
Zk
I k =∫ dX ∫ dY ∫ dZ k 3
R
x1
y1
z1
A integração da equação 18, para o valor de k=1 ao longo de x, y e z resultou na
seguinte equação:
I 1=1 {Z arctan 
(19)
∣∣∣
YX
− X ln Y  R−Y ln X R}
ZR
x2 y2 z 2
x1 y1 z 1
Para o valor de k=2, foi obtida na seguinte equação:
∣∣∣
Z2
XY
Y2
ZX
X2
ZY
I 2= 2 { arctan 
− arctan 
−
arctan 
YX ln  Z R}
2
ZR
2
YR
2
XR
x2 y2 z 2
(20)
x 1 y 1 z1
Para o valor de k=3, foi obtida na seguinte equação:
∣∣∣
Z3
XY
Z3
Y3
2
I 3=3 { arctan 
 lnY R ln  X R XYR}
3
ZR
3
3
3
x2 y2 z 2
(21)
x1 y1 z 1
Para o valor de k=4, foi obtida na seguinte equação:
4
3
3
∣∣∣
Z
Y
X
YZ
ZYR
I 4=4 { ln Y R− ln Z  R−
arctan 

}
2
4
4
XR
4
24
x 2 y 2 z2
x 1 y1 z 1
(22)
Cabe acrescentar que de acordo com Gracia-Abdeslem (2005) as equações acima
foram obtidas, utilizando-se as integrais encontradas em Gradshtein & Ryzhik (1980),
conjuntamente com o método de integração por partes.
25
3 A SOLUÇÃO ANALÍTICA PROPOSTA PARA O TENSOR GRADIENTE
Há dois tipos de levantamentos geofísicos: aqueles que utilizam campos naturais da
terra e aqueles que fazem uso da aplicação de energia artificial na superfície da terra.
Dentre os métodos do primeiro tipo, destacamos a gravimetria que faz uso do campo
gravitacional da terra. O método gravimétrico mede variações na aceleração da gravidade
provocadas por diferenças de densidade nas rochas. Os gravímetros respondem somente a
componente vertical do campo gravitacional, Uz.
A gravimetria gradiométrica difere da gravimetria convencional, pois os gradiômetros
medem gradientes do campo gravimétrico terrestre. Além disso, oferece mais informações
para processo de interpretação, pois responde ao tamanho, forma e densidade da anomalia.
De acordo com Braga (2006), uma importante diferença é que a gradiometria gravimétrica
possui uma largura da faixa de frequência maior que a gravimetria terrestre convencional.
Ainda segundo o autor, o aumento da largura de banda permite a retenção de sinais de alta
frequência gerando feições geológicas rasas e intermediarias, aumentado a resolução dos
corpos.
O gradiente gravimétrico é medido em Eötvös (E), onde 1 E = 0.1 mGal/km.
3.1 PROPRIEDADES DO TENSOR GRADIENTE GRAVIMÉTRICO
Considere os pontos P  x 0, y 0, z 0  e Q x , y , z  , de acordo com Blakely (1996), o
potencial gravitacional, U, obedece ao principio da superposição: O potencial
gravitacional de uma coleção de massas é a soma da atração gravitacional das massas
individuais. Com isso, um corpo pode ser representado pela soma de varias massas
infinitesimais, dm= Q dv , onde  Q é a distribuição de contraste de densidade.
26
Assim, o potencial gravitacional, observado em um ponto P , de um prisma regular
retangular, localizado em Q , considerando a equação 2, é representado por :
U  P =−G ∫
v
dm
dv
=−G∫  Q
R
R
v
(23)
Figura 1 – Atração gravitacional no ponto P provocada por uma distribuição de massa.
Considerando-se o ponto de observação P da figura 1, após ser efetuanda a derivada
parcial do integrando da equação 23 em z 0 a componente vertical da atração gravitacional
de um prisma é:
Uz  P=−G ∫  Q
v
∂ dv
Z
=G ∫   Q 3 dv
∂ z0 R
R
v
(24)
As componentes tensoriais representam taxas de variação da gravidade em uma
determinada direção, elas podem ser obtidas através das segundas derivadas parciais do
integrando da equação 23. Desta forma, podemos calcular:
∂ dv
3X2 1
Uxx  P=−G∫  Q 2 =−G∫  Q 5 − 3 dv
∂ x0 R
R
R
v
v
27
(25)
Uyy  P=−G∫  Q
v
2
∂ dv
3Y
1
=−G ∫  Q 5 − 3 dv
2
∂ y0 R
R
R
v
(26)
∂ dv
3Z2 1
Uzz  P =−G ∫   Q 2 =−G ∫   Q 5 − 3 dv
∂ z0 R
R
R
v
v
(27)
Uxy  P=−G∫  Q
∂ dv
3XY
=−G ∫   Q  5 dv
∂ x0 y0 R
R
v
(28)
Uxz  P=−G ∫   Q 
∂ dv
3XZ
=−G∫  Q 5 dv
∂ x0 z0 R
R
v
(29)
Uyz  P=−G ∫  Q 
∂ dv
3YZ
=−G∫ Q 5 dv
∂ y0 z0 R
R
v
(30)
Uzy  P=−G ∫  Q
∂ dv
3ZY
=−G ∫  Q 5 dv
∂ z0 y0 R
R
v
(31)
Uyx  P=−G∫  Q
∂ dv
3YX
=−G ∫   Q 5 dv
∂ y0 x0 R
R
v
(32)
Uzx  P=−G ∫  Q
∂ dv
3ZX
=−G∫  Q 5 dv
∂ z0 x0 R
R
v
(33)
v
v
v
v
v
v
As 9 componentes do tensor gradiente podem ser distribuídas em uma matriz quadrada
de ordem 3,


Uxx P  Uxy  P Uxz  P
U = Uyx P  Uyy  P Uyz  P
Uzx  P  Uzy P  Uzz  P 
a qual a diagonal principal obedece à equação de Laplace,
28
(34)
Uxx  PUyy  PUzz  P=0
(35)
Uyx  P=Uxy  P ;
Uyz  P=Uzy  P  ; e
Uxz  P=Uzx  P  ;
(36)
além de ser simétrica,
Assim, 6 (seis) componentes do tensor gradiente apresentam equações diferentes: Uxx,
Uxy, Uxz, Uyy, Uyz e Uzz. Considerando-se a equação 35, qualquer uma das componentes
da diagonal principal podem ser obtidas através de operações algébricas com as outras 2
(duas) componentes, por exemplo: Uzz = - (Uxx + Uyy). Como isso, somente 5 (cinco)
componentes do tensor gradiente são linearmente independentes e são medidas nos
gradiômetros.
29
4 CÁLCULO DAS EQUAÇÕES PARA O TENSOR GRADIENTE
A solução apresentada por Garcia-Abdeslem (2005), representada pelas equações de
14 a 22, resolve o problema da densidade variando com a profundidade apenas para a
gravimetria convencional, pois apresenta somente equações para a componente vertical
Uz(P).
Substituindo o valor de   z  da equação 12, na equação 25, ela passa a ser reescrita
como a soma de 4 (quatro) integrais:
2
3X 2 1
3X2 1
1
2 3X
Uxx  P=G  1∫ { 5 − 3 }dv G 2∫ Z { 5 − 3 }dvG 3∫ Z { 5 − 3 }dv
R
R
R
R
R
R
v
v
v
2
3X
1
G  4∫ Z 3 { 5 − 3 }dv
R
R
v
(37)
De uma maneira mais simplificada, a componente Uxx(P) pode ser representada por:
(38)
4
Uxx  P=G ∑ I k , com k =1,2,3,4
k=1
onde cada uma destas integrais tem a seguinte forma:
I k =k ∫ Z
v
k−1
3X 2 1
{ 5 − 3 }dv
R
R
(39)
Fazendo uso das derivadas de Nagy et al. (2000) em conjunto com o teorema
fundamental do calculo, da integral de Banerjee & Gupta (1977), das integrais de Garcia-
30
Abdeslem (2005) e de técnicas de integração foram resolvidas cada uma das 4 (quatro)
integrais da equação 37, cujo detalhamento é apresentado a seguir.
Fazendo k=1, temos:
(40)
3X2 1
I 1 =1∫ { 5 − 3 }dv
R
R
v
Resolvendo a integral da equação 40:
∣∣∣
YZ
I 1 =−1 {arctan 
}
XR
x 2 y 2 z2
(41)
x 1 y1 z 1
Para k=2 :
3X 2 1
I 2= 2∫ Z { 5 − 3 }dv
R
R
v
(42)
Resolvendo a integral da equação 42:
z2 y 2 x 2
3X 2 1
I 2= 2∫ ∫∫ Z { 5 − 3 }dX dY dZ
R
R
z y x
1
1
(43)
1
z2 y2
∣
(44)
∣∣
(45)
XZ
I 2=−2∫ ∫ { 3 }dY dZ
R
z y
1
1
z2
XYZ
I 2=−2∫ { 2
}dz
2
z  X Z  R
1
31
x2
x1
x2 y2
x1 y1
(46)
∣∣∣
I 2=−2 {X ln Y R}
x 2 y 2 z2
x 1 y 1 z1
Para k=3 :
(47)
3X2 1
I 3=3∫ Z { 5 − 3 }dv
R
R
v
2
Resolvendo a integral da equação 47:
z2 y2 x 2
3X2 1
I 3=3∫∫ ∫ Z { 5 − 3 }dX dY dZ
R
R
z y x
(48)
2
1
1
1
z 2 y2
I 3=−3∫ ∫ {
z 1 y1
z2
I 3=−3∫ {
z1
2
∣
(49)
∣∣
(50)
XZ
}dY dZ
R3
2
XYZ
}dZ
 X 2Z 2  R
I 3=−3 { XY ln Z R− X 2 arctan 
x2
x1
x2 y2
x1 y1
∣∣∣
ZY
}
XR
x2 y2 z 2
(51)
x 1 y 1 z1
Finalmente, para k=4 :
I 4= 4∫ Z 3 {
v
3X 2 1
− }dv
R5 R 3
z 2 y2 x2
3X 3 1
I 4= 4∫ ∫ ∫ Z { 5 − 3 }dX dY dZ
R
R
z y x
3
1
1
1
32
(52)
(53)
z2 y 2
I 4=−4 ∫∫ {
z1 y 1
z2
I 4=−4 ∫ {
z1
∣
(54)
∣∣
(55)
∣∣∣
(56)
3
XZ
}dY dZ
3
R
3
XYZ
}dZ
2
 X Z  R
2
x2
x1
x2 y2
x1 y1
I 4=−4 {X 3 ln Y R XYR}
x2 y2 z 2
x 1 y 1 z1
Analogamente, substituindo o valor de   z  da equação 12, na equação 28, ela passa
a ser reescrita como a soma de 4 (quatro) integrais:
Uxy  P=G 1∫
v
3XY
3XYZ
3XYZ2
3XYZ3
dvG

dvG

dvG

dv
2∫
3∫
4∫
R5
R5
R5
R5
v
v
v
(57)
de uma forma mais simplificada:
(58)
4
Uxy  P=G ∑ I k , com k =1,2,3,4
k=1
onde as integrais possuem a forma:
3XYZk −1
I k =k ∫
dv
R5
v
(59)
Na resolução das integrais da equação 57 foram utilizadas as mesmas técnicas usadas
para resolver as integrais da componente Uxx(P), conforme os passos descritos a seguir.
Fazendo k=1, temos:
33
I 1 =1∫
v
(60)
3XY
dv
R5
Resolvendo a integral da equação 60:
∣∣∣
I 1 =1 {ln Z  R}
x 2 y 2 z2
(61)
x1 y 1 z 1
Para k=2 :
I 2= 2∫
v
(62)
3XYZ
dv
5
R
Resolvendo a integral da equação 62:
z2 y 2 x 2
3ZYX
I 2= 2∫ ∫∫
dX dY dZ
5
R
z y x
1
1
1
z2 y 2
−ZY
I 2= 2∫ ∫ { 3 }dY dZ
R
z y
1
(63)
1
z2
Z
I 2= 2∫ { }dZ
R
z
1
∣∣
x2 y2
x2 y2 z 2
x 1 y 1 z1
Para k=3 :
34
(64)
x1
(65)
x1 y1
∣∣∣
I 2= 2 {R}
∣
x2
(66)
(67)
3XYZ 2
I 3=3∫
dv
R5
v
Resolvendo a integral da equação 67:
(68)
z2 y2 x 2
3XYZ 2
I 3=3∫ ∫∫
dX dY dZ
R5
z y x
1
1
1
z2 y2
I 3=3∫∫ {
z1 y1
−YZ
}dY dZ
R3
z2
I 3=3∫ {
z1
2
2
Z
}dZ
R
2
I 3=3 {
(69)
∣
x2
x1
(70)
∣∣
x2 y2
x1 y1
∣∣∣
2
ZR X
Y
−
ln Z R− ln Z R}
2
2
2
x2 y2 z 2
(71)
x1 y1 z 1
Finalmente, para k=4 :
(72)
3XYZ3
I 4= 4∫
dv
5
R
v
Resolvendo a integral da equação 72:
x2 y2 z 2
3XYZ3
I 4= 4∫ ∫ ∫
dX dY dZ
5
R
x y z
1
1
1
z 2 y2
3
−YZ
I 4= 4∫ ∫ { 3 }dY dZ
R
z y
1
(73)
1
35
∣
x2
x1
(74)
z2
I 4= 4∫ {
z1
3
Z
}dZ
R
2
I 4= 4 {
2
(75)
∣∣
x2 y2
x1 y1
2
(76)
∣∣∣
R Z −2X −2Y 
}
3
x2 y2 z 2
x 1 y 1 z1
Outrossim, a substituição de   z  da equação 12, na equação 29, permitiu que ela
fosse reescrita como a soma de 4 (quatro) integrais:
Uxz  P=G 1∫
v
2
3
4
3XZ
3XZ
3XZ
3XZ
dvG 2∫
dvG 3∫
dvG  4∫
dv
5
5
5
R
R
R
R5
v
v
v
(77)
A equação 77 pode ser representada por:
(78)
4
Uxz  P=G ∑ I k , com k =1,2,3,4
k=1
onde:
3XZ k
I k =k ∫
dv
R5
v
(79)
Utilizando-se as mesmas técnicas citadas para a componente Uxx(P), se pôde resolver
cada uma das quatro integrais da equação 77, de acordo com os passos abaixo.
Fazendo k=1, temos:
3XZ
I 1 =1∫ 5 dv
R
v
Resolvendo a integral da equação 80:
36
(80)
(81)
∣∣∣
I 1 =1 {ln Y  R}
x 2 y 2 z2
x1 y 1 z1
Para k=2 :
(82)
3XZ 2
I 2= 2∫ 5 dv
R
v
Resolvendo a integral da equação 82:
(83)
z2 y 2 x 2
3XZ2
I 2= 2∫ ∫∫
dX dY dZ
R5
z y x
1
1
1
z2 y2
I 2=−2∫ ∫ {
z1 y1
z2
2
Z
}dY dZ
R3
2
∣
YZ
I 2=−2∫ { 2
}dZ
2
z Z X R
1
I 2=−2 {Y ln  Z R− X arctan 
(84)
x2
x1
(85)
∣∣
x2 y2
x1 y1
∣∣∣
YZ
}
XR
x 2 y 2 z2
(86)
x 1 y 1 z1
Para k=3 :
I 3=3∫
v
3XZ 3
dv
R5
Resolvendo a integral da equação 87:
37
(87)
z2 y2 x 2
3XZ 3
I 3=3∫ ∫∫ 5 dX dY dZ
R
z y x
1
1
(88)
1
z 2 y2
Z3
I 3=−3∫ ∫ { 3 }dY dZ
R
z y
1
1
∣
x2
x1
∣∣
(90)
∣∣∣
(91)
z2
YZ 3
I 3=−3∫ { 2
}dZ
 Z  X 2 R
z
1
2
(89)
I 3=−3 {YR X ln Y R}
x2 y2
x1 y1
x 2 y 2 z2
x 1 y 1 z1
Finalmente, para k=4 :
(92)
3XZ 4
I 4= 4∫
dv
R5
v
Resolvendo a integral da equação 92:
z2 y 2 x 2
I 4=3 4 ∫ ∫∫
z1 y 1 x 1
XZ 4
dX dY dZ
R5
z2 y 2
∣
(94)
∣∣
(95)
Z4
I 4=−4 ∫∫ { 3 }dY dZ
R
z y
1
1
z2
YZ 4
I 4= 4∫ { 2
}dZ
 Z  X 2 R
z
1
38
(93)
x2
x1
x2 y2
x1 y1
I 4=−4 {X 3 arctan 
2
∣∣∣
YZ
YZR
3XY

−Y 2 ln Z  R−
ln Z  R}
XR
2
2
x 2 y 2 z2
(96)
x1 y 1 z 1
Da mesma forma, a substituição de   z  da equação 12, na equação 26, permitiu
que ela pudesse ser reescrita como a soma de 4 (quatro) integrais:
Uyy  P=G 1∫ {
v
2
3Y 2 1
3Y2 1
1
2 3Y
−
}dv
G

Z
{
−
}dvG

Z
{
− 3 }dv
2∫
3∫
5
3
5
3
5
R
R
R
R
R
R
v
v
2
3Y
1
G  4∫ Z 3 { 5 − 3 }dv
R
R
v
(97)
A representação simplificada da equação 97 seria:
(98)
4
Uyy  P=G ∑ I k , com k =1,2,3,4
k=1
onde:
I k =k ∫ Z
k−1
v
3Y 2 1
{ 5 − 3 }dv
R
R
(99)
A partir das técnicas usadas para a componente Uxx(P), a resolução da equação 99 foi
obtida de acordo com os passos abaixo.
Assim, para k=1, temos:
3Y 2 1
I 1 =1∫ { 5 − 3 }dv
R
R
v
Resolvendo a integral da equação 100:
39
(100)
I 1 =−1 {arctan 
∣∣∣
XZ
}
YR
x2 y2 z 2
(101)
x1 y1 z 1
Para k=2 :
3Y 2 1
I 2= 2∫ Z { 5 − 3 }dv
R
R
v
(102)
Resolvendo a integral da equação 102:
z2 x 2 y 2
3Y2 1
I 2= 2∫ ∫∫ Z { 5 − 3 }dY dX dZ
R
R
z x y
1
1
(103)
1
z2 y2
I 2=−2∫ ∫ {
z1 y1
YZ
}dX dZ
R3
z2
XYZ
I 2=−2∫ { 2
}dZ
2
z Y Z  R
1
∣
y2
(104)
y1
∣∣
x2 y2
(105)
x 1 y1
∣∣∣
(106)
3Y 2 1
− }dv
R 5 R3
(107)
I 2= 2 {Y ln  X R}
x2 y2 z 2
x1 y1 z 1
Para k=3 :
I 3=3∫ Z 2 {
v
Resolvendo a integral da equação 107:
40
z2 y2 x 2
3Y2 1
I 3=3∫ ∫∫ Z { 5 − 3 }dX dY dZ
R
R
z y x
(108)
2
1
1
1
z 2 x2
YZ 2
I 3=−3∫ ∫ { 3 }dX dZ
R
z x
1
1
z2
XYZ 2
I 3=−3∫ { 2
}dZ
 X Z 2  R
z
1
∣
(109)
y2
y1
(110)
∣∣
y2 x2
y1 x1
∣∣∣
ZX
I 3=−3 { XY ln Z R−Y arctan 
}
YR
2
y 2 x 2 z2
(111)
y 1 x1 z1
Finalmente, para k=4 :
3Y 2 1
I 4= 4∫ Z { 5 − 3 }dv
R
R
v
3
z 2 y2 x2
3Y 3 1
I 4= 4∫ ∫ ∫ Z { 5 − 3 }dY dX dZ
R
R
z y x
(112)
(113)
3
1
1
1
z2 x 2
YZ 3
I 4=−4 ∫∫ { 3 }dX dZ
R
z x
1
1
z2
XYZ 3
I 4=−4 ∫ { 2
}dZ
2
Y Z  R
z
1
3
∣
y2
y1
∣∣
(115)
∣∣∣
(116)
y 2 x2
y1 x 1
I 4=−4 {Y lnY R XYR}
x2 y2 z 2
x 1 y 1 z1
41
(114)
De uma maneira similar, após a substituição de   z  da equação 12, na equação 30,
ela foi reescrita como a soma de 4 (quatro) integrais:
3YZ
3YZ 2
3YZ3
3YZ 4
Uyz  P=G 1∫ 5 dvG 2∫
dvG

dvG

dv
3∫
4∫
R
R5
R5
R5
v
v
v
v
(117)
A representação simplificada da componente Uyz(P) seria:
(118)
4
Uyz  P=G ∑ I k , com k =1,2,3,4
k=1
onde:
I k =k ∫
v
3YZ k
dv
R5
(119)
Usando as técnicas utilizadas para a componente Uxx(P), podemos chegar a resolução
de cada uma destas integrais, conforme as etapas abaixo.
Para k=1, temos:
I 1 =1∫
v
3YZ
dv
5
R
(120)
Resolvendo a integral da equação 120:
∣∣∣
I 1 =1 {ln  X  R}
x 2 y 2 z2
x 1 y1 z 1
Para k=2 :
42
(121)
(122)
3YZ 2
I 2= 2∫ 5 dv
R
v
Resolvendo a integral da equação 122:
(123)
z2 y 2 x 2
3YZ2
I 2= 2∫ ∫∫
dY dX dZ
R5
z y x
1
1
1
z2 x 2
I 2=−2∫ ∫ {
z 1 x1
2
Z
}dX dZ
R3
z2
2
∣
XZ
I 2=−2∫ { 2
}dZ
2
z  X Y  R
1
I 2=−2 {X ln  Z R−Y arctan 
(124)
y2
y1
(125)
∣∣
y2 x2
y1 x1
∣∣∣
XZ
}
YR
y2 x2 z 2
(126)
y 1 x 1 z1
Para k=3 :
(127)
3YZ 3
I 3=3∫
dv
5
R
v
Resolvendo a integral da equação 127:
z2 x 2 y 2
3YZ 3
I 3=3∫ ∫∫ 5 dY dX dZ
R
z x y
1
1
(128)
1
z 2 x2
I 3=−3∫ ∫ {
z 1 x1
3
Z
}dX dZ
R3
43
∣
y2
y1
(129)
z2
I 3=−3∫ {
z1
∣∣
(130)
∣∣∣
(131)
x2 y2
3
XZ
}dZ
2
 X Y  R
2
x1 y1
x 2 y 2 z2
I 3=−3 { XRY 2 ln  X  R}
x 1 y1 z 1
Finalmente, para k=4 :
(132)
4
3YZ
I 4= 4∫
dv
5
R
v
Resolvendo a integral da equação 132:
(133)
z2 x 2 y 2
YZ 4
I 4=3 4 ∫ ∫∫ 5 dY dX dZ
R
z x y
1
1
1
z2 x 2
I 4=−4 ∫∫ {
z1 x 1
z2
I 4=−4 ∫ {
z1
I 4=−4 {Y 3 arctan 
4
Z
}dX dZ
R3
4
∣
XZ
}dZ
 X Y 2  R
2
(134)
y2
y1
(135)
∣∣
x2 y2
x1 y1
2
∣∣∣
XZ
XZR
3XY

− X 2 ln  Z R−
ln  Z R}
YR
2
2
x 2 y 2 z2
(136)
x 1 y 1 z1
Igualmente, a substituição de   z  da equação 12, na equação 27, conduziu a soma
das 4 (quatro) integrais abaixo:
44
3Z2 1
3Z 2 1
3Z2 1
Uzz  P =G 1∫ { 5 − 3 }dvG  2∫ Z { 5 − 3 }dvG 3∫ Z 2 { 5 − 3 }dv
R
R
R
R
R
R
v
v
v
2
3Z
1
G  4∫ Z 3 { 5 − 3 }dv
R
R
v
(137)
Ou seja, a componente Uzz(P), pode ser representada por:
(138)
4
Uzz  P =G ∑ I k , com k =1,2,3,4
k=1
onde:
I k =k ∫ Z k−1 {
v
3Z 2 1
− }dv
R5 R 3
(139)
Com as técnicas citada na resolução da componente Uxx(P), a integração foi obtida
conforme descrito abaixo.
Assim, para k=1, temos:
3Z2 1
I 1 =1∫ { 5 − 3 }dv
R
R
v
(140)
Resolvendo a integral da equação 140:
∣∣∣
XY
I 1 =−1 {arctan 
}
ZR
x2 y2 z 2
(141)
x 1 y 1 z1
Para k=2 :
3Z 2 1
I 2= 2∫ Z { 5 − 3 }dv
R
R
v
45
(142)
Resolvendo a integral da equação 142:
(143)
x 2 y 2 z2
3Z2 1
I 2= 2∫ ∫∫ Z { 5 − 3 }dZ dY dX
R
R
x y z
1
1
1
∣
(144)
∣∣
(145)
x2 y2
Z2 1
I 2=−2∫ ∫ { 3  }dY dX
R R
x y
1
1
x2
YZ 2
I 2=−2∫ { 2
}dX
2
x  X Z  R
1
z2
z1
y 2 z2
y 1 z1
(146)
∣∣∣
I 2=−2 {X ln Y RY ln  X R}
x2 y2 z 2
x 1 y 1 z1
Para k=3 :
(147)
3Z2 1
I 3=3∫ Z { 5 − 3 }dv
R
R
v
2
Resolvendo a integral da equação 147:
(148)
z 2 y2 x 2
3Z2 1
I 3=3∫ ∫∫ Z { 5 − 3 }dX dY dZ
R
R
z y x
2
1
1
1
x 2 y2
−Z 3
2Z
I 3=3∫ ∫ { 3 2ln  Z R− }dY dX
R
R
x y
1
1
x2
∣
z1
−YZ 3
ZY
I 3=3∫ { 2
2Yln  Z R−2X arctan 
}dX
2
XR
x  X Z  R
1
46
(149)
z2
∣∣
y 2 z2
y 1 z1
(150)
I 3=−3 {Y 2 arctan 
∣∣∣
ZX
ZY
 X 2 arctan 
−2XY ln  Z R}
YR
XR
x 2 y 2 z2
(151)
x 1 y1 z 1
Finalmente, para k=4 :
(152)
3Z 2 1
I 4= 4∫ Z { 5 − 3 }dv
R
R
v
3
(153)
z 2 y2 x2
3Z 3 1
I 4= 4∫ ∫ ∫ Z { 5 − 3 }dY dX dZ
R
R
z y x
3
1
1
x2 y2
1
4
2
2
−Z
Z
 X Y 
I 4= 4∫ ∫ { 3 − 5R
}dY dX
R
R
R
x y
1
x2
I 4= 4∫ {
x1
1
∣
z2
z1
∣∣
(155)
∣∣∣
(156)
4
−YZ
3YR3X 2 ln Y R}dX
2
2
 X Z  R
I 4= 4 { X 3 ln Y RY 3 ln  X R2XYR }
y2 z 2
y1 z 1
x2 y2 z 2
x 1 y 1 z1
47
(154)
5 VALIDAÇÃO DA SOLUÇÃO ANALÍTICA PROPOSTA
5.1 VALIDAÇÃO MATEMÁTICA
A equação 35 representa uma das propriedade do tensor gradiente. A partir dela,
podemos efetuar a soma das equações 25, 26 e 27, cuja representação seria:
v
2
2
3X
1
3Z
1
− 3 }dvG ∫   z { 5 − 3 }dv
5
R
R
R
R
v
2
3Y
1
G∫   z { 5 − 3 }dv=0
R
R
v
G ∫   z  {
(157)
Considerando as equações 38, 39, 58, 59, 78, 79, 98, 99, 118 e 119, a equação 157,
pode ser representada por:
4
G ∑ { k ∫ Z
k =1
v
k −1
2
2
3X2 1
1
1
k −1 3Y
k−1 3Z
[ 5 − 3 ]dv ∫ Z [ 5 − 3 ] dv∫ Z [ 5 − 3 ]dv }=0
R
R
R
R
R
R
v
v
, com k =1,2,3,4
(158)
fazendo k=1,
3X 2 1
3Z2 1
3Y2 1
G 1 {∫ [ 5 − 3 ]dv∫ [ 5 − 3 ] dv∫ [ 5 − 3 ] dv}=0
R
R
R
R
R
R
v
v
v
(159)
considerando a propriedade aditiva da integração, equação 159 poderia ser representada
por:
48
G 1 ∫ {
v
3 X 2Y 2Z 2 3
− 3 }dv=0
R5
R
(160)
para k=2,
3X 2 1
3Z 2 1
3Y 2 1
G 2 {∫ [ 5 − 3 ] Z dv∫ [ 5 − 3 ]Z dv∫ [ 5 − 3 ]Z dv }=0
R
R
R
R
R
R
v
v
v
(161)
considerando a propriedade aditiva da integração para a equação 161:
3 X 2Y 2Z 2  3
G 2 ∫ {
− 3 }Z dv=0
5
R
R
v
(162)
para k=3,
G 3 {∫ [
v
3X 2 1 2
3Z 2 1 2
3Y 2 1 2
−
]
Z
dv
[
−
]Z
dv
[
∫ R5 R3
∫ R5 − R3 ]Z dv }=0
R5 R3
v
v
(163)
considerando a propriedade aditiva da integração para a equação 163:
3 X 2Y 2Z 2 3
2
G 3∫ {
− 3 }Z dv=0
5
R
R
v
(164)
3X2 1 3
3Z 2 1 3
3Y 2 1 3
G  4 {∫ [ 5 − 3 ] Z dv∫ [ 5 − 3 ]Z dv∫ [ 5 − 3 ]Z dv }=0
R
R
R
R
R
R
v
v
v
(165)
para k=4,
considerando a propriedade aditiva da integração para a equação 165:
49
G  4∫ {
v
3  X 2Y 2Z 2  3
3
− 3 } Z dv=0
5
R
R
(166)
Notem que a equação 158 representa a soma das equações 160, 162, 164 e 166, logo:
3  X 2 Y 2Z 2  3
3 X 2Y 2Z 2 3
G {1 234 }∫ {
−
}{
− 3 }Z
R5
R3
R5
R
v
2
2
2
2
2
2
3 X Y Z  3
3  X Y Z  3
{
− 3 }Z 2{
− 3 } Z 3 dv=0
5
5
R
R
R
R
(167)
fazendo o termos constante da equação, K =G {1 234 } e considerando que se
2
2
2
2
R=   X 2Y 2Z 2  , logo R = X Y Z  . A equação 167 pode ser reescrita como:
3R2 3
3R 2 3
3R 2 3
3R 2 3
K ∫ {[ 5 − 3 ][ 5 − 3 ] Z[ 5 − 3 ] Z 2[ 5 − 3 ]Z 3 }dv=0
R
R
R
R
R
R
R
R
v
K ∫ {[
v
3 3
3
3
3
3
3 3
− 3 ][ 3 − 3 ] Z [ 3 − 3 ] Z 2 [ 3 − 3 ]Z 3 }dv =0
3
R R
R R
R R
R R
K ∫ {0}{0}Z {0}Z 2{0}Z 3 dv=0
(168)
(169)
(170)
v
K ∫ {0}dv=0
(171)
v
aplicando-se a propriedade da constante da integração, a equação 171 resultaria em:
(172)
0=0
demonstrando que a relação obedece à equação de Laplace.
Avaliando, também, os resultados com base nas equações obtidas através das
integrações para as componentes Uxx, Uyy e Uzz.
50
A soma das equações 41, 106 e 141 resulta em:
−1 {arctan 
∣∣∣
XY
ZY
ZX
arctan 
arctan 
}
ZR
XR
YR
x 2 y 2 z2
(173)
=0
x1 y 1 z 1
De fato de acordo com Zhang et. al. (2000), a proposição acima é verdadeira.
Para as demais integrais, pela simples soma algébrica podemos observar os resultados.
A soma das equações 46, 102 e 146 resulta em:
∣∣∣
2 {Y ln X R X ln Y R−Y ln X R− X ln Y R}
x 2 y 2 z2
(174)
=0
x 1 y 1 z1
Efetuando-se a soma das equações 51, 111 e 151, temos:
3 {−2YX ln Z RY 2 arctan 
−3 {Y 2 arctan 
ZX
ZY
 X 2 arctan 
2YX ln Z R}
YR
XR
∣∣∣
ZX
ZY x 2
 X 2 arctan 
}
YR
XR
y 2 z2
(175)
=0
x1 y 1 z 1
Por fim, com a soma das equações 56, 116 e 156 obtém-se:
 4 {Y 3 lnY R X 3 ln  X  R2XYR−Y 3 ln Y  R− X 3 ln X R}
∣∣∣
− 4 {2XYR }
x 2 y 2 z2
(176)
=0
x1 y 1 z1
A soma das equações de 173 a 176 corresponde a mesma soma da equação 158, pois
estas equações representam os resultados das integrações. Logo, UxxUyyUzz =0 a
partir dos resultados das integrações, atendendo também a equação de Laplace.
51
Uma outra propriedade do tensor gradiente é a simetria. Considerando a propriedade
comutativa da multiplicação, as equações 28 e 32 seriam iguais. Assim como o par de
equações 29 e 33 e o par de equações 30 e 31. Notem que seriam obtidos os mesmos
resultados nas integrações.
Uyx  P=G ∫    z 
3YX
3XY
dv=G ∫    z  5 dv=Uxy  p 
5
R
R
v
(177)
Uzx  P=G ∫    z 
3ZX
3XZ
dv =G∫   z  5 dv =Uxz  p
5
R
R
v
(178)
Uzy  P=G ∫    z 
3ZY
3YZ
dv =G∫   z  5 dv =Uyz  p
5
R
R
v
(179)
v
v
v
Podemos concluir a partir das equações 177, 178 e 179 que há simetria entre os pares.
5.2 APLICAÇÃO A UM MODELO SINTÉTICO
A partir dos estudos de Li (2001), Garcia-Abdeslem (2005) propôs a equação 180 para
representar a densidade através de uma função polinomial cúbica no “Green Canion”,
localizado no estado americano de Louisiana, no Golfo do México:
2
3
  z =−747,7203,435 z−26,764 z 1,4247 z kg /m³ 
(180)
onde a profundidade, z, encontra-se em quilômetros, km.
Considere o modelo abaixo de um levantamento terrestre, onde as estações são
representas pelos pontos verdes:
52
Figura 2 – Arranjo da fonte (prisma) e das estações (pontos) – visão superior
Na figura 2, um prisma regular retangular, com 10 km de extensão, nas direções
Leste-Oeste e Norte-Sul, com 8 km de profundidade, cuja densidade varia com a
profundidade de acordo com a equação 180, foi situado a partir do plano z = 0, nas
coordenadas inicias Leste = 10 km e Norte = 10 km. As estações foram situadas a 15 cm
acima do solo e espaçadas com intervalo de 1 km, nas direções Leste e Norte. Totalizando
900 pontos de medição.
Com o método de Garcia-Abdeslem (2005), foi obtida a anomalia da figura 3, que
representa a componente vertical da gravimetria convencional.
53
C o m p o n e n te U z
m G al
30
-1 0
-1 5
25
-2 0
-2 5
20
-3 0
N o rte (k m )
-6 0
-3 5
15
-4 0
-5 0
-4 5
-2 0
-1 0
10
-5 0
-5 5
5
-6 0
0
0
5
10
15
L e s te (k m )
20
25
30
-6 5
Figura 3 – Componente vertical (Uz) – Solução analítica de Garcia-Abdeslem (2005)
Para as componentes tensoriais da solução analítica proposta foram obtidos os
resultados das figuras 4 a 6:
54
(a )
E ö tvö s
30
100
80
0
25
60
40
20
N o rte (k m )
20
0
15
100
0
100
-2 0
10
-4 0
-6 0
5
-8 0
0
-1 0 0
0
0
5
10
15
L e s t e (k m )
20
25
30
(b )
E ö tvö s
30
100
80
0
25
60
N o rte (k m )
40
0
20
100
20
0
15
-2 0
100
10
0
-4 0
-6 0
0
5
-8 0
-1 0 0
0
0
5
10
15
L e s te (k m )
20
25
30
Figura 4 – Solução Analítica proposta: (a) Componente Uxx; (b) Componente Uyy
55
(a )
E ö tvö s
30
100
0
25
50
50
20
N o rte (k m )
50
0
15
100
-1 0 0
-5 0
-5 0
10
-1 0 0
5
0
0
0
5
10
15
L e s te (k m )
20
25
30
(b )
E ö tvö s
30
100
25
50
50
50
20
100
N o rte (k m )
0
15
0
0
-5 0
10
-5 0
-1 0 0
-5 0
-1 0 0
5
0
0
5
10
15
L e s te (k m )
20
25
30
Figura 5 – Solução Analítica proposta: (a) Componente Uxz; (b) Componente Uyz
56
(a )
E ö tvö s
30
60
40
25
20
0
60
40
-6 0
N o rte (k m )
20
20
-4 0
-2 0
0
0
15
0
-2 0
10
20
40
-6 0
-4 0
-2 0
60
-4 0
5
-6 0
0
0
0
5
10
15
L e s te (k m )
20
25
30
(b )
E ö tvö s
30
50
25
0
N o rte (k m )
20
-2 0 0
-2 0 0
-5 0
15
-1 0 0
-2 0 0
10
-2 0 0
0
-1 5 0
5
-2 0 0
0
0
5
10
15
L e s te (k m )
20
25
30
Figura 6 – Solução Analítica proposta: (a) Componente Uxy; (b) Componente Uzz
57
As figuras 4a e 4b apresentam variações no campo gravitacional nas arestas do prisma.
A primeira no sentido Leste-Oeste e a segunda no sentido Norte-Sul.
As figuras 5a e 5b de acordo com Murphy (2004) identificam os centros de massa das
anomalias.
Na figura 6a, observamos a anomalia gravitacional associada aos “cantos” do prisma e
na figura 6b apresenta as variações verticais do campo gravitacional. Observa-se nesta
última componente que as bordas do prisma ficarão mais realçadas.
5.3 COMPARAÇÃO COM UMA SOLUÇÃO NUMÉRICA
Garcia-Abdeslem (1992) propôs uma metodologia que combina integração analítica e
numérica. Na metodologia a anomalia vertical provocada por um prisma pode ser
representada por uma única integral em torno de Z, que foi obtida a partir de integrações
em torno de X e Y na equação 1, resultando na equação 181 .
z2
XY
Uz  P=G ∫ {  z  arctan 
}dZ
ZR
z
1
∣∣
x2 y2
(181)
x 1 y1
A integral da equação 181 pode ser resolvida pelo método numérico, baseado na
fórmula da quadratura de Gauss-Legrendre.
Desta forma, a equação 181 seria reduzida a:
z −z n
Uz  P=G  1 2  ∑ wi f  z i Rn
2
i=1
onde:
f  z i  é o integrando da equação 181;
Rn é o erro de integração;
n é o numero de pontos onde o integrando é avaliado; e
58
(182)
w i=
(183)
2
2
1−k i [P n '  k i ]2
onde:
P n ' k i  é uma função de Lengendre do primeiro tipo; e
k i é o i-ésimo zero da função de Lengendre do primeiro tipo.
Considerando o teorema fundamental do cálculo, as derivadas propostas em Nagy et
al. (2000) representam as integrações ao longo de X e Y nas equações de 25 a 30. Desta
forma, as seis componentes tensoriais podem ser representadas pelas seguintes equações
para este método:
∣∣
z2
x2 y2
XY
1
Uxx  P=G ∫ {  z 
 2
}dz
R X Z 2
z
1
z2
−1
Uxy  P=G ∫ {  z 
}dz
R
z
1
x 1 y1
(185)
∣∣
x2 y2
x1 y1
z2
−YZ
1
Uxz  P=G ∫ {  z
 2
}dz
R X Z 2
z
1
∣∣
x2 y2
x2 y2
XY
1
Uyy  P=G ∫ {  z 
 2
}dz
R Y Z 2
z
1
− XZ
1
Uyz  P=G ∫ {  z
 2
}dz
R Y Z 2
z
1
59
(187)
x 1 y1
∣∣
z2
(186)
x1 y1
∣∣
z2
(184)
x2 y 2
x 1 y1
(188)
∣∣
z2
− XY
1
1
Uzz  P =G∫ {   z 
 2
 2
}dz
2
R
X Z
Y Z 2
z
1
x2 y 2
(189)
x 1 y1
Analogamente ao método de Garcia-Abdeslem (1992), os integrandos das equações de
184 a 189 corresponderão à função, f  z i  , na fórmula da quadratura de Gauss-Legendre.
Para análise dos resultados obtidos, conforme a figura 7, foram selecionados os perfis
A-A' para as componentes: Uxx, Uxy, Uxz e Uzz; e o perfil B-B' para as componentes: Uyy
e Uyz.
Figura 7 – Arranjo da fonte (prisma) e das estações (pontos) – visão superior
Buscando avaliar a dispersão entre a solução analítica e a numérica foi utilizado o chiquadrado, χ². Tal medida estatística representa um teste de hipótese que avalia a dispersão
60
entre duas frequências, uma observada e a outra esperada. Haverá associação entre as duas
frequências, se a dispersão entre elas for mínima. A fórmula do chi-quadrado se encontra
representada pela equação 190.
n
 fo i− fe i 
 =∑
fe i
i =1
2
(190)
em que: f i é a frequência observada;
f i é a frequência esperada; e
n é o numero de observações.
Considerando-se a solução analítica como frequência observada e a solução numérica
como a frequência esperada, deseja-se que os seus valores da solução analítica estejam os
mais próximos possíveis dos valores da solução numérica.
Podemos trabalhar com duas hipóteses para cada uma das componentes tensoriais:
H0: há associação entre a solução analítica e a numérica.
H1: não há associação entre as duas soluções.
Foram selecionadas 30 valores (observações) da solução analítica, o que resulta em
um grau de liberdade, GL, igual a 29, ou seja, GL = 30 -1. Para um número de observações
menores ou iguais a 30, segundo Freitas & Calça (2007, p. 124), deve-se utilizar a
distribuição t de Student. De acordo com a tabela t de Student, para um intervalo de
confiança de 50%, o valor crítico de chi-quadrado, χ², de 0,68304. Para a interpretação dos
resultados obtidos, as componentes cujos valores do χ² estejam acima do valor critico serão
rejeitadas.
As figuras de 8 a 13 apresentam os valores obtidos na integração analítica e numérica.
Nos gráficos, além do comportamento das funções para cada uma das soluções, encontrase a o valor do χ².
61
C o m p o n e n te U x x
150
A n a litic a
N u m e ric a
A m p litu d e (E ö tv ö s )
100
50
0
χ
2 = 0 .0 0 1 2 2 6 1
-5 0
-1 0 0
-1 5 0
0
5
10
15
L e s te (k m )
20
25
30
Figura 8 – Comparação entre as integrações analítica e numérica para a componente Uxx
C o m p o n e n te U x y
15
A n a litic a
N u m e ric a
10
A m p lit u d e (E ö t v ö s )
5
2
χ = 0 .0 0 1 3 1 4 6
0
-5
-1 0
-1 5
0
5
10
15
L e s te (k m )
20
25
30
Figura 9 – Comparação entre as integrações analítica e numérica para a componente Uxy
62
C o m p o n e n te U x z
150
A n a lit ic a
N u m e ric a
A m p lit u d e (E ö t v ö s )
100
50
2
χ = 0 .0 0 1 0 6 8 5
0
-5 0
-1 0 0
-1 5 0
0
5
10
15
L e s te (k m )
20
25
30
Figura 10 – Comparação entre as integrações analítica e numérica para a componente Uxz
C o m p o n e n te U y y
150
A n a lit ic a
N u m e ric a
A m p litu d e (E ö tv ö s )
100
50
0
χ
2 = 0 .0 0 1 2 3 7 6
-5 0
-1 0 0
-1 5 0
0
5
10
15
N o rte (k m )
20
25
30
Figura 11 – Comparação entre as integrações analítica e numérica para a componente Uyy
63
C o m p o n e n te U y z
150
A n a litic a
N u m e ric a
100
A m p litu d e (E ö tv ö s )
50
2
χ = 0 .0 0 1 2 1 9 8
0
-5 0
-1 0 0
-1 5 0
0
5
10
15
N o rte (k m )
20
25
30
Figura 12 – Comparação entre as integrações analítica e numérica para a componente Uyz
C o m p o n e n te U z z
100
A n a lit ic a
N u m e ric a
50
2
χ = 0 .0 0 1 3 6
A m p litu d e (E ö tv ö s )
0
-5 0
-1 0 0
-1 5 0
-2 0 0
0
5
10
15
L e s te (k m )
20
25
30
Figura 13 – Comparação entre as integrações analítica e numérica para a componente Uzz
64
Evidentemente, podemos observar nas figuras de 8 a 13 que tanto a solução analítica
quanto a numérica se comportaram de maneira semelhante. Alem disso, todos os valores
são menores que valor crítico de chi-quadrado, χ², implicando na aceitação da hipótese H0
( há associação entre a solução analítica e a numérica).
5.4 CONFRONTAÇÃO COM A FILTRAGEM DO OASIS MONTAJ
Buscando complementar a avaliação da solução analítica proposta, as respostas ao
modelo obtidas na seção 5.2 foram comparadas com aquelas obtidas em um software de
uso comum no mercado.
Os dados calculados para a componente Uz, obtida através das equações de GarciaAbdeslem (2005), foram transportada para o software Oasis Montaj da Geosoft gerando o
mapa da figura 14.
65
Figura 14 – Componente Uz transportada para o Oasis Montaj.
Utilizando-se a extensão MAGMAP do Oasis Montaj, foram aplicados os filtros de
primeira derivada DRVZ (derivada na direção z), DRVX (derivada na direção x) e DRVY
(derivada na direção y), para obter as componentes Uzz, Uxz, e Uyz. Aplicou-se também o
filtro INTG (Integral vertical), sendo obtido o Potencial Gravitacional. A partir deste foram
aplicados os filtros de derivada segunda DRVY e DRVX para obter as componentes Uyy
e Uxx respectivamente. Outrossim, sobre o Potencial Gravitacional foi aplicado o filtro de
derivada primeira DRVX para obter a componente Ux, e a partir desta foi aplicado o filtro
de derivada primeira DRVY, gerando a componente Uxy.
Infelizmente, a filtragem introduziu ruídos nas anomalias de alta frequência dos grids
resultantes. Foi observado um fenômeno conhecido com “ringing”, que gera falsas
ondulações. Fez-se necessária a aplicação posterior de novo filtro, no caso, o filtro BTWR
66
(Filtro Butterworth). O filtro Butterworth pode funcionar com um filtro passa-baixas ou
passa-altas dependendo dos parâmetros utilizados. No caso, o filtro foi aplicado como um
passa-baixas, com os seguintes parâmetros: comprimento de onda central = 800 Hz e grau
da função = 8.
O resposta ao modelo da solução analítica proposta também foi transportada para o
Oasis Montaj. Foram gerados mapas, cujos resultados encontram-se nas figuras de 15 a 26.
Onde deve-se considerar que 1 mGal/km = 10 Eötvös.
Figura 15 – Solução analítica,componente Uxx.
67
Figura 16 – Filtragem no Oasis Montaj/MAGMAP, componente: Uxx
68
Figura 17 – Solução analítica, componente: Uyy
69
Figura 18 – Filtragem no Oasis Montaj/MAGMAP, componente: Uyy
70
Figura 19 – Solução analítica, componente: Uzz
71
Figura 20 – Filtragem no Oasis Montaj/MAGMAP, componente: Uzz
72
Figura 21 – Solução analítica, componente: Uxy
73
Figura 22 – Filtragem no Oasis Montaj/MAGMAP, componente: Uxy
74
Figura 23 – Solução analítica, componente: Uxz
75
Figura 24 – Filtragem no Oasis Montaj/MAGMAP, componente: Uxz
76
Figura 25 – Solução analítica, componente: Uyz
77
Figura 26 – Filtragem no Oasis Montaj/MAGMAP, componente: Uyz
Observa-se o mesmo padrão nas anomalias, embora ocorra uma variação nos valores.
As variações são relacionadas aos métodos adotados: atribuição de valores nas equações
(solução proposta) e transformadas de Fourier n o Oasis Montaj/MAGMAP. Com isso, a
solução analítica se considera mais precisa, pois os valores obtidos nas transformadas de
Fourier são oriundos de aproximações.
5.5 AVALIAÇÃO COMPORTAMENTAL DA FUNÇÃO CONTRASTE DE
DENSIDADE
A função contraste de densidade, representada pela equação 2, apresenta um termo
independente, p. Algebricamente, o termo independente é somado à densidade média da
78
rocha encaixante fazendo-o responsável pela transformação de uma função densidade
numa função contraste de densidade.
Considere o perfil A-A' da figura 7, simulações feitas com o termo independente, p, da
equação 2, atribuindo diferentes valores a este termo e mantendo para os demais termos os
valores: q=203,435, r=-26,764 e s=1,4247 mostraram que na medida em que os valores
se tornam maiores, o comportamento da função mudou. A função apresentou dois tipos de
pontos de inflexão: o primeiro registrou uma mudança mais abrupta do gradiente vertical
(Uzz) e o segundo uma mais suave. Os pontos de inflexão do primeiro tipo (mostrados por
círculos azuis na figura 27) se referem aos limites do corpo. Os pontos de inflexão do
segundo tipo (mostrados por círculos pretos na figura 27) são resultante da soma dos
termos linear, quadrático e cubico da função e geram um abaulamento no centro da curva.
Observou-se nos casos onde o termo independente, p, assumiu valores positivos que
os pontos de inflexão do primeiro tipo se situaram próximos à base da anomalia, retratando
uma situação onde uma estrutura geológica mais densa sobrepõem uma estrutura menos
densa. Por outro lado, quando o termo independente, p, assumiu valores negativos, os
pontos de inflexão do primeiro se situaram próximos à borda da anomalia, retratando uma
situação onde estruturas geológicas menos densa sobrepõem estruturas mais densas, tal
como numa bacia sedimentar.
79
Figura 27 – Simulações com o termo independente da função polinomial cúbica.
80
6 APLICAÇÃO DAS EQUAÇÕES DA COMPONENTE TENSORIAL VERTICAL
NA BACIA POTIGUAR
Figura 28 – A Bacia Potiguar
Fonte: www.bdep.gov.br (26/05/2012, 18:04)
Formada a partir do fraturamento da Gondwana, a Bacia Potiguar, representada pela
elipse vermelha da figura 28, se situa no nordeste do Brasil, precisamente nos estados do
Ceará e Rio Grande do Norte. Limita-se ao sul, leste e oeste com rochas do embasamento
cristalino, ao norte com o oceano Atlântico e a noroeste com a Bacia do Ceará.
Segundo Araripe & Feijó (1994) da base ao topo o pacote sedimentar da Bacia
Potiguar está dividido em três grandes grupos:
• Grupo Areia Branca, composto pelas formações: Pendência, Pescada e Alagamar;
• Grupo Apodi, composto pelas formações: Açu, Ponta do Mel, Jandaíra e
Quebradas;
• Grupo Agulha, composto das formações: Ubarama, Guamaré, Tibau e Barreiras.
Segundo alguns autores, as formações descritas nos grupos acima teriam a seguinte
geocronologia e composição de rochas:
• Formação Pendência – Originada no Cretáceo, de acordo com SOUZA (1982) é
composta de arenito, siltito e folhelho.
81
• Formação Pescada – Datada do Cretáceo Inferior, é composta por arenitos médios,
com intercalação de folhelhos e siltitos.
• Formação Alagamar – Datada do Cretáceo Inferior, de acordo com SOUZA (1982)
é composta por: Membro Upanema (arenito fino e grosso e folhelho), Camada
Ponta do Tubarão (folhelho, calcilutitos e calcarenitos) e Membro Galinhos (pelito,
folhelho e calcilutito).
• Formação Açu –
Originada no Cretáceo, de acordo com KEGEL (1957a) a
formação pode ser subdividida em uma seção inferior de arenitos grosseiros, uma
média de arenitos finos e argilosos e uma superior de arenitos calcíferos.
• Formação Ponta do Mel – Datada do Cretáceo, de acordo com SOUZA (1982) é
formada por calcarenito oncolítico e doloespatito sobreposto por arenito fino a
médio. Havendo uma seção de calcilutito a plutônicos intercalados com folhelho.
• Formação Quebradas – Datada do Cretáceo, segundo SOUZA (1982) é constituída
por folhelhos e arenito fino a médio.
• Formação Jandaíra – Datada do Cretáceo, segundo SAMPAIO (1968) é constituída
de carbonatos marinhos de águas agitadas.
• Formação Ubarama – Datada do Cretáceo Superior, segundo SOUZA (1982) é
constituída de folhelhos, argilitos, arenitos grossos a muito finos, siltitos e
calcarenitos finos.
• Formação Guamaré – Datada do Terciário, segundo SOUZA (1982) é constituída
de calcarenito, calcilutito, folhelho e arenito.
• Formação Tibau – Datada do Terciário, segundo CAMPOS (1968) é constituída de
arenito fino.
82
• Formação Barreiras – Datada do Plio-Pleistoceno, recobre as formações anteriores
com argilitos e arenitos conglomeraticios.
Para o presente estudo, foi selecionada uma região entre as seguinte coordenadas do
sistema SAD-69/Brazil Polyconic:
Minimo
Máximo
Longitude
-37,4900º
-37,3880º
Latitude
-5,3629º
-5,2992º
X
6829800
6840800
Y
9382091
9389591
Tabela 1 – coordenadas da região estudada
A região se encontra no estado do Rio Grande do Norte, nos municípios de
Governador Dix-Sept Rosado e Mossoró, correspondendo ao retângulo vermelho da figura
29.
Na
região,
se
encontra
parte
do
levantamento
gravimétrico
terrestre,
DEBARDENEST, no qual foi selecionado para aplicação do modelo a região
correspondente às coordenadas descritas acima. A figura 30 representa a anomalia Bouguer
nestas coordenadas do levantamento DEBARDENEST.
83
Figura 29 – Mapa político da região com localização dos poços e a área selecionada .
84
Figura 30 – Carta da Anomalia Bouguer da região selecionada
Complementando as informações obtidas com os dados de métodos potenciais, foram
selecionados 10 poços, próximos a região, cuja perfilagem atingisse o embasamento.
85
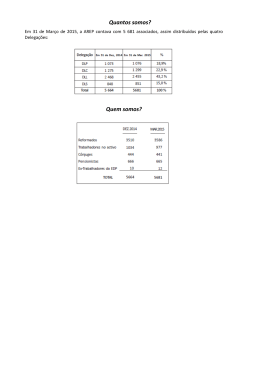
A profundidade do topo de cada uma das formações da bacia Potiguar, de acordo com
a perfilagem dos poços, encontram-se na tabela 2, em metros (m):
Poço
LAT
LONG
Jandaíra
Açu
Alagamar Pendência
Embasamento
1-BRSA-195-RN
-5,3142 -37,4333
5,00
289,00
795,00
990,00
1.313,00
1-BRSA-680-RN
-5,2147 -37,2941
7,00
303,00
797,00
975,00
2.080,00
1CD 0002 RN
-5,2949 -37,4510
4,50
257,00
745,00
-
773,00
1DR 0003 RN
-5,4885 -37,5707
5,00
137,00
534,00
672,00
817,00
1DR 0006 RN
-5,5094 -37,5423
5,00
127,00
507,00
629,00
1.675,00
1LOR 0001 RN
-5,5106 -37,4859
27,00
193,00
558,00
700,00
3.089,00
1RT 0001 RN
-5,4308 -37,5299
5,00
244,00
683,00
852,00
2.517,00
4LOR 0002 RN
-5,3196 -37,4792
5,00
152,00
515,00
621,00
3.380,00
1RMO 0001 RN
-5,3338 -37,4507
5,00
321,00
833,00
1.033,00
1.863,00
1 LB 0001 RN
-5,3688 -37,3846
5,50
293,00
770,00
957,00
2.012,00
Tabela 2 – Poços selecionados e profundidade das formações
Objetivando-se aplicar a solução analítica proposta na região, foi necessário inferir a
profundidade do embasamento e calcular uma função contraste de densidade. Estes serão
os tópicos abordados nas seções seguintes.
86
6.1 DETERMINAÇÃO DE UMA FUNÇÃO CONTRASTE DE DENSIDADE PARA
A REGIÃO
Conforme Zhang et al. (2001), o contraste de densidade no ponto P (x,z) de um corpo
3-D pode ser representado por:
Nx
(191)
Nz
i
j
 x , z =∑ ∑ a ij x z , comi=1,... , N x e j=1,... , N z
i=0 j=0
com i=0,1, …, Nx
e j=0,1, …, Nz,
onde a ij x i z j , os coeficiente do polinômio, são constante que podem ser estimadas através
dos mínimos quadrados utilizando observações conhecidas. Os valores de Nx e Nz são as
potencias máximas de x e z.
Fazendo Nx=0 e Nz=3, a equação 191 seria representada por:
3
(192)
 z=∑ a 0j z , com j=0,1,2,3
j
j=0
Considerando que: a 00= p ; a01=q ; a02 =r ; e a 03=s. , a equação 192 resultaria na
equação 2.
A partir dos perfis de poços descritos na seção 5.2, foram obtidas 61.682 observações
de densidade (ρ) das rochas da subsuperfície ate o embasamento, a partir dos perfis RHOB
dos 10 poços relacionados na seção anterior.
87
Objetiva-se representar a densidade da região interna à área de interesse apresentada
na figura 29, através do ajustamento de uma curva, que represente uma relação funcional
entre os valores observados. A relação funcional em questão é a função polinomial cúbica
de contraste de densidade, Δρ(z), representada nas equações 2 e 192, para obtê-la se faz
necessário inferir os coeficientes.
Busca-se que os valores de densidade observados, yo, estejam o mais próximo
possível da curva de ajuste inferida, yc. Havendo desta forma, um mínimo resíduo, δ = yc
– yo.
Baseado nisto, a formulação do problema pode ser representada da seguinte forma:
(193)
min pt p
sujeito a : A p− yot  A p− yo=
Onde :
δ =erro medio quadrático ;
A=matriz dos coeficientes da função;
yo=densidade observada nos poços ;
p=vetor dos coeficientes da função polinomial cúbica.
A matriz A e os vetores p e yo possuem as seguintes representações:
 

yo1
p
1 z 1 z 21 z 31
p= q ; A= ⋮ ⋮ ⋮ ⋮ ; e yo= yo2
r
⋮
1 z n z 2n z 3n
s
yon

Com isto, os valores de p podem ser obtidos através da resolução da seguinte
equação matricial:
p= At A−1 At yo
88
(194)
Assim,
foi inferida a curva de ajuste da equação 195, que representa a função
densidade, ρ(z), para a região. Nela a profundidade, z, se encontra em quilômetros, km.
(195)
 z=2189,5−158,02 z 64,35 z 2−27,55 z 3 kg /m³ 
Consequentemente, considerando a densidade média de embasamento de 2670 kg/m³
foi a função contraste de densidade, Δρ(z), representada pela equação 196.
  z =−477,51−158,02 z64,35 z 2−27,55 z 3  kg / m³ 
(196)
As curvas da figura 31 representam graficamente as equação 196 e 195
respectivamente. Nota-se que a função contraste de densidade, Δρ(z), é decrescente,
enquanto a função densidade, ρ(z), é crescente.
a
3
∆ ρ (z) k g/m
-5 0 0
-4 0 0
-3 0 0
-2 0 0
-1 0 0
0
0 .5
1
1 .5
P r o fu n d i d a d e (k m )
b
2
2 .5
0
0 .5
1
1 .5
P r o fu n d i d a d e (k m )
2
2 .5
3
ρ (z ) k g/m
2600
2500
2400
2300
2200
Figura 31 – Comportamento das funções contraste de densidade (a) e densidade (b)
A figura 32 representa a nuvem de valores de densidade observados nos poços e a
curva inferida da função densidade, ρ(z). Observa-se que, apesar de haver uma grande
dispersão nos pontos, a curva de ajuste inferida representa, dentro de um certo intervalo, a
tendencia de variação da densidade, seguindo a tendencia da maior população de pontos.
89
2700
2600
2500
2400
2300
2200
2100
2000
1900
0
0 .5
1
1 .5
2
2 .5
3
3 .5
4
4 .5
Figura 32 – Nuvem de pontos observados e curva ajustada.
6. 2 MODELO DO EMBASAMENTO APROXIMADO PARA A REGIÃO
Objetivando-se determinar a topografia da interface entre o embasamento e o pacote
sedimentar,
com
base
nos
valores
de
anomalia
Bouguer
do
levantamento
DEBARDENEST, foram utilizadas 408 observações, situadas 15 cm acima do solo.
Admitimos que o espaço ocupado pelo pacote sedimentar fosse dividido em 368 prismas
adjacentes, com densidade variando com a profundidade (z) e dimensões horizontais (x e
y) constantes de 500m. O topo de cada prisma também é constante (profundidade igual a
zero), porém a base irá variar de acordo com a topografia do embasamento. Desta forma,
temos um problema cujos parâmetros são as profundidades dos 368 prismas.
De acordo com Blakely (1996, p. 216) estamos diante de um problema de inversão
não-linear. Uma das formas de se obter a resolução do problema descrito acima é através
do método do Gradiente Aceitável. No caso, pode-se utilizar o sub-método de Levenberg90
Marquardt que garante a convergência para o mínimo da função. Com isso, a solução do
problema pode ser obtida iterativamente através da equação 197.
t
t
p k 1= p k  J J  I  J  g , com k =1,... , n
(197)
onde n é o total de iterações, I é matriz identidade e λ é o parâmetro de Marquardt. A
variável Δg corresponde à resposta do modelo aos dados ajustados, e sua representação é a
seguinte:
 g= g obs −g calc
(198)
Quanto a J representa uma matriz jacobiana cujos elementos são:
∂g
J ij= i , comi=1,. . , N e j=1,... , M
∂ pj
(199)
p j são os elementos do vetor profundidade P (da base ao topo de cada prisma), g i são os
elementos do vetor de resposta do modelo, M é o número de prismas e N é o número de
observações. O cálculo da matriz Jacobiana equação 199, pode ser efetuado através de
derivação numérica, conforme a equação 200. A cada profundidade de prisma seria
atribuída uma pequena perturbação (perturb), calculando-se a resposta ao modelo.
f  x perturb− f x
f '  x=
perturb
(200)
O teste de convergência pode ser feito através da raiz media quadrática, conforme
equação 201.
91
∑
(201)
N
RMQ=
i=1
2
g obs −g calc 
N
onde N é o numero de observações.
Utilizando-se um valor inicial para o parâmetro de Marquardt de 10−6 , a convergência
foi atingida após 129 iterações, realizadas em 6 min 47 s, em um Notebook HP Pavilion
DV7-4069, com processador AMD Phenom II Triple-Core, 2.1 GHz e 4096 GB de
memoria RAM, onde foi efetuando teste de convergência de 1 mGal.
A figura 33 apresenta o modelo de embasamento resultante do método empregado. A
profundidade encontra-se em metros.
Na figura 34, está representado o Mapa de Contorno do embasamento inferido para a
região. As cores variam gradativamente do vermelho ao azul mais intenso, representando
as estruturas . As mais rasas estão na cor vermelha e as mais profundas na cor azul. Cabe
informar ainda que os dados estão representados no sistema de coordenadas métricas
SAD/69 Brazil Polyconic.
92
0
P ro fu n d id a d e (m )
500
1000
1500
2000
2500
3000
9385091
6840800
6838600
9383591
6836400
6834200
9382091
N o rte (m )
6832000
6829800
L e s te (m )
Figura 33 – Embasamento inferido para a região. Azimute: -40º e Elevação: 32º
93
Figura 34 – Mapa de contorno do embasamento inferido
94
6.3 APLICAÇÃO DO MODELO DIRETO AO EMBASAMENTO INFERIDO
Considere que o pacote sedimentar seja dividido em 368 prismas justapostos com
arestas de 500 metros nas direções horizontais (x e y). Assumindo-se que cada prisma
localiza-se 15 cm abaixo dos pontos de observação (estações), e que o espaçamento das
estações é de 500 m. Assumindo-se também que o contraste de densidade da região é
representado pela equação 196. Com base neste modelo prismático, a anomalia
gravimétrica calculada através das equações 141, 146, 151 e 156 é representada pela figura
35. Observa-se nesta figura um gradiente na direção Noroeste-Sudeste. O baixo
gravimétrico localizado no Sudeste representa parte do graben Boa Vista e o alto, situado
no Noroeste, parte de um “host” que limita lateralmente aquele graben.
Tomando como base a anomalia Bouguer apresentada na figura 30, aplicando-se ao
“grid” o filtro de primeira derivada DRVZ (derivada na direção z) da extensão MAGMAP
do Oasis Montaj foi obtido o mapa da figura 36. O método destacou os contatos das
estruturas. Contudo, também há perda dos detalhes das estruturas.
Considerando que 1 Eötvös = 10−4 mGal/m, foi efetuada a carta de diferenças da
figura 37.
95
Figura 35 – Componente Uzz do embasamento inferido para a região.
96
Figura 36 – Carta da primeira derivada vertical para a região.
97
Figura 37 – Carta de diferenças das componentes Uzz .
98
6.4 DETERMINAÇÃO DO CONTRASTE DE DENSIDADE CONSTANTE
De acordo com Litinsky (1989), numa bacia sedimentar com n camadas sedimentares
de diferentes espessuras h e contrastes de densidade   , a densidade media ponderada
dos sedimentos   por ser calculada através da seguinte equação:
(202)
n
  hi
 =∑
, i=1,. .. , n
i=1 hi
Considerando a densidade media do embasamento de 2670 kg/m³, as informações de
perfilagem de poços contidas na tabela 2 (onde se pode obter uma espessura media para
cada uma das camadas) e as densidades observadas nos poços a partir do perfil RHO, foi
compilada a tabela 3.
Formação
h_media(m)
Δρ_medio( kg/m³)
Jandaíra
231,60
-158,06
-36607,29
Acu
442,10
-415,54
-183709,04
Alagamar
143,70
-404,66
-58149,46
Pendencia
1134,50
-234,85
-266440,21
-
1951,90
-
Δρ x h (kg/m³ x m)
-544905,99
Tabela 3 – Contraste de densidade médio na região estudada
A partir dos totais da tabela 3 e da equação 202, o cálculo da densidade media
ponderada dos sedimentos,   , resultou em de -279,17 kg/m³. Por fim, o modelo
prismático foi testado com a densidade media ponderada resultando no mapa da figura 38.
99
Nota-se uma piora na resolução, ocorrendo perda nos detalhes das estruturas mais
profundas.
Figura 38 – Mapa da componente Uzz com densidade constante.
100
7 CONCLUSÕES
Uma solução analítica para o cálculo da componentes gravimétricas tensoriais com a
densidade variando com a profundidade de acordo com uma função polinomial cúbica foi
apresentada.
A solução analítica foi validada matematicamente considerando que o Tensor
Gradiente é uma matriz simétrica cuja diagonal principal obedece à equação de Laplace.
Outrossim, foram positivos os testes comparativos da solução analítica com uma solução
numérica. Além de estudos comparativos com os resultados obtidos em um software já
estabelecido no mercado.
A solução analítica proposta foi aplicada numa região da bacia Potiguar, para onde foi
apresentada uma função polinomial cúbica de contraste de densidade. Para a região, a
utilização de uma função polinomial cubica apresentou uma melhor resolução das
estruturas geológicas mais profundas do que a utilização de densidade constante.
Além das 24 equações da solução analítica, também foram apresentadas 6 equações
baseadas no trabalho de Nagy et. al. (2000), que, semelhante ao estudo de GarciaAbdeslem (1992), podem ser utilizadas tanto na resolução de problemas diretos quanto
inversos de gradiometria gravimétrica com função de densidade variável.
Matematicamente, a anomalia gravimétrica é inversamente proporcional ao cubo da
distancia. Logo, ela é mais sensível a corpos mais rasos. Por sua vez, a gradiometria
mostrou-se mais sensível ainda, pois é inversamente proporcional à quinta potencia da
distancia. O uso de uma função polinomial cúbica demonstrou atenuar este fenômeno,
notou-se um maior detalhamento das estruturas quando foi utilizada uma função
101
polinomial cúbica, ao invés de densidade constante. Os estudos efetuados demostraram
grande influencia da função contraste de densidade, tanto no modelo inverso quanto no
modelo direto. Recomenda-se que na confecção de uma função contraste de densidade seja
utilizado o maior adensamento possível de poços. Além disso, os poços devem atingir o
embasamento e possuírem informações de todas as camadas sedimentares conhecidas na
área de estudo. Finalmente, deve-se considerar que a presença de hidrocarbonetos diminui
os valores da função contraste de densidade.
102
8 REFERÊNCIAS BIBLIOGRÁFICAS
ARARIPE, P. T.; FEIJÓ, F.J., Bacia Potiguar. Boletim de Geociências da Petrobras. Rio de
Janeiro, v. 8, n. 1, p. 127-141, 1994 .
ATHY, L. F. Density, porosity and compaction of sedimentary rocks. American
Association Petroleum Geology Bulletin. v. 14, n. 1, p. 1-24. 1930.
BANERJEE, B., GUPTA, S. P. D. Gupta, Gravitational attraction of a rectangular
parallelepiped. Geophysics, v. 42, n. 5, p. 1053-1055, aug. 1977.
BEURLEN, K. Geologia da região de Mossoró. Rio de Janeiro, Pongeti,(Coleção
Mossoroense, Série C, 18). p. 215.1967.
BASKARA RAO, D.Modelling of Sedimentary Basins from Gravity Anomalies with
Variable Density Constrat, Geophysical. J. Roy. Astr. Soc. n. 3, p. 63-67. 1986.
BLAKELY, R. J., The Potential Theory in Gravity and Magnetic Applications. Cambridge,
United Kingdon: Cambridge University Press. 1996. 464 p.
BRAGA, M. A., Modelagem Numérica e Validação de Dados Tensoriais da
Aerogradiometria Gravimétrica 3D-FTG. 2006. 77 f. Dissertação (Mestrado em
Geologia) - Instituto de Geociencias – UFRJ, Rio de Janeiro, 2006.
CAMPOS E SILVA, A. Considerações sobre o Quaternário do Rio Grande do Norte. Arq.
Inst. Antropol. UFRN, Natal, v. 2 (½). p. 275-301, 1966.
CHAI, Y.; HINZIE., W. J. Gravity inversion of an interface above which the density
contrast varies exponentially with depth. Geophysics, v. 53, p. 837-845. 1988.
CORDELL, L. Gravity analysis using an exponential density-depth function – San Jacinto
graben, California. Geophysics. v. 38, p. 684-690. 1973.
FREITAS, L. S.; CALÇA, J. A., Estatística: Teoria e exercícios de aplicação. São
Bernardo do Campo: Universidade Metodista de São Paulo, p. 145. 2007.
GALLARDO-DELGADO, L. A.; PEREZ-FLORES, M. A.; GOMEZ-TREVIÑO, E. A
versatile algorithm for joint a 3D inversion of gravity and magnetic data. Geophysics, v.
68, n. 3, p. 949-959. jun. 2003.
103
GARCIA-ABDESLEM, J. Gravitational attraction of a rectangular prism with depthdependent density. Geophysics, v. 57, n. 3, p. 470-473, mar. 1992.
GARCIA-ABDESLEM, J. The Gravitational attraction of a right rectangular prism with
density varying with depth following a cubic polynomial. Geophysics, v. 70, n. 6, p. J39J42, nov. 2005.
GARDSTEIN, I.S.; RYZHIK, I.M. Table of Integrals, Series, and Products. USA:
Academic Press Inc. 1980. 1160 p.
KEAREY, P., Geofísica de Exploração. Michael Brooks, Ian Hill; tradução Maria Cristina
Coelho. São Paulo: Oficina de Textos, p. 248 .2009.
LI, X. Vertical Resolution: Gravity versus vertical gradient. The Leading Edge, v. 20, p.
901-904, aug. 2001.
LITINSKY, V. A. Concept of effective density: Key to gravity depth determinations for
sedimentary basins. Geophysics, v. 54, n. 11, p. 1474-1482, nov. 1989.
MURPHY, C. A. The air-FTG airborne gravity gradiometer system. In: AIRBORNE
GRAVITY 2004 WORKSHOP, 18., 2004. Resumos...Camberra: ASEG-PESA, 2004. p.
7-14.
NAGY, D.; PAPP, G., BENEDEK J. The gravitational potential and its derivatives of the
prism: Journal of Geodesy, Germany, v. 74, p. 552-560, jun. 2000.
RAO, C. V.; CHAKRAVARTHI, C.; RAJU, M. L. Parabolic density function in
sedimentary basin modelling. PAGEOPH, v. 140, n. 3, p. 493-501. 1993.
SAMPAIO, A.V.; SCHALLER, H. Introdução à estratigrafia da bacia Potiguar. Boletim.
Técnico da Petrobras, Rio de Janeiro, v. 11, n. 1, p. 19-44. 1968.
SOUZA, S.M. de. Atualização da litoestratigrafia da Bacia Potiguar. In: CONGRESSO
BRASILEIRO DE GEOLOGIA, 32, Salvador, 1982. Anais do..., Salvador, SBG, v. 5, p.
2392-406. 1982.
ZHANG, C.; MUSHAYANDEBVU, M. F.; REID, A. B.; FAIRHEAD, J. D.; ODEGARD,
M. E. Euler deconvolution of gravity tensor gradient data. Geophysics, v. 66, n. 2, p. 512520 , mar. 2000.
ZHANG, J.; ZHONG., B.; ZHOU, X.; DAI., Y.Gravity anomalies of 2D bodies with
variable contrast. Geophysics, v. 66, n. 3, p. 809-813, may 2001.
104
9 APÊNDICES
APÊNDICE 1: PROGRAMA PARA CÁLCULO DAS COMPONENTES
TENSORIAIS
C*************************************************************
C
C CalcAnomalia - Calcula as componentes tensoriais da atracao
C
gravitacional provocada por um prisma
C
Regular Retangular com densidade variando com a
C
profundidade, com base no modelo de
C
Gracia-Abdeslem(2005).
C
C Americo dos Santos Jr.
C
C INPUT:
C
C NOBSX: Numero de observacoes na direcao x.
C NOBSY: Numero de observacoes na direcao y.
C z0 : Profundidade do prisma (km).
C P : Contraste de densidade observado na superficie (g/cm3).
C Q : Constante da funcao polinomial cubica (g/cm3/km).
C R : Constante da funcao polinomial cubica (g/cm3/km).
C S : Constante da funcao polinomial cubica (g/cm3/km).
C AX : Tamanho da aresta na direcao x (km).
C AY : Tamanho da aresta na direcao y (km).
C AZ : Tamanho da aresta na direcao z (km).
C CORDX: Coordenada inicial do prisma no eixo x.
C CORDY: Coordenada inicial do prisma no eixo y.
C CORDZ: Coordenada inicial do prisma no eixo z.
C
C OUTPUT:
C
C GG : Matriz com as componentes de gravidade (mGal) e as
C
componentes tensoriais (Eotvos)
C I : Coordenada em x da gravidade calculada.
C J : Coordenada em y da gravidade calculada.
C
C Rotinas chamadas:
C
C TzI1,TzI2,TzI3,TzI4,
C TxxI1,TxxI2,TxxI3,TxxI4,TxyI1,TxyI2,TxyI3,TxyI4,
C TxzI1,TxzI2,TxzI3,TxzI4,TyyI1,TyyI2,TyyI3,TyyI4,
C TyzI1,TyzI2,TyzI3,TyzI4,TzzI1,TzzI2,TzzI3 e TzzI4
105
C
C************************************************************
C
INTEGER*2 NOBSX,NOBSY,I,J,K,L,M,isign(2),Mi
REAL P,Q,RR,S,AX,AY,AZ,CORDX,CORDY,CORDZ,G,R
REAL x(2),y(2),z(2),x0,y0,z0
REAL GG(7,4)
REAL rho,rho1,rho2,rho3,rho4
REAL u,v,w,s2mg,km2m
data isign/-1,1/,Eo/1.e1/,rho/2670/,s2mg/1.e5/,km2m/1.e3/
C
G = 6.67e-11
OPEN(unit=01,file='PrismaGarcia.txt')
OPEN(unit=04,file='GzAmerico.txt')
OPEN(unit=05,file='GxxAmerico.txt')
OPEN(unit=06,file='GxyAmerico.txt')
OPEN(unit=07,file='GxzAmerico.txt')
OPEN(unit=08,file='GyyAmerico.txt')
OPEN(unit=09,file='GyzAmerico.txt')
OPEN(unit=10,file='GzzAmerico.txt')
READ(01,*)NOBSX
READ(01,*)NOBSY
READ(01,*)z0
READ(01,*)P
READ(01,*)Q
READ(01,*)RR
READ(01,*)S
READ(01,*)AX
READ(01,*)AY
READ(01,*)AZ
READ(01,*)CORDX
READ(01,*)CORDY
READ(01,*)CORDZ
C
P=0
C
Q=203.435
C
R=-26.764
C
R=1.4247
x(1)=CORDX
x(2)=CORDX+AX
y(1)=CORDY
y(2)=CORDY+AY
z(1)=CORDZ
z(2)=CORDZ+AZ
DO I=0,NOBSX
x0=I-0.5
DO J=0,NOBSY
y0=J-0.5
106
do ind1=1,7
do ind2=1,4
GG(ind1,ind2)=0.
end do
end do
DO K=1,2
u=x(K)-x0
DO L=1,2
v=y(L)-y0
DO M=1,2
w=z(M)-z0
R=SQRT(u**2+v**2+w**2)
rho1=P+Q*z0+RR*z0**2+S*z0**3
rho2=Q+2*RR*z0+3*S*z0**2
rho3=RR+3*S*z0
rho4=S
Mi = isign(K)*isign(L)*isign(M)
C
GG(1,1) =
GG(1,2) =
GG(1,3) =
GG(1,4) =
GG(1,1) + Mi*TzI1(rho1,u,v,w,R)
GG(1,2) + Mi*TzI2(rho2,u,v,w,R)
GG(1,3) + Mi*TzI3(rho3,u,v,w,R)
GG(1,4) + Mi*TzI4(rho4,u,v,w,R)
GG(2,1) =
GG(2,2) =
GG(2,3) =
GG(2,4) =
GG(2,1) + Mi*TxxI1(rho1,u,v,w,R)
GG(2,2) + Mi*TxxI2(rho2,u,v,w,R)
GG(2,3) + Mi*TxxI3(rho3,u,v,w,R)
GG(2,4) + Mi*TxxI4(rho4,u,v,w,R)
GG(3,1) =
GG(3,2) =
GG(3,3) =
GG(3,4) =
GG(3,1) + Mi*TxyI1(rho1,u,v,w,R)
GG(3,2) + Mi*TxyI2(rho2,u,v,w,R)
GG(3,3) + Mi*TxyI3(rho3,u,v,w,R)
GG(3,4) + Mi*TxyI4(rho4,u,v,w,R)
GG(4,1) =
GG(4,2) =
GG(4,3) =
GG(4,4) =
GG(4,1) + Mi*TxzI1(rho1,u,v,w,R)
GG(4,2) + Mi*TxzI2(rho2,u,v,w,R)
GG(4,3) + Mi*TxzI3(rho3,u,v,w,R)
GG(4,4) + Mi*TxzI4(rho4,u,v,w,R)
GG(5,1) =
GG(5,2) =
GG(5,3) =
GG(5,4) =
GG(5,1) + Mi*TyyI1(rho1,u,v,w,R)
GG(5,2) + Mi*TyyI2(rho2,u,v,w,R)
GG(5,3) + Mi*TyyI3(rho3,u,v,w,R)
GG(5,4) + Mi*TyyI4(rho4,u,v,w,R)
GG(6,1) =
GG(6,2) =
GG(6,3) =
GG(6,4) =
GG(6,1) + Mi*TyzI1(rho1,u,v,w,R)
GG(6,2) + Mi*TyzI2(rho2,u,v,w,R)
GG(6,3) + Mi*TyzI3(rho3,u,v,w,R)
GG(6,4) + Mi*TyzI4(rho4,u,v,w,R)
C
C
C
C
107
C
GG(7,1) = GG(7,1) + Mi*TzzI1(rho1,u,v,w,R)
GG(7,2) = GG(7,2) + Mi*TzzI2(rho2,u,v,w,R)
GG(7,3) = GG(7,3) + Mi*TzzI3(rho3,u,v,w,R)
GG(7,4) = GG(7,4) + Mi*TzzI4(rho4,u,v,w,R)
end do
end do
end do
WRITE(04,60)G*s2mg*km2m*(GG(1,1)+GG(1,2)+GG(1,3)+GG(1,4)),x0,y0
WRITE(05,60)G*s2mg*Eo*km2m*(GG(2,1)+GG(2,2)+GG(2,3)+GG(2,4)),x0,y0
WRITE(06,60)G*s2mg*Eo*km2m*(GG(3,1)+GG(3,2)+GG(3,3)+GG(3,4)),x0,y0
WRITE(07,60)G*s2mg*Eo*km2m*(GG(4,1)+GG(4,2)+GG(4,3)+GG(4,4)),x0,y0
WRITE(08,60)G*s2mg*Eo*km2m*(GG(5,1)+GG(5,2)+GG(5,3)+GG(5,4)),x0,y0
WRITE(09,60)G*s2mg*Eo*km2m*(GG(6,1)+GG(6,2)+GG(6,3)+GG(6,4)),x0,y0
WRITE(10,60)G*s2mg*Eo*km2m*(GG(7,1)+GG(7,2)+GG(7,3)+GG(7,4)),x0,y0
end do
end do
60 FORMAT(4X,G20.10,4X,G20.10,2X,G20.10)
CLOSE(01)
CLOSE(04)
CLOSE(05)
CLOSE(06)
CLOSE(07)
CLOSE(08)
CLOSE(09)
CLOSE(10)
STOP
END
C
C**********************************************************************
C
C TzI1 Calcula a componente vertical da anomalia para a primeira
C
parte da equacao de Garcia-Abdeslem
C
C**********************************************************************
C
REAL FUNCTION TzI1(rho1,u,v,w,R)
TzI1=rho1*(w*atan2(u*v,w*R)-u*alog(v+R)-v*alog(u+R))
RETURN
END
C**********************************************************************
C
C TzI2 Calcula a componente vertical da anomalia para a segunda
C
parte da equacao de Garcia-Abdeslem
C
C**********************************************************************
C
108
REAL FUNCTION TzI2(rho2,u,v,w,R)
real arg1,arg2,arg3,arg4
arg1=(1./2.)*(w**2)*atan2(u*v,w*R)
arg2=(1./2.)*(v**2)*atan2(w*u,v*R)
arg3=(1./2.)*(u**2)*atan2(w*v,u*R)
arg4=u*v*alog(w+R)
TzI2=rho2*(arg1-arg2-arg3+arg4)
RETURN
END
C**********************************************************************
C
C TzI3 Calcula a componente vertical da anomalia para a terceira
C
parte da equacao de Garcia-Abdeslem
C
C**********************************************************************
C
REAL FUNCTION TzI3(rho3,u,v,w,R)
real arg1,arg2,arg3,arg4
arg1=(1./3.)*(w**3)*atan2(u*v,w*R)
arg2=(1./3.)*(u**3)*alog(v+R)
arg3=(1./3.)*(v**3)*alog(u+R)
arg4=(2./3.)*u*v*R
TzI3=rho3*(arg1+arg2+arg3+arg4)
RETURN
END
C**********************************************************************
C
C TzI4 Calcula a componente vertical da anomalia para a quarta
C
parte da equacao de Garcia-Abdeslem
C
C**********************************************************************
C
REAL FUNCTION TzI4(rho4,u,v,w,R)
real arg1,arg2,arg3,arg4,arg5
arg1=(1./4.)*(u**4)*atan2(v*w,u*R)
arg2=(1./4.)*(v**4)*atan2(w*u,v*R)
arg3=(1./4.)*(w**4)*atan2(u*v,w*R)
arg4=(1./4.)*u*v*w*R
arg5=(1./2.)*u*v*(u**2+v**2)*alog(w+R)
TzI4=rho4*(arg1+arg2+arg3+arg4-arg5)
RETURN
END
C**********************************************************************
C
C TxxI1 Calcula a variacao do campo gravitacional no sentido
C
Leste-Oeste - primeira parte da solucao analitica proposta
C
109
C**********************************************************************
C
REAL FUNCTION TxxI1(rho1,u,v,w,R)
real arg1
arg1=atan2(v*w,u*R)
TxxI1=-1.*rho1*(arg1)
RETURN
END
C**********************************************************************
C
C TxxI2 Calcula a variacao do campo gravitacional no sentido
C
Leste-Oeste - segunda parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TxxI2(rho2,u,v,w,R)
real arg1
arg1=u*alog(v+R)
TxxI2=rho2*(arg1)
RETURN
END
C**********************************************************************
C
C TxxI3 Calcula a variacao do campo gravitacional no sentido
C
Leste-Oeste - terceira parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TxxI3(rho3,u,v,w,R)
real arg1,arg2
arg1=u*v*alog(w+R)
arg2=(u**2)*atan2(v*w,u*R)
TxxI3=-1.*rho3*(arg1-arg2)
RETURN
END
C**********************************************************************
C
C TxxI4 Calcula a variacao do campo gravitacional no sentido
C
Leste-Oeste - quarta parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TxxI4(rho4,u,v,w,R)
real arg1,arg2
arg1=(u**3)*alog(v+R)
arg2=u*v*R
TxxI4=-1.*rho4*(arg1+arg2)
110
RETURN
END
C**********************************************************************
C
C TxyI1 Calcula a anomalia associada aos "cantos" do prisma
C
primeira parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TxyI1(rho1,u,v,w,R)
real arg1
arg1=alog(w+R)
TxyI1=rho1*(arg1)
RETURN
END
C**********************************************************************
C
C TxyI2 Calcula a anomalia associada aos "cantos" do prisma
C
segunda parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TxyI2(rho2,u,v,w,R)
real arg1
arg1=R
TxyI2=rho2*(arg1)
RETURN
END
C**********************************************************************
C
C TxyI3 Calcula a anomalia associada aos "cantos" do prisma
C
terceira parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TxyI3(rho3,u,v,w,R)
real arg1,arg2,arg3
arg1=(1./2.)*w*R
arg2=(1./2.)*(u**2)*alog(w+R)
arg3=(1./2.)*(v**2)*alog(w+R)
TxyI3=rho3*(arg1-arg2-arg3)
RETURN
END
C**********************************************************************
C
C TxyI4 Calcula a anomalia associada aos "cantos" do prisma
C
quarta parte da solucao analitica proposta
111
C
C**********************************************************************
C
REAL FUNCTION TxyI4(rho4,u,v,w,R)
real arg1,arg2,arg3
arg1=(1./3.)*((w**2)-2.*(u**2)-2.*(v**2))*R
TxyI4=rho4*(arg1)
RETURN
END
C**********************************************************************
C
C TxzI1 Calcula o eixo de massa no sentido Norte-Sul da anomalia
C
primeira parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TxzI1(rho1,u,v,w,R)
real arg1
arg1=log(v+R)
TxzI1=rho1*(arg1)
RETURN
END
C**********************************************************************
C
C TxzI2 Calcula o eixo de massa no sentido Norte-Sul da anomalia
C
segunda parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TxzI2(rho2,u,v,w,R)
real arg1,arg2
arg1=v*alog(w+R)
arg2=u*atan2(v*w,u*R)
TxzI2=-1.*rho2*(arg1-arg2)
RETURN
END
C**********************************************************************
C
C TxzI3 Calcula o eixo de massa no sentido Norte-Sul da anomalia
C
terceira parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TxzI3(rho3,u,v,w,R)
real arg1,arg2
arg1=v*R
arg2=(u**2)*alog(v+R)
112
TxzI3=-1.*rho3*(arg1+arg2)
RETURN
END
C**********************************************************************
C
C TxzI4 Calcula o eixo de massa no sentido Norte-Sul da anomalia
C
quarta parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TxzI4(rho4,u,v,w,R)
real arg1,arg2,arg3,arg4
arg1=(u**3)*atan2(v*w,u*R)
arg2=(1./2.)*v*w*R
arg3=(1./2.)*(v**3)*alog(w+R)
arg4=(3./2.)*(u**2)*v*alog(w+R)
TxzI4=-1.*rho4*(arg1+arg2-arg3-arg4)
RETURN
END
C**********************************************************************
C
C TyyI1 Calcula a variacao do campo bgravitacional no sentido
C
Norte-Sul - primeira parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TyyI1(rho1,u,v,w,R)
real arg1
arg1=atan2(u*w,v*R)
TyyI1=-1.*rho1*(arg1)
RETURN
END
C**********************************************************************
C
C TyyI2 Calcula a variacao do campo bgravitacional no sentido
C
Norte-Sul - segunda parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TyyI2(rho2,u,v,w,R)
real arg1,arg2,arg3
arg1=v*alog(u+R)
TyyI2=rho2*(arg1)
RETURN
END
C**********************************************************************
C
113
C TyyI3 Calcula a variacao do campo bgravitacional no sentido
C
Norte-Sul - terceira parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TyyI3(rho3,u,v,w,R)
real arg1,arg2
arg1=v*u*alog(w+R)
arg2=(v**2)*atan2(w*u,v*R)
TyyI3=-1.*rho3*(arg1-arg2)
RETURN
END
C**********************************************************************
C
C TyyI4 Calcula a variacao do campo bgravitacional no sentido
C
Norte-Sul - quarta parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TyyI4(rho4,u,v,w,R)
real arg1,arg2
arg1=(v**3)*alog(u+R)
arg2=u*v*R
TyyI4=-1.*rho4*(arg1+arg2)
RETURN
END
C**********************************************************************
C
C TyzI1 Eixo de massa no sentido Leste-Oeste
C
primeira parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TyzI1(rho1,u,v,w,R)
real arg1
arg1=alog(u+R)
TyzI1=rho1*(arg1)
RETURN
END
C**********************************************************************
C
C TyzI2 Eixo de massa no sentido Leste-Oeste
C
segunda parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TyzI2(rho2,u,v,w,R)
114
real arg1,arg2,arg3,arg4
arg1=u*alog(w+R)
arg2=v*atan2(u*w,v*R)
TyzI2=-1.*rho2*(arg1-arg2)
RETURN
END
C**********************************************************************
C
C TyzI3 Eixo de massa no sentido Leste-Oeste
C
terceira parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TyzI3(rho3,u,v,w,R)
real arg1,arg2,arg3
arg1=u*R
arg2=(v**2)*alog(u+R)
TyzI3=-1.*rho3*(arg1+arg2)
RETURN
END
C**********************************************************************
C
C TyzI4 Eixo de massa no sentido Leste-Oeste
C
quarta parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TyzI4(rho4,u,v,w,R)
real arg1,arg2,arg3
arg1=(v**3)*atan2(u*w,v*R)
arg2=(1./2.)*u*w*R
arg3=(1./2.)*(u**3)*alog(w+R)
arg4=(3./2.)*u*(v**2)*alog(w+R)
TyzI4=-1.*rho4*(arg1+arg2-arg3-arg4)
RETURN
END
C**********************************************************************
C
C TzzI1 Calcula a componente vertical da anomalia
C
primeira parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TzzI1(rho1,u,v,w,R)
real arg1
arg1=atan2(u*v,w*R)
TzzI1=-1.*rho1*(arg1)
115
RETURN
END
C**********************************************************************
C
C TzzI2 Calcula a componente vertical da anomalia
C
segunda parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TzzI2(rho2,u,v,w,R)
real arg1,arg2
arg1=u*alog(v+R)
arg2=v*alog(u+R)
TzzI2=-1.*rho2*(arg1+arg2)
RETURN
END
C**********************************************************************
C
C TzzI3 Calcula a componente vertical da anomalia
C
terceira parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TzzI3(rho3,u,v,w,R)
real arg1,arg2,arg3
arg1=2.*u*v*alog(w+R)
arg3=(v**2)*atan2(u*w,v*R)
arg2=(u**2)*atan2(v*w,u*R)
TzzI3=rho3*(arg1-arg2-arg3)
RETURN
END
C**********************************************************************
C
C TzzI4 Calcula a componente vertical da anomalia
C
quarta parte da solucao analitica proposta
C
C**********************************************************************
C
REAL FUNCTION TzzI4(rho4,u,v,w,R)
real arg1,arg2,arg3
arg1=(u**3)*alog(v+R)
arg2=(v**3)*alog(u+R)
arg3=2.*u*v*R
TzzI4=rho4*(arg1+arg2+arg3)
RETURN
END
116
APÊNDICE 2: SCRIPT PARA GERAÇÃO DOS GRÁFICOS
%%Modelo de Zhang et al.
%%UFF - Universidade Federal Fluminense
%%Pos-graduacao em geologia e geofisica marinha
%%Orientador: Marco Polo Boanora
%%Aluno: Américo dos Santos Junior
%%Abril de 2011
%
clear;
% inicializa variaveis
%
% Le arquivo de parametros
%
fid = fopen('C:\Estudo\Tese\PrismaGarcia.txt','r');
ptx
= fscanf(fid, '%g',1);
% numero de pts de observacao x
pty
= fscanf(fid, '%g',1);
% numero de pts de observacao y
Z0
= fscanf(fid, '%g',1);
% elevacao da estacao
p
= fscanf(fid, '%g',1);
% observado na superficie (g/cm3)
q
= fscanf(fid, '%g',1);
% constante da funcao polinomial
r
= fscanf(fid, '%g',1);
% constante da funcao polinomial
s
= fscanf(fid, '%g',1);
% constante da funcao polinomial
Arestx= fscanf(fid, '%g',1);
% tam. das arestas x
Aresty= fscanf(fid, '%g',1);
% tam. das arestas y
Arestz= fscanf(fid, '%g',1);
% tam. das arestas z
Coordx= fscanf(fid, '%g',1);
% coordenadas dos prismas x
Coordy= fscanf(fid, '%g',1);
% coordenadas dos prismas y
Coordz= fscanf(fid, '%g',1);
% coordenadas dos prismas z
fclose(fid);
%
% "Plota" o Modelo
%
figure;
clf;
voxel([Coordx Coordy Coordz],[Arestx Aresty Arestz],'m',.2);
hold on;
for x=0.5:1:29.5
for y=0.5:1:29.5
plot(x,y,'.','lineWidth',1,'MarkerEdgeColor','g','MarkerFaceColor
','g','Markersize',8)
end
end
grid on;
xlabel('Leste (km)','FontSize',10,'fontweight','b');
ylabel('Norte (km)','FontSize',10,'fontweight','b');
%
% "Plota" os graficos do Modelo
%
Coordx=Coordx+0.5;
Coordy=Coordy+0.5;
figure;
load -ascii 'C:\Estudo\Tese\GzAmerico.txt'
for n=1:1:size(GzAmerico,1)
i=GzAmerico(n,2)+1.5;
j=GzAmerico(n,3)+1.5;
117
Tz(j,i)=round(GzAmerico(n,1));
end
%
[c,h]=contourf([0:1:30],[0:1:30],Tz);
clabel(c,h,'LabelSpacing',1152,'Color','k','FontWeight','bold','FontSize'
,9);
axis([0 30 0 30]);
ylabel('Norte (km)'),xlabel('Leste (km)');
title('Componente Uz')
h=colorbar('v');
set(get(h,'title'),'string','mGal');
hold on;
%
rectangle('Position',[Coordx
Coordy
Arestx
Aresty],'EdgeColor','k','lineWidth',1);
%
figure;
load -ascii 'C:\Estudo\Tese\GxxAmerico.txt'
for n=1:1:size(GxxAmerico,1)
i=GxxAmerico(n,2)+1.5;
j=GxxAmerico(n,3)+1.5;
Txx(j,i)=round(GxxAmerico(n,1));
end
%
[c,h]=contourf([0:1:30],[0:1:30],Txx);
clabel(c,h,'LabelSpacing',288,'Color','w','FontWeight','bold','FontSize',
10);
axis([0 30 0 30]);
ylabel('Norte (km)'),xlabel('Leste (km)');
title('(a)')
h=colorbar('v');
set(get(h,'title'),'string','Eötvös');
hold on;
rectangle('Position',[Coordx
Coordy
Arestx
Aresty],'EdgeColor','m','lineWidth',.5);
%
figure;
load -ascii 'C:\Estudo\Tese\GxyAmerico.txt'
for n=1:1:size(GxyAmerico,1)
i=GxyAmerico(n,2)+1.5;
j=GxyAmerico(n,3)+1.5;
Txy(j,i)=round(GxyAmerico(n,1));
end
%
[c,h]=contourf([0:1:30],[0:1:30],Txy);
clabel(c,h,'LabelSpacing',288,'Rotation',0,'Color','k','FontWeight','bold
','FontSize',10);
axis([0 30 0 30]);
ylabel('Norte (km)'),xlabel('Leste (km)');
title('(a)')
h=colorbar('v');
set(get(h,'title'),'string','Eötvös');
hold on;
rectangle('Position',[Coordx
Coordy
Arestx
Aresty],'EdgeColor','m','lineWidth',2);
%
figure;
118
load -ascii 'C:\Estudo\Tese\GxzAmerico.txt'
for n=1:1:size(GxzAmerico,1)
i=GxzAmerico(n,2)+1.5;
j=GxzAmerico(n,3)+1.5;
Txz(j,i)=round(GxzAmerico(n,1));
end
%
[c,h]=contourf([0:1:30],[0:1:30],Txz);
clabel(c,h,'LabelSpacing',288,'Rotation',0,'Color','k','FontWeight','bold
');
axis([0 30 0 30]);
ylabel('Norte (km)'),xlabel('Leste (km)');
title('(a)')
h=colorbar('v');
set(get(h,'title'),'string','Eötvös');
hold on;
rectangle('Position',[Coordx
Coordy
Arestx
Aresty],'EdgeColor','m','lineWidth',2);
%
load -ascii 'C:\Estudo\Tese\GyzAmerico.txt'
for n=1:1:size(GyzAmerico,1)
i=GyzAmerico(n,2)+1.5;
j=GyzAmerico(n,3)+1.5;
Tyz(j,i)=round(GyzAmerico(n,1));
end
%
figure;
[c,h]=contourf([0:1:30],[0:1:30],Tyz);
clabel(c,h,'LabelSpacing',288,'Rotation',0,'Color','k','FontWeight','bold
');
axis([0 30 0 30]);
ylabel('Norte (km)'),xlabel('Leste (km)');
title('(b)')
h=colorbar('v');
set(get(h,'title'),'string','Eötvös');
hold on;
rectangle('Position',[Coordx
Coordy
Arestx
Aresty],'EdgeColor','m','lineWidth',2);
%
figure;
load -ascii 'C:\Estudo\Tese\GyyAmerico.txt'
for n=1:1:size(GyyAmerico,1)
i=GyyAmerico(n,2)+1.5;
j=GyyAmerico(n,3)+1.5;
Tyy(j,i)=round(GyyAmerico(n,1));
end
%
[c,h]=contourf([0:1:30],[0:1:30],Tyy);
clabel(c,h,'LabelSpacing',288,'Color','w','FontWeight','bold','FontSize',
10);
axis([0 30 0 30]);
ylabel('Norte (km)'),xlabel('Leste (km)');
title('(b)')
119
h=colorbar('v');
set(get(h,'title'),'string','Eötvös');
hold on;
rectangle('Position',[Coordx
Coordy
Arestx
Aresty],'EdgeColor','m','lineWidth',.5);
%
figure;
load -ascii 'C:\Estudo\Tese\GzzAmerico.txt'
for n=1:1:size(GzzAmerico,1)
i=GzzAmerico(n,2)+1.5;
j=GzzAmerico(n,3)+1.5;
Tzz(j,i)=round(GzzAmerico(n,1));
end
%
[c,h]=contourf([0:1:30],[0:1:30],Tzz);
clabel(c,h,'LabelSpacing',576,'Color','w','FontWeight','bold','FontSize',
6);
axis([0 30 0 30]);
ylabel('Norte (km)'),xlabel('Leste (km)');
title('(b)')
h=colorbar('v');
set(get(h,'title'),'string','Eötvös');
hold on;
rectangle('Position',[Coordx
Coordy
Arestx
Aresty],'EdgeColor','k','lineWidth',.5);
120
APÊNDICE 3: SCRIPT PARA CÁLCULO DAS INTEGRAIS NUMERICAS
%%Integral numerica pela quadratura de Lobatto
%%UFF - Universidade Federal Fluminense
%%Pos-graduacao em geologia e geofisica marinha
%%Orientador: Marco Polo Boanora
%%Aluno: Américo dos Santos Junior
%%Fevereiro de 2012
%-----------------------------------------%Obtem os parametros do modelo
%-----------------------------------------fid = fopen('C:\Estudo\Tese\PrismaGarcia.txt','r');
ptx
= fscanf(fid, '%g',1);
% numero de pts de observacao x
pty
= fscanf(fid, '%g',1);
% numero de pts de observacao y
Ix
= fscanf(fid, '%g',1);
% intervalo de distancia eixo x
Iy
= fscanf(fid, '%g',1);
% intervalo de distancia eixo y
z0
= fscanf(fid, '%g',1);
% elevacao da estacao
p
= fscanf(fid, '%g',1);
% observado na superficie (g/cm3)
q
= fscanf(fid, '%g',1);
% constante da funcao polinomial
r
= fscanf(fid, '%g',1);
% constante da funcao polinomial
s
= fscanf(fid, '%g',1);
% constante da funcao polinomial
Qprisx= fscanf(fid, '%g',1);
% quantidade de prisma x
Qprisy= fscanf(fid, '%g',1);
% quantidade de prisma y
Qprisz= fscanf(fid, '%g',1);
% quantidade de prisma z
Arestx= fscanf(fid, '%g',1);
% tam. das arestas x
Aresty= fscanf(fid, '%g',1);
% tam. das arestas y
Arestz= fscanf(fid, '%g',1);
% tam. das arestas z
Coordx= fscanf(fid, '%g',1);
% coordenadas dos prismas x
Coordy= fscanf(fid, '%g',1);
% coordenadas dos prismas y
Coordz= fscanf(fid, '%g',1);
% coordenadas dos prismas z
fclose(fid);
%-----------------------------------------%Valores obtidos nas Integracoes Analiticas
%-----------------------------------------load -ascii 'C:\Estudo\Tese\GxxCalcAnomalia.txt'
load -ascii 'C:\Estudo\Tese\GxyCalcAnomalia.txt'
load -ascii 'C:\Estudo\Tese\GxzCalcAnomalia.txt'
load -ascii 'C:\Estudo\Tese\GyyCalcAnomalia.txt'
load -ascii 'C:\Estudo\Tese\GyzCalcAnomalia.txt'
load -ascii 'C:\Estudo\Tese\GzzCalcAnomalia.txt'
for n=1:1:size(GxxAmerico,1)
i=GxxAmerico(n,2);
j=GxxAmerico(n,3);
Txx1(j,i)=GxxAmerico(n,1);
Txy1(j,i)=GxyAmerico(n,1);
Txz1(j,i)=GxzAmerico(n,1);
Tyy1(j,i)=GyyAmerico(n,1);
Tyz1(j,i)=GyzAmerico(n,1);
Tzz1(j,i)=GzzAmerico(n,1);
end
%-----------------------------------------%Valores obtidos nas Integracoes Numericas
%-----------------------------------------%
121
G=6.67e-11;
% Constante gravitacional
universal
mGal=1e5;
% Conversao de m/s^2 para mGal
km2m=1.e3;
% Conversao de km para metros
Eo=1.e1;
% Conversao para Eotvos
isign=[-1;1];
x(1)=Coordx;
% Coordenada inicial do prisma em
x
x(2)=Coordx+Arestx;
% Coordenada final
do prisma em
x
y(1)=Coordy;
% Coordenada inicial do prisma em
y
y(2)=Coordy+Aresty;
% Coordenada final
do prisma em
y
z(1)=Coordz;
% Coordenada inicial do prisma em
z
z(2)=Coordz+Arestz;
% Coordenada final
do prisma em
z
w1=z(1)-z0;
w2=z(2)-z0;
for x1=1:Ix:ptx
x0=x1-0.9;
for y1=1:Iy:pty
Gz=0;
Gx=0;
Gy=0;
Gxy=0;
Gxx=0;
Gxz=0;
Gyy=0;
Gyz=0;
Gzz=0;
y0=y1-0.9;
for i=1:1:2
u=x(i)-x0;
for j=1:1:2
v=y(j)-y0;
Mi=isign(i)*isign(j);
fxx =['-(' num2str(p,'%.13f') '+' num2str(q,'%.13f')
'.*w'
num2str(r,'%.13f')
'.*w.^2+'
num2str(s,'%.13f')
'.*w.^3).*('
num2str(u,'%.13f') '.*' num2str(v,'%.13f') ')./((' num2str(u.^2,'%.13f')
'+w.^2).*('
num2str(u.^2,'%.13f')
'+'
num2str(v.^2,'%.13f')
'+w.^2).^0.5)'];
fxy =['(' num2str(p,'%.13f') '+' num2str(q,'%.13f') '.*w'
num2str(r,'%.13f')
'.*w.^2+'
num2str(s,'%.13f')
'.*w.^3).*(1/(('
num2str(u.^2,'%.13f') '+' num2str(v.^2,'%.13f') '+w.^2).^0.5))'];
fxz =['-(' num2str(p,'%.13f') '+' num2str(q,'%.13f')
'.*w'
num2str(r,'%.13f')
'.*w.^2+'
num2str(s,'%.13f')
'.*w.^3).*('
num2str(v,'%.13f')
'.*w)./(('
num2str(u.^2,'%.13f')
'+w.^2).*('
num2str(u.^2,'%.13f') '+' num2str(v.^2,'%.13f') '+w.^2).^0.5)'];
fyy =['-(' num2str(p,'%.13f') '+' num2str(q,'%.13f')
'.*w'
num2str(r,'%.13f')
'.*w.^2+'
num2str(s,'%.13f')
'.*w.^3).*('
num2str(u,'%.13f') '.*' num2str(v,'%.13f') ')./((' num2str(v.^2,'%.13f')
'+w.^2).*('
num2str(u.^2,'%.13f')
'+'
num2str(v.^2,'%.13f')
'+w.^2).^0.5)'];
fyz =['-(' num2str(p,'%.13f') '+' num2str(q,'%.13f')
'.*w'
num2str(r,'%.13f')
'.*w.^2+'
num2str(s,'%.13f')
'.*w.^3).*('
122
num2str(u,'%.13f')
'.*w)./(('
num2str(v.^2,'%.13f')
'+w.^2).*('
num2str(u.^2,'%.13f') '+' num2str(v.^2,'%.13f') '+w.^2).^0.5)'];
Gxy=Gxy+Mi*GaussLegendre(fxy,w1,w2,1024);
Gxx=Gxx+Mi*GaussLegendre(fxx,w1,w2,1024);
Gxz=Gxz+Mi*GaussLegendre(fxz,w1,w2,1024);
Gyy=Gyy+Mi*GaussLegendre(fyy,w1,w2,1024);
Gyz=Gyz+Mi*GaussLegendre(fyz,w1,w2,1024);
Gzz=GzzMi*(GaussLegendre(fxx,w1,w2,1024)+GaussLegendre(fyy,w1,w2,1024));
end
end
Txy2(y1,x1)=Eo*mGal*km2m*G*Gxy;
Txz2(y1,x1)=Eo*mGal*km2m*G*Gxz;
Txx2(y1,x1)=Eo*mGal*km2m*G*Gxx;
Tyy2(y1,x1)=Eo*mGal*km2m*G*Gyy;
Tyz2(y1,x1)=Eo*mGal*km2m*G*Gyz;
Tzz2(y1,x1)=Eo*mGal*km2m*G*Gzz;
end
end
%
figure;
xi=[1:1:30];
y=Txx1(15,:);
yi=Txx2(15,:);
plot(xi,y,'b-',xi,yi,'r o');
h = legend('Analitica','Numerica',-1);
set(gca,'XTick',[0:5:30])
set(h,'Interpreter','none')
ylabel('Gravity (Eötvös)'),xlabel('Leste (Km)');
title('Componente Uxx')
%
figure;
xi=[1:1:30];
y=Txy1(15,:);
yi=Txy2(15,:);
plot(xi,y,'b-',xi,yi,'r o');
h = legend('Analitica','Numerica',-1);
set(gca,'XTick',[0:5:30])
set(h,'Interpreter','none')
ylabel('Gravity (Eötvös)'),xlabel('Leste (Km)');
title('Componente Uxy')
%
figure;
xi=[1:1:30];
y=Txz1(15,:);
yi=Txz2(15,:);
plot(xi,y,'b-',xi,yi,'r o');
h = legend('Analitica','Numerica',-1);
set(gca,'XTick',[0:5:30])
set(h,'Interpreter','none')
ylabel('Gravity (Eötvös)'),xlabel('Leste (Km)');
title('Componente Uxz')
%
figure;
xi=[1:1:30];
y=Tyy1(15,:);
yi=Tyy2(15,:);
123
plot(xi,y,'b-',xi,yi,'r o');
h = legend('Analitica','Numerica',-1);
set(gca,'XTick',[0:5:30])
set(h,'Interpreter','none')
ylabel('Gravity (Eötvös)'),xlabel('Leste (Km)');
title('Componente Uyy')
%
figure;
xi=[1:1:30];
y=Tyz1(15,:);
yi=Tyz2(15,:);
plot(xi,y,'b-',xi,yi,'r o');
h = legend('Analitica','Numerica',-1);
set(gca,'XTick',[0:5:30])
set(h,'Interpreter','none')
ylabel('Gravity (Eötvös)'),xlabel('Leste (Km)');
title('Componente Uyz')
%
figure;
xi=[1:1:30];
y=Tzz1(15,:);
yi=Tzz2(15,:);
plot(xi,y,'b-',xi,yi,'r o');
h = legend('Analitica','Numerica',-1);
set(gca,'XTick',[0:5:30])
set(h,'Interpreter','none')
ylabel('Gravity (Eötvös)'),xlabel('Leste (Km)');
title('Componente Uzz')
124
APÊNDICE 4: ARQUIVO DE PARAMETROS DO PRISMA
Conteúdo do arquivo PrismaGarcia.txt:
30
30
-0.00015
-747.7
203.43
-26.764
1.4247
10.0
10.0
8.0
10.0
10.0
0.0
125