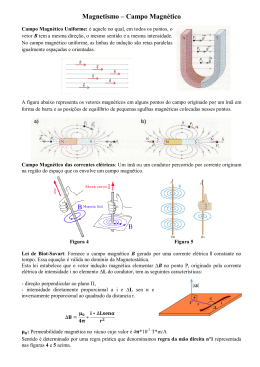
AULA 16.1
Conteúdo
Eletromagnetismo: Campo Magnético gerado por um fio e por um
solenoide.
Habilidades:
• Compreender os princípios físicos envolvidos no magnetismo e
eletromagnetismo para relacionar fenômenos e aplicações
práticas do cotidiano.
1
Verificamos experimentalmente que a intensidade (B) do campo
magnético criado por um fio reto e longo é proporcional à
intensidade de corrente elétrica (i) que o atravessa e é
inversamente proporcional à distância (r) do ponto até o fio:
𝝁𝟎 ∙ 𝒊
𝑩=
𝟐𝝅 ∙ 𝒓
2
Nessa expressão, a constante μ é a permeabilidade magnética do
meio em que está o fio. Para o vácuo, essa constante vale:
𝒎
−𝟕
𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙
𝑨
A unidade de medida para o campo magnético no Sistema
Internacional de Unidades (SI) é o tesla (T) em homenagem a
Nicola Tesla (1856-1943).
3
EXEMPLO
Um fio retilíneo e longo é percorrido por uma corrente elétrica
com intensidade de 10 A. Determine o módulo do vetor campo
magnético em um ponto P situado a 20 cm do fio. Considere que
o meio em que se encontra o fio é o vácuo.
4
EXEMPLO
Solução:
Dados:
i = 10 A
r = 20 cm = 0,2 m
−𝟕
𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙ 𝒎/𝑨
5
EXEMPLO
Solução:
Dados:
i = 10 A
r = 20 cm = 0,2 m
−𝟕
𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙ 𝒎/𝑨
𝝁𝟎 . 𝒊
𝑩=
𝟐𝝅. 𝒓
6
EXEMPLO
Solução:
Dados:
i = 10 A
r = 20 cm = 0,2 m
−𝟕
𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙ 𝒎/𝑨
𝝁𝟎 . 𝒊
𝑩=
𝟐𝝅. 𝒓
7
− 𝟕.
𝟏𝟎
𝟒π . 𝟏𝟎
𝑩=
𝟐π . 𝟎, 𝟐
EXEMPLO
Solução:
Dados:
i = 10 A
r = 20 cm = 0,2 m
−𝟕
𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙ 𝒎/𝑨
𝝁𝟎 . 𝒊
𝑩=
𝟐𝝅. 𝒓
8
− 𝟕.
𝟏𝟎
𝟒π . 𝟏𝟎
𝑩=
𝟐π . 𝟎, 𝟐
𝟒𝟎 . 𝟏𝟎
𝐁=
𝟎, 𝟒
−𝟕
EXEMPLO
Solução:
Dados:
i = 10 A
r = 20 cm = 0,2 m
−𝟕
𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙ 𝒎/𝑨
.
−𝟕
𝟏𝟎 𝟏𝟎
𝝁𝟎 . 𝒊
𝟒𝝅 ∙
𝑩=
∴ 𝑩=
𝟐𝝅 ∙ 𝒓
𝟐𝝅 ∙ 𝟎, 𝟐
∴
𝟒𝟎 ∙
𝐁=
𝟎, 𝟒
B = 400 . 10-6 T, em Not.Cient. B = 4,0 . 10-4 T
9
−𝟕
𝟏𝟎
SOLENOIDE
Um solenoide é constituído por um fio metálico enrolado no
formato de uma hélice cilíndrica. Ao ser atravessado por uma
corrente elétrica, cria um campo magnético cujas linhas são
mostradas na figura:
10
Solenoide
11
SOLENOIDE
Na física chamamos de solenoide todo fio condutor longo e
enrolado de forma que se pareça com um tubo formado por
espiras circulares igualmente espaçadas. Este condutor também
pode ser chamado de bobina chata. Portanto, ao se deparar com
ambos os nomes, lembre-se que eles são sinônimos, pois nos dois
casos temos um agrupamento de espiras.
12
SOLENOIDE
O enrolamento de um fio sobre um tubo de caneta, por exemplo,
é um solenoide. Configuramos um solenoide a partir da reunião
das configurações das linhas de campo magnético produzidas por
cada uma das espiras. Para fazermos um solenoide basta
enrolarmos um fio longo sobre um tubo de caneta, por exemplo.
A figura abaixo nos mostra um solenoide percorrido por uma
corrente elétrica i e de comprimento L.
13
Tubo de Ferro
14
SOLENOIDE
Como todo fio condutor percorrido por uma corrente elétrica gera
ao seu redor um campo magnético, não é diferente para um
solenoide. O campo magnético gerado em um solenoide possui as
seguintes características:
• No interior do solenoide consideramos o campo magnético
como sendo uniforme, portanto, as linhas de indução são
paralelas entre si.
• Quanto mais comprido for o solenoide, mais uniforme será o
campo magnético interno e mais fraco o campo magnético
externo.
15
SOLENOIDE
• Para o campo magnético uniforme no interior do solenoide
teremos um vetor indução em qualquer ponto interno do
solenoide, portanto, como se trata de um vetor, ele terá
intensidade, direção e sentido.
• O módulo, isto é, a intensidade do campo magnético no interior
de um solenoide é obtido através da seguinte equação:
𝑵
𝑩 = 𝝁 . .𝒊
𝑳
16
SOLENOIDE
𝑵
𝑩 = 𝝁 . .𝒊
𝑳
Onde: μ é a permeabilidade magnética do meio no interior do
solenoide e N/L representa o número de espiras por unidade de
comprimento do solenoide.
A direção do vetor indução magnética é retilínea e paralela ao
eixo do solenoide.
17
SOLENOIDE
𝑵
𝑩 = 𝝁 . .𝒊
𝑳
O sentido é obtido através da regra da mão direita.
Como existe um campo magnético no interior do solenoide,
podemos dizer que as extremidades de um solenoide são seus
polos.
18
SOLENOIDE
As aplicações práticas de um solenoide são inúmeras, dentre elas
podemos destacar:
• Válvula solenoide para vapor:
19
SOLENOIDE
• Válvula solenoide para a passagem de água ou ar:
20
SOLENOIDE
• Solenoide Rotativo (motor de arranque).
21
SOLENOIDE
• Eletroválvula
22
EXEMPLO
Um solenoide de 1 metro de comprimento contém 500 espiras e é
percorrido por uma corrente de 2A. Determinar a intensidade do
vetor campo magnético no interior do solenoide.
−𝟕
Adote 𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙ 𝒎/𝑨
23
EXEMPLO
Solução:
Dados:
L = 1,0 m
i=2A
24
N = 500 espiras
−𝟕
𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙ 𝒎/𝑨
EXEMPLO
Solução:
Dados:
L = 1,0 m
i=2A
N = 500 espiras
−𝟕
𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙ 𝒎/𝑨
𝒏
𝑩 = .𝝁 .𝒊
𝑳
25
EXEMPLO
Solução:
Dados:
L = 1,0 m
i=2A
N = 500 espiras
−𝟕
𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙ 𝒎/𝑨
𝒏
𝟓𝟎𝟎
−𝟕
𝑩 = .𝝁 .𝒊 ∴ 𝑩 =
. 𝟒 . 𝝅 . 𝟏𝟎 . 𝟐
𝑳
𝟏
𝑩 = 𝟒𝟎𝟎𝟎 . 𝟑, 𝟏𝟒
26
−𝟕
. 𝟏𝟎
EXEMPLO
Solução:
Dados:
L = 1,0 m
i=2A
N = 500 espiras
−𝟕
𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙ 𝒎/𝑨
𝒏
𝟓𝟎𝟎
−𝟕
𝑩 = .𝝁 .𝒊 ∴ 𝑩 =
. 𝟒 . 𝝅 . 𝟏𝟎 . 𝟐
𝑳
𝟏
𝑩 = 𝟒𝟎𝟎𝟎 . 𝟑, 𝟏𝟒
27
−𝟕
. 𝟏𝟎
∴ 𝑩 = 𝟏𝟐𝟓𝟔
−𝟕
. 𝟏𝟎
EXEMPLO
Solução:
Dados:
L = 1,0 m
i=2A
N = 500 espiras
−𝟕
𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙ 𝒎/𝑨
𝒏
𝟓𝟎𝟎
−𝟕
𝑩 = .𝝁 .𝒊 ∴ 𝑩 =
. 𝟒 . 𝝅 . 𝟏𝟎 . 𝟐
𝑳
𝟏
𝑩 = 𝟒𝟎𝟎𝟎 . 𝟑, 𝟏𝟒
−𝟕
. 𝟏𝟎
𝑩 = 𝟏, 𝟐𝟓𝟔
28
∴ 𝑩 = 𝟏𝟐𝟓𝟔
−𝟕
. 𝟏𝟎
𝑻
−𝟕
. 𝟏𝟎
DINÂMICA LOCAL INTERATIVA
1. Para a figura abaixo, determine o valor do vetor indução
magnética B situado no ponto P e marque a alternativa correta.
Adote 𝝁𝟎 = 4π x10-7T.m/A, para a permeabilidade magnética.
i = 20 A
5 cm
P
29
a) B = 4 . 10-5 T
-5
b) B = 8 . 10 T
-7
c) B = 4 . 10 T
d) B = 5 . 10-5 T
e) B = 8 . 10-7 T
DINÂMICA LOCAL INTERATIVA
2. Um solenoide de 50 cm de comprimento contém 2000 espiras e
é percorrido por uma corrente de 5A. Determinar a intensidade
do vetor campo magnético no interior do solenoide.
−𝟕
Adote 𝝁𝟎 = 𝟒𝝅 ∙ 𝟏𝟎 𝑻 ∙ 𝒎/𝑨
a) 1,25 x 10-2 T
b) 12,5 T
c) 25,512 T
d) 2,51 x 10-2 T
-7
e) 2,51 x 10 T
30