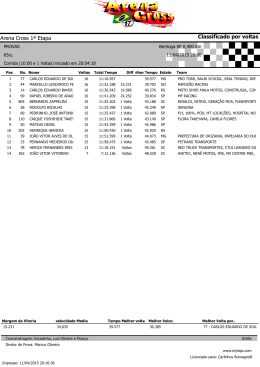
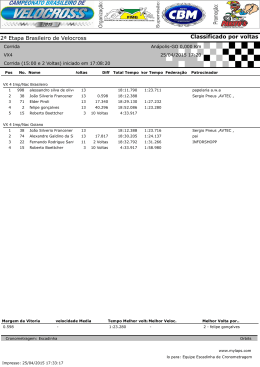
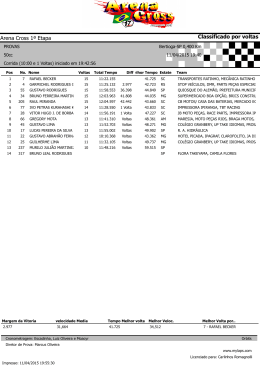
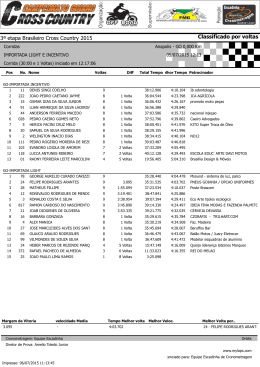
MATEMÁTICA
Prof. André Costa
1. Chamam-se frações unitárias as frações de numeradores iguais à unidade. Os antigos egípcios já
faziam uso de tais frações. Indique em qual das igualdades abaixo, não há uma decomposição
correta da fração dada em frações unitárias:
a)
b)
c)
d)
e)
2
1
1


15 10 30
2
1
1


15 12 20
2 1 1
 
5 3 15
2 1 1
 
7 4 28
2 1 1
 
13 8 52
2. Um dos problemas matemáticos mais antigos da humanidade data da época selêucida e afirma
que uma dada vara encontra-se encostada com uma das pontas em uma parede. Se essa vara
escorrega de modo que essa ponta arrie 3 unidades de comprimento, enquanto a extremidade
inferior da vara se afasta da parede 9 unidades de comprimento, quantas unidades de comprimento
tem a vara?
a) 12
b) 11
c) 15
d) 18
e) 13
3. Dado um segmento de comprimento L, o que é historicamente conhecido como secção áurea
deste segmento é a sua divisão em dois segmentos de comprimentos x e L - x , de modo que
L
x

x Lx
Com essa informação, é correto afirmar que:
x2  L  x
L( 5  1)
b) x 
2
2
2
c) x  x  L  L
a)
d) Se L é inteiro, então x é racional.
e)
x 2  x  L2  L
Humanas
1
4. Três números inteiros a, b e c são ditos pitagóricos, se a2 = b2 + c2. Se m é um inteiro positivo
ímpar qualquer, aponte em que alternativa abaixo há números pitagóricos.
m2  1
m2  1
,m,
2
2
2
2
b) m  1, m , m  1
a)
(m  1) 2 , m , (m  1) 2
m m m
, ,
d)
2 3 4
e) m  1, m , m  1
c)
5. Abaixo está descrito o chamado método das divisões sucessivas, ou método de Euclides para
determinação do MDC dos números 759 e 456.
1
456
153
759
303
1
303
150
1
153
3
1
150
0
50
3
O MDC entre 759 e 456 é 3, resultado da última divisão efetuada no processo (até obter-se resto
zero). Descubra o valor do número x nas divisões sucessivas abaixo.
x
80
2
150
70
1
80
10
1
70
0
7
10
a) x = 130
b) x = 230
c) x = 330
d) x = 380
e) x = 450
6. Diofante de Alexandria viveu por volta do 3º século A.C., sendo considerado o pai da Álgebra.
Dele é a solução de diversos problemas interessantes. Por exemplo, determinar dois números, cuja
soma seja 10 e a soma de seus cubos seja 370. Diante das opções abaixo, qual é o maior de tais
números?
a) 9,0
b) 8,4
c) 7,0
d) 6,7
e) 7,2
7. Dois polígonos são semelhantes e a razão de semelhança entre as medidas dos seus lados é 3/5.
Considere as afirmativas:
I - Se o perímetro do menor polígono é 60cm, então o maior polígono tem 100cm de
perímetro.
II – Os ângulos internos correspondentes estão na proporção de 3/5.
III - Se um ângulo do maior polígono mede 30º, então o ângulo correspondente no maior
polígono mede 50º.
Humanas
2
Nessas condições, é correto afirmar que:
a) apenas a afirmativa I é falsa.
b) as afirmativas I e III são verdadeiras.
c) apenas a afirmativa III é falsa.
d) todas as afirmativas são falsas.
e) apenas a afirmativa I é verdadeira.
8. Numa corrida de Fórmula 1, um piloto completa uma volta na pista do circuito a cada 1 minuto e
15 segundos. O total de voltas, em meia hora de corrida, se esse piloto não parar ou mudar o seu
ritmo de corrida, será aproximadamente:
a) 24 voltas
b) 25 voltas
c) 26 voltas
d) 28 voltas
e) 32 voltas
9. Em uma construção, um elevador de cargas tem capacidade máxima de 500 kg de carga.
Sabendo que será elevada uma tonelada e meia de tijolos para a parte superior da obra e, junto
com essa carga irão o operador do elevador e dois operários, perfazendo um total de 230 kg, e
sabendo, ainda, que o elevador subirá sempre com carga máxima, com exceção da última viagem,
quantos quilogramas de tijolos serão levados para a parte superior do prédio na última viagem?
a) 500
b) 450
c) 300
d) 200
e) 150
10. Numa pesquisa sobre as preferências por esportes entre os alunos do 4º período do Curso de
Saneamento do CEFET-PE, observou-se que 1/4 preferiam handebol, 1/6 futebol de salão, 2/9
futebol de campo, e o voleibol, o mais votado, obteve 13 votos. Sabendo que na turma há
exatamente 40 alunos, quantos NÃO participaram dessa pesquisa?
a) 0
b) 1
c) 2
d) 3
e) 4
11. O produto de dois números positivos é quarenta e cinco e a soma entre eles é catorze. A soma
dos inversos desses dois números é:
a)
b)
c)
d)
e)
1
14
2
14
1
45
2
45
14
45
Humanas
3
12. Um hexágono regular tem lados de medidas iguais a ℓ cm. Na figura abaixo, estão traçadas, em
linhas mais claras, as diagonais. Somando as medidas de todas as diagonais, tem-se:
a) 6(1 
b)
3)
3(1  2 3 )
c) (1
3)
d) 12
e)
6 3
13. Repartindo o número 72 em partes inversamente proporcionais a (3, 4, 6), obtém-se uma
seqüência, cujo maior termo é:
a) 16
b) 24
c) 32
d) 36
e) 48
14. Em uma confecção, 20 costureiras, em 8 dias, produzem 800 peças de roupas. Reduzindo para
16 o número de costureiras e aumentando o tempo para 12 dias, quantas peças de roupas serão
produzidas?
a) 760
b) 820
c) 860
d) 900
e) 960
15. A nova diretoria de uma associação de técnicos fez um levantamento e observou que, dentre
seus 5 000 sócios, 48% têm mais de 40 anos, 36% são pós-graduados e 1400 têm mais de 40 anos
e são pós-graduados. Considerando esses dados, é verdadeiro afirmar que o número de sócios com
até 40 anos sem pós-graduação é:
a) 400
b) 800
c) 1 200
d) 1 800
e) 2 200
Humanas
4
16. No pentágono regular abaixo qual a medida do ângulo NBQ?
a) 36º
b) 32º
c) 48º
d) 64º
e) 72º
Como desafio, prove que na figura acima:
AN  PQ
AN
5 1

(razão áurea)
ii.
2
MN
i.
Humanas
5