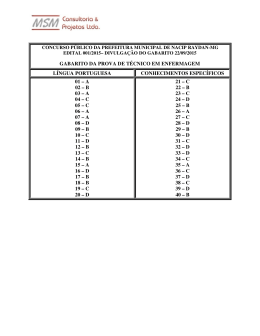
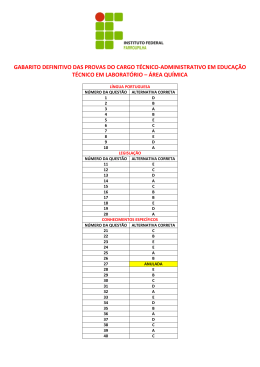
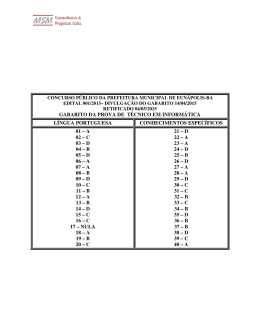
ESPECÍFICA DE MATEMÁTICA BÁSICA
Resoluções Arcos e Ângulos
Pelo “zorro” em amarelo: a = 30º. Daí, b = 50º – 30º = 20º.
EXERCÍCIOS COMPLEMENTARES
Pelo “zorro” em vermelho: c = b ⇒ c = 20º.
5.
Gabarito: a) 1,5 radianos
b) 9 cm
Resolução:
Como e + 110º = 180º ⇒ e = 70º. E pelo “zorro” em
verde: d = e ⇒ d = 70º.
Logo, x = c + d ⇒ x = 20º + 70º = 90º.
A medida de um ângulo em radianos é dada por:
comprimento do arco
. Portanto:
d=
raio

ˆ = AC= 3= 1,5 radianos .
a) AOC
OA 2


 = 9 cm.
ˆ = BD ⇒ 1,5 = BD ⇒ BD
b) DOB
OB
6
10.
Gabarito: Letra B
Resolução:
6. (UFES)
Gabarito: 45º
Resolução:
Considerando que a medida do ângulo é x, então
3(90º – x) = 180º – x ⇒ 270º – 3x = 180º – x ⇒
2x = 90º ⇒ x = 45º.
Pelo “zorro” em verde: α = a. E como “a” e “b” são
ângulos opostos pelo vértice, então a = b = α .
7.
Gabarito: Letra B
Resolução:
Pelo “zorro” em amarelo: b + 2 α = c ⇒ c = 3 α . E como “c”
e “d” são ângulos opostos pelo vértice, então c = d = 3 α
360º – x = 3(180º – (90º – x)) ⇒
360º – x = 3(180º – 90º + x) ⇒ 360º – x = 3(90º + x) ⇒
360º – x = 270º + 3x ⇒ 4x = 90º ⇒ x = 22,5º.
Pelo “zorro” em azul: d + 3 α = 60º ⇒ 6 α = 60º ⇒
α = 10º.
8. (Cesgranrio)
Gabarito: Letra E
Resolução:
11.
Gabarito: a) 120º
b) 40º
Resolução:
a)
Do triângulo pintado, tem-se que:
72º + 90º + β = 180º ⇒ β = 18º.
Como r e r’ são paralelas, então pelo “zorro” em negrito:
α = β ⇒ α = 18º .
9.
Gabarito: 90º
Resolução:
A circunferência do relógio é dividida em 12 partes
iguais, então de um número ao próximo tem-se
360º
= 30º.
12
Assim, x = 4 ⋅ 30º = 120º.
Professor Luiz Fernando
1
www.especificadematematica.com.br
Aula 13: Arcos e Ângulos
b)
Assim, o ângulo x formado pelas bissetrizes será
α β
α+β
90º
x=
+ ⇒x=
⇒x=
⇒ x = 45º .
2 2
2
2
Façamos uma regra de três para o ponteiro das horas:
ângulo
minutos
30 ⋅ 20
30º 0 60 min =
⇒α
= 10º
60
α
0 20 min
15.
Gabarito: 25º
Resolução:
Da figura tem-se que=
x 30º +α ⇒=
x 30º +10º
= 40º .
12. (Fuvest)
Gabarito: Letra C
Resolução:
Como ângulo central e arco corresponde possuem
mesma medida, então a = 20º e b = 30º.
O ângulo excêntrico interior x é a media aritmética dos
20º +30º
arcos que ele enxerga, =
então x = 25º .
2
Dividindo, entre 2 e 3, em 5 partes iguais, tem-se que
30º
cada parte mede
= 6º . O arco que está em negrito
5
tem medida de 30º + 2 ⋅ 6º = 42º.
16. (U.C.Salvador)
Gabarito: 20º
Resolução:
Façamos uma regra de três para o ponteiro das horas:
ângulo
minutos
30 ⋅ 12
30º 0 60 min =
⇒α
= 6º
60
α
0 12 min
Então, x + α = 42º ⇒ x + 6º = 42º ⇒ x = 36º.
13.
Gabarito: 118º, 120º e 122º
Resolução:
Podemos representar 3 números pares consecutivos
como sendo x – 2, x, x + 2. Logo,
O ângulo central de 80º, que está em amarelo, enxerga
o arco “a”, portanto a = 80º.
x – 2 + x + x + 2 = 360º ⇒ 3x = 360º ⇒ x = 120º.
O ângulo inscrito “b”, que está em azul, enxerga o arco
80º
de “a” de 80º, portanto b =
= 40º.
2
Logo, os ângulo são 118º, 120º e 122º.
O ângulo central b = 40º, que está em verde, enxerga o
arco “c”, portanto c = 40º.
14.
Gabarito: 45º
Resolução:
O ângulo inscrito “x” enxerga o arco de c = 40º, portanto
40º
x=
= 20º.
2
Se α e β são ângulos complementares, então
α. β = 90º. Representado α e β tem-se:
www.especificadematematica.com.br
2
Professor Luiz Fernando
Aula 13: Arcos e Ângulos
17.
Gabarito: Letra D
Resolução:
19. (U.C. Salvador)
Gabarito: Letra D
Resolução:
Como AB é lado de um pentágono, polígono de 5 lados,
 , que está em amarelo, mede
então o arco AB
360º
 = 72º .
=
AB
5
Os ângulos inscritos de 35º e “a” enxergam o mesmo
 . Assim, CD
=
arco CD
2 ⋅ 35º =
70º e a = 35º.
Como BD é bissetriz, então b = a = 35º. E o triângulo
ABC é isósceles de base BC, então c = a + b = 70º.
Como CD é lado de um hexadecágono, polígono de 16
 , que está em amarelo, mede
lados, então o arco CD
 360º
=
CD
= 22,5º .
16
Daí, do triângulo ABC,
θ+a+b=
+ c 180º ⇒ θ + 70º +70º
= 180º ⇒
=
θ 40º .
Como α é um ângulo excêntrico interior, então
72º +22,5º
=
α
= 47,25º
= 47º15 ' .
2
20. (Vunesp)
Gabarito: Letra B
Resolução:
Como β é um ângulo excêntrico exterior, então
72º − 22,5º
=
β
= 24,75º
= 24º 45 ' .
2
18. (ITA)
Gabarito: 110º
Resolução:
 . Assim,
O ângulo inscrito de 120º enxerga o arco BCF
=
BCF
2 ⋅ 120º =
240º .
.
Já o ângulo inscrito de 110º enxerga o arco CFD
=
Assim, CFD
2 ⋅ 110º =
220º .
 + CFD
 = 240º + 220º = 460º , então a parte
Como BCF
em
comum,
que
está
em
negrito,
mede


BC + EF = 360º 0 460º= 100º .

Como o ângulo B̂ de 70º é inscrito, então o arco AC

em negrito mede AC =
2 ⋅ 70º =
140º . Daí, os arcos que


estão coloridos medem AB + BC = 360º 0140º = 220º .
Logo, α que é um ângulo excêntrico interior mede
 + EF
 100º
BC
=
α
= = 50º .
2
2
Por outro lado, o ângulo inscrito que está em amarelo
 = 2α . E o ângulo inscrito que está
enxerga o arco AB
 = 2β .
em azul enxerga o arco BC
Logo, 2α +=
2β 220º ⇒ α =
+β
Professor Luiz Fernando
220º
⇒ α=
+ β 110º .
2
3
www.especificadematematica.com.br
Aula 13: Arcos e Ângulos
21.
Gabarito: 65º
Resolução:
24. (Unicamp)
Gabarito: 40.000 km
Resolução:
Como os ângulos “a” e 7,2º são opostos pelo vértice,
então a = 7,2º.
Do “zorro” em amarelo, b = a = 7,2º.
ˆ
ˆ
e EDB
tangenciam
Como os ângulos ACE
circunferência, então CO e DO são bissetrizes.
Fazendo uma regra de três:
ângulo comprimento
a
7,2º
360º
Sabe-se que raio com qualquer reta tangente forma um
ângulo de 90º, então do quadrilátero em negrito, tem-se:
50º + 90º + 2a + 2b + 90º = 360º ⇒ a + b = 65º.
0
0
800 km
x km
=
⇒x
800 ⋅ 360
= 40.000 km
7,2
25. (UnB)
Gabarito: 95
Resolução:
Daí, CÔD = a + b = 65º.
22.
Gabarito: 150º
Resolução:
Considerando um ângulo de medida x, tem-se:
x
1 
3x 
x 00 ⋅  180 0
90º
=
4
3
4 




resta
3x
4
3x
x
90º
0 60º + =
4
4
=
x 90º +60º
x = 150º
Façamos uma regra de três para a Terra:
ângulo
dias
360º 0 360 dias ⇒=
d 780º
= 2 voltas + 60º.
d
0 780 dias
23. (UFRGS)
Gabarito: Letra B
Resolução:
Como o período de translação de Marte é maior, então
ele é mais “lento” que a Terra. Deste modo, de um
alinhamento ao próximo, enquanto a Terra faz 2 voltas +
60º, Marte faz 1 volta + 60º = 420º. Assim, façamos uma
regra para Marte:
ângulo
dias
360 ⋅ 780
420º 0 780 dias=
⇒x
= 668
420
360º 0
x dias
Em semanas :
668
= 95
7
Pelo fato do espelho ser plano, a = 45º.
Do “zorro” em amarelo, b = a = 45º.
Do fato do espelho ser plano, c = b = 45º.
Do triângulo: c + d + 110º = 180º ⇒ 45º + d + 110º = 180º
⇒ d = 25º.
Do fato do espelho ser plano, e = d = 25º.
Tem-se que f + 110º = 180º ⇒ f = 70º. E do “zorro” em
azul, g = f = 70º.
Logo, α + e + g = 180º ⇒ α + 25º + 70º = 180º ⇒ α = 85º.
www.especificadematematica.com.br
4
Professor Luiz Fernando
Aula 13: Arcos e Ângulos
27. (POLI)
Gabarito: 6 horas
Resolução:
26. (UnB)
Gabarito: 1. 513
2. 108
3. 700
4. 668
Resolução:
1
Suponha que ele inicie a viagem as 8 h e x min.
Façamos uma regra de três para o ponteiro das horas:
ângulo
minutos
x
30º 0 60 min ⇒ α =
2
α
0 x min
E agora façamos uma regra de três para o ponteiro dos
minutos:
ângulo
minutos
30º 0
β 0
2
5 min
x min
⇒ β = 6x
Como de uma hora exata para a próxima tem-se 30º,
então:
x
480
β 0α = 8 ⋅ 30º ⇒ 6x 0 = 240º ⇒ x =
min
2
11
Agora, suponha que ele finalize a viagem as 14 h e y min.
Façamos uma regra de três para o ponteiro das horas:
ângulo
minutos
y
30º 0 60 min ⇒ α =
2
α
0 y min
Prolongando os raios solares e sabendo que eles são
paralelos, façamos o “Zorro”, temos que α = θ .
Logo, 12 . 9 = 108.
3
Façamos uma regra de três entre ângulo e comprimento:
ângulo comprimento
360 ⋅ 1050
9º
0 1050 km =
⇒x
= 42.000 km
9
360º 0
x km
42000
Daí,
= 700
60
E agora façamos uma regra de três para o ponteiro dos
minutos:
ângulo
minutos
30º 0
β 0
⇒ β = 6y
Como de uma hora exata para a próxima tem-se 30º,
então:
y
480
β= 2 ⋅ 30º +α + 180º ⇒ 6y=
+ 240º ⇒ y=
min .
2
11
480
Como a viagem iniciou às 8 h
min e finalizou às
11
480
14 h
min , então ela durou:
11
480
480
14 h
min – 8 h
min = 6 horas exatas.
11
11
4 Tomando 3,14 como o valor para , tem-se:
C = 2πr ⇒ 42000 = 2 ⋅ 3,14 ⋅ r ⇒ r = 6687
r
Daí,
= 668
10
Professor Luiz Fernando
5 min
y min
5
www.especificadematematica.com.br