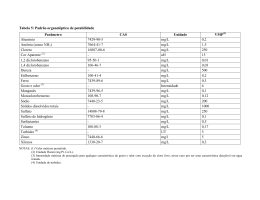
III Simpósio Brasileiro de Ciências Geodésicas e Tecnologias da Geoinformação
Recife - PE, 27-30 de Julho de 2010
p. 001 - 008
AVALIAÇÃO DO COMPORTAMENTO ESPECTRAL DA ÁGUA:
ESTUDO DE CASO DO ALTO CURSO DO RIO PARANÁ
(PRESIDENTE EPITÁCIO – SP)
FERNANDA SAYURI YOSHINO WATANABE1
NILTON NOBUHIRO IMAI1
CLÁUDIO CLEMENTE FARIA BARBOSA2
ALEX PAULO DE ARAUJO3
Universidade Estadual Paulista - UNESP
Programa de Pós-Graduação em Ciências Cartográficas, Presidente Prudente, SP1
Programa de Pós-Graduação em Geografia, Presidente Prudente2
Instituto Nacional de Pesquisas Espaciais – INPE
Departamento de Processamento de Imagens, São José dos Campos, SP3
[email protected], [email protected], [email protected], [email protected]
RESUMO – A água é um recurso natural essencial a manutenção da vida na Terra e é utilizada em
diversas atividades antrópicas, podendo-se destacar as hidrelétricas, que em muitos casos necessitam da
implantação de grandes reservatórios. Essa atividade modifica um ambiente lótico para um ambiente
lêntico ou semi-lêntico, acarretando diversos impactos sobre o ambiente aquático, no entanto, a
intensidade, bem como os processos de degradação ainda não são bem compreendidos. Nesse sentido, o
uso do sensoriamento remoto tem contribuído nos estudos desses ambientes, auxiliando a compreender
melhor a complexidade das interações que nela ocorrem. Neste estudo, realizado na represa de Porto
Primavera, município de Presidente Epitácio, foram utilizados dados hiperespectrais da água, adquiridos
com um espectrorradiômetro de campo. Os dados espectrais foram correlacionados com parâmetros de
qualidade da água, opticamente ativas, coletadas juntamente com os dados de reflectância, cujos
resultados são apresentados nesse artigo.
ABSTRACT - Water is a natural resource essential to sustain life on Earth. Many human activities
depend on this natural resource, among those the hydroelectric plants are outstanding. These hydroelectric
plants often require the deployment of large reservoirs. This activity modifies a lotic environment to a
lentic or semi-lentic, so that several impacts on the aquatic environment can happen. However, the
degradation processes and their intensities are not well known. In this sense, remote sensing data can
contribute to analyze these environments and to understand the complex interactions that occur. .In this
work, conducted in Porto Primavera Plant, city of Presidente Epitácio, hyperspectral data of the samples
of water were used and have been measured by a field spectroradiometer. The spectral data were
correlated with parameters of water quality, optically active. Some of the water quality parameters were
extracted from samples that were taken simultaneously to spectral and some limnological measuring
variables.
1 INTRODUÇÃO
A água constitui em recurso natural imprescindível
para a vida, no entanto, diversas atividades antrópicas
vêm alterando sua qualidade.
Dentre as formas de destinação desse recurso, sua
aplicação para geração de energia elétrica, obtida do
represamento de água em grandes lagos artificiais,
destaca-se pela sua importância no setor energético.
Entretanto, esses lagos artificiais provocam
grandes alterações no ambiente fluvial, cujos impactos
ainda não são bem conhecidos.
F. S. Y. Watanabe; n. N. Imai; c. C. F. Barbosa; a. P. de Araujo
Por exemplo, a alteração do nível de base tem
conseqüência na ação erosiva dos canais que sofrem essa
alteração. A ocupação de solos que antes da formação do
lago oferecia suporte ao desenvolvimento de vegetação
terrestre também pode levar ao desenvolvimento
acelerado de plantas aquáticas, graças à disponibilidade
de luz, nutrientes, entre outros fatores que contribuem
para que o ambiente se torne propício para o crescimento
dessas plantas. Além de outras conseqüências que ainda
não são tão evidentes.
Portanto, o monitoramento desses ambientes
aquáticos é fundamental para a garantia do uso
sustentável desse recurso natural. Entretanto, os
III Simpósio Brasileiro de Ciências Geodésicas e Tecnologias da Geoinformação
levantamentos de campo não permitem obter informações
adequadas sobre a distribuição espacial e temporal das
grandes massas de água formadas nos grandes
reservatórios de usinas hidrelétricas. Nesse sentido, a
combinação de dados levantados no corpo d’água com
imagens de sensoriamento remoto constituem uma das
alternativas que vem sendo adotadas para obter
informações sobre a distribuição espacial da qualidade da
água nesses reservatórios.
A fim de extrair informações de imagens de
sensoriamento remoto é necessário que se conheça melhor
o comportamento espectral da água do reservatório de
interesse. Dentro disso, o presente trabalho tem como
objetivo mostrar os resultados de uma análise da resposta
espectral de uma amostragem realizada no campo, em
condições de disponibilidade radiação eletromagnética
similares da aquisição de imagens orbitais. Essa análise
foi conduzida no sentido de avaliar duas variáveis
importantes de qualidade da água: turbidez e TSS (total
de sólidos suspensos).
2 ÁREA DE ESTUDO
A área de estudo localiza-se no alto curso do Rio
Paraná, no lado paulista, especificamente no município de
Presidente Epitácio – SP. A Figura 1 mostra a área onde
foram escolhidos os pontos de coleta das amostras.
Figura 1- Área de estudo.
Este reservatório possui uma extensa área
inundada, constituído de diferentes ambientes. A calha
principal do rio Paraná está posicionada próxima à
margem paulista. Na margem sul-mato-grossense,
identifica-se uma extensa área inundada pelo reservatório,
que incluiu áreas da antiga planície de inundação do rio
Paraná, alterando o nível de base da foz dos rios que
desaguavam nesta planície. Observou-se durante a
amostragem dos dados de campo a presença de vegetação
F. S. Y. Watanabe; n. N. Imai; c. C. F. Barbosa; a. P. de Araujo
Recife - PE, 27-30 de Julho de 2010
p. 002 - 008
imersa em pontos da planície inundada, chamadas de
“paliteiros”. Essas condições ambientais possibilitaram o
desenvolvimento de fitoplâctons e macrófitas.
3 SENSORIAMENTO REMOTO E QUALIDADE
DA ÁGUA
Cerca de 74% da superfície da Terra é coberta por
água. De toda a água encontrada no planeta, 97% de seu
volume se encontra nos grandes oceanos e apenas 0,02%
da água da Terra está presente na forma doce em
córregos, rios, lagos e reservatórios. O restante da água
encontra-se em aqüíferos (0,6%), na atmosfera terrestre
na forma de vapor d'água (0,001%) e nas coberturas de
gelo (2,2%). A água, apesar de sua abundância, apresenta
uma parcela de doce mínima, estando a maior parte na
forma salgada, bem como nas formas de neve, gelo, chuva
ou vapor d'água (Jensen, 2009).
De forma a auxiliar estudos sobre a água, várias
pesquisas e métodos de sensoriamento remoto vêm sendo
desenvolvidas, visando à obtenção de medidas espaciais
quantitativas de importantes variáveis hidrológicas
(Jensen, 2009).
Ao penetrar na coluna d’água, a radiação é
submetida a profundas alterações, tanto na sua intensidade
quanto na sua composição espectral. Segundo Jensen
(2009), a água pura não contém matéria orgânica ou
inorgânica, já os corpos d'água naturais apresentam uma
variedade desses constituintes.
A resposta espectral das águas interiores está
relacionada às substâncias presentes na coluna destes
corpos d’água, possibilitando a extração de informações
sobre as águas a partir desses dados espectrais. Estes
elementos chamados de componentes opticamente ativos
são os responsáveis pelas diferentes respostas espectrais
da água captada pelos sensores.
As águas interiores têm suas características
espectrais resultante da combinação do comportamento
espectral da água pura em conjunto com as características
de outros componentes opticamente ativos. Estes
constituintes podem ser: matéria-orgânica dissolvida,
material em suspensão, pigmentos, entre outros.
A carga de material dissolvido é constituída por
substâncias húmicas, responsável pela coloração amarela
atribuída à água. Para Rudorff (2006), a presença de
substâncias húmicas provoca uma absorção seletiva da
radiação no comprimento de ondas curtas. Já o material
em suspensão, que se constituem por minerais, partículas
finas ou grânulos em saltação, provocam um efeito de
espalhamento na coluna d’água.
Assim, mudanças nas propriedades físicas,
químicas e biológicas dos corpos de água, provocam
mudanças na interação da radiação eletromagnética com a
água e, por conseqüência, na sua cor. E neste sentido,
esses componentes opticamente tornam-se indicadores de
qualidade das águas.
4 PROCEDIMENTOS METODOLÓGICOS
Recife - PE, 27-30 de Julho de 2010
p. 003 - 008
III Simpósio Brasileiro de Ciências Geodésicas e Tecnologias da Geoinformação
As coletas de dados de campo foram realizadas no
reservatório da hidroelétrica de Porto Primavera, no
trecho próximo à cidade de Presidente Epitácio, no dia 17
de julho de 2009. A partir de um delineamento de 9
pontos, representando diferentes ambientes do
reservatório, foram realizadas a coleta de dados
limnológicos e espectrais.
Em cada ponto foram tomadas 10 medidas de
reflectância, utilizando o espectroradiômetro FieldSpec©
HandHeld com resolução espectral de 3nm e faixa
espectral de 350 a 1050 nm. Paralelamente, foram
observadas as condições ambientais de cada ponto
(iluminação, influência de ondas, ventos e informações da
coluna d’água), além da realização de amostragem direta
sobre a superfície, dos seguintes parâmetros limnlógicos:
pH, temperatura da água, oxigênio dissolvido,
condutividade e turbidez. Em 5 pontos de amostragem
estratégicos (calha do rio, confluência entre afluentes)
foram coletados 5 litros de água para posterior análise
laboratorial de sólidos em suspensão (APHA, 1998).
4.2 Processamento de dados
Os procedimentos de laboratório consistiram no
tratamento dos dados obtidos pelo espectroradiômetro,
sendo utilizadas técnicas de remoção de ruídos
(suavização das curvas espectrais) e análise derivativa.
Primeiramente, os dados foram organizados em
uma planilha de acordo com pontos amostrados.
Realizou-se uma média das 10 medidas coletadas em cada
ponto de amostragem e, em seguida, foi aplicada uma
técnica de suavização com o filtro média. Essa filtragem é
obtida do cálculo da média entre um conjunto de dados
vizinhos dos comprimentos de onda (Equação 1). Foram
aplicados os filtros de 3, 7 e 21.
S (λj) = [ Σ S (λj) ] / n
(1)
O resultado esperado da suavização por filtragem é
uma remoção do ruído, sem alteração dos detalhes
espectrais medidos. Assim, seleciona-se a dimensão da
vizinhança com base nesse critério.
Para a análise derivativa, aplicou-se uma operação
matemática de derivação dos dados (equação 2), obtendose, a partir da aplicação dessa expressão, a primeira
derivada. A segunda derivada pode ser obtida através da
derivação da primeira derivada.
dS / dλi = S (λi – S (λj)) / ∆λ
(2)
Em que ∆λ é a separação entre bandas adjacentes,
∆λ = λj - λi tal que λj > λi.
Concluído as operações de tratamento dos dados,
os resultados obtidos foram apresentados em gráficos, de
modo a facilitar a análise das curvas/feições espectrais.
4.3 Análise estatística
F. S. Y. Watanabe; n. N. Imai; c. C. F. Barbosa; a. P. de Araujo
A partir dos dados limnológicos coletados em
campo foram realizadas análises de regressão, de modo a
determinar a existência de correlação entre esses dados e
a reflectância. A análise de regressão é uma das técnicas
estatísticas mais vistas na literatura para processamento
de dados de sensoriamento remoto (RUNDQUIST et al.,
1996; ARRAUT et al., 2005).
Foi realizada análise de regressão para parâmetros
de turbidez e sólidos totais. Os cálculos de correlação e a
geração de correlogramas e de modelos de ajuste da reta
de regressão foram gerados no software Excel (Microsoft
Office).
Já os testes, de normalidade, análise de variância
(ANOVA) e análise de resíduos, foram realizados por
meio do aplicativo Minitab.
5 RESULTADOS E DISCUSSÃO
5.1 Remoção de ruído
A figura 2 mostra as curvas espectrais geradas a
partir dos dados brutos coletados em campo. Devido às
interferências
no
sinal
detectado
pelo
espectrorradiômetro, provocadas pela atmosfera e pela
reflectância especular da água, verifica-se ruídos nas
curvas espectrais.
0.08
p1
p2
0.06
Reflectância
4.1 Coletas de dados em campo
p3
p4
0.04
p5
p6
p7
0.02
p8
pmac
0
400
450
500
550
600
650
700
750
800
850
Comprimento de onda (nm)
Figura 2 – Curvas de reflectância (dados brutos)
O comportamento espectral das curvas geradas,
com exceção do ponto pmac, é semelhante, apresentando
absorção na região da luz azul, maior reflectância no
vermelho, voltando a apresentar uma alta absorção no
infravermelho. Apenas o ponto pmac apresenta um
comportamento espectral bem homogêneo por quase todo
o espectro visível, com uma reflectância um pouco maior
no comprimento da luz verde. Essa mesma curva
apresenta uma reflectância maior próximo ao
comprimento de 700 nm. Esse comportamento pode ser
uma resposta devido à presença de macrófitas submersas
nessa região (figura 3).
Recife - PE, 27-30 de Julho de 2010
p. 004 - 008
III Simpósio Brasileiro de Ciências Geodésicas e Tecnologias da Geoinformação
0.08
p1
p2
Reflectância
0.06
p3
p4
p5
0.04
p6
p7
0.02
p8
pmac
0
400
450
500
550
600
650
700
750
800
850
Comprimento de onda (nm)
Figura 5 – Filtro média com 7 pontos
O filtro de 21 pontos, no entanto, provoca uma
suavização acentuada dos dados, acarretando em perda de
parte da informação contida nas curvas (figura 6).
A curva que representa a reflectância do ponto p6
apresenta um comportamento semelhante ao do ponto p2,
porém com intensidade menor. No entanto, no
infravermelho próximo essa diferença de intensidade
entre as curvas espectrais começa a diminuir.
Os pontos p7 e p8 apresentam comportamento
espectral muito semelhante. Ambos os pontos se
encontram no canal principal do rio Paraná, onde as águas
são mais claras e visualmente apresentam coloração azul.
De modo, a facilitar a análise dos dados espectrais,
foi aplicada uma suavização desses dados, adotando
filtros média, utilizando 3 conjuntos de vizinhança
diferentes.
O filtro média de 3 pontos (figura 4) mostrou uma
baixa suavização dos dados.
0.08
p1
p2
Reflectância
0.06
p3
p4
p5
0.04
p6
p7
0.02
p8
pmac
0
400
450
500
550
600
650
700
750
800
850
Comprimento de onda (nm)
Figura 4 – Filtro média com 3 pontos
O filtro média de 7 pontos (figura 5) apresentou o
melhor resultando dentre todos os filtros aplicados,
reduzindo de forma satisfatória a influência do ruído das
curvas espectrais, mantendo o nível de informação dos
dados.
F. S. Y. Watanabe; n. N. Imai; c. C. F. Barbosa; a. P. de Araujo
0.08
p1
p2
0.06
p3
Reflectância
Figura 3 – Macrófitas submersas no ponto pmac
p4
p5
0.04
p6
p7
p8
0.02
pmac
0
400
450
500
550
600
650
700
750
800
850
Comprimento de onda (nm)
Figura 6 – Filtro média com 21 pontos
5.2 Análise derivativa
A partir do resultado do filtro média de 7 pontos,
que apresentou o melhor desempenho, sem grandes
perdas de informação espectral, foram aplicadas outras
técnicas de processamento de dados.
A figura 7 mostra o resultado da aplicação da
derivada de primeira ordem sobre os dados de
reflectância.
A primeira derivada elimina o sinal de fundo,
remove a sobreposição de feições espectrais e realça os
componentes de menor intensidade que compõem o
espectro (BARBOSA et al., 2005), sendo adequada a sua
aplicação em estudos de sólidos suspensos, bem como de
pigmentos fotossintetizantes.
Todos os pontos apresentam um pico negativo
próximo ao comprimento de onda de 600 nm a 650 nm. O
ponto pmac apresenta o comportamento mais diferente
em relação aos demais pontos amostrados, com um pico
positivo próximo a 700 n, enquanto os outros pontos
apresentam valores negativos nesse comprimento. Esta
característica está associada a influência de macrófitas
sobre a resposta da reflectância no ambiente aquático.
Recife - PE, 27-30 de Julho de 2010
p. 005 - 008
III Simpósio Brasileiro de Ciências Geodésicas e Tecnologias da Geoinformação
0.0004
p1
1ª derivada
p2
0
p3
400
450
500
550
600
650
700
750
800
850
p4
p5
-0.0004
Nesse sentido, foi feita e analisada a correlação
dessa variável com sua respectiva resposta espectral em
cada ponto amostrado. A Figura 9 mostra o correlograma
para esta variável em relação aos valores obtidos com a
derivada de primeira ordem.
p6
p7
p8
-0.0008
1
pmac
Comprimento de onda (nm)
Figura 7 – Primeira derivada das curvas espectrais
De modo a remover a influência dos sedimentos da
curva (RUNDQUIST et al., 1996), foi aplicada a derivada
de segunda ordem sobre os dados de reflectância
suavizados (figura 8).
Coeficiente de correlação
-0.0012
0.8
0.6
0.4
0.2
0
-0.2400
450
500
550
600
650
700
750
800
850
-0.4
-0.6
-0.8
-1
Comprimento de onda (nm)
Figura 9 – Correlação entre reflectância e turbidez
0.00015
p1
0.0001
p3
0.00005
p4
p5
0
837
814
791
768
745
722
699
676
653
630
607
584
561
538
515
492
469
446
423
p6
400
2ª derivada
p2
p7
p8
-0.00005
pmac
-0.0001
Comprimento de onda (nm)
Figura 8 – Segunda derivada das curvas espectrais
Nota-se um pico positivo próximo a 600 nm
(vermelho), correspondente a uma pequena absorção
nessa região que pode ser observada nas curvas da figura
5 e a um pequeno pico na primeira derivada (figura 7).
Absorções nessa região espectral, geralmente, estão
relacionadas
com
a
presença
de
pigmentos
fotossintetizantes.
De maneira geral, o resultado alcançado com a
segunda derivada possibilitou o realce de outras
informações dos dados amostrados, já que a baixa taxa de
variação existente na primeira derivada confere-lhe esta
característica.
4.3 Análise de correlação
Os dados limnológicos coletados em campo
podem ser observados na Tabela 1. Dentre os parâmetros
de qualidade de água adquiridos in situ, somente a
turbidez é opticamente ativa.
Tabela 1 – Dados limnológicos
F. S. Y. Watanabe; n. N. Imai; c. C. F. Barbosa; a. P. de Araujo
A correlação da turbidez em relação à refletância
foi analisada no intervalo de 400 nm a 850 nm. Verificase que a correlação é positiva entre cerca de 400 a 580 e
negativa de 581 a 740 nm, havendo uma oscilação entre
os sinais do restante do espectro analisado.
Os maiores coeficientes de correlação da turbidez
se encontram nos comprimentos de 537 nm (R = 0,9567)
e 707 nm (R = -0,9681).
Dessa forma, ajustou-se um modelo de regressão
que relaciona os dados de turbidez em função da resposta
espectral obtida. Para sua realização, primeiramente, foi
feita uma Análise de Variância (ANOVA), de modo a
testar a normalidade dos dados. A partir do software
Minitab foram gerados a Tabela 2, permitindo-se analisar
a estatística F e o p-valor.
Tabela 2 – Análise de variância para dados de reflectância
de turbidez
Source
Regression
Residual
Error
Total
DF
1
SS
4,44255E-07
MS
4,44255E-07
7
8
2,10620E-08
4,65317E-07
3,00886E-09
F
147, 65
P
0,000
Adotando-se um α de 0,05 para o p-valor, verificase que há normalidade dos dados obtidos em campo. De
acordo com a Tabela 2, o p-valor obtido é inexpressível, o
que permite rejeitar a hipótese H0, ou seja, os coeficientes
do modelo de regressão ajustado determinam os valores
de reflectância e, portanto, o modelo se mostra adequado.
Vê-se também que a estatística F é maior do que o valor
especificado para F com uma variável e 7 graus de
liberdade (5,59), corroborando o resultado obtido com o
p-valor.
Dessa forma, foi gerada a regressão para os dados
de turbidez e refletância, sendo este último referente aos
dados da primeira derivada, como mostra a Figura 10.
Recife - PE, 27-30 de Julho de 2010
p. 006 - 008
III Simpósio Brasileiro de Ciências Geodésicas e Tecnologias da Geoinformação
0.0002
0
1ª derivada
0
3
6
9
12
15
18
-0.0002
-0.0004
-0.0006
y = -6E-05x + 0.0002
R2 = 0.9547
-0.0008
Entretanto, considerando-se que o conjunto de
dados é composto por apenas 9 observações e que os
dados apresentam uma normalidade, pode-se considerar
que o resultado obtido é muito satisfatório.
Além dos dados de turbidez, outra variável
opticamente ativa foi correlacionada à reflectância, os
TSS, obtidos em laboratório. A Tabela 3 mostra os
valores desse parâmetro para os pontos, onde foram
coletadas amostras de água para análise.
Turbidez (NTU)
Analisando a Figura 10, verifica-se um ótimo valor
para R2, de 95,5%. O desvio padrão, de 0,0000548531,
também pode ser considerado muito bom.
A primeira derivada elimina a influência da água
sobre as curvas espectrais, facilitando a análise de sólidos
(GOODIN et al., 1993; ARRAUT et al., 2005).
Nesse sentido, pode confirmar, para este caso, que
a variável independente (primeira derivada) explica de
forma satisfatória o índice de turbidez no corpo d’água.
De modo a verificar a qualidade e coerência do
modelo de regressão ajustado para os dados empregados
na análise foi feito a análise dos resíduos. A Figura 11
apresenta os resultados obtidos.
Tabela 3 – Dados de sólidos suspensos totais (TSS)
A partir dos dados de sólidos suspensos totais foi
gerado um correlograma, representado na Figura 12.
1
0,8
Coeficiente de correlação
Figura 10 – Reta de regressão ajustada para os valores de
turbidez em função da primeira derivada no comprimento
de onda 707 nm.
0,6
0,4
0,2
0
-0,2 400
450
500
550
600
650
700
750
800
850
-0,4
-0,6
-0,8
-1
Comprimento de onda (nm)
Figura 12 – Correlação entre reflectância e TSS
O comprimento de onda mais correlacionado
apresentado foi o de 811 nm com uma correlação de
0,9889. Para dos valores de reflectância obtidos nos
pontos onde foram amostrados TSS realizou-se ANOVA
(Tabela 4) e teste de normalidade dos dados.
Tabela 4 – ANOVA para reflectância e TSS
Figura 11 – Análise de resíduos para modelo de regressão
entre reflectância e turbidez
Analisando a Figura 11, observa-se no gráfico que
a probabilidade normal e de ordem apresentam resultados
muito bons. O primeiro apresenta os resíduos bem
próximos à linha de ajuste e o segundo possui uma
distribuição bem aleatória dos resíduos, como o esperado
para ambos os casos.
No entanto, em relação ao histograma e o ajuste de
resíduos, eles não apresentam resultados muito
satisfatórios. No primeiro caso, esperava-se uma
distribuição dos resíduos com características de
normalidade, o que não é observado. Quanto ao ajuste, os
resíduos que se encontram na área positiva do gráfico não
apresentam uma distribuição aleatória.
F. S. Y. Watanabe; n. N. Imai; c. C. F. Barbosa; a. P. de Araujo
Source
Regression
Residual
Error
Total
DF
1
SS
4,01250E-08
MS
4,01250E-08
3
4
8,87782E-10
4,10128E-08
2,95927E-10
F
135, 59
P
0,001
Admitindo-se um p-valor de 0,05, analisando os
dados presentes na Tabela 4, verifica-se que existe
normalidade entre os dados de reflectância. O p-valor
apresenta valor menor a 0,05 e a estatística F é maior a
10,13, podendo-se rejeitar a hipótese H0, ou seja, a
variável é significativa, logo o modelo é adequado.
Uma vez que há normalidade dos dados, foi
ajustada uma reta de regressão para os dados de
reflectância, referente à primeira derivada (ARRAUT et
al., 2005), e sólidos suspensos totais, como mostra a
Figura 13.
III Simpósio Brasileiro de Ciências Geodésicas e Tecnologias da Geoinformação
0,00015
1a derivada
0,00010
0,00005
0,00000
0,1
0,15
0,2
0,25
0,3
0,35
0,4
-0,00005
-0,00010
y = -0,0011x + 0,0003
R2 = 0,978
-0,00015
Sólidos Suspensos Totais (mg/L)
Figura 13 – Reta de regressão ajustada para TSS em
função da 1ª derivada para λ igual a 811 nm
O modelo de regressão gerado apresenta um R2 de
97,8%, considerado um ótimo valor. Para confirmação da
coerência do ajuste, os resíduos dos dados foram
analisados. Os resultados obtidos estão apresentados na
Figura 14.
Recife - PE, 27-30 de Julho de 2010
p. 007 - 008
Modelos de regressão ajustados mostram que é
possível inferir ambas variáveis limnológicas, na área de
estudo, com base nas suas respostas espectrais, sendo que
a faixa do infra-vermelho próximo mostrou-se melhor
correlacionado. As respostas espectrais medidas que
possuem maior correlação com a variável turbidez se
encontram nos comprimentos de 537 nm (R = 0,9567) e
707 nm (R = -0,9681). No caso do TSS foi no
comprimento de onda de 811 nm com uma correlação de
0,9889. Outros levantamentos e análises devem ser
realizados a fim de conhecer melhor os intervalos
espectrais que melhor se correlacionam com essas
variáveis limnológicas.
A presença de macrófitas submersas modifica
totalmente o comportamento das curvas, pois a radiação
passa a apresentar uma mistura da resposta espectral da
água e das plantas aquáticas. Esse comportamento pode
ser verificado no ponto pmac, onde as curvas espectrais se
diferenciam de todas as demais.
A primeira derivada mostrou-se uma ferramenta
importante na análise dos dados estudados, acentuando
informações vistas nas curvas espectrais. A segunda
derivada, geralmente relacionada com clorofila, apresenta
poucas informações. Isso pode indicar que possa haver
uma baixíssima concentração desses pigmentos. A alta
oscilação das curvas, também, dificulta a extração de
informações do gráfico. Para que as feições sejam
melhoradas, em trabalhos futuros, talvez seja interessante
remover ainda mais os ruídos ou aplicar outras técnicas de
pré-processamento nos dados brutos.
AGRADECIMENTOS
Figura 14 – Análise de resíduos para modelo de regressão
entre reflectância e TSS
Mesmo com um conjunto amostral com
pouquíssimas observações, verifica-se que os resíduos da
regressão entre reflectância e TSS apresentaram
resultados consistentes. As distribuições dos resíduos
apresentados no gráfico de probabilidade normal estão
próximas da linha de ajuste, mostrando que o modelo de
regressão é coerente. O histograma dos resíduos apresenta
um comportamento de distribuição normal melhor em
relação ao ajuste obtido para os dados de turbidez. Já os
gráficos de valores ajustados e ordem dos dados versus o
resíduo não apresentam uma aleatoriedade tão boa. No
entanto, considerando uma análise com poucos dados
amostrais, pode-se confirmar um ajuste eficiente.
6 CONCLUSÕES
A correlação entre os dados de turbidez e
reflectância pode ser considerada muito boa, baseada nos
parâmetros estatísticos analisados. Pode-se concluir
também que as águas do rio Paraná, no trecho estudado,
apresentam baixa turbidez, o que reflete em sua resposta
espectral.
F. S. Y. Watanabe; n. N. Imai; c. C. F. Barbosa; a. P. de Araujo
Os autores agradecem ao PROCAD pelo auxílio
financeiro na coleta dos dados em campo.
Agradece também ao Programa de Pós-Graduação
em Ciências Cartográficas, da UNESP, de Presidente
Prudente, pelo auxílio financeiro. E, finalmente, ao CNPq,
pela bolsa de mestrado.
REFERÊNCIAS
APHA. Standard Methods for the Examination of
Water and Wastewater. 20th ed. Washington: APHA,
1998.
ARRAUT, E. M.; RUDORFF, C. M.; BARBOSA, C. C.
F.; CARVALHO, J. C.; PEREIRA FILHO, W.; NOVO,
E. M. L. M. Estudo do comportamento espectral da
clorofila e dos sólidos em suspensão nas águas do Lago
Grande de Curuai (Pará), na época da seca, através de
técnicas de espectroscopia de campo. In: Anais XII
Simpósio Brasileiro de Sensoriamento Remoto.
Goiânia. São José dos Campos: INPE, 2005. p. 2447 –
2456.
BARBOSA, C. C. F. Sensoriamento remoto da dinâmica
da circulação da água no sistema planície de Curuai/Rio
Amazonas. 2005. 281f. Tese (Doutorado em
III Simpósio Brasileiro de Ciências Geodésicas e Tecnologias da Geoinformação
Sensoriamento Remoto) – Instituto Nacional de Pesquisas
Espaciais, São José dos Campos.
GOODIN, D. G.; HAN, L.; FRASER, R. N.;
RUNDQUIST, C.; STEBBINS, W. A.; SCHALLES, J. F.
Analysis of suspended solids in water using remotely
sensed
high
resolution
derivative
spectra.
Photogrammetric Engineering and Remote Sensing.
Vol. 59, n. 4, p. 505 – 510, 1993.
JENSEN, J. R. Sensoriamento remoto do ambiente:
uma perspectiva em recursos terrestres. 2a Edição. São
José dos Campos: Parênteses, 2009.
RUDORFF, C. M. Estudo da composição das águas da
planície amazônica por meio de dados de reflectância
do sensor Hyperion/EO-1 e de espectrorradiômetro de
campo visando à compreensão da variação temporal
dos seus constituintes opticamente ativos. 2006. 140p.
Dissertação (Mestrado em Sensoriamento Remoto) –
Instituto Nacional de Pesquisas Espaciais, São José dos
Campos.
RUNDQUIST, D. C.; HAN, L. H.; SCHALLES, J. F.;
PEAKE, J. S. Remote measurement of algal chlorophyll
in surface waters: the case for the first derivate of
reflectance near 690 nm. Photogrammetric Engineering
and Remote Sensing. FEB, 1996. p. 195-200.
F. S. Y. Watanabe; n. N. Imai; c. C. F. Barbosa; a. P. de Araujo
Recife - PE, 27-30 de Julho de 2010
p. 008 - 008