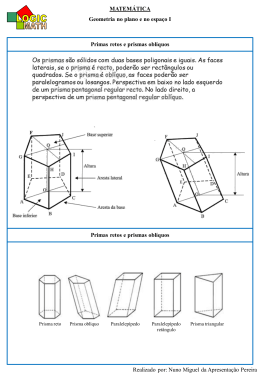
O USO DE PROGRAMAS COMPUTACIONAIS COMO RECURSO
AUXILIAR PARA O ENSINO DE GEOMETRIA ESPACIAL
Angélica Menegassi da Silveira – UNIFRA
Eleni Bisognin - UNIFRA
Resumo: O presente artigo tem como objetivo apresentar alguns resultados parciais de
uma dissertação de mestrado profissional sobre o ensino de Geometria Espacial, no Ensino
Médio, referentes às contribuições do uso de recursos computacionais como os programas
Cabri 3D e Macromedia FLASH 8 para compreensão dos conceitos e exploração das
propriedades dos sólidos geométricos. Foram selecionadas algumas atividades que foram
aplicadas em sala de aula e pode-se concluir da análise dos resultados obtidos, que o uso
destes recursos auxiliou ao aluno tornar-se mais autônomo e que estas ferramentas
auxiliaram na melhoria do ensino e da aprendizagem da Geometria.
INTRODUÇÃO
Pesquisas em Educação Matemática têm mostrado que os recursos tecnológicos vêm
proporcionando mudanças no Ensino de Matemática e, em particular, no Ensino de Geometria.
A utilização do computador e dos softwares educacionais, como recursos pedagógicos auxiliam
os professores a tornar as aulas mais atraentes e resgatando o interesse do aluno pelo estudo da
Matemática. No Ensino de Geometria o uso de softwares educacionais oferece muitas
potencialidades, pois podem criar um ambiente rico de imagens, sons e animações, fornecendo
dessa maneira, um estudo mais dinâmico e permitindo que o aluno visualize, interaja com o
computador, construa e experimente. Diante do computador os alunos procuram as soluções para os
seus problemas e dessa maneira constroem seus próprios conhecimentos.
O uso desses recursos tecnológicos vem proporcionando mudanças não só na área
educacional, no processo de ensino e aprendizagem da Matemática, mas em todos os setores da
sociedade. Quando usados adequadamente, esses recursos facilitam a construção de conhecimentos
geométricos de maneira significativa. A interface dinâmica, a interatividade que esses programas
propiciam e os recursos de manipulação e movimento das figuras geométricas que se apresentam na
tela do computador, contribuem no desenvolvimento de habilidades em perceber diferentes
representações de uma mesma figura, levando desta maneira a descoberta das propriedades das
figuras geométricas estudadas. Nos ambientes de geometria dinâmica, com a possibilidade de
movimentar e analisar o objeto estudado sob diferentes ângulos, os alunos têm a possibilidade de
explorar as propriedades do objeto levando-o a experimentar, testar hipóteses, desenvolver
estratégias, argumentar, deduzir.
De acordo com (King e Schattshneider, 1997), alguns dos principais benefícios e aplicações
de um sistema computacional de Geometria Dinâmica são:
(i) A construção, manipulação e a transformação de objetos espaciais que permitem aos
usuários explorar a geometria, de forma que novas relações e propriedades sejam descobertas.
(ii) O desenvolvimento do conhecimento do espaço: planificação de sólidos geométricos, bem
como o cálculo de áreas e volumes em espaços virtuais.
De acordo com os (PCN’s,1998), a formação do aluno deve ter como objetivo central a
aquisição dos conhecimentos básicos e o desenvolvimento de capacidades tais como: de pesquisar,
buscar informações, selecioná-las e analisá-las ; a capacidade de formular hipóteses, verificá-las e
testá-las. Neste sentido, o uso de softwares computacionais auxilia o professor de Matemática a
transformar sua aula numa aula investigativa facilitando a criação de situações–problema que
servem de motivação e de desafio aos alunos.
Neste trabalho são apresentados alguns resultados de uma experiência realizada, a partir da
aplicação de uma Seqüência de Ensino, elaborada seguindo algumas etapas da metodologia da
Engenharia Didática e utilizando-se recursos tecnológicos no ensino de Geometria Espacial, com
alunos do Ensino Médio, de uma escola pública de Santa Maria, RS. Optou-se em utilizar o
software geométrico Cabri 3D, o qual é uma ferramenta que auxilia no ensino da Geometria e é
utilizado tanto no Ensino Médio como no Ensino Superior. O Cabri 3D é um ambiente de geometria
dinâmica em três dimensões que possibilita a construção e manipulação de sólidos geométricos o
qual juntamente com o Macromedia Flash 8 auxilia na exploração dos mesmos.
A ATIVIDADE EM SALA DE AULA
As atividades descritas neste trabalho fazem parte de uma Seqüência Didática a qual foi
elaborada seguindo algumas etapas da Engenharia Didática.
Segundo (ARTIGUE, 1995), a Engenharia Didática se caracteriza por ser: “como um esquema
experimental baseado em "realizações didáticas" em sala de aula, isto é, sobre a concepção, a
realização, a observação e a análise de Seqüências de Ensino”.
Neste artigo são apresentadas duas atividades que foram desenvolvidas em sala de aula, com
alunos do Ensino Médio, sobre o cálculo do volume do prisma e da pirâmide utilizando o Princípio
2
3
de Cavalieri e com o auxílio do programa Cabri 3D e Macromedia Flash 8, as quais são um recorte
da Seqüência Didática que fazem parte da Dissertação de Mestrado Profissionalizante em Ensino de
Matemática, da autora. Para a elaboração desta Seqüência Didática foi feito, primeiramente, um
levantamento sobre as concepções dos alunos e as dificuldades e obstáculos referentes ao processo
ensino-aprendizagem da geometria espacial. Para obtenção dessas informações foi aplicado um
teste diagnóstico composto de exercícios de Geometria Espacial com o propósito de averiguar os
conhecimentos dos alunos sobre a compreensão dos conceitos e propriedades dos sólidos
geométricos. Utilizou-se, também o modelo de Van Hiele como suporte teórico para analisar o
desenvolvimento do pensamento em Geometria (Van Hiele, 1986; Kaleff et all, 1994; Nasser,
1997).
Atividade 1- Determinação do volume de um prisma.
O propósito dessa atividade foi determinar o volume de um prisma utilizando-se o Princípio
de Cavalieri. Este princípio diz que: dois sólidos S1 e S2, de mesma altura h e com bases de áreas
iguais, contidas num mesmo plano α, têm mesmo volume se, qualquer plano α paralelo a β,
determinar nos sólidos S1 e S2, seções transversais com áreas iguais.
Utilizando-se o Princípio de Cavalieri, comparou-se o volume de um prisma triangular
com um paralelepípedo cujas bases possuem a mesma medida, conforme mostrado na Figura 1
abaixo.
β
α
Figura 1 – Comparação do volume do paralelepípedo e do prisma triangular.
Como as seções paralelas determinadas pelos planos possuem mesma área e os dois sólidos
têm a mesma altura, pelo Princípio de Cavalieri conclui-se que eles possuem o mesmo volume.
Comparações semelhantes feitas com outros prismas, cuja área da base possui a mesma medida da
área da base do paralelepípedo, pode-se concluir, neste caso, que,
Vprisma = Vparalelepípedo
Portanto, o volume do prisma é o produto da medida da área da base pela medida da altura,
isto é,
Vprisma = Abase x altura
A determinação do volume de um prisma pentagonal ou hexagonal foi feita utilizando-se o
cálculo do volume do prisma triangular. O recurso computacional utilizado como Cabri 3D
permitiu uma melhor visualização, como mostrado nas Figuras 2 e 3 abaixo, e o Flash 8 permitiu
mostrar por meio do movimento das partes a composição ou decomposição do prisma pentagonal e
do prisma hexagonal em 5 e 6 primas triangulares respectivamente.
A Figura 2 e 3 mostram a decomposição do prisma pentagonal e hexagonal em prismas
triangulares e, a partir do volume do prisma triangular, os alunos calcularam o volume do prisma
pentagonal e do prisma hexagonal.
Figura 2 – Prisma pentagonal
4
5
Figura 3 – Prisma hexagonal
Uma contribuição significativa do software Cabri 3D e do Flash 8 para apropriação dos
conceitos geométricos foi a possibilidade de movimentação das figuras, no caso os prismas de bases
formadas por diferentes formas geométricas, oportunizando seu tratamento de forma diferenciada,
favorecendo o reconhecimento das propriedades particulares do sólido. Nas atividades utilizando o
software Cabri 3D, os alunos puderam manipular as figuras e interagir com os colegas para definir e
se apropriar de conceitos e propriedades dos prismas. No início de cada atividade a professora deu
as explicações e orientações necessárias para o desenvolvimento da atividade e deixou os grupos
interagirem, intervindo somente no momento de necessidade. As observações sobre as interações e
apropriações dos conceitos foram anotadas para posterior análise. Ao final de cada atividade, foram
reunidas as construções e definições dos grupos para analisar os conceitos e as propriedades
deduzidas referentes à atividade proposta.
Atividade 2- Determinação do volume da pirâmide triangular.
O propósito desta atividade foi calcular o volume da pirâmide de base triangular a partir do
volume do prisma triangular
Considerou-se primeiramente o prisma triangular conforme a Figura 4, a seguir.
Figura 4 – Prisma triangular
A partir do prisma triangular e com auxílio de recursos do programa computacional este
prisma foi decomposto em 3 pirâmides triangulares como mostrado na Figura 5 abaixo.
Figura 5 – Decomposição do prisma em três pirâmides triangulares.
A visualização da decomposição do prisma triangular em 3 pirâmides triangulares permitiu a
concluir que, se as bases triangulares do prisma e das pirâmides possuem mesma área então,
Volume pirâmide = 1/3 Volume do prisma
Observou-se que resultados como esse relacionado à determinação do volume dos prismas e
pirâmides, cuja dedução foi facilitada pelo uso do software Cabri 3D, trouxeram contribuições
importantes quanto à construção de conceitos e verificação das propriedades, compreensão do
6
7
cálculo do volume, embora a utilização dessas ferramentas computacionais exigisse dos alunos
novas habilidades quanto ao manuseio dessas ferramentas e novas posturas diante da aprendizagem
no sentido da autonomia e independência intelectual.
CONSIDERAÇÕES FINAIS
Nosso propósito nesse trabalho foi apresentar algumas atividades de Geometria Espacial para o
Ensino Médio, destacando a importância do uso de programas computacionais como Cabri 3D e
Flash 8 como uma alternativa para ensinar e aprender o conteúdo de sólidos geométricos.
Criar diferentes estratégias de ensino com o auxílio da tecnologia, numa proposta pedagógica
que tenha como centro o aluno, foi também uma de nossas preocupações. Podemos concluir que o
uso de recursos computacionais auxiliou os alunos a serem mais autônomos, pois possibilitou
construir e visualizar os sólidos geométricos oportunizando a descoberta das propriedades e a
exploração de suas relações.
Podemos concluir, também, que as representações dinâmicas propiciadas pelos softwares Cabri
3D e Flash 8 foram importantes na construção dos conceitos e nas deduções das propriedades dos
prismas e das pirâmides bem como no cálculo do volume desses sólidos. Essas observações e
conclusões propiciaram uma reflexão sobre o uso dos softwares de geometria dinâmica em
atividades de ensino e suas potencialidades em propostas pedagógicas com esses recursos e de que
forma esses recursos tecnológicos contribuem para a apropriação do significado dos conceitos
geométricos.
Referências
Artigue, M; Douady,R; Moreno, L.(1995) Ingeniería Didáctica em Educación Matemática: un
esquema para la investigación y la innovación en la enseñanza y el aprendizaje de las
matemáticas. México: 1. ed.
BRASIL. Ministério da Educação, Secretaria de Educação Média e Tecnológica. Parâmetros
curriculares nacionais: ensino médio. Brasília. MEC. 1999; BRASIL. Ministério da Educação,
Secretaria de Educação Média e Tecnológica. PCN+- ensino médio, orientações educacionais
complementares aos parâmetros curriculares nacionais. Brasília. 2002.Disponível em:
<http://www.sbfisica.org.br/ensino/pcn.shtml>. Acesso em: 10 set. 2007.
King, J. e Shattschneider,D; (1997). Geometry Turned On - Dynamic Software in Learning,
Teaching and Research, Washington: Mathematical Association of America.
Kaleff, A.M; Henriques, A; Reid, M; Figueiredo,L.G; (1994) Desenvolvimento do pensamento
geométrico: modelo de Van Hiele. Bolema, Rio Claro, v.10, p.21-30.
Nasser,L; (1997).Geometria segundo a teoria de Van Hiele. Rio de Janeiro: Projeto Fundão.
Van Hiele, P.,(1986). Structure and Insight: a theory of mathematics education. New York:
Academics Press.
8