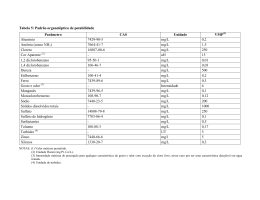
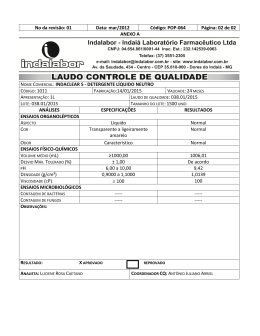
DETERMINAÇÃO DO COEFICIENTE DE VARIAÇÃO DA PERDA DE CARGA COM O TEMPO NA
FILTRAÇÃO RÁPIDA
Arantes do Nascimento Teixeira Bernardo
Departamento de Engenharia Civil, Universidade Federal de São Carlos
Rod. Washington Luis, km 235
13.565-905 - São Carlos - SP - BRASIL
Tel./Fax : 55 16 2748259
E-mail : [email protected]
RESUMO
A variação da perda de carga com o tempo nos filtros rápidos é um parâmetro importante, que depende
das características físicas do meio filtrante, da qualidade da água e da taxa de filtração. O objetivo deste
trabalho, foi o de estudar uma relação simplificada entre estes parâmetros, possibilitando a previsão da
variação da perda de carga em um determinado filtro ao longo do tempo. Foi estudado um “ coeficiente de
variação da perda de carga com o tempo” (coeficiente “ a” ), que teria um valor típico para cada meio
filtrante. A qualidade da água foi representada por sua turbidez. Para testar a relação entre os parâmetros,
foram operados filtros pilotos trabalhando com taxa constante e com taxa declinante variável, ambos com o
mesmo meio filtrante. As perdas de carga iniciais (Ho) e ao longo do tempo (H(t)), a turbidez do afluente
(Co) e do efluente (C), bem como a taxa de filtração (v), foram os parâmetros de controle. Os resultados
indicaram que a relação H(t)=Ho+(a.Co.v)t levou à obtenção de valores do coeficiente “ a” que não
diferiam significativamente entre si, quando a medição da turbidez era feita por um mesmo equipamento.
Concluiu-se que o referido coeficiente refletiu o comportamento do meio filtrante estudado, e que a relação
estabelecida entre os diversos parâmetros mostrou-se adequada. A turbidez, embora tenha a vantagem de
ser medida com facilidade, constituiu-se no parâmetro mais sujeito a incorreções, recomendando-se mais
investigações para a superação desta limitação.
Palabras clave: tratamento de água,filtração rápida, perda de carga
INTRODUÇÃO
O aumento, ao longo do tempo, da perda de carga nos meios filtrantes, como consequência da retenção de
partículas presentes na água, é um fator determinante no projeto e operação de unidades de filtração
rápida. A altura da caixa do filtro, as variações do nível d'água acima do material filtrante, a duração das
carreiras de filtração, os intervalos entre lavagens, as características do equipamento controlador de vazão,
são alguns dos parâmetros que estão diretamente relacionados com aquele fenômeno, que ocorre para
qualquer tipo de operação do filtro (taxa constante ou declinante, nível constante ou variável).
Na filtração com ação de profundidade, a variação da perda de carga é decorrente da diminuição da
porosidade do meio filtrantre, que tem os seus vazios ocupados pelas partículas retidas. A maneira como
isto ocorre é função das características do material filtrante (tamanho, forma e grau de uniformidade dos
grãos, porosidade inicial) e da suspensão sendo filtrada (quantidade e tipos de partículas retidas). É
importante observar que a taxa de filtração influi na variação da perda de carga por determinar a
quantidade de partículas que atingem o filtro por unidade de tempo. De modo geral, pode-se considerar que
as características relacionadas com os materiais filtrantes permanecem inalteradas ao longo da sequência
de operações dos filtros (a menos que ocorram desgaste, quebra ou perda de grãos). As características da
suspensão, por sua vez, podem variar continuamente, à medida em que se alteram a quantidade ou o tipo
de partículas presentes na água a ser filtrada. Estas alterações podem se dar na própria água bruta ou nas
dosagens de produtos químicos, especialmente os coagulantes e auxiliares.
Pode-se considerar, portanto, que, definidas as características físicas de um filtro e mantendo-se a taxa de
filtração constante, a variação da perda de carga seja função apenas da quantidade de partículas retidas.
Conhecendo-se este parâmetro, pode-se prever o crescimento da perda de carga com o tempo. A principal
dificuldade reside na escolha de um parâmetro que seja representativo e de fácil obtenção.
Teoricamente, o depósito específico (σ = volume de partículas retidas/volume de meio filtrante) é o mais
indicado, sendo muito empregado em diversos modelos de filtração. Sua determinação, porém, é bastante
complexa. Seria interessante a utilização de um parâmetro que pudesse ser obtido diretamente de
amostras de água, e neste sentido a turbidez apresenta-se, em função da sua facilidade de medição e de
seu largo emprego, como uma das alternativas mais favoráveis.
OBJETIVO
O presente trabalho teve por objetivo determinar uma relação que represente, na filtração rápida, a
variação da perda de carga com o tempo, incluindo um coeficiente que seria característico para cada meio
filtrante e empregando a turbidez para quantificar as partículas presentes na água a ser filtrada.
METODOLOGIA
A determinação do coeficiente de variação da perda de carga foi realizada a partir de ensaios em
instalações experimentais, cujos principais componentes eram colunas de filtração em acrílico
transparente, com 91 mm de diâmetro interno e 3,6 m de altura, As instalações completas são descritas
em maiores detalhes em TEIXEIRA (1991). As linhas de alimentação e de saída dos filtros pilotos eram
modificadas de modo a permitir a realização de ensaios sob duas condições de operação:
a) filtros com taxa constante e nível variável (TC), operando com 4 unidades independentes;
b) sistema de filtração com taxa declinante (SFTD), com 4 unidades interligadas.
Ambos utilizaram o mesmo meio filtrante, constituido unicamente por areia (menor grão = 0,7 mm; maior
grão = 2,0 mm; tamanho efetivo = 0,9 mm; coeficiente de desuniformidade = 1,33; altura da camada = 1,25
m). Os filtros com taxa constante foram operados com 200, 250, 300, 350, 400, 450, 500, 550 e 600 m/d,
enquanto o SFTD trabalhou com taxas médias de 250, 300 e 350 m/d. O afluente era água decantada de
uma estação de tratamento completo. Foram medidas a turbidez do afluente e efluentes, em alguns
ensaios com turbidímetro de bancada, em outros com turbidímetro de escoamento contínuo. As perdas de
carga totais e ao longo do meio filtrante foram medidas através de tubos piezométricos. As vazões foram
monitoradas e ajustadas através de medições volumétricas, com o auxílio de rotâmetros.
A metodologia para a determinação do coeficiente de variação da perda de carga baseou-se no método de
análise racional simplificada proposto por IVES (1963). Basicamente, este consiste em se associar o
aumento linear das perdas de carga totais a uma reta com equação do tipo:
H ( t ) = Ho + ( a .Co .v ) t
onde:
H(t)
Ho
a
Co
v
(1)
: perda de carga total no tempo t (expressa como altura de líquido, L);
: perda de carga total inicial (L);
: coeficiente de variação da perda de carga total (dimensão inversa a Co);
: concentração de partículas afluentes ao filtro (neste caso, turbidez) (UT);
: taxa de filtração (L/T).
A hipótese assumida foi a de que o valor do coeficiente a deveria permanecer constante para um
determinado meio filtrante. Desta maneira, obtendo-se o valor deste parâmetro, pode-se prever o
comportamento da perda de carga no filtro em questão para diferentes valores das outras variáveis.
Para cada um dos ensaios realizados, o valor de v era fixado e, mesmo no caso do SFTD, mantinha-se
constante no intervalo entre lavagens; o valor de Ho era medido diretamente, no início da operação; o valor
de Co era calculado a partir da média aritmética dos diferentes valores ao longo do tempo. A partir dos
valores de H(t) e t foi determinado, para cada ensaio, através de regressão linear, o valor do parâmetro a.
A validade da determinação proposta pode ser comprovada se este valor mantém-se constante ao longo
dos ensaios, demonstrando ser um característica invariável do meio filtrante utilizado.
RESULTADOS E DISCUSSÃO
Foram considerados os resultados de 23 ensaios com os filtros de taxa constante , enquanto o SFTD teve
os dados analisados para um total de 24 ciclos. Os dados de interesse constaram basicamente da variação,
ao longo do tempo, das perdas de carga totais e da turbidez do afluente e dos efluentes.
Os primeiros 21 ensaios com os filtros de taxa constante utilizaram a medição da turbidez em aparelho de
bancada. Os principais dados são apresentados na Tabela 1. Excetuando-se 6 ensaios, cujos resultados
foram descartados por problemas experimentais, obteve-se um valor médio de a1 = 0,00057 UT-1 , com
um desvio padrão s = 0,00005 e um coeficiente de variação c.v. = 9,6 %.
Tabela 1 - Dados dos ensaios com taxa constante e turbidez
medida no turbidímetro de bancada.
Ensaio
Taxa (m/d)
Ho (m)
Co (UT)
a (UT-1)
1
2
3
4
5
7
8
10
11
12
13
18
19
20
21
Média
300
500
600
550
450
400
200
550
550
450
450
250
350
250
350
-
0,31
0,55
0,65
0,62
0,45
0,44
0,19
0,61
0,61
0,45
0,51
0,27
0,40
0,26
0,41
.
2,56
2,56
2,50
2,50
2,50
2,38
2,38
2,20
2,20
2,20
2,20
2,38
2,38
2,38
2,38
-
0,00060
0,00055
0,00050
0,00048
0,00048
0,00065
0,00060
0,00065
0,00055
0,00060
0,00062
0,00058
0,00055
0,00053
0,00060
0,00057
Já para os 8 últimos ensaios, nos quais foram empregados os turbidímetros de escoamento contínuo e
cujos resultados aparecem na Tabela 2, a média calculada foi a2 = 0,00102 UT-1 , com s = 0,00004 e
c.v. = 4,1 %.
Para os ensaios com o SFTD, quando também foi empregada a medição contínua de turbidez e cujos
dados constam da Tabela 3, resultaram as seguintes valores médios de a para cada uma das três taxas de
filtração:
a) Ensaio 1 (taxa média de 250 m/d): a3 = 0,00107 UT -1 (s = 0,00020, c.v. = 18,9 %);
b) Ensaio 2 (taxa média de 300 m/d): a4 = 0,00102 UT -1 (s = 0,00018, c.v. = 17,5 %) e
c) Ensaio 3 (taxa média de 350 m/d) : a5 = 0,00113 UT -1 (s = 0,00018, c.v. = 15,8 %).
Tabela 2 - Dados dos ensaios com taxa constante e turbidez
medida no equipamento de escoamento contínuo.
Ensaio
Taxa (m/d)
Ho (m)
Co (UT)
a (UT-1)
25
26
27
29
30
31
32
33
Mádia
550
600
500
450
400
200
300
250
-
0,73
0,81
0,69
0,61
0,54
0,23
0,37
0,31
-
1,74
1,51
1,51
1,64
1,64
1,58
1,58
1,58
-
0,00106
0,00103
0,00108
0,00098
0,00098
0,00106
0,00096
0,00103
0,00102
Tabela 3 - Dados dos ensaios com o SFTD e turbidez
medida no equipamento de escoamento contínuo.
Ensaio
Ciclo
Ho (m)
Hf (m)
Taxa (m/d)
t (h)
Co (UT)
a (UT-1)
1
17
26
33
35
38
42
43
47
48
52
53
54
9
10
12
16
18
20
4
5
7
8
9
12
-
0,90
0,88
0,91
0,91
0,91
0,90
0,90
0,89
0,90
0,89
0,89
0,89
0,90
1,33
1,34
1,32
1,32
1,32
1,34
1,33
1,25
1,24
1,22
1,21
1,24
1,25
1,23
1,20
1,20
1,20
1,20
1,20
1,20
1,20
1,20
1,20
1,18
1,20
1,20
1,20
1,63
1,67
1,60
1,60
1,60
1,61
1,61
1,60
1,61
1,60
1,61
1,61
1,65
1,61
354
360
360
360
360
358
350
354
359
358
361
356
357
454
460
441
441
446
441
447
417
414
407
402
399
413
409
11,0
9,8
11,0
10,5
11,3
12,5
11,5
12,5
11,0
11,0
11,0
12,0
11,3
8,0
8,0
7,5
8,0
6,5
7,5
7,6
10,3
8,8
9,2
11,2
11,0
9,5
10,0
1,84
2,21
1,97
2,87
1,68
1,68
1,40
1,42
1,84
1,50
1,31
1,49
1,77
2,14
2,51
2,25
1,73
2,29
1,44
2,06
1,81
1,95
1,73
2,34
1,90
2,21
1,99
0,00103
0,00098
0,00091
0,00065
0,00103
0,00098
0,00130
0,00118
0,00098
0,00118
0,00144
0,00118
0,00107
0,00091
0,00086
0,00091
0,00110
0,00101
0,00134
0,00102
0,00110
0,00125
0,00142
0,00089
0,00106
0,00110
0,00113
Média
2
Média
3
Média
É importante observar que o valor da taxa de filtração utilizado no cálculo do coeficiente a, conforme
mostrado na Tabela 3, é o valor da taxa máxima registrada no filtro mais limpo do SFTD, de acordo com as
conclusões obtidas por DI BERNARDO & TEIXEIRA (1992).
Embora apresentando uma dispersão relativamente maior em relação à média, tais valores do parâmetro a
estão bastante próximos do valor a2. Uma análise estatística mais rigorosa mostrou que, num nível de
significância de 5%, os mesmos não diferiram entre si. Calculando-se um valor médio a partir de todos os
dados válidos de ensaios com turbidímetros contínuos, obteve-se a = 0,00106 UT -1 (s = 0,00016, c.v. =
15,5%).
A mudança do equipamento para medição de turbidez acarretou, sem dúvida, uma alteração significativa
no cálculo do parâmetro a. Os próprios valores de turbidez medida diferiram
entre si, com os
equipamentos de escoamento contínuo apresentando leituras consistentemente menores que o aparelho de
bancada, ambos calibrados segundo as instruções do fabricante, por sinal o mesmo. Estas diferenças
constituem-se numa limitação ao método de determinação aqui estudado, não se podendo comparar
valores calculados a partir de turbidímetros diferentes.
Independentemente deste fato, que reflete uma situação particular que deve ser evitada, pode-se
questionar o uso da turbidez como o parâmetro ideal para representar a quantidade (e, principalmente, o
tipo) de partículas presentes no afluente ao filtro. É provável que as variações numéricas nos valores de
turbidez não acompanhem proporcionalmente as variações do número de partículas. Este argumento é
reforçado pelo fato de que, em ensaios onde os valores da turbidez média do afluente eram
aproximadamente iguais, os valores do coeficiente a também resultaram próximos. De modo geral, os
ensaios realizados simultaneamente também apresenteram resultados semelhantes. Em ambos os casos, a
limitação imposta pela utilização da turbidez nos cálculos deixou de ser significativa. Conceitualmente,
inclusive, não seria correto utilizar valores de turbidez em cálculos, mesmo no cálculo de uma “ turbidez
média” , a qual, estritamente falando, não tem significado.
Apesar destas limitações, o fato dos valores médios não diferirem significativamente entre si demonstra
que o coeficiente a reflete, da forma como foi calculado, o comportamento da perda de carga ao longo dos
ensaios, caracterizando o meio filtrante estudado e podendo ser útil na determinação de outros prâmetros
de interesse. As limitações decorrentes do emprego da turbidez são compensadas pela facilidade na sua
obtenção, embora suas variações não devam ser muito acentuadas.
Uma aplicação para o coeficiente a é, por exemplo, a determinação do tempo de duração da carreira de
filtração, a partir da fixação de uma carga hidráulica máxima. Invertendo-se a eq. (1), o tempo é calculado
por:
t = ( Hf - Ho) / ( a.Co.v )
onde:
( 2)
Hf = carga hidráulica máxima (L).
Tal procedimento foi aplicado aos dados experimentais dos ensaios com o SFTD, tendo resultado valores
muito próximos entre os tempos calculados ( t2 ) e os tempos médios dos ciclos de operação registrados
em cada um dos ensaios ( t1), conforme mostrado na Tabela 4. Os valores de Hf, Ho, Co e v (este último
correspondente à taxa máxima de filtração, conforme já mencionado), assim como o de t1, correspondem
às médias dos respectivos ensaios, já tendo sido apresentados na Tabela 3. O valor de a utilizado para o
cálculo de t2 foi a média total de todos os ciclos experimentais considerados na operação com o SFTD.
Como consideração final, deve-se destacar que outras formulações para o cálculo do coeficiente a,
incluindo o parâmetro de qualidade do efluente ( C ), apresentaram resultados piores. Assim, a proposta
originalmente feita por IVES (1963), expressa na eq. (1), mostrou-se a mais adequada.
Tabela 4 - Comparação entre os tempos calculados (t1) e observados (t2)
para a duração dos ciclos de filtração no SFTD experimental
Ensaio
Hf (m)
Ho (m)
v (m/d)
Co (UT)
a (UT-1)
t1 (h)
t2 (h)
1
2
3
1,20
1,61
1,61
0,89
1,32
1,23
354
437
407
1,77
2,06
1,99
0,00106
0,00106
0,00106
11,25
7,58
10,00
11,20
7,29
10,62
CONCLUSÃO
Como conclusão final, pode-se considerar que a determinação de um coeficiente de variação de perda de
carga através da equação H(t) = Ho + a.Co.v.t , com o parâmetro Co representado pela turbidez do
afluente, levou a resultados razoáveis, principalmente quando não ocorreram diferenças significativas no
referido parâmetro de qualidade da água. Este mostrou-se, entretanto, o mais sujeito a causar imprecisões
quando do cálculo de a por meio daquela equação. Entretanto, devido à facilidade de medição, a turbidez,
desde que obtida em condições bem definidas e controladas, pode ser empregada na determinação do
coeficiente a. Maiores investigações e tentativas com outros parâmetros (sólidos suspensos, número de
partículas etc.) são recomendáveis.
REFERÊNCIAS
DI BERNARDO, L. & TEIXEIRA, B.A.N. (1992) Previsão de Duração de Carreira de Filtração em Sistemas
de Filtração com Taxa Declinante. Anais. XXIII Congreso de la Asociacion Interamericana de Ingenieria
Sanitaria y Ambiental, 1992. La Habana, Cuba, p. 665-679.
IVES, K.J. (1963) Simplified Rational Analysis of Filter Behaviour. Proc. Instn. Civ. Engrs. v. 25, p. 345364.
TEIXEIRA, B.A.N. (1991) Proposição de um Método para Obtenção de Parâmetros de Projeto e Operação
de Sistemas de Filtração com Taxa Declinante. Tese de Doutoramento. Escola de Engenharia de São
Carlos, Universidade de São Paulo. São Carlos, Brasil.
AGRADECIMENTOS
O autor deseja expressar seus agradecimentos ao Prof. Dr. Luiz Di Bernardo, da Escola de Engenharia de
São Carlos/USP, pela orientação da Tese de Doutoramento cujos dados deram origem ao presente
trabalho.