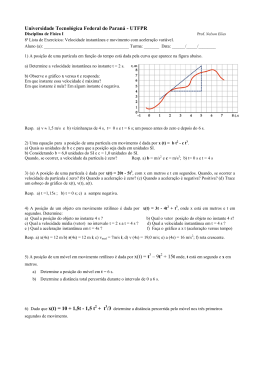
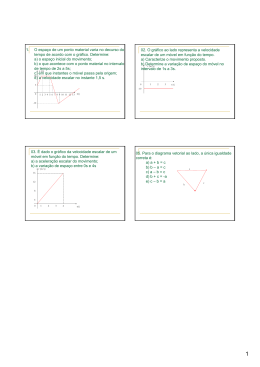
Parte B Física
1- Movimento a uma dimensão
1– Considere o gráﬁco da ﬁgura a seguir, que representa a função v(t), relativa a um dado
movimento rectilineo.
v (m s−1 )
30
1.1 – Qual o valor da velocidade inicial do móvel?
20
1.2 – Qual o escalar da aceleração do móvel?
10
1.3 – Determine, por meio do gráﬁco, o espaço per0
1
2
3 t (s)
corrido pelo móvel durante os 3 s iniciais?
−10
−20
30 m s−1
−15 m s−2
37.5 m
2– Considere o gráﬁco da ﬁgura a seguir, que representa a função v(t), relativa a um dado
movimento rectilineo.
2.1 – Qual o valor da velocidade inicial do móvel?
2.2 – Determine o(s) instante(s) em que o móvel ini- v
ciou inversão do sentido de marcha.
2.3 – Determine o(s) intervalo(s) de tempo em que o
móvel esteve parado.
2.4 – Determine o(s) intervalo(s) de tempo em que a
aceleração do móvel foi nula.
2.5 – Determine, por meio do gráﬁco, o espaço percorrido pelo móvel durante os 4 s iniciais?
0 m s−1
(m s−1 )
10
5
0
2
−5
4
6
8
t (s)
−10
27.5 m
3– Considere o gráﬁco da ﬁgura a seguir, que representa a função v(t), relativa a um dado
movimento rectilineo. Determine:
3.1 – a aceleração do móvel nos intervalos de tempo
[0 ; 2] s, [2 ; 3] s, [5 ; 6] s, [7 ; 9] s, [9 ; 11] s e [11
; 12] s;
3.2 – o espaço percorrido e a velocidade média do móvel durante os 7 s iniciais;
3.3 – o espaço percorrido e a velocidade média do móvel durante os 5 s ﬁnais;
3.4 – o espaço percorrido e a velocidade média do móvel no deslocamento total efectuado.
3.5 – Admitindo que o móvel partiu da origem, determine a posição do móvel ao ﬁm dos 12 s de
movimento.
10
v (m s−1 )
10
35 m ; 5 m s−1
5
0
−5
−10
8 10 12
2 4 6
35 m ; 7 m s−1
t (s)
70 m ; 5.8 m s−1
0m
4– Um automóvel está a deslocar-se de leste para oeste. Será possível que tenha uma velocidade orientada para oeste e simultaneamente uma aceleração orientada para leste? Em
que circunstâncias?
5– Uma professora de física sai de casa e dirige-se a pé para o campus. Após 5 min começa
a chover e ela retorna a casa. A sua distância à casa em função do tempo é indicada pelo
gráﬁco da ﬁgura. Indique em qual dos pontos indicados no gráﬁco a velocidade é:
5.1 – zero;
5.2 – constante e positiva;
5.3 – constante e negativa;
5.4 – crescente em módulo;
5.5 – decrescente em módulo.
6– A ﬁgura seguinte mostra a velocidade em função do tempo para um carro movido a energia
solar. O motorista acelera desde a partida, deslocando-se depois durante 20 s com velocidade constante de 60 km h−1, e de seguida trava, parando 40 s após a partida. Determine a
sua aceleração média para os seguintes intervalos de tempo:
6.1 – de t = 0 s até t = 10 s;
6.2 – de t = 30 s até t = 40 s;
6.3 – de t = 10 s até t = 30 s;
6.4 – de t = 0 s até t = 40 s.
7– Uma partícula, inicialmente em repouso e na origem de uma trajectória rectilínea, move-se
com aceleração constante igual a 5 m s−2.
7.1 – Escreva a expressão da lei das velocidades do referido movimento. Trace o gráﬁco
correspondente a essa função.
v=5 t
7.2 – Escreva a expressão da lei horária e represente-a graﬁcamente.
x=2.5 t2
7.3 – Calcule a velocidade do móvel quando a sua posição é x = 10 m.
v=10 m s−1
8– Uma partícula desloca-se sobre uma recta e inicia o seu movimento a partir de um ponto
que se situa a −2 m da origem. No instante inicial o móvel apresenta uma velocidade
escalar de 3 m s−1 e move-se com a aceleração escalar constante de −1 m s−2.
8.1 – Escreva as expressões que traduzem as funções x(t) e v(t).
x=−2+3t−0.5t2
v=3−t
8.2 – Trace os gráﬁcos correspondentes às funções referidas em 8.1.
8.3 – Determine o(s) instante(s) em que a partícula passou pela origem.
√
3± 5
8.4 – Determine a posição da partícula quando a sua velocidade é nula.
2.5 m
11
9– Uma bicicleta desloca-se a 18 km h−1. Na posição 0 m o ciclista trava durante 10 s com
uma aceleração constante até parar. Determine:
9.1 – a aceleração da bicicleta;
a=−0.5 m s−2
9.2 – a distância percorrida pela bicicleta até parar;
25 m
9.3 – a posição da bicicleta no instante 8 s;
24 m
9.4 – a velocidade da bicicleta quando a mesma se encontra na posição 9 m.
v=4 m s−1
10– Um comboio desloca-se com a velocidade de 180 km h−1. O maquinista começa a reduzir
uniformemente a velocidade de modo a passar na estação seguinte com a velocidade de
45 km h−1, sendo a duração da travagem de 25 s. Calcule:
10.1 – o escalar da aceleração durante a travagem;
a=−1.5 m s−2
10.2 – o percurso efectuado pelo comboio durante a travagem.
∆x=781.25 m
11– Uma partícula desloca-se com um movimento que pode considerar-se resultante da composição de dois movimentos simultâneos e independentes: um, uniformemente acelerado
ao longo do eixo dos xx; outro, uniforme ao longo do eixo dos yy.
Uma lei possível para descrever o movimento desta partícula pode ser traduzido pela equação:
11.1 – ~r = 2.0 t2 êx + 1.0 êy
11.2 – ~r = 1.0 t2 êx − 2.0 t êy
11.3 – ~r = 1.0 t êx + 1.0 t2 êy
11.4 – ~r = 2.0 êx + 2.0 t2 êy
11.5 – ~r = 2.0 t êx + 1.0 t êy
alínea 11.2
12
2- Movimento de projecteis
1– Num jogo de basquetebol, a bola foi lançada de uma distância horizontal de 8 m do cesto.
Sabendo que o aro se encontrava 1.2 m acima da posição de lançamento da bola e que esta
esteve no ar durante 1.6 s até encestar, calcule:
1.1 – o ângulo formado pela direcção da velocidade da bola com a horizontal, no instante
de lançamento;
g=9.8 m s−2
1.2 – o instante em que a bola atingiu a altura máxima.
t∼0.88 s
θ0 ∼60°
2– Deixa-se cair do alto de um prédio uma pedra que chega ao solo após 3 s.
2.1 – Calcule, desprezando a resistência do ar:
2.1.1 – a altura do prédio
2.1.2 – a velocidade com que a pedra chega ao solo.
g=9.8 m s−2
h=44.1 m
v=29.4 m s−1
2.2 – Os resultados da alínea anterior seriam alterados se tivesse sido usado uma pedra
maior? Justiﬁque a sua resposta.
3– Com a mão a 1 m do solo um rapaz lança ao ar uma bola que atinge, relativamente ao solo,
a altura de 4 m. Considere g = 10 m s−2.
3.1 – Determine a velocidade com que a bola foi lançada.
v=7.75 m s−1
3.2 – Calcule o intervalo de tempo que decorreu entre o instante em que a bola foi lançada
e o instante em que a mesma tocou o solo.
∆t=1.67 s
4– Um avião, voando horizontalmente a 180 m de altitude, precisa de largar um saco com
mantimentos no centro de uma povoação. O módulo da sua velocidade é constante e igual
a 100 m s−1.
4.1 – A que distância do centro da povoação terá de situar-se a vertical que passa pelo
ponto de lançamento?
∆x=600 m
4.2 – Com que velocidade chega o saco ao solo?
v∼117 m s−1
5– Uma raqueta bate numa bola de ténis a 0.50 m do chão, comunicando-lhe uma velocidade
de 20 m s−1 segundo um ângulo de 15° com a horizontal. A bola move-se num plano perpendicular à rede, a qual tem 1.0 m de altura e se encontra a 20 m do ponto de lançamento.
Veriﬁque se a bola passa ou não por cima da rede.
13
não passa
6– Um jogador de futebol chuta, de uma altura de 20 cm, uma bola com uma velocidade de
20 m s−1 fazendo um ângulo de 60° com a horizontal, em direcção a uma baliza cuja barra
está a 2.3 m de altura. A distância do jogador à boca da baliza é de 30 m.
Veriﬁque se há golo.
não há golo
7– Numa competição, uma motorizada depara-se com um fosso de 12 m de largura. Para
possibilitar o salto há, antes do fosso, uma rampa com a inclinação de 20°.
7.1 – Qual deverá ser a velocidade mínima da motorizada, no ﬁnal da rampa, para saltar
uma distância de 12 m, necessária para ultrapassar o fosso?
v∼14 m s−1
7.2 – Discutir a validade do resultado obtido na alínea anterior, tendo em conta as aproximações efectuadas na sua resolução.
8– O tiro com ﬂechas e arco é um desporto conhecido desde o século XII a.C. Para que uma
ﬂecha tenha um alcance máximo deve ser lançada com um ângulo de 45° (desprezando a
resistência do ar). Este é o ângulo para o qual os valores das componentes horizontal e
vertical da velocidade inicial são iguais.
Supondo que se atira uma ﬂecha com uma velocidade inicial de 50 m s−1 com os seguintes
ângulos:
i) 30°; ii) 45°; iii)60°,
e admitindo que a ﬂecha é atirada ao nível do chão, determinar para cada caso:
v0x =v0 cos θ0
8.1 – as componentes horizontal e vertical da velocidade de lançamento;
v0y =v0 sin θ0
8.2 – o tempo que a ﬂecha permanece no ar, evidenciando na expressão resultante a componente vertical da velocidade;
t=2v0y /g
8.3 – o alcance da ﬂecha, evidenciando na expressão resultante a componente horizontal
da velocidade.
xmax =v0x tvoo
8.4 – Que conclusões se podem tirar dos resultados obtidos nas alíneas anteriores?
8.5 – Elaborar um texto em que se expliquem as razões pelas quais o alcance é máximo
para um ângulo de lançamento igual a 45°.
14
3- Movimento circular
1– Uma partícula animada de movimento circular e uniforme percorre um quarto de circunferência em 2.0 s. Determine para esta partícula:
1.1 – a frequência;
f =0.125 s−1
1.2 – a velocidade angular.
ω=π/4 rad s−1
2– Uma roldana de raio 0.20 m executa 120 rotações por minuto. Relativamente a um ponto
da periferia, determine:
2.1 – o período;
P=0.5 s
2.2 – a velocidade angular;
ω=4π rad s−1
2.3 – a velocidade linear.
v=2.51 m s−1
3– Numa pista circular de raio 100 m, um ciclista executa meia volta em 25 s, a velocidade
constante. Para o movimento do ciclista, determine:
3.1 – o período;
P=50 s
3.2 – a frequência;
f =0.02 s−1
3.3 – a velocidade linear;
v=4π m s−1
3.4 – a aceleração centrípeta.
ac ∼1.6 m s−2
4– Um ponto material desloca-se sobre um arco de circunferência de raio 600 m, com velocidade linear de 30 m s−1. Determine:
4.1 – a velocidade angular do móvel;
ω=0.05 rad s−1
4.2 – a aceleração centrípeta de que o móvel está animado.
ac =1.5 m s−2
5– Uma partícula percorre uma trajectória circular de raio igual a 4.0 m. Os valores das
velocidades nas posições A, B e C são, respectivamente: vA = 3.0 m s−1, vB = 4.0 m s−1 e
vC = 5.0 m s−1.
y
5.1 – Escreva as expressões do vector velocidade em A, B e
C.
B
~vB
~vA =(0,3) m s−1
x
0
30°
~vA
A
5.2 – Escreva a expressão do vector deslocamento entre as
posições A e C.
5.3 – Determine a aceleração média do movimento entre B
e C sabendo que a partícula demora 3.0 s a percorrer
essa distância.
15
~vB =(−3.46,−2) m s−1
~vC =(5,0) m s−1
∆~r=(−4,−4) m
C
~vC
~amed =(2.82,0.67) m s−2
6– Uma partícula material descreve uma trajectória circular de raio 4.0 m. A equação escalar
do movimento sobre a trajectória é:
s(t) = 3.0 t2 − 6.0 t + 1.0
(SI)
6.1 – Caracterizar, justiﬁcando, este movimento.
m.circ.u.a.
6.2 – Determinar o módulo da aceleração no instante t = 3.0 s.
a∼36.5 m s−2
7– Um ciclista desloca-se de A até B segundo o sentido representado na ﬁgura. O raio da
trajectória é de 2.0 m. A norma da aceleração em B é de 10.0 m s−2. Determine:
A
7.1 – Os vectores de posição em A e em B, considerando
como origem do referencial o centro da trajectória e
eixos ortonormados;
0
~a
7.2 – A aceleração normal em B;
37°
7.3 – O valor da velocidade em B;
~v
7.4 – O valor da aceleração tangencial em B.
B
~rA =(0,2)
~rB =(−1.2,−1.6)
an =7.99 m s−2
v=4 m s−1
at =6 m s−2
8– A lei do movimento de uma partícula material é dada pela expressão:
~r(t) = (2.0 t − 4.0) êx − (t2 − 4.0) êy
SI
8.1 – Determine a equação da trajectória.
y=−2 x−x2 /4
8.2 – Determine, para o instante t = 2.0 s:
8.2.1 – a velocidade da partícula;
8.2.2 – a aceleração tangencial da partícula;
8.2.3 – o raio da trajectória.
~v=(2,−4) m s−1
at =1.79 m s−2
R=22.5 m
9– As três partículas A, B e C têm trajectórias circulares de raio 5.0 m, sendo |~a| = 20 m s−2.
No instante inicial têm, respectivamente, as velocidades ~vA , ~vB e ~vC indicadas na ﬁgura.
~vA
0
~a
30°
A
~vC
~vB
135°
0
B
0
~a
C
~a
|~vA |=9.3 m s−1
|~vB |=8.4 m s−1
9.1 – Calcule |~vA |, |~vB | e |~vC |.
|~vC |=10 m s−1
9.2 – Calcule o valor de at em cada caso.
9.3 – Caracterize cada um dos movimentos no instante inicial.
16
10m s−2 ;14m s−2 ;0m s−2