1.
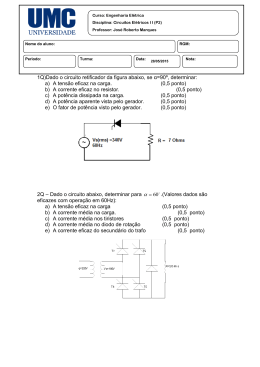
Seja o retificador mostrado abaixo, onde V1(ωt)=220sen(wt); R= 20Ω e L=100mH; f=50Hz.
Calcular VLmed, ILmed.e o FP da estrutura.
D1
R
V1(ωt)
L
Solução:
Cálculo do ângulo de extinção de corrente β:
(1.1)
(1.2)
√
[
(
)]
[
(
)]
(1.3)
Através do ábaco de Puschlowski obtêm-se com:
α=0
a= 0
cosΦ=0,4
β=254°
cosΦ=0,6
β=236°
Fazendo uma média obtêm-se
α=0
a= 0
cosΦ=0,55
(1.4)
β=240,5°
Cálculo do ângulo crítico de extinção de corrente βc:
(1.5)
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
Para este circuito tem-se α=0 e m=1.
Βc=360°
(1.6)
Como β< βc , é condução descontínua.
Cálculo da tensão média na carga VLmed:
(
∫√
)
(1.7)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução e β é o ângulo de fim de
condução do diodo.
∫
(
)
(1.8)
Cálculo da corrente média na carga ILmed:
(1.9)
Cálculo do fator de potência:
Para o cálculo do fator de potência é necessário o valor da corrente eficaz na carga e na fonte de tensão,
que neste caso é o mesmo para os dois.
1
Sendo
(
)
(
)
(1.10)
Utilizando o ábaco da Fig.2.8 do livro de Eletrônica de Potência 6ª edição de Ivo Barbi para correntes
normalizadas obtêm-se:
Ief=0,63A
(1.11)
Portanto:
√
(
)
(1.12)
√
(1.13)
Potência dissipada na carga:
P=R·ILef2
(1.14)
P=20·3,72²=276,77 W
(1.15)
S=Vef·Ief
(1.16)
S=155,56·3,72=578,68 VA
(1.17)
Potência aparente na fonte:
(1.18)
2.
Considere o conversor abaixo onde V(ωt)=220sen(ωt)
E=120V; L=100mH; R=8Ω; f= 50Hz
D
1
R
L
V(ωt)
E
a)
Calcule o ângulo de extinção da corrente e defina o modo de condução.
b)
Apresente as formas de onda e calcule VLmed e ILmed..
c)
Sendo E=0V e R= 20Ω, dicione em nti-paralelo com a carga um diodo e calcule o valor da
indutância para se obter condução crítica.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
Devido a presença de fonte E na carga o ângulo de início de condução do diodo deix de ser α=0° e
passa a ser o ângulo θ1 em que a fonte de entrada tem seu valor igual ao da fonte E, onde a partir desse
momento polarizando positivamente o diodo dando início a condução.
P r determin r o ângulo θ1 deve se igu l r
inst nte ωt= θ1.
tensão E com
220·sen(ωt)=120
α= Θ1 = ωt = 33,05°=0,576 rad
tensão de entr d e isol r ωt, pois neste
(2.1)
2
(2.2)
√
[
(
)]
[
(
)]
(2.3)
Através do ábaco de Puschlowski e fazendo médias sucessivas obtêm-se:
cos   0, 2
α=33,05°
a= 0,4

cos   0, 4 
cos   0,3

cos   0, 25 
 221

cos   0, 4 
cos   0,3

cos   0, 25 
 194
cos   0, 2
α=33,05°
a= 0,6
 210
 215,5
 218, 25
 187
 190,5
(2.4)
 192, 25
Fazendo uma média obtêm-se
a= 0,5
cos   0, 25   205, 25
a= 0,55 cos   0, 25
  198,75  3, 47rad
Cálculo do ângulo crítico de extinção de corrente βc:
(2.5)
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
Para este circuito monofásico de meia onda tem-se m=1 e α= 33,05° logo,
βc=360+33,05=393,05°
(2.6)
Como β< βc tem-se condução descontínua.
b)
Formas de onda
V(ωt)
400V
200V
0
V
-200V
-400V
400V
VL
200V
0
V
-200V
-400V
400V
VD1
200V
0
V
-200V
-400V
4.0A
IL
2.0A
0A
0
π
2π
3π
4π
3
Cálculo da tensão média na carga VLmed:
(
∫√
)
∫
(2.7)
Onde n é o número de pulsos do conversor,θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo (extinção d corrente β) e θ3 é o ângulo de reinício de condução do diodo.
(
∫
)
∫
(2.8)
Cálculo da corrente média na carga ILmed:
(2.9)
c)
Indutância necessária para condução critica Lc:
Colocando um diodo em anti-paralelo, torna-se o circuito em um circuito monofásico de meia onda com
roda livre, onde para que haja condução critica é necessário que
(2.10)
Onde π é o ângulo em que se tem roda livre, ou seja, é o tempo em que o indutor se descarregará
através do resistor até a fonte de entrada voltar a carregar o indutor. ω é freqüênci ngul r e τ é const nte
de tempo do circuito dada por L/R.
Portanto para que haja condução contínua é necessário que o tempo de 5τ sej m ior que o tempo em
que a fonte fica sem fornecer energia à carga. Logo.
(2.11)
3.
Para o retificador monofásico de onda completa com ponto médio abaixo.
R=2Ω; L=3mH; E=36V; V(ωt)=180sen(ωt); f=50Hz; rt=10mΩ; Vto=1V; Ta= 50°C; N1/N2=3
D
1
R
N
2
V(ωt)
L
N
1
N
2
E
D
2
a)
b)
c)
C lcul r o ângulo de extinção d corrente, βc e definir o modo de condução.
Traçar as formas de onda.
Calcular VLmed, ILmed.e, se possível ILef.
Solução:
Sendo N1/N2=3 a tensão nas bobinas do transformador no secundário é V2(ωt)=60sen(ωt).
a)
Cálculo do ângulo de extinção de corrente β:
Devido a presença de fonte E na carga o ângulo de início de condução do diodo deixa de ser α=0° e
passa a ser o ângulo θ1 em que a fonte de entrada tem seu valor igual ao da fonte E, onde a partir desse
momento polarizando positivamente o diodo dando início a condução.
4
P r determin r o ângulo θ1 deve se igu l r
inst nte ωt= θ1.
tensão E com
tensão de entr d e isol r ωt, pois neste
60·sen(ωt)=36
=Θ1 = ωt = 36,87°=0,644 rad
(3.1)
(3.2)
√
[
(
)]
[
(
)]
(3.3)
Através do ábaco de Puschlowski obtêm-se:
a=0,6
cosΦ=0,9
(3.4)
β=164° ou 2,862 r d
Cálculo do ângulo crítico de extinção de corrente βc:
(3.5)
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
Para circuito monofásico de ponto médio, m=2 e α=36,87°.
Logo,
βc=180+36,87°=216,87°
(3.6)
Como β< βc tem-se condução descontínua.
b)
Formas de onda
V(ωt)
100V
0V
-100V
100V
VL
50V
0V
0V
VD1
-100V
-200V
10.0A
IL
5.0A
0A
c)
0
3π
2π
π
4π
Cálculo da tensão média na carga VLmed:
∫√
(
)
∫
(3.7)
5
Onde n é o número de pulsos do conversor,θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo (extinção d corrente β) e θ3 o ângulo de reinício de condução do diodo.
(
∫
)
∫
(3.8)
Cálculo da corrente média na carga ILmed:
(3.9)
Cálculo da corrente eficaz na carga ILef:
Como a condução é descontínua, as harmônicas de ordem superior não podem ser desprezadas e o
cálculo se torna muito complexo.
4.
Considere o circuito abaixo.
V(ωt)=√ 220sen(ωt); f= 60Hz; R=20Ω; E=60V.
D1
D2
R
V(ωt)
D5
D3
E
D4
a)
Tr ç r s form s de ond V(ωt), VL(ωt), IL(ωt) e VD1.
b)
Calcule o valor da tensão média, corrente média e da corrente eficaz na carga.
c)
Calcular o valor da resistência térmica entre junção e o ambiente para que o diodo D5 se
mantenha com uma temperatura de junção de 150°C
Solução:
Analisando o circuito, vê-se que o diodo D5 nunca entrará em condução, pois como não se tem
indutância no circuito, a menor tensão que aparecerá na carga será a da própria fonte E, polarizando
negativamente o diodo D5.
a)
Formas de onda:
Ângulo de inicio de condução θ1
P r determin r o ângulo θ1 deve se igu l r
inst nte ωt= θ1.
tensão E com
311·sen(ωt)=60
Θ1 = ωt = 11,12°=0,194 rad
tensão de entr d e isol r ωt, pois neste
(4.1)
6
V(ωt)
400V
0V
-400V
400V
VL
200V
0V
0V
VD1
-200V
-400V
20A
IL
10A
0A
b)
π
0
3π
2π
4π
Cálculo da tensão média na carga VLmed:
(
∫√
)
∫
(4.2)
Onde n é o número de pulsos do conversor,θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo (extinção d corrente β) e θ3 o ângulo de reinício de condução do diodo.
311·sen(ωt)=60
Θ1 = ωt = 11,12°=0,194 rad
(4.3)
Θ2=ωt=180-11,12=168,88°=2,948 rad
(4.4)
Θ3=π + 0,194 r d
(4.5)
∫
(
)
∫
(4.6)
Cálculo da corrente média na carga ILmed:
(4.7)
7
Cálculo da corrente eficaz na carga ILef:
√
∫(
(
√
)
)
(4.8)
√
c)
ambiente.
5.
(
∫ (
)
)
Como o diodo não entra em condução, a temperatura do diodo se mantém em temperatura
Considere o conversor abaixo com:
V(ωt)=√ 220sen(ωt); f= 60Hz; R=1Ω; L=1000mH; E=60V.
D1
D2
R
V(ωt)
L
D3
E
D4
a)
b)
c)
C lcul r o ângulo de extinção d corrente, βc e definir o modo de condução.
Tr ç r s form s de ond V(ωt), VL(ωt), IL(ωt) e VD1.
Calcule o valor da tensão média, corrente média e da corrente eficaz na carga.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
Devido a presença de fonte E na carga o ângulo de início de condução do diodo deix de ser α=0° e
passa a ser o ângulo θ1 em que a fonte de entrada tem seu valor igual ao da fonte E, onde a partir desse
momento polarizando positivamente o diodo dando início a condução.
P r determin r o ângulo θ1 deve se igu l r
inst nte ωt= θ1.
tensão de entr d e isol r ωt, pois neste
311·sen(ωt)=60
(5.1)
α =Θ1 = ωt = 11,12°=0,194 rad
(5.2)
√
[
tensão E com
(
(5.3)
√
)]
[
(
)]
(5.4)
Através do ábaco de Puschlowski se obtêm:
α=11,12°
a=0,2
cosΦ=0
β=274° ou 2,862 r d
(5.5)
Cálculo do ângulo crítico de extinção de corrente βc:
(5.6)
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
8
Para este circuito monofásico de onda completa tem-se m=2 e α=11,12°.
βc=180+11,12°=191,12°
(5.7)
Como β> βc tem-se condução contínua.
b)
Formas de onda
400V
V(ωt)
0V
-400V
400V
VL
0V
-400V
400V
VD1
0V
-400V
IL
150A
100A
50A
0A
c)
3π
2π
π
0
4π
Cálculo da tensão média na carga VLmed:
(
∫√
)
(5.8)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo e θ2 é o ângulo
de fim de condução do diodo.
∫
(
)
(5.9)
Cálculo da corrente média na carga ILmed:
(5.10)
9
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e β é m ior que βc o suficiente para considerar a corrente na carga uma
constante. Então:
(5.11)
6.
Considere o retificador trifásico com ponto médio da figura abaixo.
V1(ωt)=√ 220sen(ωt); V2(ωt)=√
L=3000mH; rt=11mΩ; Vto=1V; Ta=40°C.
220sen(ωt+120°); V3(ωt)=√
V1(ωt)
D1
V2(ωt)
D2
220sen(ωt-120°); f= 60Hz; R=5Ω;
R
V3(ωt)
D3
L
a)
Traçar as formas de onda V1, V2, V3, VL, IL e VD2.
b)
Calcular VLmed, ILmed, ILef, VD1, IDmed, IDef.
c)
Calcular o valor da resistência térmica entre junção e o ambiente para que o diodo D2 se
mantenha com uma temperatura de junção inferior à 150°C.
d)
Calcular o FP da fonte 2.
Solução:
a)
Formas de onda:
Cálculo do ângulo de extinção de corrente β:
α=30°.
(6.1)
(6.2)
√
[
(
)]
[
(
)]
(6.3)
Através do ábaco de Puschlowski obtêm-se:
α=30°
a= 0
cosΦ=0
β= 330°
(6.4)
Cálculo do ângulo crítico de extinção de corrente βc:
(6.5)
Para este circuito trifásico de ponto médio tem-se m=3 e α= 30° logo,
βc=120+30=150°
(6.6)
Como β> βc tem-se condução contínua.
10
V1(ωt)
V2(ωt)
V3(ωt)
400V
200V
0V
-200V
-400V
400V
VL
200V
0V
VD2
0V
-250V
-500V
100A
IL
50A
0A
b)
3π
2π
π
0
4π
Cálculo da tensão média na carga VLmed:
(
∫√
)
(6.7)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo.
∫
(
)
(6.8)
Cálculo da corrente média na carga ILmed:
(6.9)
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e β é m ior que βc o suficiente para considerar a corrente na carga uma
constante. Então:
(6.10)
11
Cálculo da tensão de pico de D1 VD1:
√
√
√
√
(6.11)
Cálculo da corrente média no diodo:
No circuito trifásico o diodo conduz em 1/3 do tempo total do ciclo. Então:
(6.12)
Cálculo da corrente eficaz no diodo:
√
c)
∫(
)
(6.13)
√
√
Resistência junção-ambiente:
Cálculo da potência dissipada em um diodo:
(6.14)
Cálculo da resistência junção-ambiente.
(6.15)
(6.16)
d)
Fator de potência:
(6.17)
Cálculo da potência ativa na carga:
(6.18)
A potência ativa na fonte pode ser dada pela potência ativa na carga pela quantidade de fontes
presentes no circuito.
(6.19)
Cálculo da potência aparente da fonte:
A potência aparente na fonte é dada pela tensão eficaz da fonte e pela corrente eficaz na fonte, que
neste caso é dado pela corrente eficaz no diodo.
(6.20)
Cálculo do fator de potência:
(6.21)
12
7.
Para o retificador trifásico com ponto médio da figura abaixo.
V1(ωt)=√ 220sen(ωt); V2(ωt)=√
L=26mH; E=124V.
220sen(ωt-120°); V3(ωt)=√
V1(ωt)
D1
V2(ωt)
D2
220sen(ωt+120°); f= 60Hz; R=2Ω;
R
V3(ωt)
D3
L
E
a)
b)
c)
Obtenha o ângulo de extinção da corrente, o ângulo crítico e determine o modo de condução.
Traçar as formas de onda VL(ωt), IL(ωt) e VD1.
Calcular VLmed, ILmed, ILef, VDp, IDmed, IDef.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
Devido a presença da fonte é necessário verificar se o ângulo em que a fonte de entrada torna-se maior
do que o do valor da fonte E é maior ou menor do que 30° a fim de verificar a influência da fonte E no início de
condução do diodo.
311·sen(ωt)=124
(7.1)
Θ1 = ωt = 23,50°
Como o ângulo em que a fonte de entrada ultrapassa o valor da fonte E é menor do que 30°(ângulo em
que uma fonte de entrada se torna a fonte com o maior valor de tensão do circuito forçando a condução do
diodo) se tem
α=30°.
√
[
(7.2)
(7.3)
√
(
)]
[
(
)]
(7.4)
Através do ábaco de Puschlowski e fazendo médias sucessivas obtêm-se:
α=30° a= 0,4
cosΦ=0,2
β= 221°
(7.5)
Cálculo do ângulo crítico de extinção de corrente βc:
(7.6)
Para este circuito trifásico de ponto médio, m=3 e α= 30° logo,
βc=120+30=150°
(7.7)
13
Como β>βc tem-se condução contínua.
b)
Formas de onda
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
400V
VL
200V
0V
VD1
0V
-250V
-500V
100A
IL
75A
50A
25A
0A
c)
3π
2π
π
0
4π
Cálculo da tensão média na carga VLmed:
(
∫√
)
(7.8)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo.
∫
(
)
(7.9)
Cálculo da corrente média na carga ILmed:
(7.10)
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e β é m ior que βc o suficiente para considerar a corrente na carga uma
constante. Então :
(7.11)
Cálculo da tensão de pico de D1 VD1:
14
√
√
√
√
(7.12)
Cálculo da corrente média no diodo:
No circuito trifásico o diodo conduz em 1/3 do tempo total do ciclo. Então:
(7.13)
Cálculo da corrente eficaz no diodo:
√
∫(
(7.14)
)
√
√
8.
Considere o conversor abaixo com tensão eficaz de linha de 440V, f=60Hz, Vto=0,5V e rt=8mΩ.
R=2Ω; L=100mH; E=350V;
D
1
V1(ωt
)
D
2
D
3
R
V2(ωt
)
L
V3(ωt
)
E
D
4
a)
b)
c)
d)
D
5
D
6
Calcular o ângulo de extinção da corrente, o ângulo crítico e determinar o modo de condução.
Traçar as formas de onda V1, V2, V3, VL, IL, ID1, VD1 e calcular VLmed, ILmed, IDmed, IDef
Calcular a potência dissipada e a tensão máxima em cada diodo.
Calcular o rendimento da estrutura e o FP.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
É necessário verificar se o ângulo em que a fonte de entrada torna-se maior do que o do valor da fonte E
é maior ou menor do que 60° a fim de verificar a influência da fonte E no início de condução do diodo.
622,25·sen(ωt)=350
(8.1)
Θ1 = ωt = 34,23°
Como o ângulo em que a fonte de entrada ultrapassa o valor da fonte E é menor do que 60°(ângulo em
que uma tensão de linha se torna a maior no circuito forçando a condução dos diodos) se tem:
α=60°.
√
[
(8.3)
√
√
(
(8.2)
)]
[
(
)]
(8.4)
Através do ábaco de Puschlowski e fazendo médias sucessivas obtêm-se:
15
α=60°
a= 0,6
cosΦ=0
β= 199°
(8.5)
Cálculo do ângulo crítico de extinção de corrente βc:
(8.6)
Para este circuito em ponte de Graetz, m=6 e α= 60° logo,
βc=60+60=120°
(8.7)
Como β>βc tem-se condução contínua.
b)
Formas de onda
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
VL
500V
250V
0V
0V
VD1
-250V
-500V
200A
IL
ID1
100A
-10A
c)
3π
2π
π
0
4π
Cálculo da tensão média na carga VLmed:
∫√
(
√
)
(8.8)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução de um par de diodos, θ2
é o ângulo de fim de condução do par de diodos.
∫
(
)
(8.9)
Cálculo da corrente média na carga ILmed:
16
(8.10)
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e β é m ior que βc o suficiente para considerar a corrente na carga uma
constante. Então:
(8.11)
Cálculo da tensão de pico de D1 VD1:
√
√
√
(8.12)
Cálculo da corrente média no diodo:
No circuito em ponte de Graetz cada diodo conduz em 1/3 do tempo total do ciclo. Então:
(8.13)
Cálculo da corrente eficaz no diodo:
√
d)
∫(
(8.14)
)
√
√
Cálculo do rendimento:
Para o cálculo do rendimento verifica-se potência entregue na carga pela potência entregue pelas
fontes(potência dissipada nos diodos e potência dissipada na carga)
(
)
(8.15)
(
)
Cálculo do fator de potência:
(8.16)
Cálculo da potência dissipada na carga:
(8.17)
Cálculo da potência aparente entregue pelas fontes
(8.18)
(8.19)
17
9.
Deseja-se utilizar o retificador com filtro capacitivo para alimentar um circuito CMOS,
sabendo que a variação de tensão admitida no circuito é de 14,6V à 15,4V e que a potência consumida é de
pelo menos 5W calcule:
V1(ωt)=311sen(ωt); f=50Hz.
a)
b)
Calcule C, R e Icef.
Calcule e especifique o transformador.
Solução:
a)
Considerando os valores de tensão admitidos no circuito tem-se a tensão de pico com 15,4V e
a tensão mínima de 14,6V. Assim
(9.1)
Pelo ábaco da figura 10.9 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi obtêm-se ωRC=48
Considerando que a tensão média no circuito seja de 15V e a potência de 5W, obtêm-se o valor da
resistência:
(9.2)
Assim
(9.3)
Pelo ábaco da figura 10.10 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi se obtêm
(9.4)
E a tensão máxima no capacitor é a tensão máxima de ondulação permitida no circuito:
Vpk=15,4V
(9.5)
b)
À partir do ábaco da figura 10.29 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi
obtêm-se FP=0,42. Logo
(9.6)
Tensão de saída do transformador:
A tensão de saída do transformador é obtida através do valor de pico necessário no circuito:
√
(9.7)
Tensão de entrada do transformador
A tensão de entrada do transformador é obtida através do valor da fonte de entrada do circuito.
√
(9.8)
18
10.
Para o retificador com filtro capacitivo da figura abaixo, onde:
V1(ωt)= √ 127sen(ωt); f=60Hz; R=10Ω.
D1
D2
V1(ωt)
C
R
D3
D4
a)
Calcular e especificar o capacitor (C) para que a máxima ondulação de tensão na carga seja de
10% da tensão de pico de entrada.
b)
Calcular a corrente eficaz neste capacitor.
c)
Qual o fator de potência da estrutura?
Solução:
a)
Cálculo do capacitor:
Para que a máxima tensão de ondulação seja de 10%, sendo o pico de 179,61V diminui-se 10% do valor
de pico da tensão de entrada da fonte para obter a mínima tensão no capacitor que é de 161,64V. Assim
(10.1)
Pelo ábaco da figura 10.9 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi obtêm-se ωRC=30.
Logo
(10.2)
b)
Corrente eficaz no capacitor:
Pelo ábaco da figura 10.10 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi obtêm-se
(10.3)
c)
FP=0,46
pelo ábaco da figura 10.29 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi obtêm-se
19
11.
Deseja-se usar o circuito como fonte de tensão média de 600V, dados
V1(ωt)=√ 220sen(ωt); V2(ωt)=√
Pout=600W. Considere transformador Y-Y
a)
b)
220sen(ωt-120°); V3(ωt)=√
220sen(ωt+120°); f= 60Hz; ∆Vo=2%;
Calcular e especificar o capacitor (capacitância, corrente eficaz e máxima tensão).
Calcular e especificar o transformador (tensão eficaz de entrada e saída e potência(VA))
Solução:
a)
Como se deseja uma tensão média de 600V e uma ondulação máxima de 2%, considera-se
que seja 1% acima e 1% abaixo. Logo
(11.1)
Cálculo da capacitância:
Pelo ábaco da figura 10.22 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi obtêm-se ωRC=35
A resistência da carga se obtêm através da seguinte expressão:
(11.2)
Logo
(11.3)
Cálculo da corrente no capacitor:
Pelo ábaco da figura 10.24 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi se obtêm
(11.4)
A tensão de pico do capacitor será tensão de pico estabelecida para a carga
Vpk=606V
b)
(11.5)
Cálculo do transformador
Através do ábaco da figura 10.34 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi se obtêm
FP=0,42
Assim a potência do transformador é obtida conforme a seguir
(11.6)
20
Cálculo da tensão de saída:
(11.7)
√ √
Cálculo da tensão de entrada
√
(11.8)
√
12.
Considere o retificador trifásico com ponto médio da figura abaixo. Sabe-se que o diodo D1
está queimado (aberto) e que:
V1(ωt)=√ 220sen(ωt); V2(ωt)=√ 220sen(ωt-120°); V3(ωt)=√ 220sen(ωt+120°); f= 60Hz; R=5Ω; L=3H;
D1=D2=D3=SKN 20/04, rt= 11mΩ, Vto=1V; Ta=40°C.
V1(ωt)
D1
V2(ωt)
D2
R
V3(ωt)
D3
L
a)
Traçar as formas de onda V1, V2, V3, VL, IL e VD2.
b)
Calcular VLmed, ILmed, ILef, VD2, IDmed, IDef.
c)
Calcular o valor da resistência térmica entre junção e o ambiente para que o diodo D2 se
mantenha com uma temperatura de junção inferior à 150°C.
Solução:
a)
Formas de onda
Verificação condução contínua
Devido a presença do diodo queimado verifica-se se o β possui um v lor de ângulo maior que o ângulo
em que o próximo diodo entre em condução, assim tendo condução continua. Em um sistema trifásico na
queima de um diodo a carga permanece com tensão negativa durante 60°. Logo é necessário que
β=180°+60°=240° p r que o proximo diodo entre em condução. assim
3 °
(12.1)
(12.2)
√
[
(
)]
[
(
)]
(12.3)
Através do ábaco de Puschlowski obtêm-se:
α=30° a= 0
cosΦ=0 β= 330°
(12.4)
Assim como β é m ior que 240°, é condução contínua
21
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
400V
VL
0V
-400V
VD2
0V
-250V
-500V
40A
IL
30A
20A
10A
0A
π
0
b)
3π
2π
4π
Cálculo da tensão média na carga VLmed:
(
∫√
)
(12.5)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo.
(
∫
)
(12.6)
Cálculo da corrente média na carga ILmed:
(12.7)
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, com 5τ maior que o tempo em que a carga é submetida a tensão negativa
o suficiente para considerar a corrente na carga uma constante. Então:
(12.8)
Cálculo da tensão de pico de D2 VD2:
√
√
√
√
(12.9)
Cálculo da corrente média no diodo:
Neste circuito cada diodo conduz em 1/2 do tempo total do ciclo. Então:
(12.10)
22
Cálculo da corrente eficaz no diodo:
√
c)
∫(
)
√
(12.11)
√
Resistência junção ambiente
Cálculo da potência dissipada no diodo:
(12.12)
Cálculo da resistência junção-ambiente:
(12.13)
d)
Cálculo do fator de potência:
(12.14)
Cálculo da potência ativa fornecida por cada fonte:
A potência que cada fonte fornece ao circuito é a potência total dissipada no resistor de carga dividida
pelo número de fontes que fornecem energia ao circuito, que neste circuito devido a queima de um diodo,
apenas duas fontes fornecem energia ao circuito.
(12.15)
Cálculo da potência aparente
(12.16)
(12.17)
13.
Considere o circuito abaixo, que se encontra com o diodo D1 queimado, com tensão eficaz de
linha de 380V.
R=2Ω; L=100mH; E=350V; f=60Hz;
V1(ωt
)
D1
D2
D3
R
V2(ωt
)
L
V3(ωt
)
E
D4
a)
b)
D5
D6
Traçar as formas de onda V1, V2, V3, VL, IL, ID2 e VD2.
Calcular VLmed, ILmed, ILef, ID2med, ID2ef.
23
Solução:
a)
Formas de onda
Devido a presença do diodo queimado verifica-se se o β possui um v lor de ângulo m ior que o ângulo
em que o próximo diodo entre em condução, assim tendo condução continua. Em ponte de Graetz RLE na
queima de um diodo a carga permanece com tensão menor que da fonte E dur nte 2.θ1, sendo θ1 o ângulo em
que fonte de tensão lev p r s ir de 0 e ir té o v lor d fonte E. logo é necessário que β= 180°+θ1. Assim:
537,4·sen(ωt)=350
Θ1 = ωt = 40,64°
(13.1)
β=180+40,64=220,64°
Assim o v lor de β terá que se m ior que 220,64°
60°
√
[
(
(13.2)
(13.3)
√
√
)]
[
(
)]
(13.4)
α=60° a= 0,65 cosΦ=0 β= 191°
(13.5)
Através do ábaco de Puschlowski obtêm-se:
Como β é menor que 220,64° poderi se firm r que seri condução descontínu , porém neste c so
pode se considerar contínua, devido ao fato que o ábaco de Puschlowski foi feito considerando que a carga em
um ângulo de condução superior a 180° estaria submetido a uma tensão negativa. Neste problema a tensão na
carga entre 180° e 220,64° permanece positiva, porém com um valor menor que da fonte E, mas não negativa.
Como a tensão na carga quando chega a 180° volta a subir, o indutor necessita criar uma tensão menor entre
seus terminais a fim de que a tensão de saída acompanhe a tensão de entrada. Com esta tensão menor o
indutor perm nece m is tempo c rreg do, ssim mesmo obtendo um β entre 180° e 220,64° pode se
considerar condução continua devido a este fenômeno.
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
VL
500V
250V
0V
0V
VD2
-250V
-500V
IL
100A
ID2
50A
0A
0
π
2π
3π
4π
24
b)
Cálculo da tensão média na carga VLmed:
(
∫√
)
(13.3)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o
ângulo de fim de condução do diodo.
Pode-se
(
∫
)
(
∫
)
(13.4)
Cálculo da corrente média na carga ILmed:
(13.5)
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e o tempo de 5τ é m ior o suficiente que o tempo em que as fontes de
entrada ficam com tensão menor que o da fonte E para considerar a corrente na carga uma constante. Então :
(13.6)
Cálculo da corrente de pico de D1 VD1:
√
√
√
(13.7)
Cálculo da corrente média no diodo:
Devido ao diodo queimado os diodos da parte superior conduzem em metade do período cada
enquanto os diodos da parte inferior conduzem um terço do periodo. Então:
Diodos superiores:
(13.8)
Diodos inferiores:
(13.9)
Cálculo da corrente eficaz no diodo:
Diodos superiores:
√
∫(
)
√
∫(
)
√
√
√
√
(13.10)
Diodos inferiores:
(13.11)
25
14.
Considere o conversor abaixo com:
V(ωt)=225sen(ωt); f=50Hz;R=2Ω; L=9mH; E=10V;N1/N2=9.
D1
R
N2
L
V(ωt)
N1
N2
E
D2
a)
b)
c)
d)
C lcul r o ângulo de extinção d corrente, βc e definir o modo de condução.
Tr ç r s form s de ond V(ωt), I(ωt), VL(ωt), IL(ωt) e ID1.
Calcule o valor da tensão média, corrente média e da corrente eficaz na carga.
A potência pode ser calculada por VLmed.ILmed? Justifique.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
Devido a presença de fonte E na carga o ângulo de início de condução do diodo deix de ser α=0° e
passa a ser o ângulo em que a fonte de entrada tem seu valor maior que o da fonte E, polarizando
positivamente o diodo dando início a condução.
25·sen(ωt)=10
α = Θ1 = ωt = 23,58°
(14.1)
(14.2)
√
[
(
)]
[
(
)]
(14.3)
Através do ábaco de Puschlowski obtêm-se:
α=23,58°
a= 0,4
cosΦ=0,6
β= 200°
(14.4)
Cálculo do ângulo crítico de extinção de corrente βc:
(14.5)
Para este circuito monofásico ponto médio tem-se m=2 e α= 23,58° logo,
βc=180+23,58=203,58°
(14.6)
Neste circuito contece um f to que deve ser lev do em consider ção, n obtenção do v lor de β, existe
um v ri ção no v lor de β que não pode ser c lcul d m tem tic mente. Est v ri ção decorre do f to de
que o ábaco de Puschlowski foi criado considerando que a tensão na carga se torna negativa, porém no circuito
de ponto médio no momento em que a tensão na carga ficaria negativa, o outro diodo entra em condução
forçando o bloqueio do diodo que estava em condução e coloca uma tensão positiva na carga porém ainda
menor que a fonte E. Esta mudança no valor de tensão causa uma variação na energia acumulada no indutor, o
que ocasiona uma variação no valor do ângulo de extinção de corrente, esta mudança pode fazer com que um
circuito onde se obtêm um v lor de β pelo ábaco próximo ao de βc, mas menor, o que resultaria em condução
descontínua, na realidade possua uma condução contínua muito próxima a critica, que é o caso que será
considerado neste circuito.
26
b)
Formas de onda:
400V
V(ωt)
0V
-400V
40V
VL
0V
-40V
50V
VD1
0V
-50V
5.0A
IL
0A
-5.0A
0.5A
I(wt)
0A
-0.5A
c)
3π
2π
π
0
4π
Cálculo da tensão média na carga VLmed:
(
∫√
)
(14.7)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o
ângulo de fim de condução do diodo.
∫
(
)
(14.8)
Cálculo da corrente média na carga ILmed:
(14.9)
d)
A potência não pode ser calculada por VLmed·ILmed devido a forma de onda de corrente ser
ondulada, o que significa que há a presença de harmônicas que não podem ser desconsideradas nos
cálculos.Assim a potencia na carga deveria ser calculada através de
(14.10)
27
15.
Considere o conversor abaixo com o diodo D1 queimado e também não queimado:
R=5Ω; L=3H; E=62V; Vo=220; f=60Hz; rt=10mΩ, Vto=0,6V; Ta=30°C; Rca=46°C/W.
V1(ωt)
D1
V2(ωt)
D2
R
V3(ωt)
D3
D4
L
E
a)
b)
c)
d)
C lcule o ângulo de extinção d corrente, modo de condução e βc.
Traçar as formas de onda V1, V2, V3, VL, IL , VD2 e I2.
A tensão e corrente média na carga.
Calcule a temperatura na cápsula do diodo D2.
Para circuito sem diodo queimado:
Neste caso o diodo D4 nunca entrará em condução, pois nunca terá tensão negativa na carga.
Cálculo do ângulo de extinção de corrente β:
Devido a presença da fonte é necessário verificar se o ângulo em que a fonte de entrada torna-se maior
do que o do valor da fonte E é maior ou menor do que 30° a fim de verificar a influência da fonte E no início de
condução do diodo.
311·sen(ωt)=62
Θ1 = ωt = 11,50°
(15.1)
Como o ângulo em que a fonte de entrada ultrapassa o valor da fonte E é menor do que 30°(ângulo em
que uma fonte de entrada se torna a fonte com o maior valor de tensão do circuito forçando a condução do
diodo) se tem
α=30°.
√
[
(15.2)
(15.3)
√
(
)]
[
(
)]
(15.4)
Através do ábaco de Puschlowski obtêm-se:
α=30° a= 0,2
cosΦ=0
β= 271°
(15.5)
Cálculo do ângulo crítico de extinção de corrente βc:
(15.6)
Para este circuito tem-se m=3 e α= 30° logo,
βc=120+30=150°
(15.7)
Como β>βc é condução contínua.
28
b)
Formas de onda
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
400V
VL
200V
0V
VD2
0V
-250V
-500V
IL
40A
ID2
20A
0A
c)
4π3π
2π
π
0
Cálculo da tensão média na carga VLmed:
(
∫√
)
(15.8)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o
ângulo de fim de condução do diodo.
(
∫
)
(15.9)
Cálculo da corrente média na carga ILmed:
(15.10)
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e β é m ior que βc o suficiente para considerarmos a corrente na carga
uma constante. Então :
(15.11)
Cálculo da corrente de pico no diodo VD:
√
√
√
√
(15.12)
29
Cálculo da corrente média no diodo:
No circuito trifásico o diodo conduz em 1/3 do tempo total do ciclo. Então:
(15.13)
Cálculo da corrente eficaz no diodo:
√
d)
∫(
(15.14)
)
√
√
Resistência junção ambiente
Cálculo da potência dissipada no diodo:
(15.15)
Cálculo da temperatura de cápsula:
(15.16)
Com diodo queimado
a)
Com o diodo queimado o circuito entrará em roda livre no momento em que a tensão na
carga tender a ficar negativa. Assim o circuito se comporta como um circuito RLE equação da corrente é dada
por
( )
(
)
(15.17)
Onde Im é corrente inst ntâne no momento em que ωt=π, que pode ser obtido p rtir d seguinte
expressão:
(
)
√
,*
( )
(
)
√
(
( )
√
(
{[
[
+
)
)
(
)+
( )-
(
(15.18)
(15.19)
)
)
(
)
(
(
√
( )
*
√
]
√
)]
(
)}
(15.20)
( )
Utilizando a equação 15.17 e fazendo il(t)=0 para achar o tempo em que a corrente zeraria no circuito RLE se
obtêm
(
)
(15.21)
s
Como um período da rede a 60 HZ é de 16,67ms verifica-se que o circuito tem condução contínua.
30
b)
Formas de onda
Deve ser lembrado que no momento em que a tensão na carga se torna negativa o diodo D4 entra em
condução criando roda-livre na carga
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
400V
VL
200V
0V
VD2
0V
-250V
-600V
IL
40A
ID2
20A
0A
c)
3π
2π
π
0
4π
Cálculo da tensão média na carga VLmed:
(
∫√
)
(15.22)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo.
(
∫
)
(15.23)
Cálculo da corrente média na carga ILmed:
(15.24)
Cálculo da corrente eficaz na carga ILef:
Sendo condução contínua, considera-se constante pois a constante de tempo é suficientemente maior
que o tempo em que as fontes de entrada estão com tensão menor que a fonte E na carga. Então:
(15.25)
Cálculo da corrente de pico dos diodos VDP:
√
√
√
√
(15.26)
31
Cálculo da corrente média no diodo:
Neste circuito cada diodo conduz em 1/2 do tempo total do ciclo. Então:
(15.27)
Cálculo da corrente eficaz no diodo:
√
d)
∫(
)
√
(15.28)
√
Resistência junção ambiente
Cálculo da potência dissipada nos diodos:
(15.29)
Cálculo da temperatura na cápsula:
(15.30)
16.
Considere o conversor b ixo onde V(ωt)=220sen(ωt)
E=60V; L=100mH; R=5Ω; f= 50Hz
D
1
R
L
V(ωt)
E
a)
Calcule o ângulo de extinção da corrente e defina o modo de condução.
b)
Apresente as formas de onda e calcule VLmed e ILmed..
c)
Sendo E=0V e R= 20Ω, dicione em nti-paralelo com a carga um diodo e calcule o valor da
indutância para se obter condução crítica.
Solução:
a)
Cálculo do ângulo de extinção d corrente β:
Com a presença de fonte E na carga, o ângulo de início de condução do diodo deix de ser α=0° e p ss
a ser o ângulo em que a fonte de entrada tem seu valor maior que o da fonte E, polarizando positivamente o
diodo, dando início a condução.
220·sen(ωt)=60
α= Θ1 = ωt = 15,83°=0,276 rad
(16.1)
(16.2)
√
[
(
)]
[
(
)]
(16.3)
32
Utilizando-se do ábaco de Puschlowski e aplicando médias sucessivas se obtêm os seguintes valores:
Para
Para
Para
a=0,2
a=0,4
a=0,3
cosΦ=0
β=274°
cosΦ=0,2
β=249°
cosΦ=0,1
β=261,5°
cosΦ=0,15
β=255,25°
cosΦ=0
β=236°
cosΦ=0,2
β=221°
cosΦ=0,1
β=228,5°
cosΦ=0,15
β=224,75°
cosΦ=0,15
β=240°=4,19 r d
(16.4)
Cálculo do ângulo crítico de extinção de corrente:
(16.5)
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
Para este circuito tem-se m=1 e α= 15,83°.
βc=360+15,83=375,83°
(16.6)
Como βc>β tem-se condução descontínua.
b)
Formas de onda:
V(ωt)
400V
0V
-400V
VL
400V
0V
-400V
VD1
0V
-200V
-400V
IL
8.0A
4.0A
0A
3π
2π
π
0
4π
Cálculo da tensão média na carga VLmed:
∫√
(
)
∫
(16.7)
33
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo (extinção d corrente β) e θ3 o ângulo de reinício de condução do diodo.
(
∫
)
∫
(16.8)
Cálculo da corrente média na carga ILmed:
(16.9)
c)
Indutância necessária para condução critica Lc:
Colocando um diodo em anti-paralelo, torna-se o circuito em um circuito monofásico de meia onda com
roda livre, onde para que haja condução critica é necessário que
(16.10)
Onde π é o ângulo em que se tem rod livre, ou sej , é o tempo em que o indutor se descarregará
tr vés do resistor té fonte de entr d volt r c rreg r o indutor. ω é freqüênci ngul r e τ é const nte
de tempo do circuito dada por L/R.
Portanto para que haja condução contínua é necessário que o tempo de 5τ sej m ior que o tempo em
que a fonte fica sem fornecer energia à carga. Logo.
(16.11)
17.
Para o retificador monofásico de onda completa com ponto médio abaixo.
R=2Ω; L=100mH; E=10V; V(ωt)=180sen(ωt); f=50Hz; rt=10mΩ; Vto=1V; Ta= 50°C; N1/N2=5
D
1
R
N
2
V(ωt)
L
N
1
N
2
E
D
2
a)
b)
c)
d)
C lcul r o ângulo de extinção d corrente, βc e definir o modo de condução.
Traçar as formas de onda VL, IL, v(ωt), i(ωt) e VD1.
Calcular VLmed e ILmed.
Calcule a temperatura na cápsula do componente sendo que Rthjc=1°C/W, Rthca=45°C/W.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
Para circuitos monofásicos tem-se:
Devido a presença de fonte E na carga o ângulo de início de condução do diodo deix de ser α=0° e
passa a ser o ângulo em que a fonte de entrada tem seu valor maior que o da fonte E, polarizando
positivamente o diodo dando início a condução.
36sen(ωt)=10
α =Θ1 = ωt = 16,13°=0,281 rad
√
(17.1)
(17.2)
34
[
(
)]
[
(
)]
(17.3)
Através do ábaco de Puschlowski e fazendo médias sucessivas obtêm-se:
α=16,13°
a=0,2
a=0,4
a=0,3
cosΦ=0
cosΦ=0
cosΦ=0
β=274°
β=236°
β=255°
(17.4)
Cálculo do ângulo crítico de extinção de corrente βc:
(17.5)
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
Para este circuito m=2 e α=16,13°.
logo,
βc=180+16,13°=196,13°
(17.6)
Como βc<β tem-se condução contínua.
b)
Formas de onda
V(ωt)
200V
0V
-200V
VL
40V
20V
0V
0V
VD1
-50V
-100V
10A
IL
0A
-10A
2A
I(wt)
0A
-2A
0
π
2π
3π
4π
35
c)
Cálculo da tensão média na carga VLmed:
(
∫√
)
(17.7)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o
ângulo de fim de condução do diodo.
(
∫
)
(17.8)
Cálculo da corrente média na carga ILmed:
(17.9)
Cálculo da corrente média no diodo:
Cada diodo conduz ½ do período total do ciclo:
(17.10)
Cálculo da corrente eficaz no diodo:
√
d)
∫(
)
√
(17.11)
√
Resistência junção ambiente
Cálculo da potência dissipada no diodo:
(17.12)
Cálculo da temperatura na cápsula do diodo:
(17.13)
18.
Para o retificador trifásico com ponto médio da figura abaixo.
V1(ωt)=√ 220sen(ωt); V2(ωt)=√ 220sen(ωt-120°); V3(ωt)=√
L=3000mH; E=100V; rt=10mΩ; Vto=1V; Ta=50°C.
V1(ωt)
D1
V2(ωt)
D2
220sen(ωt+120°); f= 60Hz; R=2Ω;
R
V3(ωt)
D3
L
E
a)
Traçar as formas de onda VL(ωt), IL(ωt), ID2 e VD2.
b)
Calcular VLmed, ILmed, ILef, IDmed, IDef. e VDP.
c)
Calcular o fator de potência da fonte
d)
Calcular o valor da resistência térmica entre junção e o ambiente para que o diodo D1 se
mantenha com uma temperatura inferior a 150°C.
36
Solução:
a)
Formas de onda:
Cálculo do ângulo de extinção de corrente β:
Devido a presença da fonte é necessário verificar se o ângulo em que a fonte de entrada torna-se maior
do que o do valor da fonte E é maior ou menor do que 30° a fim de verificar a influência da fonte E no início de
condução do diodo.
311·sen(ωt)=100
(18.1)
Θ1 = ωt = 18,76°
Como o ângulo em que a fonte de entrada ultrapassa o valor da fonte E é menor do que 30°(ângulo em
que uma tensão de linha se torna a maior no circuito forçando a condução dos diodos) se tem
α=30°.
(18.2)
(18.3)
√
[
(
)]
[
(
)]
(18.4)
Através do ábaco de Puschlowski e fazendo médias sucessivas obtêm-se:
α=30°
a= 0,2
cosΦ=0
β= 274°
a= 0,4
cosΦ=0
β= 236°
a= 0,3
cosΦ=0
β= 255°
(18.5)
Cálculo do ângulo crítico de extinção de corrente βc:
(18.6)
Para este circuito monofásico de meia onda tem-se m=1 e α= 30° logo,
βc=120+30=150°
(18.7)
Como β >βc tem-se condução contínua.
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
400V
VL
200V
0V
VD2
0V
-250V
-500V
IL
80A
ID2
40A
0A
0
π
2π
3π
4π
37
b)
Cálculo da tensão média na carga VLmed:
(
∫√
)
(18.8)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o
ângulo de fim de condução do diodo.
(
∫
)
(18.9)
Cálculo da corrente média na carga ILmed:
(18.10)
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e β é m ior que βc o suficiente para considerarmos a corrente na carga
uma constante. Então:
(18.11)
Cálculo da corrente de pico de D1 VD1:
√
√
√
√
(18.12)
Cálculo da corrente média no diodo:
No circuito trifásico, cada diodo conduz em 1/3 do tempo total do ciclo. Então:
(18.13)
Cálculo da corrente eficaz no diodo:
√
c)
∫(
)
(18.14)
√
√
Fator de potência:
(18.15)
Cálculo da potência ativa na carga:
(18.16)
Mas como cada fonte contribui com 1/3 da potência total se tem:
(18.17)
Cálculo da potência aparente da fonte de tensão:
(18.18)
Cálculo do fator de potência:
(18.18)
d)
Resistência junção ambiente:
Cálculo da potência dissipada por diodo:
(18.19)
Cálculo da resistência junção-ambiente
(18.20)
(18.21)
38
19.
Considere o conversor abaixo com:
R=10Ω; E=180V; Vo=220.
V1(ωt)
D1
V2(ωt)
D2
R
V3(ωt)
D3
E
a)
b)
c)
Traçar as formas de onda VL(ωt), IL(ωt), ID1 e VD1.
Calcular VLmed, ILmed, ILef, IDmed, IDef.
Calcular o fator de potência da fonte
Solução:
a)
Formas de ondas
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
400V
VL
200V
0V
VD1
0V
-250V
-500V
IL
20A
10A
0A
b)
π
0
3π
2π
4π
Calculo da tensão média na carga VLmed:
∫√
(
)
∫
(19.1)
Onde n é o número de pulsos do conversor,θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo (extinção d corrente β) e θ3 o ângulo de reinício de condução do diodo.
39
311·sen(ωt)=180
(19.2)
Θ1 = ωt = 35,36°=0,617 rad
Θ2=ωt=180-35,36=144,64°=2,524 rad
(19.3)
Θ3=150+5,36=155,36°=2,712 rad
(19.4)
(
∫
)
∫
(19.5)
Cálculo da corrente média na carga ILmed:
(19.6)
Cálculo da corrente eficaz na carga ILef:
√
√
∫(
(
)
√
)
(
∫ (
)
)
(19.7)
Cálculo da corrente média no diodo:
No circuito trifásico o diodo conduz em 1/3 do tempo total do ciclo. Então:
(19.8)
Cálculo da corrente eficaz no diodo:
√
c)
∫(
)
(19.9)
√
√
Fator de potência:
(19.10)
Cálculo da potência na carga:
(19.11)
Como cada fonte entrega 1/3 da potência total para a carga
(19.12)
Cálculo da potência aparente da fonte:
(19.13)
(19.14)
40
20.
Sabendo que a variação da tensão admitida no circuito é de 24V à 26V e que a potência
consumida pelo mesmo é 5W.
Vo= 220 V; f=60Hz
a)
Calcular e especificar o capacitor (C, Icef e Vmax)
b)
Calcular e especificar o transformador (tensão eficaz entrada, tensão eficaz de saída e
potência aparente).
Solução:
a)
Cálculo do capacitor
Como deseja-se uma tensão de pico de 26V e uma tensão mínima no capacitor de 24V tem-se:
(20.1)
Pelo ábaco da figura 10.9 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi se obtêm ωRC=32
A resistência pode ser obtida através da potência que é desejada pelo microprocessador. Assim
(20.2)
Portanto,
(20.3)
Calculo da corrente eficaz no capacitor:
Pelo ábaco da figura 10.10 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi obtêm-se
(20.4)
A tensão máxima do capacitor deve ser a tensão máxima desejada no circuito, ou seja
Vpk=26
(20.5)
b)
Cálculo do transformador
Cálculo da potência aparente do transformador:
Através do ábaco figura 10.29 do livro de Eletrônica de Potência 6ª edição de Ivo Barbi se obtêm
FP=0,45, portanto
(20.6)
Cálculo da tensão de saída do transformador:
√
Cálculo da tensão de entrada do transformador
(20.7)
(20.8)
41
21.
Considere
estrutur
b ixo onde f=60Hz, rt=11mΩ, Vto=0,85V, Rthjc=2°C/W e Rthcd = 1°C/W,
Ta= 50°C. V1(ωt)=√ 110sen(ωt); V2(ωt)=√ 110sen(ωt-120°); V3(ωt)=√ 110sen(ωt+120°); L=130mH e R=10Ω.
D
1
V1(ωt
)
D
2
D
3
R
V2(ωt
)
L
V3(ωt
)
D
4
D
5
D
6
a)
Calcule o valor da tensão média na carga e da corrente média na carga.
b)
Determine o valor da resistência térmica do dissipador para um dos diodos para que a
temperatura de junção se mantenha em 140°.
c)
Caso o diodo D6 esteja com problemas (circuito aberto), esboce a forma de onda de tensão
na carga e calcule o valor médio da tensão na carga.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
Para circuitos em ponte de Graetz tem-se:
α=60°.
(21.1)
(21.2)
√ √
[
(
)]
[
(
)]
(21.3)
Através do ábaco de Puschlowski e fazendo médias sucessivas obtêm-se:
α=60° a= 0
cosΦ=0,2
β= 300°
(21.4)
Cálculo do ângulo crítico de extinção de corrente βc:
(21.5)
Para este circuito tem-se m=6 e α= 60° logo,
βc=60+60=120°
(21.6)
Como βc<β tem-se condução contínua.
42
Formas de onda
V1(ωt)
200V
V2(ωt)
V3(ωt)
0V
-200V
300V
VL
200V
100V
0V
VD1
0V
-200V
-400V
IL
30A
20A
10A
0A
π
0
3π
2π
4π
Cálculo da tensão média na carga VLmed:
(
∫√
)
(21.7)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução de um par de diodos, θ2
é o ângulo de fim de condução do par de diodos.
∫ √
(
√
)
(21.8)
Cálculo da corrente média na carga ILmed:
(21.9)
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e β é m ior que βc o suficiente para considerarmos a corrente na carga
uma constante. Então :
(21.10)
Cálculo da tensão de pico de D1 VD1:
√
√
√
√
(21.11)
Cálculo da corrente média no diodo:
No circuito trifásico o diodo conduz em 1/3 do tempo total do ciclo. Então:
(21.12)
43
Cálculo da corrente eficaz no diodo:
√
b)
∫(
(21.13)
)
√
√
Cálculo da potência dissipada em um diodo
(21.14)
Cálculo da resistência junção ambiente:
(21.15)
(21.16)
c)
Verificação da condução
Verificando as formas de onda base, verifica-se que na falta de um diodo a tensão na carga não ficará
negativa, o que resultará no mínimo em condução critica, mas devido a presença do indutor pode se dizer que
terá condução contínua.
V1(ωt)
200V
V2(ωt)
V3(ωt)
0V
-200V
400V
VL
200V
0V
0V
VD1
-200V
-400V
40A
IL
20A
0A
3π
2π
π
0
4π
Cálculo da tensão média na carga VLmed:
(
∫√
∫
(
)
∫
)
(21.17)
(
)
(21.18)
44
Cálculo da corrente média na carga ILmed:
(21.19)
22.
Seja o circuito :
D1
R
V1(ωt)
L
R= 100Ω; L=500mH; Vo=220V; f=60Hz.
Calcular
a)
Tensão média na carga
b)
Corrente média na carga
c)
O v lor d corrente inst ntâne de c rg qu ndo ωt=π, no 1° semi-periodo.
d)
Verificar se a condução é contínua ou descontínua.
Solução:
a)
Cálculo da tensão média na carga VLmed:
(
∫√
)
(22.1)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo D1, θ2 é o
ângulo de fim de condução do diodo D1 e entrada em condução do diodo de roda livre.
(
∫
b)
)
(22.2)
Cálculo da corrente média na carga ILmed:
(22.3)
c)
Valor da corrente inst ntâne de c rg qu ndo ωt=π no primeiro semi-periodo:
sabe-se que a formula da corrente no tempo para circuitos rl é dada por
( )
√
(
)
(
)
(22.4)
Onde,
√
(
(
)
)
(22.5)
(
)
(22.6)
(22.7)
Assim
( )
√
(
)
(
)
(22.8)
45
d)
Verificação condução contínua
Como o circuito permanece em rod livre por π r d, tem-se ωc=π. Logo,
(22.9)
Assim verifica-se que é condução contínua e pelos valores obtidos pode-se dizer que é contínua
ondulada.
400V
V (ωt)
0V
-400V
400V
VL
200V
-10V
0V
VD1
-200V
-400V
2.0A
IL
1.0A
0A
3π
2π
π
0
4π
23.
Seja o retificador mostrado abaixo, onde V1=100V (pico); R= 10Ω e L=0,01H; f=60Hz. C lcul r
VLmed, ILmed., potência absorvida pela carga e o FP da estrutura.
D1
R
V1(ωt)
L
46
Solução:
Cálculo do ângulo de extinção de corrente β:
Para circuitos monofásicos tem-se:
Ângulo de início de condução α= 0
(23.1)
√
(
)
[
(
)]
(23.2)
Através do ábaco de Puschlowski obtêm-se com:
α=0
a= 0
cosΦ=0,9
β=206°
cosΦ=1,0
β=180°
(23.3)
Fazendo uma média obtêm-se
α=0
a= 0
cosΦ=0,95
β=193°
Cálculo do ângulo crítico de extinção de corrente βc:
(23.4)
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
Para circuito monofásico de meia onda tem-se α=0 e m=1.
Βc=360°
(23.5)
Como βc>β tem-se condução descontínua.
Formas de onda:
100V
V(ωt)
0V
-100V
100V
VL
0V
-100V
0V
VD1
-50V
-100V
10.0A
IL
5.0A
0A
0
π
2π
3π
4π
47
Cálculo da tensão média na carga VLmed:
(
∫√
)
(23.6)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução e θ2 é o ângulo de fim
de condução do diodo.
(
∫
)
(23.7)
Cálculo da corrente média na carga ILmed:
(23.8)
Cálculo do fator de potência:
Para o cálculo do fator de potência é necessário o valor da corrente eficaz na carga é na fonte de tensão,
que neste caso é o mesmo para os dois.
Sendo
(
)
(
)
(23.9)
Utilizando o ábaco da Fig.2.8 do livro de Eletrônica de Potência 6ª edição de Ivo Barbi para correntes
normalizadas obtêm-se:
Ief=0,5A
(23.10)
(
(23.11)
Portanto:
√
)
√
(23.12)
Potência dissipada na carga:
P=R·ILef2
(23.13)
P=10·4,68²=218,9 W
Potência dissipada na fonte:
S=Vef·Ief
(23.14)
S=70,71·4,68=330,93 VA
(23.15)
24.
Considere o retificador trifásico com ponto médio da figura abaixo. Sabe-se que o diodo D1
está queimado (aberto) e que:
V1(ωt)=√ 220sen(ωt); V2(ωt)=√ 220sen(ωt+120°); V3(ωt)=√
L=800mH; D1=D2=D3=SKN 20/04, rt= 11mΩ, Vto=1V; Ta=30°C.
V1(ωt)
D1
V2(ωt)
D2
220sen(ωt-120°); f= 60Hz; R=10Ω;
R
V3(ωt)
D3
L
48
a)
Traçar as formas de onda V1, V2, V3, VL, IL e VD2.
b)
Calcular VLmed, ILmed, ILef, VD1, IDmed, IDef.
c)
Calcular o valor da resistência térmica entre junção e o ambiente para que o diodo D2 se
mantenha com uma temperatura de junção inferior à 150°C.
Solução:
a)
Formas de onda
Verificação condução contínua
Devido a presença do diodo queimado verifica-se se o β possui um v lor de ângulo m ior que o ângulo
em que o próximo diodo entre em condução, assim tendo condução continua. Em um sistema trifásico na
queima de um diodo a carga permanece com tensão negativa durante 60°. Logo é necessário que
β=180°+60°=240° p r que o proximo diodo entre em condução. ssim
3 °
(24.1)
(24.2)
√
[
(
)]
[
(
)]
(24.3)
cosΦ=0 β= 330°
(24.4)
Através do ábaco de Puschlowski obtêm-se:
α=30° a= 0
Assim como β é m ior que 240°, é condução contínua
É condução contínua
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
VL
400V
VL
0V
-400V
0V
VD2
-250V
-500V
20A
IL
10A
0A
0
b)
π
2π
3π
4π
Cálculo da tensão média na carga VLmed:
49
(
∫√
)
(24.5)
Onde n é o número de pulsos do conversor,θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo.
(
∫
)
(24.6)
Cálculo da corrente média na carga ILmed:
(24.7)
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e a constante de tempo é grande o suficiente para considerarmos a
corrente na carga uma constante. Então :
(24.8)
Cálculo da tensão de pico de D2 VD2:
√
√
√
√
(24.9)
Cálculo da corrente média no diodo:
Neste circuito o diodo conduz em 1/2 do tempo total do ciclo. Então:
(24.10)
Cálculo da corrente eficaz no diodo:
√
c)
∫(
)
√
√
(24.11)
Cálculo da potência dissipada no diodo:
(24.12)
Cálculo da resistência junção-ambiente
(24.13)
50