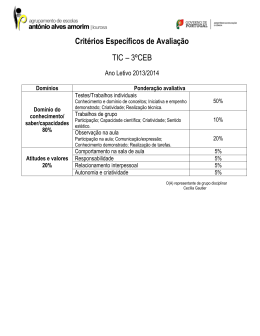
1 AVALIANDO O CLIMA PARA CRIATIVIDADE NAS AULAS DE MATEMÁTICA
Alexandre Tolentino de Carvalho. Universidade de Brasília.
[email protected]
RESUMO: Nas relações estabelecidas na escola, gera-se um clima psicológico nesse
ambiente que tanto pode propiciar o desenvolvimento do potencial criativo dos indivíduos,
como pode atrapalhá-lo. Porém, na literatura consultada, faltam estudos empíricos que tratem
dos fatores constituintes do clima de sala de aula para a criatividade em Matemática e são
insuficientes os instrumentos validados estatisticamente para mensurar esse clima. O presente
artigo descreve um estudo empírico-analítico realizado com 324 alunos de escolas públicas e
privadas na faixa etária de 9 a 14 anos dedicado a compreender os fatores presentes na
formação do clima de sala de aula para a criatividade nas aulas de Matemática. Apresenta-se a
Escala de Clima para Criatividade nas Aulas de Matemática, instrumento resultante desse
estudo e que serve como ferramenta para professores, gestores, pesquisadores e alunos
poderem avaliar potencialidades e fragilidades envolvidas na constituição do clima favorável
à criatividade nas aulas de matemática.
Palavras-chave: criatividade em matemática, educação matemática, clima de sala de aula
para criatividade
Justificativa
Parece consenso entre os pesquisadores em educação matemática que as habilidades
matemáticas não são trabalhadas em sua completude sendo que, aparentemente, as habilidades
escolares lógicas, ligadas ao pensamento convergente, recebem prioridade nos planos de aula
em detrimento de habilidades que demandam mais tempo e uma atenção maior por parte do
professor no sentido tanto de pesquisar, planejar, elaborar e acompanhar o desenvolvimento
dessas aulas. Como consequência, as atitudes dos alunos com o conhecimento matemático
tornam-se mais automatizadas e menos reflexivas.
A título de exemplo, podemos citar os estudos de Haylock (1997) que percebeu a
existência de uma tendência entre os alunos de fixação de conteúdos universais (ou seja, seus
pensamentos sobre um problema ficam restritos a uma variedade de elementos insuficientes
ou inadequados) e fixação algorítmica (na qual eles aderem a um procedimento de rotina ou
resposta estereotipada, mesmo quando esta se torna ineficiente ou inapropriada para o
problema em questão). Haylock propõe, então que a superação dessa rigidez de pensamento
pode ser um aspecto relevante para a resolução de problemas matemáticos.
2 Ainda nesse sentido, Valdés (2010) identifica que muitos professores, guiados por
uma concepção puramente formal da natureza da matemática, consideram que essa disciplina
escolar deve desenvolver formas de raciocínio associadas ao pensamento lógico, ou seja,
prioriza-se o pensamento convergente em que as ações são “associadas ao pensamento
formal” (VALDÉS, 2010, p. 8) compreendendo os raciocínios indutivo, dedutivo e por
analogia. No entanto, ter um pensamento lógico bem desenvolvido é insuficiente para a
resolução de problemas matemáticos que requerem uma “elevada dose de imaginação,
fantasia e criatividade” (p. 6).
Esses autores estão se referindo ao desenvolvimento das habilidades criativas nas
aulas de matemática, uma das facetas da matemática escolar que tem sido negligenciada
quando o professor prioriza o uso indiscriminado de fórmulas, algoritmos e pensamento
rígido no qual se ensina, se aprende e se reproduz formas únicas de solução de problemas
matemáticos. Problemas esses que, segundo Piggott (2007) se restringem a abordar um
contexto que é muito familiar ao aluno, quase sempre retratando um conceito matemático que
acabaram de aprender e que nada trazem de desafiador, pois, são dadas pistas claras sobre o
conhecimento a ser aplicado em sua resolução.
Nesse sentido, o presente trabalho se mostra importante na medida em que apresenta
o desenvolvimento da criatividade em matemática como alternativa viável para as formas
tradicionais de ensino dessa área do conhecimento. Partimos do pressuposto de que o
desenvolvimento da criatividade em matemática precisa ocorrer em um ambiente em que se
constitua um clima de sala de aula propício para tanto.
Objetivos
É objetivo desse trabalho investigar os fatores que influenciam o processo de
construção do clima favorável para a criatividade em matemática e apresentar a Escala de
Clima para Criatividade nas Aulas de Matemática como um instrumento de avaliação e
identificação de potencialidades e fragilidades existentes no ambiente escolar que interferem
no desenvolvimento do potencial criativo dos alunos.
Literatura Consultada
Não há dúvidas entre os pesquisadores que o desenvolvimento do potencial criativo
dos alunos precisa fazer parte da pauta das habilidades matemáticas a serem desenvolvidas no
espaço escolar (KRUTETSKII, 1976; GONTIJO, 2007; KATTOU et al, 2013). Um dos
ambientes mais investigados na pesquisa relacionada à criatividade é a escola (FLEITH,
3 2010). Sendo um ambiente formado por pessoas que relacionam-se entre si e que relacionamse com os conhecimentos matemáticos, acaba sendo desenvolvido um clima nesse ambiente
que tanto pode propiciar o desenvolvimento do potencial criativo dos indivíduos, como pode
servir de barreira que impede a criatividade de aflorar.
Fernandes (2008) lembra que na sala de aula “confluem personalidades, motivações
e capacidades muito díspares, não sendo, pois fácil criar e alimentar relações de afeto, de
carinho e amizade, caso não exista um bom clima de aceitação das diferenças e de respeito
mútuo” (p. 16). Portanto, para estudar o modo como se organiza o clima de sala de aula e,
especificamente, estudar o clima para criatividade nas aulas de Matemática, é necessário se
concentrar tanto no ambiente como nas pessoas que se relacionam nesse ambiente.
Na literatura consultada, não se encontram estudos empíricos que tratem
especificamente dos fatores ambientais que influenciam no desenvolvimento das habilidades
criativas em Matemática. Levando-se em conta a importância de se empreender pesquisas
relacionadas ao clima para criatividade nas aulas de Matemática e a insuficiência de estudos e
instrumentos de mensuração desse clima específicos nessa área de ensino, o presente artigo se
dedica a descrever um estudo realizado nos anos de 2013 e 2014 com alunos compreendidos
na faixa etária de 9 à 14 anos em busca de analisar os fatores e dimensões presentes na
formação do clima de sala de aula para a criatividade nas aulas de Matemática e de apresentar,
como alternativa para mensuração desses fatores, a Escala de Clima para Criatividade nas
Aulas de Matemática, instrumento resultante destes estudos.
Para constituir um entendimento sobre o clima para criatividade nas aulas de
Matemática, foram consultadas 5 grandes áreas envolvendo a literatura sobre clima de sala de
aula (BRUNET, 1992; FERNANDES, 2008; RODRIGUES GARRÁN, 2004; SCHMIDT &
ĈAGRAN, 2006), sobre Clima para criatividade em sala de aula (ALENCAR, 2007;
AMABILE et al., 1996; FLEITH e ALENCAR, 2005) e sobre clima nas aulas de Matemática
(HALADYNA, SHAUGHNESSY E SHAUGHNESSY, 1983; MESSIAS & MONTEIRO,
2009). A consulta à literatura abarcou, ainda, estudos sobre criatividade (ALENCAR &
FLEITH, 2003; AMABILE, 1983; CSIKSZENTMIHALYI, 1996; LUBART, 2007;
SIMONTON, 1988; STERNBERT,1991) e sobre criatividade em Matemática (GONTIJO,
2007;
HADAMARD,2009/1963;
HASHIMOTO,
1997;
HAYLOCK,
1987,
1997;
KRUTETSKII, 1976; NADJAFIKHAHA, YAFTIAN & BAKHSHALIZADEH, 2012;
SIRIRAMAN, 2004; VALDÉS, 2010). Por motivo de síntese, não iremos abordar as
contribuições de todos esses estudiosos. No entanto, buscaremos apontar alguns pontos
4 básicos indispensáveis para a compreensão de como concebemos os entendimentos sobre o
clima para criatividade nas aulas de Matemática.
a) Clima de sala de aula. Brunet defende que o “clima organizacional representa as
percepções dos atores escolares em relação às práticas existentes numa dada organização”
(citado em SANTOS, 2010, p. 42). O autor aponta três variáveis como determinantes da
constituição do clima de sala de aula: (I) a estrutura: características físicas da organização
descritas, por exemplo, nos programas escolares; (II) o processo organizacional: a forma
como se dá a gerência dos recursos humanos como, por exemplo, a forma em que se resolvem
os conflitos, a política de recompensas e o modo em que se organiza o projeto educativo; (III)
as variáveis comportamentais: modos de organizações individuais e grupais.
Em um estudo realizado com alunos do 7º, 8º e 9º anos do 3º ciclo de uma escola
básica de Portugal, Fernandes (2008) chegou a um modelo teórico sobre o clima de sala de
aula no qual três dimensões são responsáveis pela constituição da representação dos alunos
sobre o clima de sala de aula nas disciplinas de Matemática e de educação visual e tecnologia:
(a) a organização e participação dos alunos nas aulas (b) o relacionamento interpessoal
professor/alunos e alunos/alunos e (c) a gestão preventiva ( por exemplo, intervenção do
professor face aos conflitos e comportamentos de indisciplina).
b) Clima de sala de aula para criatividade. Um atual trabalho relacionado aos estudos sobre
o clima para criatividade em sala de aula pode ser atribuído à Fleith (2010). A autora
apresenta a escala sobre o Clima para Criatividade em Sala de Aula (FLEITH; ALENCAR,
2005) construída para avaliar o clima para criatividade em sala de aula e validada por meio de
análise fatorial, onde foi utiliza uma amostra de alunos de 3ª e 4ª séries do ensino fundamental
(atualmente 4º e 5º anos do ensino fundamental). Os itens estão distribuídos em cinco fatores:
(a) suporte da professora à expressão de ideias do aluno; (b) autopercepção do aluno com
relação à criatividade; (c) interesse do aluno pela aprendizagem; (d) autonomia do aluno; (e)
estímulos da professora à produção de ideias do aluno.
O instrumento validado por Fleith e Alencar forneceu muitos elementos para a
elaboração da escala apresentada neste estudo. Alguns itens foram adaptados da escala das
autoras e utilizados na validação do instrumento resultante no presente trabalho.
c) Clima nas aulas de Matemática. Ao pesquisar a motivação para a matemática, o clima de
sala de aula de matemática e a relação entre essas duas variáveis, Messias e Monteiro (2009)
recorrem a dois instrumentos: à escala de motivação “Eu e a matemática” a escala de “Clima
de Sala de aula de Matemática” e apresentam conclusões interessantes.
5 Um aspecto importante do estudo de Messias e Monteiro (2009) para o entendimento
que estamos querendo construir sobre o clima para criatividade nas aulas de matemática
refere-se a caracterização da percepção do clima de sala de aula de matemática dos alunos 5º,
6º e 7º anos de escolaridade. Para tanto, as autoras utilizaram a escala de clima social de sala
de aula (MATA, MONTEIRO, & PEIXOTO, 2008). Após realizarem a análise fatorial, a
escala ficou composta por 32 itens distribuídos em 6 dimensões: (a) suporte social dos colegas
(avalia a percepção que o aluno tem em ralação ao apoio, ajuda e preocupação dada pelos
colegas); (b)suporte social do professor (percepção que os alunos têm do suporte dado pelo
professor nas aulas de Matemática); (c) atitude em relação à Matemática (avaliação da atitude
dos alunos em relação à matemática, ou seja, se participa nas atividades propostas e se gosta
delas ou se as evita; (d) aprendizagem cooperativa (percepção que os alunos têm a respeito de
gostarem e participarem das atividades de cooperação que envolvem ajuda e partilha); (e)
aprendizagem individualista (avaliação da percepção que os alunos têm sobre gostarem de
trabalhar individualmente ou se esse trabalho individual ocorre nas aulas de matemática); (f)
aprendizagem competitiva (percepção que os alunos têm acerca de apreciarem o método de
aprendizagem competitivo ou se esse método ocorre em sala de aula.
O trabalho de Haladyna, Shaughnessy e Shaughnessy (1983) também envolveu
estudos sobre clima de sala de aula de Matemática. Os autores desenvolveram um modelo
hipotético no qual os fatores qualidade do professor, clima sócio-psicológico de sala de aula e
clima da gestão/organização da sala de aula foram utilizados para mensurar a atitude em
relação à Matemática de alunos da 4ª, 7ª e 9ª séries. Os autores definem atitude para com a
Matemática como uma disposição emocional geral para a matéria escolar de Matemática,
valorizada por ser um resultado importante para a escola em si mesma, por ser frequentemente
de cunho positivo e ligeiramente relacionada com o sucesso e por poder aumentar a tendência
para eleger Matemática como possibilidade de carreira nesse campo. Desse modo, os autores
se concentraram na análise dos fatores endógenos à sala de aula, postulando que “o
desenvolvimento de atitudes em relação à Matemática é suscetível de ser influenciado pelo
professor e pelo ambiente de aprendizagem (por vezes referido como variáveis climáticas em
sala de aula) ” (p. 20).
d) Estudos sobre criatividade. Os pesquisadores que se dedicam a estudar a criatividade sob
a abordagem sistêmica revelam a importância do ambiente para o desenvolvimento da
criatividade e constituíram a quarta área de pesquisa utilizada para a compreensão do clima
para criatividade nas aulas de matemática. Amabile (1983) revela a importância das
influências do ambiente social para o desenvolvimento da motivação, de atitudes e
6 habilidades. Csikszentmihalyi (1996) elenca o meio social e cultural como espaço em que a
criatividade ocorre podendo inibir ou estimular a atividade criativa do indivíduo. Sternberg e
Lubart (1991) se remetem ao contexto ambiental como um importante fator para o
desenvolvimento da criatividade favorecendo a geração de novas ideias, encorajando e dando
suporte à geração de produtos criativos e avaliando o produto criativo. Simonton (1988)
avalia a criatividade como um fenômeno social devendo ser estudada por meio da
investigação das influências de variáveis sociais, políticas e culturais não podendo ser
compreendida fora do contexto social na qual ocorre.
e) Estudos sobre criatividade em Matemática. A quinta e última área do conhecimento
consultada refere-se à criatividade em matemática da qual já tratamos no início dessa
introdução. Além desses pontos abordados, podemos citar, por exemplo, Hashimoto (1997)
que evidencia a importância de se fomentar a criatividade em Matemática nos espaços
escolares por meio de atividades que oportunizem aos alunos formas diversas de pensar sobre
um problema a ser resolvido.
Nadjafikhaha, Yaftian e Bakhshalizadeh (2012) afirmam que pesquisas sobre a natureza da
criatividade indicam que estimular a criatividade depende fortemente dos ambientes de
aprendizagem, sendo professores um dos componentes eficazes deste ambiente quando se
pretende fomentar a criatividade matemática. No entanto, os autores advertem que deve-se
explorar em que medida os professores estão cientes da concepção e implementação de
ambientes de aprendizagem que apoiam a promoção da criatividade matemática. Nesse
sentido, Nadjafikhaha, Yaftian e Bakhshalizadeh (2012) alertam que “assim, é necessário dar
mais profunda atenção à capacitação de professores especialmente melhorando sua
capacidade para projetar e implementar ambientes educacionais que promovam a criatividade
em matemática” (p. 289). Para tanto, os autores sugerem que os professores devem se adaptar
as abordagens de ensino que reconhecem o potencial dos alunos para a geração de múltiplas
soluções para um determinado problema, em vez de enfatizar apenas o trabalho com
algoritmos, regras e procedimentos para encontrar uma única resposta correta para o
problema. Assim, o professor precisa tentar proporcionar um ambiente seguro no qual os
alunos possam ir além da verdade conhecida e oferecer oportunidades para o fluxo de
pensamentos, proporcionando também ambientes de sala de aula em que os alunos
compartilham suas percepções e ideias.
Um fator presente na literatura sobre criatividade em Matemática refere-se ao
trabalho em grupo, momento em que as interações entre os sujeitos podem favorecer o
desenvolvimento do potencial criativo dos indivíduos. Valdés (2010) aponta como uma das
7 premissas para a reestruturação do processo de ensino-aprendizagem de Matemática de
maneira que se estimule e se desenvolva as potencialidades criativas do aluno: “estimular o
trabalho cooperativo nas salas de matemática, o exercício da crítica, a participação e a
colaboração, a discursão e a defesa das próprias ideais e assumir a tomada conjunta de
decisões1” (p.11).
Em um estudo envolvendo cinco matemáticos criativos buscando compreender como
esses sujeitos criavam matemática, Sriraman (2004) concluiu que a interação social,
juntamente com a imaginação, a heurística, a intuição e a prova foram as características
comuns de criatividade matemática evidenciadas pelos sujeitos da pesquisa.
O clima para criatividade em Matemática
Como dito anteriormente, não foram encontradas correspondências que diziam
respeito aos estudos relacionados com o clima para criatividade nas aulas de matemática.
Nessa lógica, buscam-se aportes teóricos nos contributos anteriormente abordados para poder
avançar nas definições sobre clima para criatividade nas aulas de Matemática.
Primeiramente, pode-se assumir o clima para criatividade nas aulas de Matemática
mergulhado em uma estrutura afetivo-emocional, partindo da concepção de que a escola é um
espaço de encontro da criança com o conhecimento. No caso da Matemática, inspirando-se
em Krutetskii (1976), as aulas são os momentos de encontro da criança com a Matemática
escolar e com a criatividade em Matemática, encontro que se dá em profunda interação entre
aluno-aluno, aluno-professor e aluno-conhecimentos.
Partindo dos contributos acima abordados, assume-se que no clima para criatividade
em Matemática, o envolvimento físico e a estrutura apontam os recursos que contribuem para
a constituição do ambiente propício à criatividade como a forma em que o professor organiza
o espaço, o tempo e os materiais escolares e os objetos de conhecimento a serem
desenvolvidos no planejamento das aulas.
Dessa maneira, quando no presente estudo se apresentar o termo Clima para
criatividade nas aulas de Matemática, estaremos nos referindo à confluência de diversos
fatores que determinam as percepções dos alunos à cerca do valor que se atribui à atividade
criativa nas aulas de Matemática e que, consequentemente, interferem na própria atividade
1
Tradução e grifo nosso. 8 criativa do sujeito matematizador, tendo em vista que essas percepções convertem-se em
bases para a ação do indivíduo.
Esses contributos fundamentaram e deram origem a uma escala que busca avaliar a
percepção de alunos do 5º ano do Ensino Fundamental quanto ao clima para criatividade nas
aulas de Matemática, focando-se, por tanto, nos fatores ambientais que influenciam o
desenvolvimento do potencial criativo dos sujeitos respondentes ao instrumento. Lubart
enfatiza que “o ambiente avalia a criatividade através de julgamento social” (2007, p.18).
Pasquali (2010) lembra que “avaliar parece ser uma fatalidade do ser humano com relação ao
seu meio ambiente, incluindo ali, o meio físico bem como o social” (p.11). Sendo assim, em
meio à constante necessidade humana de avaliar os fatos ocorridos ao seu redor e
considerando-se a importância dos julgamentos sociais na constituição das percepções
individuais, essa escala se fundamenta como uma ferramenta útil na avaliação do clima para
criatividade nas aulas de Matemática.
Metodologia
As investigações foram orientadas por um estudo empírico-analítico antecedido pela
consulta à literatura acima descrita. Nesse sentido, foram elaborados inicialmente 53 itens
buscando refletir os aspectos acima citados, estruturados em uma escala Likert de 4 pontos
variando do valor 1, correspondente à opção nunca, ao valor 4, relacionado à opção sempre. A
linguagem dos itens foi construída por meio de frases afirmativas para garantir a compreensão
dos respondentes buscando, ainda, manter uma redação padronizada de modo a facilitar a
leitura das frases e enfatizar o fato de que os participantes devem avaliar o que ocorre
somente nas aulas de Matemática. Ainda, no intuito de auxiliar o entendimento dos
participantes adequando o instrumento à faixa etária dos respondentes, buscou-se, por meio de
recursos pictóricos, representar os valores atribuídos na escala, por meio da gradação que se
estende de uma figura de uma casca de sorvete referente ao valor “NUNCA”, passando por
uma figura de uma bola de sorvete referente ao valor “POUCAS VEZES”, outra figura de
duas bolas de sorvete referente ao valor “MUITAS VEZES” e chegando a figura de três bolas
de sorvete referente ao valor “SEMPRE”, como se pode observar abaixo:
9 Figura 1 – Recurso Pictórico da Escala de Clima para Criatividade nas Aulas de
Matemática
A validação desse instrumento se deu em três momentos distintos necessários para
que a escala pudesse realmente mensurar aquilo que se propõe de forma eficaz, adequada e
confiável. Apresentamos, a seguir, um breve detalhamento desse processo:
a)
A análise inicial foi realizada pelo julgamento de uma banca de três
especialistas que deveriam julgar os itens quanto ao seu propósito de mensuração da
percepção dos alunos em relação ao clima para criatividade nas aulas de Matemática. Após
esse julgamento, foram sugeridas alterações de termos e sugestões de novos itens ficando a
versão para análise semântica composta por 55 itens no total.
b)
Em seguida procedeu-se à análise semântica em que cinco colaboradores,
alunos do 5º ano do Ensino Fundamental de uma escola pública, avaliaram a adequação
vocabular dos itens à faixa etária correspondente. Segundo Pasquali (1999), os itens devem
ser formulados com uma linguagem apropriada (critério de clareza) de modo que sejam
compreendidos por todos os membros da população (critério de credibilidade). Nessa etapa de
análise, os alunos demonstraram compreensão vocabular e nenhuma alteração foi realizada.
c)
E, finalmente, após a validação semântica, o instrumento foi aplicado a uma
amostra de 324 estudantes seguindo a recomendação de Gorsuch (1983) que indica a
aplicação em uma amostra que represente uma proporção de 5 alunos para cada item
constante na escala ou por um total de pelo menos 200 sujeitos. Desses alunos, 200 estavam
matriculados em escolas públicas e 124 em escolas particulares. A confiabilidade do
instrumento se constituiu mediante análise fatorial, momento no qual verificou-se sua
estrutura interna e foi realizada a extração de fatores. Por meio do pacote estatístico SPSS
versão 20.0, realizou-se uma análise exploratória dos dados coletados na aplicação da versão
preliminar da escala, procedendo-se, posteriormente, à análise estatística desses dados. Com a
análise exploratória dos componentes principais, buscou-se descrever e explorar as
características principais dos resultados encontrados e investigou-se a presença, nos dados
levantados, de pressupostos estatísticos que demonstrassem a possibilidade de fatorabilidade
do instrumento. Em seguida, analisou-se os fatores constituintes da escala e a consistência
interna, momento no qual se verificou a fidedignidade de cada um desses fatores por meio do
Alfa de Cronbach. O alfa de Cronbach mede a consistência interna de um instrumento ou
partes de um instrumento por meio de uma escala que varia de 0 à 1, sendo que, enquanto
mais próximo do 1, mais fidedigno, ou seja, confiável é o fator para medir aquilo que
pretende medir. Pasquali (1997) lembra que a “fidedignidade ou precisão de um teste diz
10 respeito à característica que ele deve possuir, a de medir sem erros” (p.127). Maroco e GarciaMarques (2006), citando Nunnally (1978) lembram que, de um modo geral, um instrumento
ou teste é classificado como tendo confiabilidade apropriada quando o α é pelo menos 0,70.
No entanto, em alguns casos é aceitável um α de pelo menos 0,60, desde que “os resultados
obtidos com esse instrumento sejam interpretados com precaução e tenham em conta o contexto
de computação do índice” (DeVellis, 1991 citado em Maroco e Garcia-Marques, 2006, p. 73).
Desse modo, um dos critérios para a manutenção de itens e para a definição da quantidade de
fatores constituintes da escala apresentada no presente trabalho diz respeito ao valor do alfa
de Cronbach definidor da consistência interna desses fatores.
Resultados e Conclusões
Ao ser realizada a extração dos componentes principais observou-se a fatorabilidade
da matriz, ou seja, a possibilidade de existência de fatores. Foram apontados índices
favoráveis indicativos da fatorabilidade da matriz, dentre os quais, destacamos o índice de
adequação da amostra KMO DE 0,801 indicando matriz fatorável e ótima adequação do
tamanho da amostra tendo em vista que a literatura evidencia que valores acima de 0,80 são
considerados ótimos.
Lançando-se mão da Análise dos Componentes Principais, estimou-se o número
inicial de 19 fatores tendo como referência o critério de Kaiser onde o eingenvalue de cada
fator deve ser igual ou superior a 1. Levando em conta o número grande de fatores extraídos
por meio desse critério, passou-se a analisar a variância explicada pelo fator devendo ser de
no mínimo 3%, o que sugeriu a extração de 6 fatores. A inspeção do gráfico Scree Plot
também sugeriu a existência de 6 fatores. No entanto, o sexto fator foi eliminado por possuir
índice de confiabilidade baixo (alfa de Cronbach) e conter apenas 3 itens que não
apresentaram carga fatorial superior à 0,30 nos outros fatores. Três itens pertencentes aos
outros cinco fatores foram eliminados por não apresentarem um sentido teórico que
justificasse a presença daquele item no fator ao qual foi alocado. Dessa maneira, após as
análises realizadas, a matriz deu origem à escala composta por 45 itens dispostos em cinco
fatores que explicam 33,07% de variância total. A escala denominada Escala de Clima para
Criatividade em Matemática ficou assim constituída:
Compondo o Fator 1, temos 11 itens que dizem respeito à relação do aluno com a
Matemática desenvolvida em sala de aula, onde ele pode expressar a percepção sobre essa
área do conhecimento, demonstrando o nível de prazer e de desempenho nessa disciplina,
assim como avaliar o seu nível de criatividade em Matemática. Nesse sentido, Gnedenko
(1982) salienta que o aluno será criativo em Matemática se ele gostar de matemática, algo que
11 raramente ocorre nas aulas. De tal forma, o Fator 1 foi denominado de Relação do Aluno com
a Matemática, apresentando índice alfa de Cronbach de 0,862. Como exemplo, podemos citar
os itens: “As aulas de Matemática estão entre minhas aulas preferidas” e “Eu acho fácil
aprender Matemática”.
O Fator 2 é composto por 16 itens e foi intitulado de Organização Pedagógica e
Criatividade Matemática. Apresentou alfa de Cronbach de 0,762 e diz respeito à percepção do
aluno quanto à forma como a professora organiza, planeja e desenvolve suas aulas de
Matemática e como ela insere o desenvolvimento da criatividade matemática do aluno nessa
organização pedagógica. Messias e Monteiro (2009) afirmam que as metodologias de ensinoaprendizagem utilizadas pelos professores em sala de aula poderão contribuir para a qualidade
do clima de sala de aula. Este fator contém, assim, itens que buscam avaliar a disponibilidade
de materiais e de espaços físicos no desenvolvimento das aulas e a variabilidade de ações
pedagógicas que podem estimular a elaboração de estratégias criativas de resolução de
problemas matemáticos. Exemplificando esse fator temos o item: “As aulas de Matemática
acontecem em vários lugares da escola (biblioteca, quadra de esportes, horta, pátio, etc.). ”
O fator 3 foi nomeado de Relação dos Colegas com a Matemática por abarcar 7 itens
que dizem respeito à percepção do aluno quanto à imagem que os colegas passam da
Matemática e do nível de criatividade desenvolvido nessa disciplina. O índice alfa de
Cronbach foi de 0, 731. Os itens “Meus colegas gostam das aulas de Matemática” e “Meus
colegas são criativos nas aulas de Matemática” exemplificam esse fator.
O fator 4 ficou constituído por 7 itens relacionados ao nível de apoio que a
professora dispensa à produção e comunicação de ideias pelo aluno. O fator ficou
denominado de Apoio da Professora à Produção e Comunicação de Ideias. Neste fator,
aborda-se a avaliação do aluno quanto à percepção que possui sobre o modo como a
professora desempenha seu papel de estimuladora de produção e comunicação de ideias
durante as aulas de matemática, ação docente que pode estimular o desenvolvimento do
potencial criativo dos alunos, na medida em que esses encontram espaço para aprimorar
quantitativa e qualitativamente a elaboração de ideias. O índice alfa de Cronbach foi de 0,664.
O seguinte item está presente nesse fator: “Nas aulas de Matemática a professora me dá tempo
suficiente para pensar sobre um problema que eu tenha que responder”.
O último fator, intitulado de Interações dos Alunos na Busca de Estratégias
Matemáticas, é constituído por 4 itens que buscam avaliar a forma em que se dão as
interações entre os alunos na sala de aula durante a resolução das atividades matemáticas.
Schoenfeld (2013) evidencia que os ambientes de aprendizado são altamente interativos.
12 Wigfield, Eccles & Rodriguez, (1998), citando Webb & Palincsar (1996), lembram que a
aprendizagem em sala de aula não se dá de forma isolada, mas sim por meio das
oportunidades e interações sociais em torno da aprendizagem. Neumann (2007) afirma que os
ambientes interativos são mais eficazes para fomentar a criatividade, pois as ideias criativas
são resultados das interações com os outros. Dessa forma, este fator se ocupa de mensurar o
quanto as interações entre os alunos são favoráveis à criação e comunicação de estratégias
matemáticas, uma vez que as ações conjuntas dos alunos podem favorecer o surgimento de
estratégias criativas. O índice alfa de Cronbach foi de 0,507. Mesmo o fator apresentando alfa
de Cronbach abaixo de 0.60, decidimos mantê-lo, pois este fator apresenta um aspecto
bastante lembrado na literatura sobre criatividade em matemática e sobre educação
matemática (SCHOENFELD, 2013; VALDÉS, 2010, NADJAFIKHAHA, YAFTIAN &
BAKHSHALIZADEH, 2012, NEUMANN, 2007; SAWYER, 2007; SIRIRAMAN, 2004). No
entanto, novas pesquisas com amostradas maiores e mais diversificadas e com a inclusão de
novos itens devem ser realizadas posteriormente para avaliar a importância desse fator para
avaliar o clima de sala de aula para criatividade em Matemática. Exemplificando esse fator
temos o seguinte item: “Meus colegas me procuram para eu ajudá-los nas atividades de
Matemática”.
Conclusão
Os resultados sugerem que o desenvolvimento integral das habilidades matemáticas
em sala de aula passa compulsoriamente pela confluência de múltiplos fatores se o que se
pretende é educar alunos proficientes em matemática. É claro que não se trata aqui de uma
matemática puramente lógica, mas, sobretudo, de uma matemática que possibilite ao
indivíduo o desenvolvimento integral de suas potencialidades, incluindo aqui a habilidade de
poder compreender seus processos de pensamento matemático e a habilidade de solucionar
problemas que exigem mais do que simples procedimentos algorítmicos.
Partindo dessa concepção, a elaboração da escala fundamentada na literatura que
sustente tal visão de educação matemática e validada por um rigoroso processo estatístico nos
permite ter em mãos um instrumento valioso no que diz respeito à avaliação do clima de sala
de aula. Professores, gestores, pesquisadores e os próprios alunos podem avaliar as
potencialidades e fragilidades que corroboram para a constituição do clima que pode
favorecer ou inibir o desenvolvimento das potencialidades criativas que cada aluno carrega.
Por fim, os dados conduzem à conclusão que o clima para criatividade nas aulas de
13 Matemática depende da confluência de cinco fatores: a relação do aluno com a Matemática, a
organização pedagógica em torno da criatividade matemática, a percepção sobre a relação dos
colegas com a Matemática, o apoio da professora à produção e comunicação de ideias e as
interações dos alunos na busca de estratégias matemáticas.
Recomendações
A versão completa da Escala de Clima para Criatividade em Matemática foi
elaborada para ser aplicada preferencialmente aos alunos matriculados no 5º ano do ensino
fundamental de escolas públicas e particulares, faixa de ensino na qual estavam matriculados
os alunos componentes da amostra de validação do instrumento. No entanto, estudos podem
ser orientados de modo a estender a escala para uso nas demais séries do ensino fundamental.
Recomenda-se, ainda, novos estudos no sentido de aprimorar a escala, seja ampliando a
amostra, seja realizando estudos nos quais o instrumento possa ser testado, principalmente em
relação ao fator Interações dos Alunos na Busca de Estratégias Matemáticas que apresentou
baixo valor de consistência interna.
A escala, em sua versão integral, tem potencial para servir de instrumento de
mensuração das percepções que o aluno faz sobre os fatores que interferem no modo como a
criatividade é tratada nas aulas de matemática, servindo de meio para que o professor possa
avaliar sua ação pedagógica em busca de favorecer o potencial criativo de seus alunos.
Referencial Teórico
ALENCAR, Eunice M. L. Soreano. Criatividade no contexto educacional: três décadas de pesquisa.
Psicologia: Teoria e Pesquisa, Brasília, v. 23, n. especial, p. 45-49. 2007
ALENCAR, Eunice. M. L. Soreano; FLEITH, Denise de Souza. Contribuições recentes ao estudo da
criatividade. Psicologia: Teoria e Pesquisa, Brasília, v. 19, n. 1, p. 1-8, jan./abril.2003.
AMBILE, Teresa M. The social psychological of creativity. NovaYork: Springer, 1983.
AMABILE, Teresa M. et al. Assessing the work environment for creativity. The Academy of
Management Journal, New York, v. 39, n. 5, p. 1154-1184, out. 1996.
CSIKSZENTMIHALYI, Mihaly. Creativity. New York: HaperCollins. 1996
FERNANDES, Luís Fernando de Pinho. Clima de sala de aula e Relação Educativa: as
representações dos alunos de 3º ciclo. 2008. 116 f. Dissertação (Mestrado em Observação e Análise da
Relação Educativa) - Faculdade de Ciências Sociais e Humanas, Universidade do Algarve, Faro, 2008.
14 FLEITH, Denise de Souza. Avaliação do clima para criatividade em sala de aula. In:ALENCAR,
Eunice M. L. Soreano; BRUNO-FARIA, Maria de Fátima; FLEITH, Denise de Souza (Orgs.).
Medidas de criatividade: teoria e prática. Porto Alegre: Armed, 2010.
FLEITH, Denise de Souza e ALENCAR, Eunice. M. L.Soreano.. Escala sobre o clima para
criatividade em sala de aula. Psicologia: Teoria e Pesquisa, v. 21, p. 85-91. 2005.
GNEDENKO, B.V. Sobre la creatividad Matemática. In: Gnedenko B.V. Formación de la
Concepción del mundo en los estudiantes en el proceso de enseñanza de La Matemática.
Colección Biblioteca del Maestro, Moscol, p. 94-106. 1982.
GONTIJO, Cleyton Hércules. Relações entre criatividade, criatividade em matemática e
motivação em matemática de alunos do ensino médio. 2007. 198 f. Tese (Doutorado em Psicologia)
– Instituto de Psicologia, Universidade de Brasília, Brasília. 2007.
GORSUCH, R. L. Factor analysis (2nd ed.). Hillsdale, NJ: Lawrence Erlbaum Associates. 1983.
HADAMARD, Jacques. Psicologia da invenção na Matemática. Tradução: Estela dos Santos
Abreu. Rio de Janeiro: Contraponto, 2009.
HALADYNA, Tom; SHAUGHNESSY, Joan; SHAUGHNESSY, J. Michael. A causal analysis of
attitude toward mathematics. Journal for Research in Mathematics Education, Washington, v. 14,
n. 1, p. 19-29. 1983.
HASHIMOTO, Yoshihiko. The Methods of fostering creativity mathematical through problem
solving.International Journal on Mathematics Education - ZDM, v. 29, n. 3, p. 86-87, jun. 1997.
HAYLOCK, Derek. Recognising Mathematical Creativity in Schoolchildren. International Journal
on Mathematics Education-ZDM,v. 29, n. 3, p. 68-74,jun. 1997.
KATTOU, Maria; KONTOYIANNI, Katerina; PITTA-PANTAZI, D Demetra; CHRISTOU,
Constantino. Connecting mathematical creativity to mathematical ability. ZDM Mathematics
Education, v. 45, p. 167-181. 2013.
KRUTETSKII, Vadim, A. The Psychology of Mathematical Abilities in Schoolchildren. Chicago:
The University of Chicago Press, 1976.
LUBART, Todd. Psicologia da criatividade. Tradução: Márcia Conceição Machado Moraes. Porto
Alegre: Artmed, 2007.
MAROCO, João; GARCIA-MARQUES, Teresa. Qual a fiabilidade do alfa de Cronbach? Questões
antigas e soluções modernas? Laboratório de Psicologia, v. 4, n. 1, p. 65-90. 2006
MESSIAS, Daniela; MONTEIRO, Vera. A motivação para a matemática e o clima de sala de aula de
Matemática. Atas do X Congresso Internacional Galego-Português de Psicopedagogia, p. 40304045. Braga: Universidade do Minho, 2009
NADJAFIKHAH, Mehdi; YAFTIAN, Narges; BAKHSHALIZADEH, Shahrnaz. Mathematical
creativity: some definitions and characteristics. Procedia - Social and Behavioral Sciences, v. 31, p.
285-29, 2012.
NEUMANN, C. J.. Fostering creativity. A model for developing a culture of collective creativity in
science. EMBO Reports, v. 8, n. 3, p. 202–206. 2007.
PASQUALI, Luiz. Psicometria: teoria e aplicações. Brasília: Editora Universidade de Brasília, 1997.
15 PASQUALI, Luiz. Testes referentes a construto: teoria e modelo de construção. In: PASQUALI, Luiz
(Ed.). Instrumentos psicológicos: manual prático de elaboração. Brasília: LabPAM/IBAPP, 1999.
PASQUALI,
Luiz.
Histórico
dos
instrumentos
Psicológicos.
2010.
em:http://pt.scribd.com/doc/64819811/LUIS-PASQUALI. Acesso em: 13 set. 2013.
Disponível
PIGGOTT, Jennifer. Cultivating Creativity. Mathematics Teaching, v. 202, p. 3-7, 2007. Disponível
em http://nrich.maths.org/5784. Acesso em 26/02/2014.
RODRIGUEZ GARRAN, Noelia. El clima escolar. Revista Digital Innovacion e
Investigacion, v. 3, n. 7, mar. 2004. ISSN 1696-7208
SANTOS , Clementina de Jesus Alhinho dos. Clima escolar e participação docente: a opinião dos
professores da educação pré-escolar e do ensino básico. 2010. 214 f. Dissertação (Mestrado em
Ciências da Educação) – Faculdade de Psicologia e Ciências da Educação, Universidade de Coimbra,
Coimbra, 2010.
SCHMIDT, M., & Ĉagran, B. Classroom climate in regular primary school settings with children with
special needs. Educational Studies, v. 4, p. 361-372. 2006.
SCHOENFELD, Alan H. (2013). Reflections on Problem Solving Theory and Practice. The
Mathematics Enthusiast, California, v. 10, p. 9-34, 2013.
SIMONTON, D. K. Creativity, leadership, and chance. In Sternberg, R. J. (Org.). The nature of
creativity. Nova York: Cambridge University Press., p. 386-426, 1988
SRIRAMAN, Bharath. The characteristics of mathematical creativity. The Mathematics Educator,
14, n. 1, p. 19-34, 2004.
STERNBERG, Robert J.; LUBART, Todd. An Investment Theory of Creativity and its
development,Human. Development, Califórnia, v. 34, n. 1, p. 1-31. 1991.
VALDÉS, C. Eloy Artega. El Desarrollo de La Creatividad em La Educacion Matemática. Congresso
Iberamericano de Educacion: Metas 2021, Buenos Aires, set, 2010.
WIGFIELD, Allan; ECCLES, Jacquelynne S.; RODRIGUEZ, Daniel. The Development of
Children's Motivation in School Contexts. Review of Research in Education, v. 23, p. 73-118, 1998.
Disponível em http://pt.scribd.com/doc/221264982/Wigfield-­‐Eccles-­‐Rodriguez. Acesso em:
27/06/2013 10:54