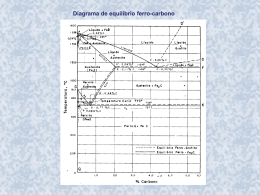
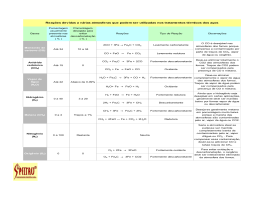
Diagramas de
Fases
Diagramas de Fases
Vamos tentar responder...
Quando nós combinamos dois elementos...
que estado de equilíbrio teremos?
• Em particular, se nós especificamos...
-- uma composição (por ex., %peso Cu - %peso Ni), e
-- uma temperatura (T )
então...
Quantas fases teremos?
Qual a composição de cada fase?
Quanto de cada fase teremos?
Fase A
Fase B
Ni
Cu
Limite de Solubilidade
Introdução
– Soluções –soluções sólidas , fase única
– Misturas – mais do que uma fase
Sucrose/Water Phase Diagram
• Limite de Solubilidade:
Questão: Qual o limite de
solubilidade a 20°C?
Temperature (°C)
Máxima concentração na qual
uma fase única ocorre.
100
Solubility
Limit
80
L
(liquid)
60
L
40
(liquid solution
i.e., syrup)
20
+
S
(solid
sugar)
Resposta: 65 %peso açucar.
20
40
60 65 80
100
Co =Composition (wt.% sugar)
Pure
Sugar
0
Pure
Water
se Co < 65 %p açúcar: xarope
se Co > 65 %p açúcar: xarope + açúcar
Componentes e Fases
• Componentes:
Elementos ou compostos que estão presentes em uma mistura
(por ex., Al e Cu)
• Fases:
Distinção física e química de regiões de um material
(por ex., α e β).
β ( fase clara)
Liga Al-Cu
α (fase escura)
Efeitos da Temperatura e da
Composição (Co)
• Mudando Temp pode mudar # de fases: de A para B.
• Mudando Co pode mudar # de fases: de B para D.
B (100°C,70%p) D (100°C,90%p)
Sistema Água - Açúcar
1 fase
Temperatura (°C)
100
2 fases
L
80
(liquido)
60
L
(Solução liquida
40
i.e., xarope)
+
S
(açúcar solido)
A (20°C,70%p)
20
2 fases
0
0
20
40
60 70 80
100
Co =Composição (%peso açúcar)
Equilíbrio de Fase
Sistema de solução Completa (por ex., Ni-Cu)
EletroEstrutura negatividade
r (nm)
Ni
FCC
1.9
0.1246
Cu
FCC
1.8
0.1278
• (Regra de W. Hume –Rothery) sugere alta solubilidade mutua.
• Ni e Cu são totalmente miscíveis em todas as proporções
5.2.1.
SOLUÇÕES SÓLIDAS EM METAIS
SOLUÇÕES SÓLIDAS SUBSTITUCIONAIS
• As soluções sólidas formam-se mais facilmente quando os
átomos do solvente e do soluto têm dimensões e estruturas
eletrônicas comparáveis.
• No caso do latão, o cobre e o zinco têm raios atômicos de
0,1278 e 0,1332 nm, respectivamente. Ambos têm,
excetuando-se o nível de valência, 28 elétrons e apresentam,
quando isolados, número de coordenação NC = 12. Portanto,
o zinco substitui facilmente até um máximo de cerca de 40%
dos átomos de cobre no reticulado CFC. Este é um exemplo
de solução sólida substitucional, bastante comum em vários
sistemas metálicos.
• Outro exemplo é a solução de cobre e níquel formando
o monel. Estas soluções vão desde praticamente a
ausência de níquel até quase 100% de átomos de
níquel. Todas as ligas cobre-níquel são CFC. Os raios
atômicos do cobre e do níquel são 0,1278 e 0,1246 nm,
respectivamente, e eles têm a mesma estrutura CFC.
• Por outro lado, há um limite muito bem definido na
quantidade de estanho que pode substituir cobre para
formar bronze e ainda manter a estrutura CFC do
cobre. O estanho em excesso, além da quantidade
correspondente à solubilidade sólida, forma uma outra
fase. Isto é definido pelo limite de solubilidade.
• Conforme aumenta a diferença de dimensões entre os
átomos, ocorre cada vez menos substituição. Apenas
20% dos átomos de Cu podem ser substituídos por
alumínio.
• Para ocorrer a completa miscibilidade em soluções sólidas
metálicas, os metais devem ser bastante similares, como
definido pela Regras de Hume-Rothery (metalurgista inglês,
1899-1968):
1) Menos que cerca de 15% de diferença nos raios atômicos
2) A mesma estrutura cristalina
3) Eletronegatividades similares (atração de elétrons)
4) A mesma valência.
• A Tabela 4-1 e a Figura 4-3 mostram a solubilidade sólida
máxima, no cobre, de vários metais com a mesma estrutura
CFC do cobre.
Diagrama de fases do sistema Cu-Sn
rCu = 0,1278 nm
rSn = 0,1509 nm
Diagrama de fases do sistema Cu-Al
rCu = 0,1278 nm
rAl = 0,1431 nm
Diagrama de fases do sistema Cu-Ni
rCu = 0,1278 nm
rNi = 0,1246 nm
Diagramas de Fases
• Indica as fases como função da Temperatura, Co, e P.
Neste curso:
- Sistemas binários: apenas 2 componentes.
- Variáveis independentes : Temperatura e Co (P = 1 atm).
1600
•Diagrama de Fases para o sistema Cu-Ni
Temperatura (°C)
1500
L (liquido)
• 2 Fases:
1400
L (liquido)
α (solução sólida CFC)
1300
α
1200
(solução sólida CFC)
1100
1000
0
Cu
20
40
60
%peso Ni
80
100
Ni
• 3 Campos de Fases:
L
L+α
α
Diagramas de Fases :
# e tipos de fases
• Regra 1: se conhecemos a Temp e a Co, então conhecemos:
-- o # e os tipos de fases presentes.
• Exemplos:
A(1100°C, 60%p):
α
1 fase:
1500
1400
oT(°C)
B(1250°C, 35%p):
2 fases: L + α
B (1250°C,35%p)
1600
1300
L (liquido)
α
1200
(ss CFC)
1100
1000
0
A (1100°C,60%p)
20
40
60
%peso Ni
80
100
Diagramas de Fases :
composição e fases
• Regra 2: se conhecemos a Temp e a Co, então conhecemos:
-- a composição de cada fase.
Sistema Cu-Ni
• Exemplos:
T D = 1190°C:
apenas Sólido ( α )
Cα = Co ( = 35 %peso Ni)
A
TA
1300
T(°C)
Co = 35 %peso Ni
TA = 1320°C:
apenas Líquido (L)
CL = Co ( = 35 %peso Ni)
L
B
TB
1200
D
TD
20
TB = 1250°C:
ambos α and L
CL = C liquidus ( = 32 %peso Ni )
Cα = C solidus ( = 43 %peso Ni )
α
30 32
35
CL Co
40
43
Cα
%peso Ni
50
Diagramas de Fases:
frações de fases
• Regra 3: se conhecemos a Temp e a Co, então conhecemos:
-- a quantidade de cada fase (%peso ou %mol).
• Exemplos:
Co = 35 %peso Ni
T(°C)
TA : apenas Líquido (L)
W L = 100 %peso, Wα = 0
TD: apenas Sólido ( α )
W L = 0, Wα = 100 %peso
T B : ambos α e L
43 − 35
= 73 %
43 − 32
WL =
S
R +S
Wα =
R
= 27 %
R +S
=
A
TA
1300
TB
1200
TD
20
L
B
R S
α
D
3032 35
CLCo
40 43
50
Cα %peso Ni
Regra da Alavanca
• Linha de interligação – conecta as fases em
equilíbrio – essencialmente numa isoterma
T(°C)
Quanto de cada fase?
Pense nisso como uma alavanca (gangorra)
L
1300
B
TB
Mα
ML
α
1200
R
20
S
30C C
40 C
α
L o
R
50
S
M α ⋅S = M L ⋅R
%peso Ni
WL =
C − C0
ML
S
=
= α
M L + M α R + S C α − CL
Wα =
C − CL
R
= 0
R + S C α − CL
Resfriamento em um sistema
binários: Cu-Ni
• Sistema é:
-- binário
i.e., 2 componentes:
Cu e Ni.
T(°C) L (liquid)
1300
L: 35 %p Ni
α: 46 %p Ni
--isomórfico
A
35
32
i.e., solubilidade
24
completa de um
componente no outro;
1200
o campo da fase α
estende-se de 0 to 100% Ni.
• Considerar
Co = 35 %pesoNi.
L: 35%pNi
110 0
20
B
C
46
43
D
L: 32 %p Ni
36
α: 43 %p Ni
E
L: 24 %p Ni
α: 36 %p Ni
α
(solid)
30
35
Co
40
50
%peso Ni
Sistemas em equilíbrio
• Cα no resfriamento.
• Cu-Ni : Primeira fase α a solidificar possui Cα = 46 %peso Ni.
Última fase α a solidificar possui Cα = 35 %peso Ni.
• Altas taxas de resfriamento:
estrutura em partes
• baixas taxas de resfriamento:
estrutura em equilíbrio
primeiro α
46 %peso Ni
último α
< 35 %peso Ni
Uniforme Cα:
35 %peso Ni
Propriedades Mecânicas:
Sistema Cu-Ni
• Efeito da solução sólida na resistência:
400
300
200
0 20 40 60 80 100
Cu
Ni
%peso Ni
-- Máximo em função de Co
--Ductilidade (%EL)
Elongamento (%EL)
Limite de Resistência (MPa)
-- Limite de Resistência (TS)
60
50
40
30
20
0 20
Cu
40
60
80 100
Ni
%peso Ni
-- Mínimo em função de Co
Sistemas Binários-Eutéticos
2 componentes
Possui uma composição com Temp de
fusão inferior aos componentes puros
T(°C)
Sistema Cu-Ag
1200
• 3 regiões com uma fase
L (liquid)
(L, α, β)
1000
• solubilidade Limitada :
α L + α 779°C
α: rico em Cu
L+β β
800
TE
8.0
71.9 91.2
β: rico em Ag
600
• TE : mínima Temp de fusão
α+β
• CE : Composição em TE
400
• Transição Eutética
L(CE)
α(CαE) + β(CβE)
200
0
20
40
60 CE 80
100
Co , %peso Ag
Diagrama de fases do sistema Ag-Cu
rCu = 0,1278 nm
rAg = 0,1444 nm
Diagrama de fases do sistema Cu-Pb
rCu = 0,1278 nm
rPb = 0,1750 nm
EX: Sistema Eutético Pb-Sn
• Para uma liga com 40 %p Sn – 60 %p Pb a 150°C, temos...
-- fases presentes: α + β
T(°C)
--composição das fases:
CO = 40 %peso Sn
Cα = 11 %peso Sn
Cβ = 99 %peso Sn
-- Qtde de cada fase:
Wα =
C - CO
S
= β
R+S
Cβ - Cα
59
99 - 40
=
= 67 %
88
99 - 11
C - Cα
Wβ = R = O
Cβ - Cα
R+S
40 - 11
29
=
= 33 %
=
99 - 11
88
300
200
L (liquid)
α
L+ α
18.3
150
100
L+β β
183°C
61.9
R
97.8
S
α+β
=
0 11 20
Cα
40
Co
60
80
99100
Cβ
C, %peso Sn
EX: Sistema Eutético Pb-Sn
• Para uma liga com 40 %p Sn – 60 %p Pb a 220°C, temos...
-- fases presentes : α + L
T(°C)
-- composição das fases :
CO = 40 %peso Sn
Cα = 17 %peso Sn
CL = 46 %peso Sn
-- Qtde de cada fase :
CL - CO
46 - 40
=
Wα =
CL - Cα
46 - 17
6
=
= 21 %
29
CO - Cα
23
=
WL =
= 79 %
29
CL - Cα
300
α
220
200
L+α
R
L (liquido)
L+β β
S
183°C
100
α+β
0
17 20
Cα
40 46 60
Co CL
80
C, wt% Sn
100
Microestruturas em Sistemas
Eutéticos:
• Co < 2 %peso Sn
• Resultados:
-L
-L + α
-policristais de grãos α
i.e., apenas uma fase sólida.
T(°C)
L: Co %peso Sn
400
L
α
L
300
200
α
L+ α
TE
α: Co %peso Sn
100
α+ β
0
Co
10
20
30
Co, %peso Sn
2
(limite de solubilidade a Temp ambiente)
Microestruturas em Sistemas
Eutéticos:
• 2 %p Sn < Co < 18,3 %p Sn
• Resultados:
ƒ
ƒ
ƒ
ƒ
L
L+α
apenas α
finalmente duas fases
¾ α policristalino
¾ inclusões finas de fase β
L: Co %p Sn
T(°C)
400
L
L
α
300
L+α
α: Co %p Sn
α
200
TE
α
β
100
α+ β
0
10
2
20
Co
30
C , %p Sn
o
18,3
(limite solub. a TE)
Microstruturas em Sistemas
Eutéticos:
• Co = CE
• Resultados: microestrutura Eutética (estrutura lamelar)
-- camadas alternadas (lamelares) de cristais de α e β.
T(°C)
L: Co %peso Sn
300
Micrografia de microestrutura
eutética Pb-Sn
L
α
200
L+α
L+β β
183°C
TE
100
α+β
0
20
18,3
40
β: 97,8 %peso Sn
α: 18,3 %pesoSn
60
CE
61,9
80
100
97,8
C, %peso Sn
160 μm
Estrutura Eutética Lamelar
Microstruturas em Sistemas
Eutéticos:
• 18,3 %peso Sn < Co < 61,9 %peso Sn (hipoeutético)
• Resultados: cristais α e uma microestrutura eutética
• logo acima TE :
L: Co %peso Sn
T(°C)
300
L
α
L
α
200
α L
L+α
R
TE
L+ β
S
β
α+β
100
α primário
α eutético
β eutético
0
20
18,3
40
60
61,9
CL = 61,9 %p Sn
Wα = S = 50 %
R+S
WL = (1- Wα) = 50 %
• logo abaixo TE :
S
R
Cα = 18,3 %p Sn
80
100
97,8
Co, %peso Sn
Cα = 18,3 %peso Sn
Cβ = 97,8 %peso Sn
Wα = S = 73 %
R+S
Wβ = 27 %
Hipoeutético & Hipereutético
300
L
T(°C)
α
200
L+ α
L+β β
TE
(Sistema Pb-Sn)
α+β
100
0
hipoeutético: Co = 50 %p Sn
α
α
α
20
40
60
80
Co, %peso Sn
eutético
61,9
hipereutético: (apenas ilustração)
eutético: Co = 61,9 %p Sn
β
α α
β
α
175 μm
100
160 μm
eutético micro-constituinte
β
β β
β
Compostos Intermetálicos
Mg2Pb
Composto intermetálico forma uma linha – não uma área –
composição estequiométrica exata
Eutetóide & Peritético
• Eutético
L
cool
heat
α+β
• Eutetóide
S2
intermetallic compound
- cementite
S1+S3
γ
• Peritético
S1 + L
cool
heat
α + Fe3C
(727ºC)
S2
δ+L
cool
heat
γ
(1493ºC)
Eutetóide & Peritético
Diagrama Fase Cu-Zn
Transição Eutetóide δ
γ+ε
Transição Peritética γ + L
δ
Diagrama de fases do sistema Cu-Zn
rCu = 0,1278 nm
rZn = 0,1332 nm
Diagrama de Fase Ferro-Carbono (Fe-C)
• 2 pontos importantes
T(°C)
1600
-Eutetóide (B):
γ ⇒ α + Fe3C
L
1400
1200
γ +L
γ
(austenita)
γ γ
γ γ
1000
α
800
600
120 μm
Resultado: Perlita =
Camadas alternadas de
α de Fe3C
S
γ +Fe3C
727°C = Teutetóide
R
S
1
0.76
L+Fe3C
R
B
400
0
(Fe)
A
1148°C
2
3
α+Fe3C
4
5
6
Fe3C (cementita)
L ⇒ γ + Fe3C
δ
Ceutetóide
-Eutético (A):
6.7
4.30
Co, %peso C
Fe3C (cementita-dura)
α (ferrita - macia)
Aço Hipoeutetóide
T(°C)
1600
δ
L
1400
α
γ
γ
α
γ αγ
(Sistema Fe-C)
1000
800
γ + Fe3C
r s
727°C
αRS
w α =s/(r +s) 600
w γ =(1- wα )
400
0
α
(Fe)
perlita
L+Fe3C
1148°C
α + Fe3C
1
C0
w perlita = w γ
w α =S/(R+S)
w Fe3C =(1-w α )
perlita
2
3
4
5
6
Fe3C (cementita)
γ γ
γ γ
γ +L
γ
1200
(austenita)
0.76
γ γ
γ γ
6.7
Co , %peso C
100 μm
Aço Hipoeutetóide
Ferrita pre-eutetóide
Aço Hipereutetóide
T(°C)
1600
δ
L
Fe3C
γ
γ
γ +L
γ
1200
(austenita)
γ
γ
1000
γ γ
γ γ
r
800
w Fe3C =r/(r +s)
w γ =(1-w Fe3C )
s
α R
600
400
0
perlita(Fe)
L+Fe3C
1148°C
γ +Fe3C
0.76
γ
γ
γ
γ
(Sistema Fe-C)
S
1 Co
w perlita = w γ
w α =S/(R+S)
w Fe3C =(1-w α )
α +Fe3C
2
3
4
5
6
6.7
Co , %pesoC
60 μm
perlita
Fe3C (cementita)
1400
Aço Hipereutetóide
preeutetóide Fe3C
Aços ligados com mais elementos
Ti
Mo
Si
W
Cr
Mn
Ni
%peso de elementos de liga
• mudanças na Ceutetóide :
Ceutetóide (%pesoC)
T eutetóide (°C)
• Mudanças na Teutetóide
Ni
Cr
Si
Ti Mo
W
Mn
%peso de elementos de liga
Composição da escória em aços
•
•
•
•
A escória adicionada no Refino tem a função tanto de proteção térmica
(evitar perda de temperatura) quanto proteção atmosférica (evitar
reoxidação), mas também pode ter a função de captação de inclusões.
Os principais insumos de escórias são: cal (CaO), a fluorita (CaF2), a
alumina (Al2O3), o óxido de magnésio (MgO), ou mais recentemente
escórias pré-fundidas, escórias sintéticas em que, além da mistura
mecânica dos componentes, é realizada também uma pré-fusão.
A utilização única ou combinada destes compostos fica a cargo dos
engenheiros de processos, que são os responsáveis por desenhar o
roteiro a ser seguido. Normalmente, seguem os diagramas
quaternários CaO-Al2O3-SiO2-MgO, mas na prática são utilizados os
ternários da combinação destes elementos.
A composição da escória está diretamente ligada à formação de
inclusões. Deseja-se evitar escórias de alto ponto de fusão, sólidas,
com interação ruim com o aço, e pouca ou nenhuma captação de
inclusões. Busca-se portanto escórias líquidas nas temperaturas de
processamento (1550°C a 1650°C), com boa interação com o aço e que
preferencialmente captem inclusões.
Composição
da escória
em aços
Diagrama ternário em corte isotérmico e em vista tridimensional do sistema CaO-Al2O3SiO2, evidenciando a região de menor ponto de fusão (Dave Finkelnburg. How Glazes
Melt: In Search of the Elusive Eutectic. Ceramic Starts Daily. [Online] Dezembro 09, 2009.
http://ceramicartsdaily.org/wp-content/uploads/2009/11/ternary-diagram-large.jpg).