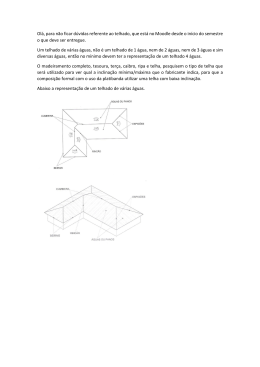
ISBN 978-85-8015-053-7
Cadernos PDE
VOLUME I I
Versão Online
2009
O PROFESSOR PDE E OS DESAFIOS
DA ESCOLA PÚBLICA PARANAENSE
Produção Didático-Pedagógica
ETNOMATEMÁTICA E A MATEMÁTICA DA
CONSTRUÇÃO CIVIL
CADERNO PEDAGÓGICO
O COTIDIANO DOS PEDREIROS E A
ETNOMATEMÁTICA
Fonte: Arquivo pessoal
ODETE BOING CHAVES
GOVERNO DO ESTADO DO PARANÁ
SECRETARIA DE EDUCAÇÃO DE ESTADO DO PARANÁ
NÚCLEO REGIONAL DE EDUCAÇÃO DE IVAIPORÃ
UNIVERSIDADE ESTADUAL DE LONDRINA
PROGRAMA DE DESENVOLVIMENTO EDUCACIONAL
ODETE BOING CHAVES
Área de Atuação
Matemática
Produção Didático-Pedagógica:
Caderno Pedagógico apresentada ao Programa
de
Desenvolvimento Educacional
(PDE)
da
Secretaria Estadual de Educação do Estado do
Paraná
sob
a
orientação
Doutor Túlio Oliveira de Carvalho
LONDRINA – 2009/2010
do Professor
“Subiu a construção como se fosse máquina.
Ergueu no patamar quatro paredes sólidas.
Tijolo por tijolo num desenho mágico. Seus
olhos embotados de cimento e lágrima”.
Chico Buarque
SUMÁRIO
Apresentação ................................................................................................................5
Problematização............................................................................................................6
Planta Baixa ..................................................................................................................6
O que é uma planta baixa .............................................................................................6
Atividade 1.....................................................................................................................7
Calculando Áreas ..........................................................................................................7
Atividade 2.....................................................................................................................8
Atividade 3.....................................................................................................................9
Calculando Perímetros..................................................................................................10
Atividade 4.....................................................................................................................11
Algumas Figuras Geométricas Planas ..........................................................................11
π
Que Número é Esse?...............................................................................................11
Eo
π ? O que significa?...............................................................................................12
O Teorema de Pitágoras ...............................................................................................12
Área do Triângulo..........................................................................................................13
Generalizando Áreas.....................................................................................................14
O Teorema de Pitágoras na Prática dos Pedreiros .......................................................14
Retas Perpendiculares ..................................................................................................14
Paredes Perpendiculares ..............................................................................................15
Atividade 5.....................................................................................................................16
A construção de Telhados.............................................................................................16
Atividade 6.....................................................................................................................20
Cálculo de Volume ........................................................................................................21
Alguns Exemplos de Sólidos Geométricos....................................................................22
Como medir um caminhão de areia ..............................................................................23
Atividade 7.....................................................................................................................24
Atividade 8.....................................................................................................................25
Atividade 9.....................................................................................................................25
Considerações Finais....................................................................................................27
Referências Bibliográficas .............................................................................................29
Apresentação
Quando passamos por uma casa, contemplamos e comentamos sobre o
quanto ela é admirável, mas não nos detemos para nos questionar como ela é
construída. O que esteia o teto? Como as paredes são tão alinhadas? Como é
edificado o telhado para evitar que a chuva entre? Como se acomodam tão
perfeitamente as portas e janelas? Qual o material necessário para levantar
uma casa? Qual é a matemática empregada nesta construção? Qual o número
de indivíduos envolvidos e como são esses indivíduos que constroem essa e
outros milhares de edificações que estão à nossa volta?
O fato é que nosso interesse está voltado tão somente para a estética de
uma construção, e não paramos para pensar sobre o que está por trás de tanta
imponência realizada por pessoas (em geral) simples, que, na maioria das
vezes, mal sabem interpretar os códigos da linguagem ensinados nos bancos
escolares, pessoas estas que muitas vezes passam despercebidos em nossa
sociedade.
Este trabalho tem, entre seus objetivos, incluir estas pessoas e apurar
seu conhecimento, particularmente na aplicação da matemática.
Para conhecermos tais pessoas e seu ofício, fez-se necessário uma
coleta de dados, numa empresa da construção civil da cidade de Ivaiporã, aqui
denominada L.A.D. Foi realizada através de procedimento etnográfico e
envolveu pedreiros, serventes e o mestre-de-obras.
A
análise
qualitativa
das
informações
encaminhou
nossos
questionamentos, como expomos a seguir. Foram analisados alguns aspectos
de maior interesse da pesquisadora como:
“Demarcação da planta baixa da casa (escala)”; “O Teorema de
Pitágoras”; “Volume”; “As paredes e a área dos tijolos”; “A inclinação do
telhado”; “A área das telhas e da cobertura”; “As portas e janelas da casa” e
“Os dois pisos da casa”. Estes aspectos contêm segredos matemáticos que
podem ser mais facilmente trazidos à tona, comprovando empiricamente os
conhecimentos
matemáticos
praticados
pelos
pedreiros
em
contexto
profissional.
5
Problematização:
• Como os pedreiros resolvem problemas matemáticos no exercício da sua
profissão?
• Que técnicas utilizam para resolverem problemas matemáticos em suas
profissões?
• Qual relação que evidencia a matemática ensinada nas escolas com a sua
prática?
• Prevalece uma desvinculação entre a matemática formal e a matemática
praticada no seu trabalho cotidiano?
Planta Baixa
Fonte: Arquivo pessoal
O que é uma planta baixa?
É o desenho de uma construção feito, em geral, a partir do corte
horizontal à altura de 1,5m a partir da base. É um diagrama dos
relacionamentos entre salas, espaços e outros aspectos físicos em um nível de
uma estrutura. Nela devem estar detalhadas em escala as medidas
das paredes, portas, janelas, o nome de cada ambiente e seu respectivo nível
6
Atividade 1
A foto da planta baixa apresentada na Figura acima representa o primeiro
piso de um sobrado de dois andares, nesta planta há uma cozinha, uma sala
de TV, um lavabo e a área de serviço. Observem-na, e responda as seguintes
questões:
Quais as formas geométricas presentes na planta?
O que significam os números na planta?
Como se traduzem estas informações da planta para o terreno?
Obviamente a planta da casa é menor do que a casa. Existe uma
proporção? Qual o nome você dá a esta proporção?
Há outros conceitos geométricos que você consegue visualizar na planta
baixa?
Calculando Áreas
Fonte: Arquivo pessoal
Na construção civil o cálculo de área é muito utilizado no revestimento
de pisos, cerâmicas, forro, laje, assoalhos, paredes, entre outros.
Na matemática utilizada na escola, temos que área é a medida de
superfície. A área de uma figura plana é obtida a partir da multiplicação em que
duas quantidades são essenciais: duas medidas de comprimento. Isto vale
para retângulos, mas ajuda também em triângulos.
7
Exemplo
Lajota
21cm
34cm
Fonte: Arquivo pessoal
Na figura acima temos uma lajota (semelhante a um pequeno tijolo, é
utilizada para assentar a laje, geralmente na construção de uma casa com mais
de um piso) de medidas 34 cm de comprimento por 21 cm de largura. Do
ponto de vista da área a ser coberta, estas são as medidas importantes na
lajota.
Para calcularmos a sua área, ou seja, a sua superfície, o que temos a
fazer é somente multiplicar essas duas quantidades:
A → área
A = 34x21
cm² → centímetro quadrado
A = 714cm²
Observem que a área tem unidade de comprimento ao quadrado.
Atividade 2
Assentamento de laje
1m
1m
Fonte: Arquivo pessoal
8
Na figura acima observamos a laje de um sobrado sendo assentada. De
acordo com a área de uma lajota (cálculo mostrado no exemplo), quantas
dessas lajotas são necessárias para recobrir uma área de 1 m²?
No assentamento, pode ser necessário quebrar algumas lajotas. Por
quê?
Durante
o
assentamento,
algumas
lajotas
podem
se
quebrar
involuntariamente. Como você faz o cálculo aproximado de modo que não
sobrem muitas, nem faltem lajotas no assentamento da laje?
É preferível sobrar ou faltar lajotas? Por quê?
Atividade 3
Tijolo de 6 furos
13cm
9cm
19cm
Fonte: Arquivo pessoal
A lateral de um tijolo de 6 furos (tijolo mais usado na construção civil)
possui 19cm de comprimento por 9cm de altura por 13cm de largura.
Parede construída
1m
1m
Fonte: Arquivo pessoal
As paredes são construídas com tijolos de 6 furos, com medidas
19x9x13 centímetros. As paredes externas são construídas com o lado do tijolo
que mede 19x9 centímetros.
9
Na figura acima, observamos uma parede externa construída com tijolos
de 6 furos, quantos tijolos de 6 furos são necessários para construir 1 m² de
parede?
Como calcular a quantidade de tijolos a serem comprados para construir
uma casa para que não falte e nem haja sobras desnecessárias?
Se as paredes internas forem construídas com a lateral do tijolo que
mede 13x19 centímetros, haverá alterações nos cálculos da quantidade de
tijolos a serem comprados?
Se houver alterações, o construtor comprará mais ou menos tijolos?
Qual a margem de sobra de tijolos entre as duas opções de construção
de paredes (externas e internas)?
Calculando Perímetros
No assentamento de piso o raciocínio de cálculo de área se repete, mas,
além do assentamento, existe um acabamento que se faz em todos os
cômodos, internamente, é a colocação de rodapé, uma espécie de arremate
que é necessário para que haja um arremate perfeito no piso. Esse contorno é
matematicamente chamado de perímetro.
As medidas de perímetro, área e volume são parte do cotidiano dos
pedreiros. Medir é comparar. A distância, por exemplo, pode ser medida com
passos, como fazem os pedreiros, que muitas vezes, para estimar
comprimentos, medem um comprimento com os próprios passos, utilizando o
metro somente quando necessitavam medir algo com precisão. Os pedreiros
têm a capacidade de realizar estimativas e cálculos aproximados e utilizá-los
na verificação de resultados de operações matemáticas.
Na discussão dos conceitos de perímetro, área e volume, a escolha da
unidade de medida é fundamental, e também a distinção entre as medidas
linear (perímetro), de superfície (área) e tridimensional (volume). Uma questão
que se coloca: como medir o contorno de uma sala, a superfície (o chão) da
sala? É usual trabalhar com o volume de um cômodo? Observamos que os
pedreiros utilizam muito o metro e o metro quadrado como medidas de
comprimento e área, embora também usem a medida de seus passos como
estimativa, quando querem medir comprimentos lineares, em que cada um
desses passos equivale a um metro.
10
Atividade 4
A partir dos conceitos acima, como estimar o perímetro de uma sala
retangular?
Se for preciso cercar o terreno, como saber seu perímetro?
Formas circulares são menos usadas em construções, mas muitas
vezes elas aparecem. Como calcular o seu perímetro?
Nos cálculos de área e perímetro na escola, temos o auxílio das
chamadas representações de figuras planas, sendo as mais comuns as que
reproduzimos abaixo:
Algumas Figuras Geométricas Planas
quadrado
retângulo
losango
paralelogramo
triângulo
círculo
π (pi) Que Número é Esse?
Com uma corda esticada e uma estaca amarrada em cada uma das
extremidades, é simples demarcar uma circunferência no chão para a
construção de um poço, uma fossa, uma piscina ou uma construção circular
qualquer. O esquema abaixo mostra como isso é possível:
estacas
.
.
Corda
11
Fincada uma das estacas no chão, o pedreiro estica a corda e roda a
outra estaca em volta sempre com a corda muito bem esticada ele obtém o
desenho de um círculo no chão.
Será que os pedreiros conseguem fazer construções ou estruturas
circulares sem alguma vez terem ouvido falar do
π,
isto é, sem saber o que
este número irracional representa?
As partes da circunferência são:
•
A corda esticada representa o raio, ou seja, a metade do diâmetro;
•
A estaca central representa o centro;
•
O desenho obtido é a circunferência, e seu perímetro é proporcional a
π.
E o π? O que significa?
É comprimento da circunferência e dividido pelo seu diâmetro, isto é,
aproximadamente 3,14. Os gregos antigos tinham a estimativa
π=22/7.
Será
que nossos pedreiros conhecem esta estimativa?
Para calcular o perímetro ou a área de uma figura plana circular sempre
nos utilizaremos do valor do π (pi).
Em sua prática, o pedreiro diz que não é necessário fazer cálculos,
basta medir quatro diâmetros e multiplicar pelo próprio diâmetro e pode-se
saber mais ou menos o comprimento de um circulo, e se quiser saber com
mais exatidão, é só tirar 20% do quarto diâmetro, e proceder ao mesmo
cálculo.
Ao ser questionado como se chega neste valor, não argumenta, apenas
atribui o cálculo à experiência. Uma atividade interessante é determinar se este
procedimento fornece uma boa aproximação.
O Teorema de Pitágoras
O Teorema
de
Pitágoras
é
provavelmente
o
mais
célebre
dos teoremas da matemática. Enunciado pela primeira vez por filósofos gregos
chamados de pitagóricos, estabelece uma relação simples entre o comprimento
dos lados de um triângulo retângulo:
12
Em qualquer triângulo retângulo, o quadrado da hipotenusa é igual à
soma dos quadrados dos catetos.
Fonte: http://www.diaadia.pr.gov.br/tvpendrive
Se a designar o comprimento da hipotenusa e b e c os comprimentos
dos catetos, o teorema afirma que:
a² = b² + c²
Área do Triângulo
Na área de um triângulo qualquer, muitas vezes não temos de imediato
a medida de sua altura, pois ela só poderá ser determinada se houver um
ângulo reto, ou seja um dos ângulos deverá medir 90 0 (noventa graus), por
isso, devemos calcular esta altura da seguinte forma:
x
x
x
h
x
x
2
Para calcular, traçamos uma reta (pontilhado da segunda figura, é a sua
altura h), até a base do triângulo de forma que forme um ângulo reto na base, a
partir de então utilizamo-nos do Teorema de Pitágoras.
13
Portanto, concluímos que:
x
h
A∆ =
bh
2
x
2
Generalizando Áreas:
Para o cálculo de área de quase todas as figuras geométricas planas,
basicamente multiplicamos as medidas das medidas do comprimento (base) e
da largura (altura) da mesma e para o cálculo de perímetro, somamos todos os
comprimentos dos lados da figura.
O Teorema de Pitágoras na Prática dos Pedreiros
Ao perguntar aos pedreiros se conhecem o Teorema de Pitágoras,
provavelmente responderão que não, como a resposta que ouvi de um
servente de pedreiro da obra:
”Eu sei que sou bom de matemática, não me lembro das
fórmulas que ensinaram na escola, as contas que faço,
faço de cabeça, são menos complicadas do que as que
aprendi na escola, não uso calculadora porque não
gosto de trabalhar com ela, na cabeça é mais rápido.”
Mas mesmo sem esse conhecimento, eles fazem uso do mesmo em
vários momentos do seu trabalho, como podemos observar na figura abaixo,
duas paredes só serão perpendiculares se o ângulo que se forma quando elas
se “encontram” mede 90º.
Retas Perpendiculares
Retas Perpendiculares são duas retas que se cruzam, formando ângulos
de 90 graus.
14
Paredes perpendiculares
Fonte: Arquivo pessoal
No seu trabalho diário, os pedreiros medem regularmente ângulos retos
(90º). Estes ângulos tanto podem ser medidos em grandes paredes como em
paredes com pequenas dimensões. Às vezes, os pedreiros usam como
modelo, para medir um ângulo de 90º um azulejo porque sabem que ele
contém quatro ângulos de 90º exatamente iguais; mas quase sempre usam um
esquadro (muitas vezes construído por eles mesmos) para garantir que as
paredes estão ou não no esquadro (retas), isto é, garantir que dois planos
fiquem
perpendiculares
entre
si, formando
ângulos
retos, o
que
é
imprescindível em qualquer construção, é também usado o mesmo processo
nas divisões com uma forma retangular, quadrada, como as divisões internas
dos cômodos da construção.
Os ternos pitagóricos são triplas de números naturais a, b e c, de modo
que a²+b²=c². O fato de obedecerem a esta relação implica que a, b e c são
lados de um triângulo retângulo, e que c é o maior lado.
Há duas atividades possíveis: sorteie seqüências de três números para grupos
e peça que verifiquem
(a) se podem ser medidas de lados de um triângulo
(b) se o triângulo é retângulo
Outra atividade: com triângulos desenhados (alguns retângulos, outros
não), peça para medirem com régua os lados, possivelmente transformando
por alguma escala. O ideal é que não se use régua milimetrada, mas
alguma medida de referência.
Os esquadros construídos pelos pedreiros seguem sempre um esquema
(um Terno Pitagórico), como representa as figuras abaixo:
15
50
30
60
100
40
80
Atividade 5
Sabendo que Retas Perpendiculares – São retas que se cruzam
formando um ângulo reto, ou seja, igual a 90° (noventa graus), conforme
mostram as figuras abaixo, dê as soluções possíveis para os problemas
apresentados.
a) Um construtor tem 100 metros de tela para delimitar um terreno de
forma retangular. Quais as dimensões do terreno para que a área cercada seja
máxima?
b) Um mestre de obras quer construir um recinto cujas paredes sejam
perpendiculares entre si. Para isso, deve colocar estacas nos vértices da área
a ser construída. Ele conta com apenas um barbante comprido. Como ele
poderia, utilizando o Teorema de Pitágoras, saber onde fincar as estacas?
A Construção de Telhados
Fonte: Arquivo pessoal
16
Existem telhados de diversas formas, de forma geral, são constituídos
pela composição de planos inclinados. Um dos mais simples é o telhado de
duas águas. Em geral, a cobertura é feita de telhas de barro, mas outros
materiais podem ser usados, como o alumínio e a argila. A inclinação de um
telhado corresponde às necessidades climáticas da região na qual é construído
e da cultura do lugar. Em regiões do Brasil com influência européia, por
exemplo, na região sul, o telhado possui cumeeira bem elevada, para que os
planos inclinem-se em ângulos superiores a 60 0 , o ângulo de inclinação de tal
telhado apenas se justifica por razões estéticas. Mas os mais comuns são os
telhados com ângulos de inclinação de 30 0 , o suficiente para o escoamento
das águas das chuvas.
Ao iniciar a construção do telhado, após escolher o tipo de telha, o
pedreiro deve calcular a porcentagem de inclinação do mesmo para a
montagem da “tesoura”. A tesoura é uma estrutura de madeira cuja vista
transversal é mostrada abaixo.
As vigas de madeira formam o desenho de vários triângulos. Muitos
deles são triângulos retângulos. Os triângulos são utilizados pelos pedreiros
devido ao fato de os mesmos serem polígonos que não possuem mobilidade, e
quanto mais triângulos as madeiras formarem no telhado, maior rigidez ele
terá.
Existem no mercado vários tipos de telhas, no cálculo da porcentagem
de inclinação do telhado, vamos usar como exemplo a telha DUPLAN, que
exige uma inclinação mínima de 30% para que a água da chuva possa escoar.
17
Telha Duplan
Fonte: www.ceramicasantamariaro.com.br
A inclinação de 60 0 é obtida pelo pedreiro partindo da extremidade para
o topo do telhado. Para cada metro (100 cm) na horizontal, sobe-se 30 cm.
Se a tesoura tiver 6 metros de comprimento o pedreiro efetua o cálculo
da porcentagem utilizando apenas a metade dessa medida, ou seja, 3 metros.
3m
Esse cálculo é efetuado mentalmente e de forma rápida pelo pedreiro,
multiplicando essa medida pela porcentagem relativa à inclinação do telhado.
Os dois últimos números do produto dessa multiplicação são os centímetros.
Veja o cálculo do pedreiro:
3m x 30%
⇒ tan600 ≅ 0,3
3m
Temos então as medidas dos dois catetos de um triângulo retângulo:
Comprimento = 3m
Altura = 3m x 30% = 0.9m
Podemos
então,
através
do
teorema
de
Pitágoras
calcular
o
comprimento da viga onde serão colocadas as telhas, ou seja, a hipotenusa do
triângulo retângulo.
Este é um exemplo que mostra como a Matemática Escolar é importante
para a resolução de problemas do cotidiano.
18
Observe nas figuras a seguir que o telhado apresenta várias partes em
sua montagem, além da tesoura.
Fonte: http://www.ebanataw.com.br/roberto/telhado/tlhcur9.htm
Depois de concluir o madeiramento, o pedreiro efetua o cálculo da
quantidade de telhas necessárias para cobrir o telhado. Para isso leva em
consideração a área útil de cada tipo de telha, ou seja, a área de cobertura real
da telha.
Cada telha Duplan tem um comprimento de 33,3 cm e uma largura de
20 cm. Observe que cada quinze telhas cobrem 1 m², como mostra a figura a
seguir.
1m
33,3cm
20cm
1m
Mesmo sabendo que 15 telhas cobrem 1 m², o pedreiro aumenta o
comprimento e a largura do telhado na hora de calcular a quantidade de telhas.
Ele utiliza múltiplos de 33,3 cm (comprimento da telha) e de 20 cm (largura da
telha), aproximando-se ao máximo da quantidade exata de telhas a serem
utilizadas na cobertura do telhado.
19
Exemplo
Para se calcular a quantidade de telhas necessárias para a cobertura,
multiplica-se a metragem do telhado pelo rendimento da telha por m²,
adicionando 5% que pela prática tornou-se uma regra para eventuais perdas
por quebra ou defeitos nas peças.
Exemplo: Metragem do telhado = 130 m²
Modelo escolhido: Telha Duplan = 15 peças cobrem 1 m²
130 m² x 15 peças = 1950 telhas (quantidade a ser comprada) + 5%.
Atividade 6
No cálculo da porcentagem de inclinação do telhado, cada telha
determina a inclinação mínima para que não haja problemas com a água das
chuvas.
TABELA DE INCLINAÇÃO DE TELHADOS
TIPO DE TELHA
RAZÃO %
ÂNGULO APROXIMADO
Colonial
25 a 45
19 0
Telhão
20 a 45
18 0
Capanal
30 a 50
22 0
Paulistinha
25 a 45
19 0
Plana
100
45 0
Germânica
42 a 60
27 0
Plan
20 a 45
13 0
Romana
30 a 45
21 0
Francesa
30 a 45
21 0
Calcular para cada tipo de telha da tabela acima a altura da tesoura de
um telhado com base de 8 m de comprimento, conforme figura abaixo.
20
8m
Cálculo de Volume
Fonte: Arquivo pessoal
Na experiência com construção civil, é muito importante a distinção entre
volume e capacidade. A capacidade de um recinto corresponde ao volume em
seu interior. O volume ocupado é, considerando a largura das paredes, um
pouco maior. Esta diferença também aparece em regiões planas. Por exemplo,
quando se compra um terreno de 300 metros quadrados, a área máxima de um
piso de uma casa, levando em conta apenas a largura das paredes é um pouco
menor. No caso de existirem leis no município obrigando os moradores a
deixarem um vão livre, sem construção de paredes internas, na fronteira do
terreno, a área útil é ainda menor.
Ao questionarmos um pedreiro sobre como ele calcula quanto
argamassa é necessária para construir os pilares de uma obra, a resposta é o
que esperamos ouvir:
“Primeiro eu preciso saber as medidas, tenho
que medir o comprimento, a largura e a altura,
depois eu só multiplico”.
21
c
V = a.b.c
b
a
Na matemática escolar, o volume de um corpo pode ser calculado pelo
produto da área da base pela medida da altura. De uma forma geral, podemos
aplicar a seguinte fórmula:
V = a.b.c,
Onde:
V representa volume;
a.b representa a área da base;
c representa a altura.
De acordo como Sistema Internacional de medidas (SI), o metro cúbico
é a unidade padrão das medidas de volume. Um metro cúbico (1m³)
corresponde a uma capacidade de 1000 litros. Essa relação pode ser
exemplificada em conjunto com a Geometria, através de um cubo com arestas
medindo 1 metro.
1m
1m
1m
Alguns Exemplos de Sólidos Geométricos
Fonte: http://www.diaadia.pr.gov.br/tvpendrive
22
Cubo
Cilindro
Fonte: Arquivo Pessoal
Cone
Como medir um caminhão de areia?*
Quando se compra a areia com a condição de pagar somente o que for
efetivamente entregue, é preciso fazer a medição do caminhão em obra. A
medição é feita enfiando-se um ferro de construção no monte de areia, antes
dela ser descarregada. Deve-se também medir as dimensões internas da
caçamba (comprimento e largura).
As medidas com o ferro de construção devem ser feitas em cinco pontos
estratégicos, a saber -- no centro do monte (parte mais alta) e em cada um dos
cantos (vide figura abaixo).
Fonte: http://www.forumdaconstrucao.com.br
O volume será a média das alturas, multiplicado pela largura e pelo
comprimento da caçamba. Como demonstrado abaixo:
 M1 + M 2 + M3 + M4 + M5 
V = 
xLxC
5


Sendo:
V, o volume;
M1, M2, M3, M4 e M5, as medidas verificadas pelo pedreiro;
L, a largura da caçamba;
C, o comprimento da caçamba.
23
Atividade 7
Esta atividade deverá ser realizada pelos alunos, que se deslocarão até
uma construção e farão uma pesquisa de campo.
Sabe-se que em uma construção muitas vezes há a necessidade de
aterramento, e para isso, são contratados caminhões para transportar toda
terra a ser utilizada. Os alunos, de posse de seu material deverão, em grupos,
se dirigirem até o local onde houver uma construção e buscarão todas as
informações que julgarem necessárias para desenvolverem a atividade abaixo:
Fonte: Arquivo pessoal
1. Na obra em questão, houve ou haverá necessidade de aterramento?
2. Se o aterramento é necessário, como é feito?
3. Como saber a quantidade de terra necessária?
4. Como é comprada a terra?
5. Se há a necessidade do transporte em caminhões basculantes,
coletar os dados com os pedreiros para calcular o volume da terra
transportada pelo caminhão.
6. Há essa mesma lógica na medida de volume de outros materiais
como areia ou brita?
7. O pedreiro precisa saber calcular volume? Há relação entre o volume
calculado na obra e o volume calculado na escola?
24
Atividade 8
Na figura abaixo estão representados três degraus iguais de uma
escada de cimento. Cada degrau é um prisma triangular com as dimensões
indicadas:
Considere uma escada com 20 degraus idênticos aos da figura. Obtenha
o volume de concreto necessário para construí-la.
Atividade 9
Fonte: Arquivo pessoal
25
Em uma construção são necessárias 8 colunas de concreto para
sustentar o segundo piso, cada coluna tem a base quadrada de 20cmx20cm e
com altura de 3m. Obtenha o volume em metros cúbicos para o gasto de
concreto para as 8 colunas.
26
Considerações Finais
A sociedade atual está em constante mudança, a cidadania e a
matemática
são
consideradas
temas
fundamentais
na
educação.
É
imprescindível que as pessoas, no seu cotidiano utilizem conhecimentos
matemáticos, não só para a compreensão do mundo que as rodeia, mas
também como meio facilitador de relação social e desenvolvimento de sua
civilidade. Tal atitude pode contribuir para a mudança social, especificamente
na justiça, na inclusão e na solidariedade.
Ao pesquisar os profissionais da construção civil, apesar de observar
que a grande maioria possui baixa escolaridade, percebi que desenvolveram
capacidade para certos cálculos matemáticos ao longo da vida, acumulando
estes esquemas através da experiência profissional e de conhecimentos que
os mais antigos lhes ensinaram. Isto não sugere que estes conhecimentos e
processos matemáticos, que não foram aprendidos na escola, mas em
contexto profissional, não tenham uma forte ligação com a matemática que se
aprende e se ensina nas escolas.
No trabalho aqui desenvolvido, percebemos que o conhecimento
matemático dos pedreiros em sua profissão pode e deve interagir com o
conhecimento matemático escolar. É neste sentido que se compreende a
matemática como saber universalmente construído, incluindo ali o cotidiano
das profissões.
O mais interessante na prática profissional dos pedreiros, é que a
matemática não é isolada e sim englobada no contexto de suas atividades, não
se desvinculam os cálculos, eles emergem no ambiente de trabalho de uma
forma natural, sem perder a essência. É considerado um bom pedreiro aquele
que utiliza cálculos matemáticos que solucionem os problemas que surgem no
decorrer de sua atividade. Percebe-se que na atividade diária dos pedreiros,
mesmo que de forma empírica, estão implícitos os mais diversos conteúdos
escolares, tais como simetria, geometria, trigonometria, e principalmente os
procedimentos de cálculo.
Concluímos que a matemática escolar pode ser relacionada com a
matemática praticada no cotidiano do grupo envolvido, e que a Etnomatemática
está diretamente ligada ao contexto do trabalho, e deve contribuir para o
desenvolvimento dos estudantes, tornando-os capazes de reconhecer que a
27
matemática por eles aprendida no âmbito escolar é a mesma utilizada nas
práticas sociais. Tudo isso só servirá se conseguirmos com que os alunos
percebam na matemática uma via para melhor viverem em sociedade,
desenvolvendo a sua criatividade e tornando-se cidadãos críticos e
conscientes.
28
REFERÊNCIAS BIBLIOGRÁFICAS
D’AMBRÓSIO, U. Etnomatemática. Elo entre as tradições e a
modernidade. Coleção Tendências em Educação Matemática. 2ª
Edição. Belo Horizonte, Autêntica, 2002.
_____. – Curso: Um Olhar Etnomatemático para a Educação Matemática,
2001, disponível em:
<http://www.fe.unb.br/etnomatematica> - Acesso em 16/02/2010 às
10h55min
_____. - Etnomatemática. São Paulo: Ática, 1990.
KNIJNIK, Gelsa, et al, Organizadores. Etnomatemática Currículo e
Formação de Professores. Santa Cruz do Sul: Edunisc, 2004.
PARANÁ. Diretrizes Curriculares da Educação Básica: Matemática,
Secretaria de Estado da Educação do Paraná, 2008.
Imagens disponíveis em:
<Arquivo Pessoal da Autora>
<http://www.diaadia.pr.gov.br/tvpendrive> - Acesso em 05/04/2010 às
13h12min
<www.ceramicasantamariaro.com.br> - Acesso em 05/04/2010 às
13h34min
< http://www.ebanataw.com.br> - Acesso em 06/04/2010 às 09h
<http://www.forumdaconstrucao.com.br> - Acesso em 05/07/2010 às 13h
29