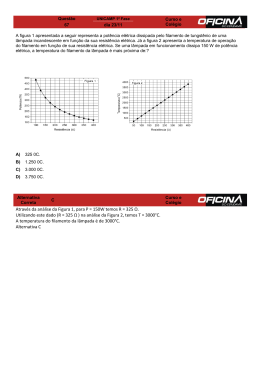
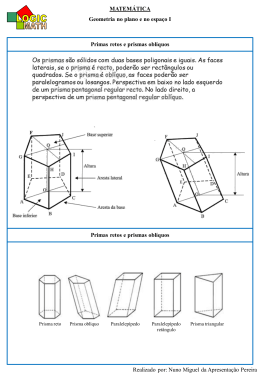
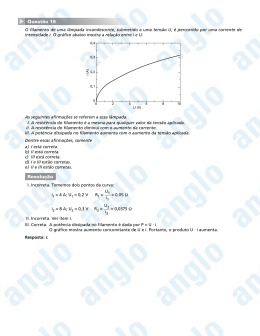
Estrutura da Matéria
2005/2006
Espectroscopia de emissão/absorção com espectrómetro de prisma
Objectivo:
•
•
Estudar o espectro de emissão de um sólido incandescente (filamento de tungsténio);
Registar e interpretar os espectros de absorção de várias amostras.
Material necessário:
1. Espectrómetro de prisma, Pasco mod.
OS-8539;
2. Suporte para prisma, Pasco, mod. OS8543;
3. Prisma;
4. Lâmpada de tungsténio, Pasco OS-8542
(Vmax = 10V);
5. Fonte de alimentação DC, 0-10V;
6. Sensor de infravermelhos, Pasco mod.
CI-6628;
7. Interface Pasco 7500
8. PC com programa “Science
Workshop”;
9. 2 multímetros;
Fig. 1 – Esquema do espectrómetro de prisma e
percurso da luz através dele.
A luz emitida pela lâmpada de tungsténio passa
através de uma fenda e incide numa lente que
transforma o feixe de luz incidente num feixe de
raios paralelos. A luz atravessa então o prisma
que deve ser posicionado conforme indica a Fig.
2, e é refractada segundo um ângulo que depende
do comprimento de onda da luz incidente. A luz
refractada pelo prisma passa então por uma
segunda lente e é detectada por sensor de luz
(fotómetro), que está colocado no plano focal da
Sensor de
rotação
2ª lente. Esta lente e o fotómetro estão montados
sobre um suporte que pode rodar em torno de um
Fig. 2 – Montagem do prisma e do
eixo, permitindo a medição da intensidade da luz
fotómetro na mesa do espectrómetro.
refractada em função do ângulo de refracção. O
suporte do prisma está fixo. O sensor de luz e o sensor de rotação do suporte do fotómetro estão
ligados a um computador através de uma interface Pasco 7500.
1. Prisma e refracção da luz:
O prisma utilizado é um prisma de vidro,
de 60º, cujas faces têm 20 mm × 20 mm.
O prisma é colocado de forma que o feixe
incidente incida conforme se indica na
Fig. 3, ou seja, perpendicularmente ao
segundo dioptro. Desta forma o ângulo de
incidência é θ1 = 60º e
φ
θ2
θ2 + θ3 = 60º
θ4
θ3
θ1
Aplicando a lei de Snell a cada uma das
faces do prisma obtêm-se as seguintes
relações:
φ
nar sen 60º= nv sen θ2
Fig. 3 – Esquema do prisma (φ = 60º).
nv sen θ3 = nar sen θ4
Ou seja,
sen θ2 =
sen θ2 =
1
nv
3
2
nv sen ( 60º−θ2 ) = sen θ4
1 3
nv 2
1 3
cos θ2 = 1 −
n v2 4
ou
1/ 2
nv ( sen 60ºcos θ2 − cos 60ºsenθ2 ) = sen θ4
Substituindo na 3ª equação o sen θ2 e cos θ2 pelas suas expressões, vem que
nv
3
1 3
1−
2
n v2 4
1/ 2
−
1 1 3
= sen θ4
2 nv 2
nv 2 −
e
3
4
1/ 2
=
2
1
sen θ4 +
2
3
i.e.,
nv =
2
1
sen θ4 +
2
3
2
+
3
4
(1)
A dependência do índice de refracção com o comprimento de onda é dade pela equação de Cauchy
n( λ ) = A +
B
λ2
(2)
em que A e B são constantes que dependem do tipo de vidro de que é feito o prisma. Para este
prisma A = 1,689 e B = 13900 nm-2 (ver apêndice I).
2. Lâmpada de tungsténio [1-3]:
2. 1 Teoria:
O filamento da lâmpada (de incandescência) utilizada é de tungsténio e quando é percorrido por
uma corrente eléctrica aquece, emitindo radiação cuja intensidade depende da temperatura do
filamento, de acordo com a lei de Stefan-Boltzmann:
R = A ε σ T 4 (W)
em que Α é a área do corpo emissor, ε a emissividade do tungsténio, σ = 5,67×10-8 W/(m2.K4) a
constante de Stefan-Boltzmann e T é a temperatura absoluta. A energia emitida por unidade de área
e por unidade de tempo entre λ e λ+dλ é dada pela expressão
c
R( λ )dλ = ε λ ρ ( λ )dλ
4
em que ρ(λ) representa a densidade de potência
emitida por um corpo negro e é dada pela lei da
radiação de Planck (Fig.4):
ρ ( λ )dλ =
8π hc
ρ(λ)
dλ
λ 5 e hc/ λ kT − 1
O comprimento de onda para o qual a intensidade
da radiação é máxima obedece à lei de
deslocamento de Wien,
1
λmaxT = 2,898×10-3 m/K
Fig. 4 – Densidade de potência emitida por
um corpo negro para várias temperaturas1.
2.2 Determinação da temperatura do filamento:
Para pequenas variações de temperatura pode-se considerar que a resistência de um condutor varia
linearmente com ∆T de acordo com a expressão:
R(T ) = R0 [1 + α (T - T0 )]
120
em que R0 é a resistência a uma dada temperatura de
referência T0, α é o coeficiente de temperatura da
resistividade do filamento.
Para grandes variações de temperatura, como α depende
da temperatura, a relação anterior não é válida (Fig.5).
Na tabela 2 do Apêndice I estão reunidos os valores da
resistividade do tungsténio para temperaturas
compreendidas entre 300 e 3600 K. Representando
graficamente a relação ρ/ρ0 em função de T-T0 (com
80
1
http://hyperphysics.phy-astr.gsu.edu/hbase/bbrc.html
ρ (µΩ .cm)
100
60
40
20
0
0
500
1000
1500
2000
2500
3000
3500
4000
T (K)
Fig. 5 – Variação da resistividade do
tungsténio com a temperatura.
T0=300 K), verifica-se que ρ/ρ0 e, portanto, R/R0 varia quadraticamente com (T-T0) de acordo com
a relação
R
= 1 + α (T - T0 ) + β (T - T0 ) 2
(3)
R0
em que α e β são parâmetros ajustáveis (ver Fig.2 do apêndice I). Uma vez conhecida a resistência
do filamento a uma temperatura de referência, pode-se determinar a temperatura do filamento
quando ele é atravessado por uma dada corrente I, medindo a sua resistência. Para tal tem de se
incluir no circuito de alimentação da lâmpada, um amperímetro para medir a corrente no circuito e
um voltímetro para medir a diferença de potencial entre os terminais da lâmpada.
2.3 Tensão de alimentação da lâmpada de tungsténio (Pasco, mod. OS-8542):
A diferença de potencial entre os terminais da lâmpada de tungsténio utilizada pode variar entre 0 e
10 V, mas o valor recomendado é de 7 V.
3. Fotómetro – sensor de infravermelho Pasco, mod. CI-6628 (ver ref. 5) ;
Procedimento experimental
1. Monte o circuito de alimentação da lâmpada
de tungsténio;
2. Determine a resistência do filamento à
temperatura ambiente;
3. Ligue o interface PASCO 7500;
4. Ligue o computador e inicialize o programa
Science Workshop;
5. Ligue o fotómetro a uma das entradas
analógicas do interface Pasco 7500;
6. Ligue o sensor de rotação a uma das entradas digitais do interface Pasco 7500 e seleccione
1440 div/rot;
7. Em “sampling options” escolha uma frequência de amostragem de 20 Hz.
8. Seleccione o modo “graph” para representar os valores recolhidos.
Resolução angular:
O eixo do sensor de rotação roda cerca de 60 vezes para cada rotação da placa graduada (360º).
Uma rotação do eixo do sensor representa 6º de deslocamento da placa graduada. Como a resolução
do sensor é de 1440 div/rot, e uma rotação do eixo do sensor corresponde a 6º, a resolução angular
das medidas é de 6/1440 = 4,167 × 10-3º = 0,25’ = 15’’ = 7,272 × 10-5 rad.
a) Registo de um espectro de emissão do filamento de tungsténio:
- Ligue a lâmpada de tungsténio (~7 V);
- Registe o valor da intensidade da corrente que percorre o filamento e a diferença de potencial
aplicada.
- Rode o suporte do fotómetro até que o sensor esteja alinhado com a direcção do feixe incidente;
- Bloqueie o feixe de luz , impedindo-o de atingir o fotómetro;
- Inicie a aquisição dos dados no “Science Workshop”;
- Enquanto a luz está bloqueada prima o botão “tare” no sensor de luz para colocar o sensor a
zero;
- Comece a rodar devagar o sensor de luz até que o suporte bata no indicador de ângulo fixo à
mesa do espectrómetro.
- Pressione o botão “tare” do sensor de novo;
- Pare a aquisição de dados;
b) Repita este procedimento para outras 2 temperaturas do filamento.
c) Seleccione uma das temperaturas anteriores e registe de novo o respectivo espectro de emissão.
Coloque amostras várias em frente da lâmpada e registe, para cada caso o respectivo espectro de
absorção.
Análise dos dados
Trace os espectros obtidos convertendo a posição angular em comprimento de onda. Determine para
cada caso, a temperatura a que se encontava o filamento e o λ para o qual a intensidade da
radiação emitida é máxima. Verifique a lei de deslocamento de Wien.
Comente os resultados obtidos.
Bibliografia:
[1] “Física Quântica de átomos, moléculas, sólidos, núcleos e partículas”, R. Eisberg e R. Resnick.
[2] “Modern Physics”, R. A. Serway, C. J. Moses e C. A. Moyer, 3rd Ed., Brooks/Cole – Thomson
Learning, 2005.
[3] http://hyperphysics.phy-astr.gsu.edu/hbase/bbrc.html
[4] Intruction Manual and Experiment Guide for the PASCO Scientific mod. OS-8542, 01207105A, ver “recursos lectivos” da disciplina Estrutura da Matéria em http://www.fis.uc.pt
[5] Instruction sheet for the PASCO mod. CI-6628, ver “recursos lectivos” da disciplina Estrutura
da Matéria em http://www.fis.uc.pt .
Apêndice
1. Índice de refracção do prisma
nv
1,78
1,77
Data: Data1_B
Model: Cauchy
1,76
Chi^2
R^2
= 1.5713E-6
= 0.99723
1,75
A
B
1.6886 ±0.0009
3
3
13.9x10 ±0.2x10
1,74
n( λ ) = A +
1,73
B
λ2
1,72
1,71
1,70
400
500
600
700
800
900
1000
1100
λ (nm)
Fig. 1 – Variação do índice de refracção do vidro (do
prisma) com o comprimento de onda.
2. Variação da resistividade do tungsténio com a temperatura
Tabela 2 – Resistividade do tungsténio
em função da temperatura.
T
(K)
300
400
500
600
700
800
900
1000
1100
1200
1300
1400
1500
1600
1700
1800
1900
2000
ρ
(µΩ.cm)
5.65
8.06
10.56
13.23
16.09
19.00
21.94
24.93
27.94
30.98
34.08
37.19
40.36
43.55
46.78
50.05
53.35
56.67
T
(K)
2100
2200
2300
2400
2500
2600
2700
2800
2900
3000
3100
3200
3300
3400
3500
3600
ρ
(µΩ.cm)
60.06
63.48
66.91
70.39
73.91
77.49
81.04
84.70
88.33
92.04
95.76
99.54
103.3
107.2
111.1
115.0
25
2
y = 3,61E-07x + 4,69E-03x + 1,00E+00
2
R = 1,00E+00
20
15
ρ/ρo
10
5
0
0
500
1000
1500
2000
2500
3000
3500
T - To (K)
Fig. 2 - Variação de ρ/ρo em função de (T-T0),
com T0 = 300 K
R
= 1 + α (T - T0 ) + β (T - T0 ) 2
R0