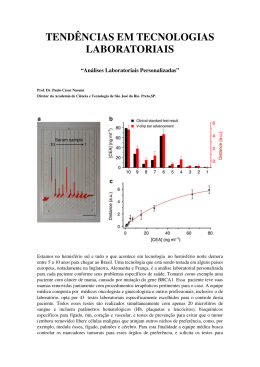
DFis/ICEx/UFMG –Prof. Maurílio Nunes Vieira - Experimentos em Acústica – Projeto PEG 2008/69
Exp 4. Vibração em barras e chapas
1. Objetivos
•
Estudar modos transversais de vibração em barras e chapas;
•
Visualizar os modos com figuras de Chladni e estroboscopia.
2. Introdução
2.1 Vibrações transversais em uma barra
Na estudo de cordas, a rigidez é ignorada e consideram-se apenas as
vibrações transversais, embora outros tipos de vibração possam ocorrer. No
caso de uma barra, a rigidez a deformações longitudinais, transversais ou
torsionais
não é
desprezível,
resultando num
tratamento matemático
relativamente elaborado.
Outro aspecto complicador são as diferentes condições de contorno
de cada extremidade da barra, isto é, presa, livre ou apoiada (Fig. 1).
A
A
P
P
P
L
Fig. 1- Condições de contorno em barras. P = presa, L = livre, A = apoiada.
Neste roteiro, limitaremos ao estudo das vibrações transversais numa barra fixa
em uma extremidade e livre na outra (Fig. 2). Detalhes dos desenvolvimentos
são dados em Kinsler et al. (1982) ou Fletcher e Rossing (1991).
y
x
Fig. 2- Vibração transversal em uma barra
presa em uma extremidade e livre na outra
O estudo do deslocamento transversal y da barra da figura 2 resulta em:
4
∂2 y
2 2 ∂ y
=
−
c
κ
,
∂t 2
∂x 4
(1)
DFis/ICEx/UFMG –Prof. Maurílio Nunes Vieira - Experimentos em Acústica – Projeto PEG 2008/69
onde c =
Y
ρ é a velocidade de fase (sendo Y o módulo de Young do
material1 e ρ é a densidade volumétrica de massa) e κ = d / 12 é o raio de
giração2 de uma barra de seção retangular e espessura d .
A solução desta equação 1 é elaborada e pode ser expressa como:
ω x/v
y = e jωt ( Ae
+ Be
− (ω
x / v)
+ Ce
jω x / v
+ De
−(
jω x / v )
),
(2)
onde v = ω κ é a velocidade de propagação de uma onda de freqüência
angular ω . Note que ondas transversais de freqüências diferentes propagamse com velocidades diferentes, ou seja, a barra é um meio dispersivo para
essas ondas e deformará a forma dos pulsos à medida que eles propagam.
Se a barra da figura 2 tiver comprimento L , a parte real da equação
2 pode ser desenvolvida em:
 

 ωx 
 ωx  
 ωx 
 ωx   
y = cos(ωt + φ )  A cosh  − cos   + B sinh  − sin    ,
 v 
 v 
 v 
 v  

 
(3)
onde as constantes A e B são calculadas a partir das condições iniciais. As
condições de contorno impõem modos de vibração nas seguintes freqüências
apenas:
f =
πcκ
2
8L
(1.194 2 , 2.9882 , 52 , 7 2 ,...) .
(4a)
Estas freqüências são anarmônicas, isto é, o espaçamento entre os termos da
série não é uniforme.
Para o caso de barras livres nas duas extremidades, que é um modelo
para o diapasão, as freqüências permitidas são:
f =
πcκ
2
8L
(3.0112 2 , 52 , 7 2 , 9 2...) .
(4b)
1
O módulo de Young caracteriza a elasticidade do material na seguinte forma da lei
de Hooke: f / S = −Y ⋅ ∂ξ / ∂x , onde f é a força aplicada perpendicularmente à seção
transversal S e ∂ξ / ∂x representa o respectivo alongamento.
2
Se J é o momento de inércia de uma superfície em relação a um eixo, respectivo o
raio de giração é J / S .
Exp 4 - Vibração em barras e chapas
2/7
DFis/ICEx/UFMG –Prof. Maurílio Nunes Vieira - Experimentos em Acústica – Projeto PEG 2008/69
2.2 Vibrações em chapas
Membranas e chapas podem ser vistas como casos bidimensionais de cordas
e barras, respectivamente. Uma superfície pode ser tratada como uma
membrana se ela apresentar rigidez desprezível às deformações. No seu
movimento, a membrana tensa retorna à posição de equilíbrio somente com
a força da tensão superficial à qual ela é submetida. No caso de uma chapa
submetida a alguma deformação, torna-se relevante os valores de rigidez
exercidos pelo material a esforços transversais, longitudinais e de torsão.
As condições de contorno de membranas e chapas são similares às de
cordas e barras. Neste experimento, estudaremos apenas as vibrações em
uma chapa circular com as bordas livres. O tratamento matemático é
complexo e nos limitaremos a apresentar alguns resultados. Veja detalhes em
Fletcher e Rossing (1991).
A equação que descreve a vibração de uma chapa circular fina, em
coordenadas polares (r = raio, θ = ângulo), é:
y mn (r ,θ , t ) = {[ AJ m (k mn r ) + BI m (k mn r ) ] cos(mθ + γ mn )}cos(ω mn t + φ mn ) ,
(5)
onde o termo à direta, fora das chaves, representa a variação temporal do
movimento. Na parte interna das chaves, que representa a “estrutura
espacial” desta vibração, as constantes A e B dependem das condições
iniciais e de contorno, J e I são funções de Bessel ordinárias e hiperbólicas,
respectivamente, k é o número de onda e os índices (m,n) indicam o modo de
vibração da chapa.
Cada condição de contorno impõe possíveis modos de vibração. Estes
modos são designados por kmn, onde m é o número de diâmetros nodais (isto é,
diâmetros que não se movimentam no padrão de onda estacionária) e n é o
número de círculos nodais. A figura 3 ilustra os padrões nodais para uma
chapa circular com extremidade livre (a) ou presa (b).
O cálculo das freqüências de vibração da chapa circular leva aos
valores das tabelas 1, 2 e 3. Nas tabelas, há expressões para os respectivos
modos fundamentais onde c L é a velocidade das ondas longitudinais numa
chapa infinita (detalhes em Fletcher e Rossing, 1991, p. 71), h é a espessura da
Exp 4 - Vibração em barras e chapas
3/7
DFis/ICEx/UFMG –Prof. Maurílio Nunes Vieira - Experimentos em Acústica – Projeto PEG 2008/69
chapa e a o seu raio. Note que, em nenhum caso, as freqüências são múltiplas
inteiras da fundamental.
Fig. 3 - Modos Vibracionais das placas
circulares: (a) extremidade livre e (b)
extremidade presa. O número de modo
(m,n) representado nas figuras fornece o
número de linhas diametrais e o número
de círculos nodais, respectivamente.
Fonte: Fletcher e Rossing (1991, p. 74).
Extremidade livre
Extremidade apoiada
Extremidade fixa
Tab. 1 - Modos vibracionais de chapas circulares. fmn é o modo com m diâmetros nodais
e n círculos nodais. O modo fundamental é f20.(extremidade livre) ou f01.(extremidade
apoiada ou fixa). Veja texto principal para a definição das constantes das expressões
dos modos fundamentais. Fonte: Fletcher e Rossing (1991, p. 73).
Exp 4 - Vibração em barras e chapas
4/7
DFis/ICEx/UFMG –Prof. Maurílio Nunes Vieira - Experimentos em Acústica – Projeto PEG 2008/69
3. Exercícios
1. Verifique que a equação 2 é solução da equação de ondas
transversais em barras.
2. Faça uma tabela relacionando, para uma barra semi-presa, a
freqüência, a velocidade de fase ( v ) e o comprimento de onda
λ = v / f . Expresse os valores em função do valor do 1º. modo normal.
3. Ao contrário do que ocorre na vibração de cordas tensas, os modos
normais de uma barra ou de uma chapa não são uma série harmônica.
Investigue sobre a relevância disto na construção de instrumentos
musicais.
4. Bibliografia
1. LE Kinsler, AF Frey, AB Coppens, JV Sanders, Fundamentals of Acoustics
(3rd. Ed.) - Wiley, New York (1982) – Cap 2
2. NH Fletcher, TD Rossing, The Physics of Musical Instruments – SpringerVerlag, New York (1991) – Cap 2 e 3
3. Relatórios dos estudantes Mainda Silva Araújo (bolsista PEG), Saulo
Araújo do Nascimento (bolsista ProNoturno) e José Eduardo Silva
(Estágio Docente).
4. Transparências usadas no seminário 2.
5. AA Campos, ES Alves e NL Speziali (2007), Física Experimental na
Universidade – Editora UFMG.
Exp 4 - Vibração em barras e chapas
5/7
DFis/ICEx/UFMG –Prof. Maurílio Nunes Vieira - Experimentos em Acústica – Projeto PEG 2008/69
5. Parte Prática
5.1 Material
•
•
•
•
•
Barras Cruzadas
Kit das figuras de Chladni
Gerador de áudio
Vibrador mecânico Pasco
Estroboscópio
5.2 Procedimentos
Figura 4: Montagem para vibração transversal em
barras
Fig. 5 - Montagem para vibração em placas
Observações:
Roteiro sobre barras adaptado de AA Campos (2007, p. 156-157).
Inserir unidades e incertezas das medidas.
Fazer relatório e anexar exercícios.
Exp 4 - Vibração em barras e chapas
6/7
DFis/ICEx/UFMG –Prof. Maurílio Nunes Vieira - Experimentos em Acústica – Projeto PEG 2008/69
1. Barras. Trave o eixo do vibrador, remova o fio e encaixe o conjunto de
lâminas metálicas como mostrado na figura 4. Destrave o eixo do
vibrador.
2. Varie, no gerador de áudio, a freqüência de vibração, enquanto
observa as lâminas metálicas. Determine as freqüências de ressonância
até o 4° modo (≈ 255 Hz). Meça também a posição dos nós de vibração
da barra. Tente visualizar o movimento com o auxílio do estroboscópio.
3. Faça uma tabela e um esboço das formas das ondas estacionárias que
são observadas para cada uma das freqüências de ressonância de
cada lâmina. Determine, para a lâmina de maior comprimento, as
razões fn/f1 entre as freqüências de ressonância de cada modo e a do
modo fundamental f1 . Indique também a posição dos nós. Compare
com os valores teóricos abaixo (L = comprimento da barra).
Freqüência
f1
nós
0
6,267 f1
0 0,783L
17,55 f1
0 0,504 L 0,868 L
34,39 f1
0 0,358 L 0,654 L 0,906 L
4. Chapas. Use o kit das figuras de Chladni para montar o experimento da
figura 5.
5. Faça uma tabela com um esboço das formas das ondas estacionárias
que são observadas na placa e as freqüências. Tente visualizar o
movimento com o auxílio do estroboscópio.
6. Determine as razões fn/f1 entre as freqüências de cada modo (até o 4°
ou 5° modo) e a do modo fundamental f1 . Compare com os valores
apresentados na tabela 1 da introdução.
Exp 4 - Vibração em barras e chapas
7/7